- Δύο μπάλες Α και Β κινούνται με διαφορετικές ταχύτητες με μέτρα υΑ και υΒ αντίστοιχα, στην επιφάνεια ενός λείου οριζόντιου τραπεζιού και εκτοξεύονται την ίδια χρονική στιγμή από την άκρη του.
Αν υΑ > υΒ, τότε- οι σφαίρες Α και Β θα φθάσουν ταυτόχρονα στο έδαφος.
- η σφαίρα Α θα φτάσει πρώτη στο έδαφος.
- η σφαίρα Β θα φτάσει πρώτη στο έδαφος.
- τα στοιχεία δεν επαρκούν να συμπεράνουμε πώς θα φτάσουν οι σφαίρες στο έδαφος.
- Μικρή σφαίρα (Κ) αφήνεται να πέσει από μικρό ύψος h, εκτελώντας ελεύθερη πτώση. Μια ίδια σφαίρα (Λ) βάλλεται από το ίδιο ύψος με οριζόντια ταχύτητα μέτρου υ0.
Εάν υΚ και υΛ είναι τα μέτρα των ταχυτήτων των δύο σφαιρών τη χρονική στιγμή που φτάνουν στο έδαφος, τότε- υΚ = υΛ.
- υΚ > υΛ.
- υΚ < υΛ.
- τα στοιχεία δεν επαρκούν να συμπεράνουμε πώς θα φτάσουν οι σφαίρες στο έδαφος.
- Από αεροπλάνο που πετάει με σταθερή ταχύτητα υ σε ύψος Η, αφήνεται να πέσει ένα κιβώτιο. Ο πιλότος του αεροπλάνου βλέπει ότι η τροχιά του κιβωτίου είναι
- ευθύγραμμη και οριζόντια.
- ευθύγραμμη προς τα κάτω.
- παραβολική.
- κυκλική.
- Δύο σφαίρες Σ1 και Σ2 εκτοξεύονται οριζόντια με την ίδια ταχύτητα από σημεία Α και Β αντίστοιχα που βρίσκονται στην ίδια κατακόρυφο και σε ύψη από το έδαφος h1 και h2 αντίστοιχα, για τα οποία ισχύει h1 = 4h2.
Αν η οριζόντια μετατόπιση από το σημείο εκτόξευσης των σφαιρών Σ1 και Σ2 μέχρι το σημείο πρόσκρουσης στο έδαφος (δηλαδή το βεληνεκές), είναι x1 και x2 αντίστοιχα, τότε- x1 = 4x2.
- x1 = √2x2.
- x1 = 2x2.
- x2 = 4x1.
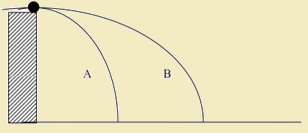
Η σφαίρα του σχήματος εκτοξεύεται δύο φορές με διαφορετικές αρχικές ταχύτητες εκτελώντας οριζόντια βολή, από το ίδιο ύψος h από το έδαφος. Στο σχήμα φαίνεται η τροχιά που ακολουθεί μετά την πρώτη ρίψη (Α) και μετά τη δεύτερη ρίψη (Β), αντίστοιχα. Ο χρόνος που θα κινηθεί η σφαίρα μέχρι να φτάσει στο έδαφος- δεν μπορεί να προσδιοριστεί, γιατί τα στοιχεία δεν επαρκούν.
- είναι μεγαλύτερος στην τροχιά Α.
- είναι μεγαλύτερος στην τροχιά Β.
- είναι ίδιος για τις τροχιές Α και Β.
- Δύο παιδιά, η Μαρία κι η Γεωργία, παίζουν στην ακροθαλασσιά πετώντας πέτρες. Κάποια στιγμή τα δύο παιδιά πετούν ταυτόχρονα, από το ίδιο ύψος, από μία πέτρα με οριζόντια ταχύτητα υΜ και υΓ, αντίστοιχα. Για τα μέτρα των ταχυτήτων ισχύει υΜ > υΓ. Κατά την κίνηση των πετρών, τη χρονική στιγμή t, η πέτρα της Μαρίας και αυτή της Γεωργίας βρίσκονται σε ύψη hΜ και hΓ, αντίστοιχα από το έδαφος.
Για τα ύψη hΜ και hΓ κάθε χρονική στιγμή ισχύει- hΜ < hΓ.
- hΜ = hΓ.
- hΜ > hΓ.
- hΜ = hΓ/2.
- Μικρή σφαίρα αφήνεται να πέσει από μικρό ύψος h, εκτελώντας ελεύθερη πτώση. Μια ίδια σφαίρα βάλλεται από το ίδιο ύψος με οριζόντια ταχύτητα μέτρου υ0.
Έστω t1 και t2 οι χρόνοι που κάνουν η πρώτη και η δεύτερη σφαίρα αντίστοιχα, για να φτάσουν στο έδαφος. Τότε ισχύει:- t1 = t2.
- t1 = t2/2.
- t1 > t2.
- t1 < t2.
- Δύο αεροπλάνα (1) και (2) κινούνται με ταχύτητες οριζόντιας διεύθυνσης, σε ύψη H1 = H και H2 = 4H αντίστοιχα, πάνω από το έδαφος.
Κάποια χρονική στιγμή t0 = 0, αφήνεται να πέσει από κάθε αεροπλάνο ένα δέμα. Τα δέματα φτάνουν στο έδαφος τις χρονικές στιγμές t1 και t2, όπου η χρονική στιγμή t1 αντιστοιχεί στο δέμα που έπεσε από το αεροπλάνο (1), ενώ η χρονική στιγμή t2 αντιστοιχεί στο δέμα που έπεσε από το αεροπλάνο (2).
Τότε, ο λόγος t2 / t1 είναι ίσος με- 1.
- 2.
- 1/2.
- 1/4.
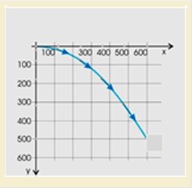
Μία σφαίρα εκτελεί οριζόντια βολή με αρχική οριζόντια ταχύτητα υ0. Στο παραπάνω σχήμα φαίνονται οι συντεταγμένες της θέσης της σφαίρας μετρημένες σε m. Από το σχήμα συμπεραίνουμε ότι- υ0 = 50 m/s.
- υ0 = 60 m/s.
- υ0 = 100 m/s.
- υ0 = 600 m/s.
- Από σημείο Ο που βρίσκεται σε ύψος Η πάνω από το έδαφος βάλλεται οριζόντια ένα σώμα με αρχική ταχύτητα μέτρου υ0.
Τη στιγμή που το μέτρο της κατακόρυφης συνιστώσας της ταχύτητας έχει γίνει ίσο με το μέτρο της οριζόντιας συνιστώσας της ταχύτητας, το σώμα έχει μετατοπιστεί οριζόντια κατά x και κατακόρυφα κατά y. Ο λόγος των μετατοπίσεων x/y του σώματος εκείνη τη στιγμή είναι ίσος με- 1/2.
- 1.
- 2.
- 4.
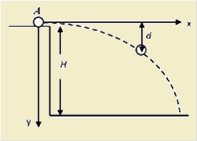
Ένα σφαιρίδιο εκτοξεύεται από σημείο Α που βρίσκεται σε ύψος H από το έδαφος, με αποτέλεσμα να εκτελέσει οριζόντια βολή. Η κινητική ενέργεια του σφαιριδίου αμέσως μετά την εκτόξευση του είναι Κ0. Θεωρήστε ως d την κατακόρυφη απόσταση του σφαιριδίου κάθε χρονική στιγμή από το επίπεδο εκτόξευσης.
Ποιο από τα παρακάτω διαγράμματα παριστάνει σωστά τη μεταβολή της κινητικής ενέργειας Κ του σώματος σε συνάρτηση με την απόσταση d;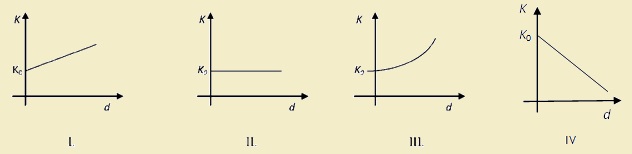
- Η (Ι).
- Η (ΙΙ).
- Η (ΙΙΙ).
- Η (ΙV).
- Από αεροπλάνο που πετάει με σταθερή ταχύτητα υ σε ύψος Η, αφήνεται να πέσει ένα δέμα. Ακίνητος παρατηρητής που βρίσκεται στο έδαφος βλέπει ότι η τροχιά του δέματος είναι
- ευθύγραμμη και οριζόντια.
- ευθύγραμμη προς τα κάτω.
- παραβολική.
- κυκλική.
- Από σημείο Ο που βρίσκεται σε ύψος Η πάνω από το έδαφος βάλλεται οριζόντια ένα σώμα μάζας m με αρχική ταχύτητα μέτρου υ0, έχοντας κινητική ενέργεια Κ0.
Τη στιγμή που η κινητική ενέργεια του σώματος έχει διπλασιαστεί, το μέτρο της κατακόρυφης συνιστώσας της ταχύτητας είναι υy και της οριζόντιας συνιστώσας υx.
Ο λόγος των μέτρων των ταχυτήτων υx / υy του σώματος εκείνη τη στιγμή είναι ίσος με- 1.
- 2.
- 1/2.
- 1/4.
- Από σημείο Ο, που βρίσκεται σε ύψος Η πάνω από το έδαφος, βάλλεται οριζόντια ένα σώμα με αρχική ταχύτητα μέτρου υ0. Κατά τη στιγμή της εκτόξευσης η κινητική ενέργεια του σώματος K είναι ίση με τη βαρυτική δυναμική του ενέργεια U. Θεωρήστε ως επίπεδο αναφοράς για τη βαρυτική δυναμική ενέργεια το έδαφος.
Τότε, η μέγιστη οριζόντια μετατόπιση του σώματος x τη στιγμή που φτάνει στο έδαφος (βεληνεκές) και το αρχικό ύψος Η θα συνδέονται με τη σχέση- x = H.
- x = 2H.
- x = 4H.
- H = 2x.
- Από καθορισμένο ύψος Η πάνω από οριζόντιο δάπεδο και σε συγκεκριμένο τόπο, πετάμε μια μικρή σφαίρα με οριζόντια αρχική ταχύτητα υ0. Η τελική ταχύτητα της σφαίρας όταν φτάνει στο δάπεδο σχηματίζει με την οριζόντια διεύθυνση γωνία φ, η οποία είναι
- ίση με 450.
- ανεξάρτητη από το χρόνο που χρειάστηκε να φτάσει στο έδαφος.
- ανεξάρτητη από το μέτρο υ0 της αρχικής ταχύτητας.
- εξαρτώμενη από το μέτρο υ0 της αρχικής ταχύτητας.
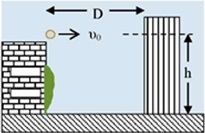
Μικρή σφαίρα βάλλεται οριζόντια με ταχύτητα μέτρου υ0 = 10 m/s από την ταράτσα ενός κτιρίου και από ύψος h = 45 m από το έδαφος που θεωρείται οριζόντιο. Σε απόσταση D = 20 m από το κτίριο αυτό υπάρχει δεύτερο ψηλό κτίριο όπως φαίνεται και στο σχήμα. Ο χρόνος κίνησης μέχρι την πρώτη πρόσκρουση του σώματος οπουδήποτε (δηλαδή, είτε στο έδαφος είτε στο απέναντι κτήριο) είναι- 0,5 s.
- 1 s.
- 2 s.
- 3 s.
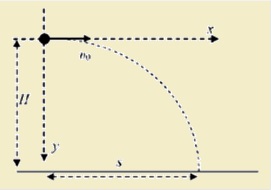
Τα διαγράμματα που ακολουθούν αναφέρονται στην περίπτωση μιας οριζόντιας βολής στη Σελήνη που γίνεται από ύψος H και αφορούν τις συνιστώσες της ταχύτητας κατά μήκος των αξόνων χ και y. Θεωρούμε ότι το σώμα που εκτελεί την οριζόντια βολή, ακινητοποιείται στιγμιαία μόλις φτάνει στο σεληνιακό έδαφος, όπως φαίνεται και από τα διαγράμματα.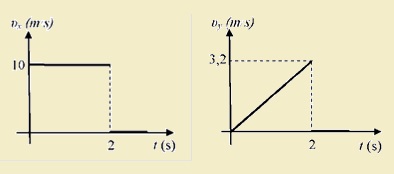
Οι τιμές της επιτάχυνσης της βαρύτητας στην επιφάνεια της Σελήνης, του ύψους H και της οριζόντιας απόστασης s στην οποία το σώμα χτυπά στο έδαφος είναι αντιστοίχως,- 10 m/s2, 10 m, 2 m.
- 1,6 m/s2, 2 m, 10 m.
- 1,6 m/s2, 10 m, 2 m.
- 1,6 m/s2, 3,2 m, 20 m.
- Δύο μικρές σφαίρες A και Β εκτοξεύονται ταυτόχρονα τη χρονική στιγμή t = 0 s οριζόντια από ύψη hA, hB αντίστοιχα, που βρίσκονται στην ίδια κατακόρυφο. Οι αρχικές οριζόντιες ταχύτητες των δύο σφαιρών συνδέονται με τη σχέση: υA = 3υB.
Αν τα σώματα φθάνοντας στο έδαφος προσκρούουν στην ίδια οριζόντια απόσταση από την κοινή κατακόρυφο (ίδιο βεληνεκές), τότε τα ύψη hA, hB συνδέονται με τη σχέση- hA / hB = 1/3.
- hA / hB = 4/9.
- hA / hB = 1/9.
- hA / hB = 3.
- Ένα αεροπλάνο κινείται οριζόντια σε ύψος h πάνω από το έδαφος με σταθερή ταχύτητα υ0. Κάποια χρονική στιγμή αφήνεται να πέσει από το αεροπλάνο ένα δέμα. Το δέμα φτάνει στο έδαφος μετά από χρόνο t = 4 s.
Το αεροπλάνο εξακολουθώντας την οριζόντια κίνησή του στο ίδιο ύψος h, αυξάνει την ταχύτητά του σε 2υ0 και στη συνέχεια κινείται με αυτή την ταχύτητα. Κάποια χρονική στιγμή αφήνεται να πέσει από το αεροπλάνο ένα δεύτερο δέμα. Το δεύτερο δέμα φτάνει στο έδαφος μετά από χρόνο- t1 = 0,5 s.
- t1 = 2 s.
- t1 = 4 s.
- t1 = 8 s.
- Μαθητής βρίσκεται στην ταράτσα μιας πολυκατοικίας και κρατάει στο δεξί του χέρι ένα μπαλάκι κόκκινου χρώματος και στο αριστερό του ένα όμοιο πράσινου χρώματος. Εκτοξεύει ταυτόχρονα από το ίδιο ύψος και οριζόντια τα δύο μπαλάκια, το πράσινο με διπλάσια ταχύτητα από το κόκκινο. Τότε,
- και τα δύο μπαλάκια φτάνουν ταυτόχρονα.
- φτάνει πρώτα το πράσινο μπαλάκι.
- φτάνει πρώτα το κόκκινο μπαλάκι.
- δεν μπορούμε να συμπεράνουμε ποιο μπαλάκι φτάνει πρώτο, γιατί τα στοιχεία δεν επαρκούν.
- Δύο όμοιες σφαίρες 1 και 2 εκτοξεύονται οριζόντια από την επιφάνεια τραπεζιού με αρχικές ταχύτητες υ1 = υ0 και υ2 = 2υ0, αντίστοιχα. Η σφαίρα 1 φθάνει στο έδαφος ύστερα από χρονικό διάστημα t1 και σε οριζόντια απόσταση από το σημείο βολής x1. Η σφαίρα 2 φθάνει στο έδαφος ύστερα από χρονικό διάστημα t2 και σε οριζόντια απόσταση από το σημείο βολής x2. Από αυτά συμπεραίνουμε ότι
- t2 > t1.
- t2 < t1.
- x2 < x1.
- x2 > x1.
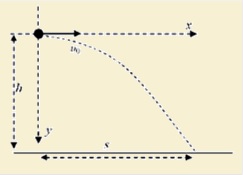
Ένα σώμα εκτοξεύεται από ύψος h με οριζόντια ταχύτητα μέτρου υ0 =√2gh
.
Η οριζόντια απόσταση x του σημείου που θα χτυπήσει στο έδαφος από το σημείο εκτόξευσης (βεληνεκές), θα είναι- x = h.
- x = 2h.
- x =√2h.
- x = h/2.
- Μία μικρή σφαίρα εκτοξεύεται οριζόντια με ταχύτητα υ0 από ύψος h. Το μέτρο της ταχύτητάς της όταν φτάνει στο έδαφος είναι ίσο με 2υ0.
Το ύψος h από το οποίο εκτοξεύτηκε η σφαίρα δίδεται από τη σχέση- h = (υ0)2 / 2g.
- h = 2(υ0)2 / 3g.
- h = 3(υ0)2 / 2g.
- h = υ0 / 2g.
- Μικρή σφαίρα εκτοξεύεται την χρονική στιγμή t = 0 s οριζόντια με ταχύτητα υ0 από ύψος H από το έδαφος. Τη χρονική στιγμή t = t1 η σφαίρα απέχει h = 15H/16 από το έδαφος.
Εάν x είναι η συνολική οριζόντια απόσταση (βεληνεκές) που θα διανύσει η σφαίρα μέχρι να φτάσει στο έδαφος και x1 η οριζόντια απόσταση που έχει διανύσει η σφαίρα μέχρι τη χρονική στιγμή t1, τότε ισχύει:- x1 = x/2.
- x1 = x/4.
- x = x1/2.
- x = x1/4.
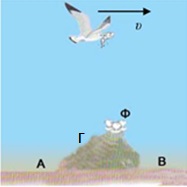
Ένα ψαροπούλι πετά οριζόντια με ταχύτητα υ κρατώντας στο ράμφος του ένα ψάρι. Τη χρονική στιγμή t που βρίσκεται πάνω από το βράχο, στην ίδια κατακόρυφη με τη φωλιά Φ των μικρών του, αφήνει το ψάρι να πέσει. Τότε,- το ψάρι θα πέσει στο σημείο Α του εδάφους.
- το ψάρι θα πέσει μέσα στη φωλιά Φ.
- το ψάρι θα πέσει στο σημείο Β του εδάφους.
- το ψάρι θα πέσει στο σημείο Γ του εδάφους.