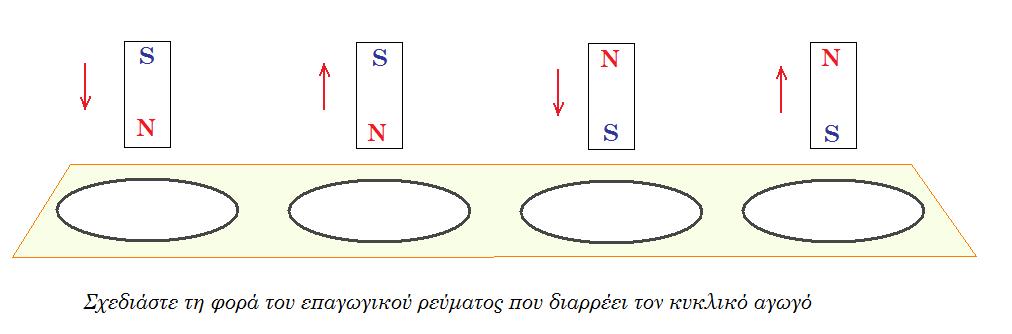
ΓΡΑΠΤΗ ΔΟΚΙΜΑΣΙΑ ηλεκτρομαγνητισμός - επαγωγή - εναλλασσόμενο ρεύμα

ονοματεπώνυμο :                                                                            ημερομηνία :

Α1.

Α2.

Β2    α = 3g/2  κατακόρυφη προς τα κάτω

ΘΕΜΑ 1ο

Δίνεται το κύκλωμα του σχήματος, το οποίο αποτελείται από  ηλεκτρική πηγή με ΗΕΔ  Ε = 24 V  και εσωτερική αντίσταση  r = 2 Ω
 κυκλικό αγωγό ακτίνας  ρ = 2π cm   και  ωμικής αντίστασης  Rκ = 6 Ω
 σωληνοειδές με Ν=1.000 σπείρες, μήκος L = 20 cm, αντίσταση μιας σπείρας   R* = 0,003 Ω / σπείρα, αντίσταση  R = 2 Ω,   τρεις διακόπτες,  μεταλλικούς αγωγούς (σύρματα) αμελητέας ωμικής αντίστασης. 
Αρχικά και οι τρεις διακόπτες είναι ανοικτοί.
α.   Κλείνουμε το διακόπτη (δ₁). Να υπολογίσετε την ένταση του μαγνητικού πεδίου (μέτρο και κατεύθυνση) στο κέντρο του κυκλικού ρευματοφόρου αγωγού.
β.   Κλείνουμε και το διακόπτη (δ₂). Να υπολογίσετε
     β1.   το μέτρο της έντασης του μαγνητικού πεδίου στο κέντρο του κυκλικού ρευματοφόρου αγωγού.
     β2.   το μέτρο της έντασης του μαγνητικού πεδίου στο κέντρο του σωληνοειδούς
γ.   Κλείνουμε και το διακόπτη (δ₃). Να υπολογίσετε
    γ1.  το μέτρο της έντασης του μαγνητικού πεδίου στο κέντρο του κυκλικού ρευματοφόρου αγωγού.
    γ2.  το μέτρο της έντασης του μαγνητικού πεδίου στο άκρο του σωληνοειδούς.
Δίνεται η σταθερά   k_μ  =  10^-7 Ν / Α² . 

E = 24 V      r = 2 Ω      R_κ = 6 Ω
i = E / (r + R_κ) = 24 V / (2+6) Ω => i = 3 A
B_κ = 10^-7 . 2π . i / ρ = 10^-7 . 2π . 3 / 2π.10^-2 => Bκ = 3.10^-5 T

R_πην = 1000 . R* = 1000 . 0,003 Ω = 3 Ω
R_κ,πην = R_κ . R_πην / (R_κ + R_πην) = 6 . 3 / 9 = 2 Ω
i = E / (r + R_κ,πην) = 24 V / (2+2) Ω => i = 6 A          V_πολική = Ε - i. r = 24 - 6 . 2 = 12 V    
  i_κ = 12 V / 6 Ω = 2 Α         B_κ = 10^-7 . 2π . i / ρ = 10^-7 . 2π . 2 / 2π.10^-2 => B_κ = 2.10^-5 T
  i_πην = 12 V / 3 Ω = 4 Α     B_πην = 4π.10^-7 . Ν.i / l = 4π.10^-7 . 1000 . 4 / 0,2 => B_πην = 8.π.10^-3 Τ

1 / R_ολ = 1/R_κ + 1/R_πην + 1/R = 1/6 + 1/3 + 1/2 = 1+2+3 / 6 = 1 => R_ολ = 1 Ω
i = E / (r + R_ολ) = 24 V / (2+1) Ω => i = 8 A              V_πολική = Ε - i. r = 24 - 8 . 1 = 16 V    

  i_κ = 16 V / 6 Ω = 8/3 Α      B_κ = 10^-7 . 2π . i / ρ = 10^-7 . 2π . (8/3) / 2π.10^-2 => B_κ = 8/3 . 10^-5 T
  i_πην = 16 V / 3 Ω = 16/3 Α      B_πην =  ½ . 4π.10^-7 . Ν.i / l = ½ . 4π.10^-7 . 1000 . (16/3) / 0,2 => B_πην = 16.π/3 . 10^-3 Τ

ΘΕΜΑ 2ο

Ένας αντιστάτης αντίστασης  R = 200 Ω  τροφοδοτείται από εναλλασσόμενη τάση  V = V₀ ημωt.  Στο σχήμα φαίνεται η γραφική παράσταση της στιγμιαίας ισχύος στον αντιστάτη σε συνάρτηση με το χρόνο.
2α)   Να βρείτε την περίοδο, τη συχνότητα και το πλάτος της εναλλασσόμενης τάσης.
2β)   Υπολογίστε τη θερμότητα που εκλύεται στον αντιστάτη σε χρόνο ίσο με αυτόν που χρειάζεται η τάση για να ολοκληρώσει 500 πλήρεις εναλλαγές.
2γ)   Ποια χρονική στιγμή η στιγμιαία ισχύς του εναλλασσόμενου ρεύματος ισούται με τη μέση ισχύ για πρώτη φορά;
2δ)   Αντικαθιστούμε τον αντιστάτη με δύο άλλους αντίστασης 100 Ω  ο καθένας, τους οποίους συνδέουμε παράλληλα μεταξύ τους και στη συνέχεια στα άκρα του συστήματός τους εφαρμόζουμε την ίδια εναλλασσόμενη τάση. Να βρείτε πόσο τοις εκατό (%) μεταβάλλεται η μέση ισχύς στο κύκλωμα.

                                          α)  0,02 s   50 Hz   200 V   β)  1000 J    γ)   1/400 s   δ)  300 %

ΘΕΜΑ 3ο

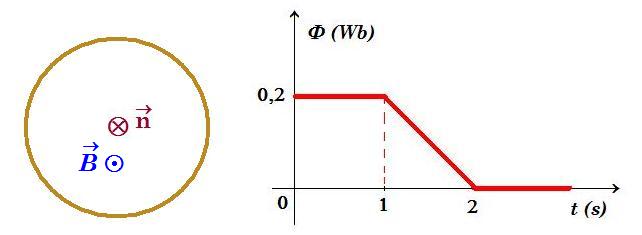
Ένα συρμάτινο πλαίσιο σχήματος τετραγώνου πλευράς  α = 0,1 m, αμελητέας αντίστασης, έχει  Ν=100 σπείρες και στρέφεται μέσα σε ομογενές μαγνητικό πεδίο έντασης Β, με γωνιακή ταχύτητα ω   γύρω από άξονα που περνά από τα μέσα δύο απέναντι πλευρών του πλαισίου και είναι κάθετος στις δυναμικές γραμμές του πεδίου. Στο σχήμα παριστάνεται η μαγνητική ροή που διέρχεται από κάθε σπείρα του πλαισίου σε συνάρτηση με το χρόνο.
3α)  Να βρείτε την ένταση Β του μαγνητικού πεδίου.
3β)  Να γράψετε τη χρονική εξίσωση της εναλλασσόμενης τάσης που δημιουργείται στα άκρα του πλαισίου.
3γ)  Να βρείτε για πόσο χρονικό διάστημα σε κάθε περίοδο η αλγεβρική τιμή της στιγμιαίας τάσης είναι μεγαλύτερη ή ίση από την ενεργό τάση.
3δ)  Συνδέουμε τα άκρα του πλαισίου με αντιστάτη αντίστασης  R = 10 Ω.  Να βρείτε τη θερμότητα που εκλύεται στον αντιστάτη, στο χρονικό διάστημα μέσα στο οποίο το πλαίσιο εκτελεί 20 στροφές.

Φ(t) = 0,02/π . ημ(10πt + π/2)  =  0,02/π . συν(10πt)                          ω = 2π/Τ = 2π/0,2 = 10π rad/s

Φ = Β . Α  =>  0,02/π = Β . 0,01   =>   B = 2/π Tesla

E_επ = - ΔΦ/Δt . N  =  - 10π . 0,02/π . συν(10πt + π/2) . 100 =  - 20 . συν(10πt + π/2)  =>  V(t) =  20 . ημ(10πt)   

V(t)  >  V_εν  =>   20 . ημ(10πt)  >  20 . 0,7   =>  ημ(10πt)  >   0,7 = ημ(π/4)  =>   π/4  <  10πt  <  3π/4  =>  1/40 s <  t  <  3/40 s

i = V / R =  20 . ημ(10πt) / 10 =  2 . ημ(10πt)  (SI)            N = 20    t = 20 . T = 20 . 0,2 = 4 s

Q_θερμ =  Ι_εν² . R . t  =  2² / 2 . 10 . 4  =  80 Joule