

ΘΕΜΑ Γ
Το σώμα (1) μάζας m1 =1Kg συνδέεται με το πάνω άκρο του ιδανικού, κατακόρυφου ,ελατηρίου (1) σταθερής k1=100N/m , το κάτω άκρο του ιδανικού κατακόρυφου ελατηρίου (2) με k2 =100N/m και είναι ακίνητο. Το πάνω άκρο του ελατηρίου (2) συνδέεται με το ακίνητο σώμα (2) μάζας m2=2Kg , το οποίο συνδέεται με το κάτω άκρο του αβαρούς, μη ελαστικού, κατακόρυφου νήματος. Το πάνω άκρο του νήματος συνδέεται με το ταβάνι. Το ελατήριο (1) έχει το φυσικό του μήκος και συνδέεται με σώμα (3) μάζας m3=2Κg το οποίο είναι ακίνητο στο δάπεδο.
Kατεβάζουμε το σώμα (1) κατά d και τα κρατάμε. Τη χρονική στιγμή t=0 το αφήνουμε. Θεωρούμε θετική φορά για τις αλγεβρικές τιμές προς τα κάτω και τα σώματα χωρίς διαστάσεις.
Α. Να βρεθεί η μέγιστη τιμή της απόστασης d για να εκτελεί το σώμα (1) ΑΑΤ και τα σώματα (2), (3) να παραμένουν ακίνητα (5μ)
Β. Αν η απόσταση d είναι η μέγιστη του ερωτήματος Α, να βρεθούν
Β1) Οι εξισώσεις της απομάκρυνσης και της ταχύτητας των σώματος (1) σε συνάρτηση με το χρόνο. (4μ)
Β2) Η αλγεβρική τιμή της δύναμης η οποία ασκείται από το νήμα στο σώμα (2) και της κάθετης αντίδρασης στο σώμα (3) σε συνάρτηση με την απομάκρυνση και σε συνάρτηση
με το χρόνο. Να γίνουν οι αντίστοιχες γραφικές παραστάσεις. (6μ)
Β3) Το ρυθμό μεταβολής της κινητικής ενέργειας του σώματος (1) όταν διέρχεται από τη θέση του φυσικού μήκους του ελατηρίου (2) , με φορά προς τα πάνω. (4μ)
Β4) Η απομάκρυνση του σώματος (1) για την οποία η δυναμική ενέργεια του ελατηρίου (1) ισούται με τη δυναμική ενέργεια του ελατηρίου (2). Στη συνέχεια σε κοινούς άξονες U-x να γίνουν οι γραφικές παραστάσεις των δυναμικών ενεργειών των ελατηρίων σε συνάρτηση με την απομάκρυνση. (6μ)
 ισορροπία (1) : m1 g = Fελατ,2 = k2 Δl2 => 10 = 100 Δl2 => Δl2 = 0,1 m το ελατήριο (2) είναι επιμηκυμένο στη Θ.Ι.
ισορροπία (1) : m1 g = Fελατ,2 = k2 Δl2 => 10 = 100 Δl2 => Δl2 = 0,1 m το ελατήριο (2) είναι επιμηκυμένο στη Θ.Ι.
ισορροπία (2) : m2 g + Fελατ,2 = Τ => m2 g + m1 g = Τ => Τ = 30 Ν
σώμα (1) : ΣF(1) = - k1 x - k2 (x + Δl2) + m1 g = - k1 x - k2 x - k2 Δl2 + m1 g = - k1 x - k2 x = - (k1 + k2) x
D = k1 + k2 = 200 N/m ω = √(D/m1) = 10√2 rad/s x = d ημ(ωt + π/2)
ακινησία σώματος (2) : m2 g + Fελατ,2 = Τ => m2 g - k2 (x + Δl2) = Τ ³ 0 => 20 - 100 ( x - 0,1 ) = Τ ³ 0 =>
=> 20 - 100 x + 10 ³ 0 => x £ 0,3 m
ακινησία σώματος (3) : m3 g + Fελατ,1 = N => m2 g - k1 x = N ³ 0 => 20 ³ 100 x => x £ 0,2 m
τότε xmax = 0,2 m = d μέγιστο πλάτος ταλάντωσης
x(t) = 0,2 ημ(10√2t + π/2) v(t) = 2√2 συν(10√2t + π/2) α(t) = - 40 ημ(10√2t + π/2)
Τ = m2 g - k2 (x + Δl2) => Τ = 20 - 100 (x + 0,1) => Τ(x) = 10 - 100 x ή Τ(t) = 10 - 20 ημ(10√2t + π/2)
Ν = m2 g - k1 x => Ν(x) = 20 - 100 x ή Ν(t) = 20 - 20 ημ(10√2t + π/2)
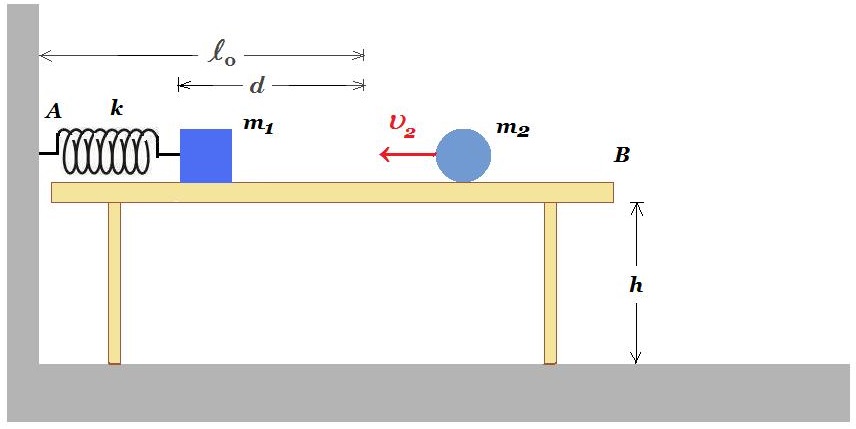
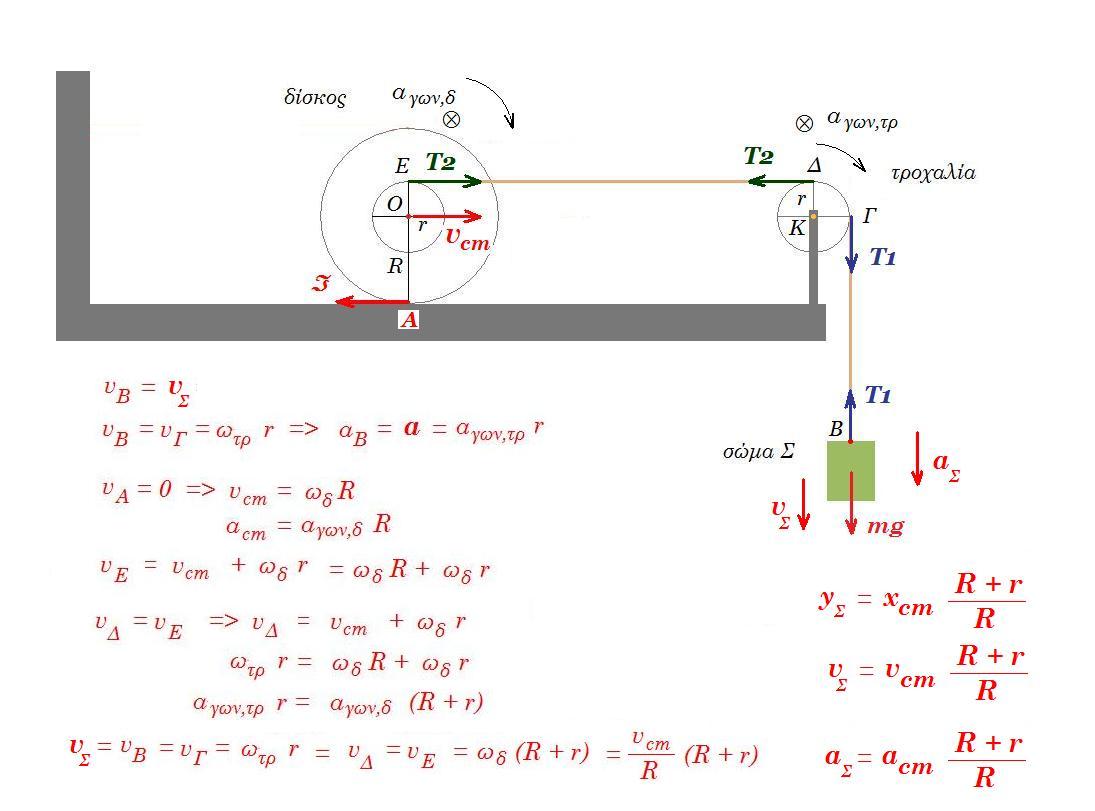
Θέμα 1. κρούση - κεντρομόλος επιτάχυνση
Σώμα Σ1 μάζας m1 εκτοξεύεται τη χρονική στιγμή t = 0 από το σημείο Α οριζόντιου δαπέδου, με το οποίο παρουσιάζει συντελεστή τριβής μ = 0,1 με οριζόντια ταχύτητα υ0. Το σώμα Σ1 αφού διανύσει απόσταση s = 18 m συγκρούεται μετωπικά και ελαστικά με άλλο σώμα Σ2 μάζας m2 = 0,3 kg, το οποίο αρχικά ισορροπεί δεμένο στο ένα άκρο κατακόρυφου αβαρούς νήματος μήκους l = 0,6 m, το άλλο άκρο του οποίου είναι στερεωμένο σε ακλόνητο σημείο Ο. Το μέτρο της ταχύτητας του Σ2 αμέσως μετά την κρούση είναι υ2' = 6 m/s. Το σώμα Σ1 μετά την κρούση επιστρέφει και σταματά στην αρχική θέση Α.
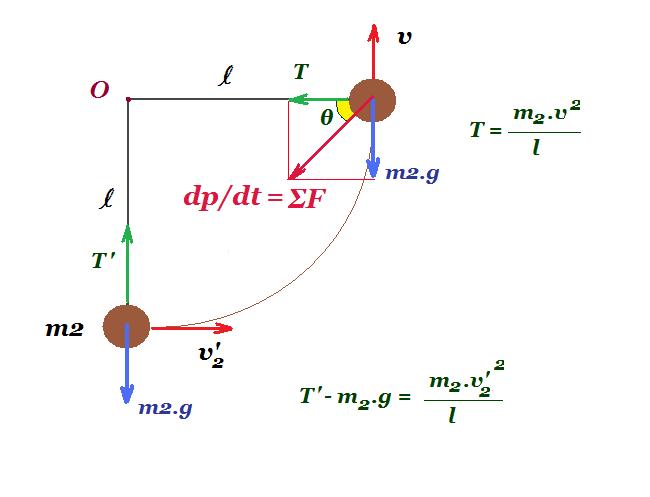
το Σ1 κινείται με επιβράδυνση : α = μ g = 0,1 10 => a = 1 m/s2
η δύναμη τριβής : Τ = μ Ν = μ m1 g = 0,1 m1 10 = m1
αφού διανύσει 18 m θα έχει ταχύτητα v1 = v0 - a t s = v0 t - 0,5 a t2
0,5 m1 v02 = 0,5 m1 v12 + T s => 0,5 m1 v02 = 0,5 m1 v12 + m1 s => v02 = v12 + 2.s => v02 = v12 + 36




Θέμα 7.
Το σώμα Σ μάζας m1 = 2 kg ισορροπεί στο άκρο ελατηρίου επάνω στο κεκλιμένο επίπεδο (θ = 30°). Το ελατήριο έχει επιμήκυνση Δl = 0,05 m. Απομακρύνουμε το σώμα προς τα κάτω επί του κεκλιμένου επιπέδου κατά 0,1 m και το αφήνουμε ελέυθερο να εκτελέσει Α.Α.Τ. Όταν φθάνει στην ανώτερη θέση ταλάντωσης συσσωματώνεται με κινούμενο σώμα μάζας m2 = 4 kg που κινείται οριζόντια με σταθερή ταχύτητα υ0 = √3 m/s. Θετική φορά προς τα δεξιά.
α) Βρείτε την εξίσωση της δύναμης του ελατηρίου συναρτήσει του χρόνου για την Α.Α.Τ. του σώματος Σ1 πριν την κρούση.
β) Βρείτε την απώλεια ενέργειας κατά την κρούση των σωμάτων και την μεταβολή της ορμής για κάθε σώμα κατά την κρούση.
γ) Βρείτε το πλάτος ταλάντωσης του συσσωματώματος. Εκφράστε τον ρυθμό μεταβολής της ταχύτητας του συσσωματώματος συναρτήσει του χρόνου ( dv/dt = a )
k = m1 ω2 => 200 = 2 ω2 => ω = 10 rad/s T = 2π/ω = π/5 s f = 1/T = 5/π Hz
x(t) = 0,1 ημ(10t + 3π/2) υ(t) = 1 συν(10t + 3π/2) α(t) = - 10 ημ(10t + 3π/2)
ΣF = m1 a = - 20 ημ(10t + 3π/2) Fελατ(x) = - k ( x + Δl ) = - 200 ( x - 0,05 ) = 10 - 200 x
άλλος τρόπος :
ΣF = m1 a => - m1 g ημ30° + Fελατ = m1 a => Fελατ = m1 g ημ30° + m1 a =>
=> Fελατ = 2 10 ½ - 20 ημ(10t + 3π/2) => Fελατ(t) = 10 - 20 ημ(10t + 3π/2)
β) ισορροπία συσσωματώματος : (m1 + m2) g ημ30° = k Δχ => 6 10 ½ = 200 Δχ => Δχ = 0,15 m
η θέση ισορροπίας του συσσωμαώματος συμπίπτει με την κάτω ακραία θέση ταλαντώσεως του Σ1
k = (m1 + m2) (ω')2 => 200 = 6 (ω')2 => ω' = 10 / √3 rad/s T = 2π/ω' = π√3/5 s f = 1/T = 5/π√3 Hz
διατήρηση ορμής για την πλαστική κρούση:
m1 0 + m2 v0 συν30 = (m1 + m2) u => 4 √3 √3/2 = 6 u => u = + 1 m/s
Qκρούσεως = Κτελ - Καρχ = ½ (m1 + m2) u2 - ½ m2 v02 = ½ 6 12 - ½ 4 √32 = 3 - 6 = - 3 Joule
μεταβολή της ορμής για το Σ1 : Δp1 = m1 u - m1 0 = 2 kg 1 m/s => Δp1 = + 2 kg m/s
μεταβολή της ορμής για το Σ2 : Δp2 = m2 u - m2 v0 συν30 = 4 kg 1 m/s - 4 kg √3 √3/2 m/s =>
Δp2 = - 2 kg m/s
το συσσωμάτωμα αμέσως μετά την κρούση έχει ταχύτητα που έχει μέτρο 1 m/s επί του κεκλιμένου επιπέδου προς τα επάνω (θετικά) ενώ βρίσκεται σε θετική απομάκρυνση x = 0,2 m από την νέα θέση ισορροπίας (του συσσωματώματος) οπότε το πλάτος ταλάντωσης του συσσωματώματος είναι : ½ k x2 + ½ (m1 + m2) u2 = ½ k A2 =>
=> 200 0,22 + 6 1 = 200 A2 => 8 + 6 = 200 A2 => A2 = 0,07 => A = 0,1√7 m
x(t) = 0,1√7 ημ(10/ √3 t + θ) υ(t) = √(7/3) συν(10/ √3 t + θ) α(t) = - 10√7 ημ(10/ √3 t + θ)
x(0) = 0,2 => 0,1√7 ημθ = +0,2 => ημθ = + 2 / √7 συνθ = ± √ ( 1 - 4/7 ) = ± √(3/7)
υ(0) = +1 m/s => √(7/3) συνθ = +1 => συνθ = + √(3/7)

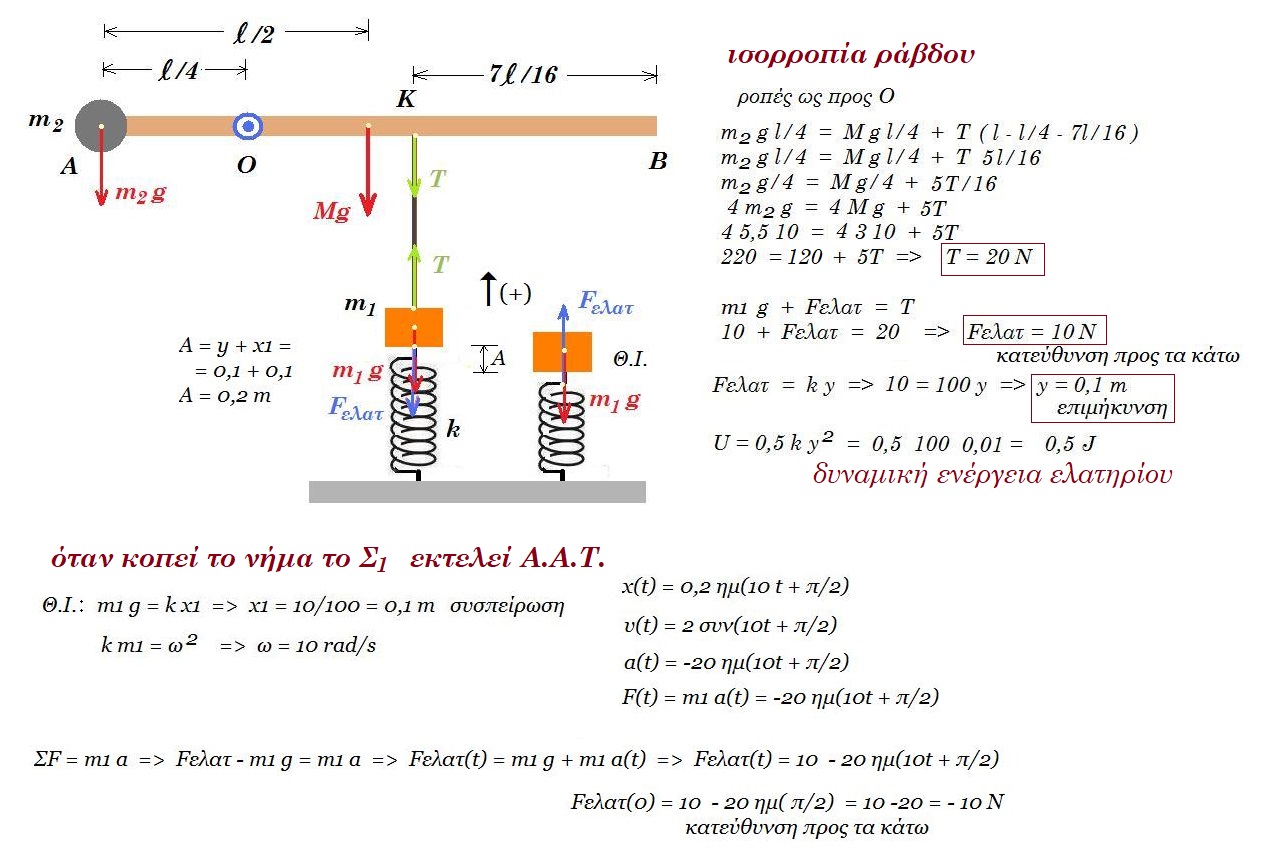

Θέμα 11. 2017
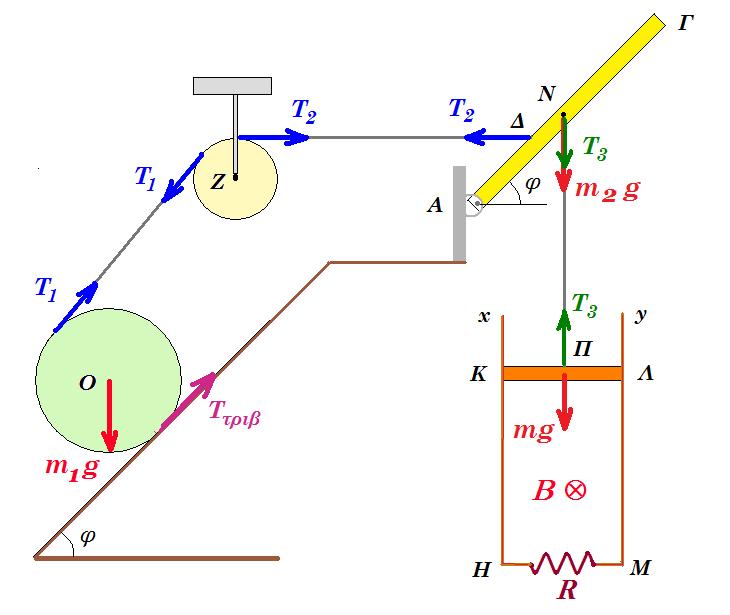
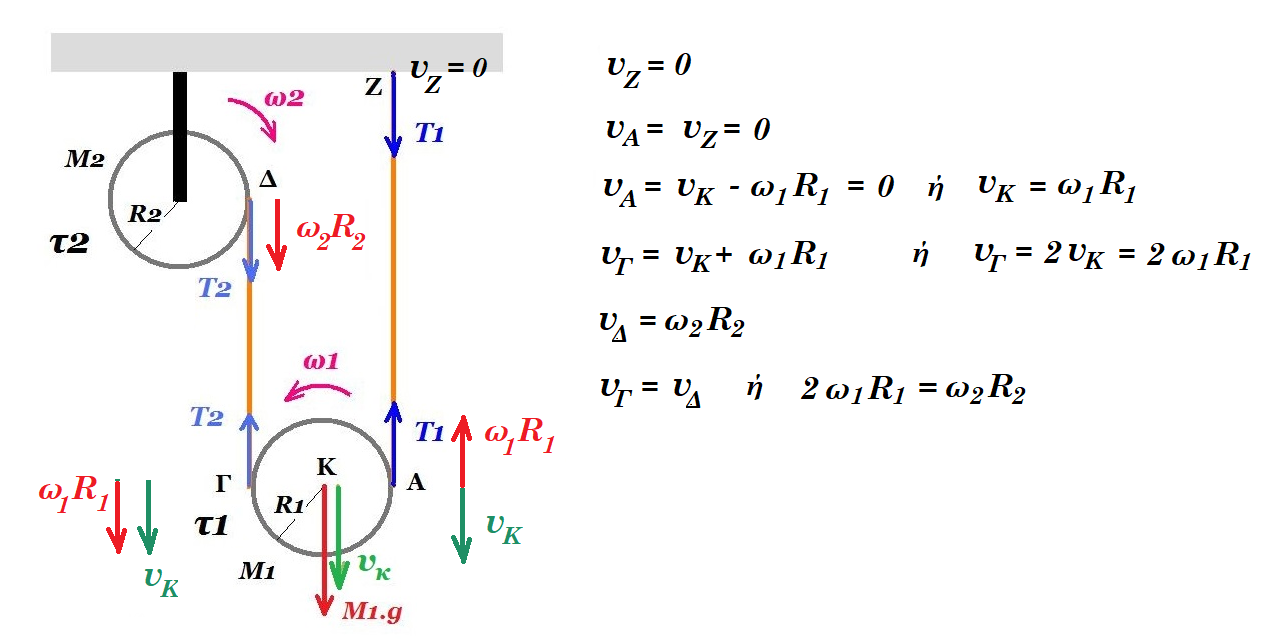
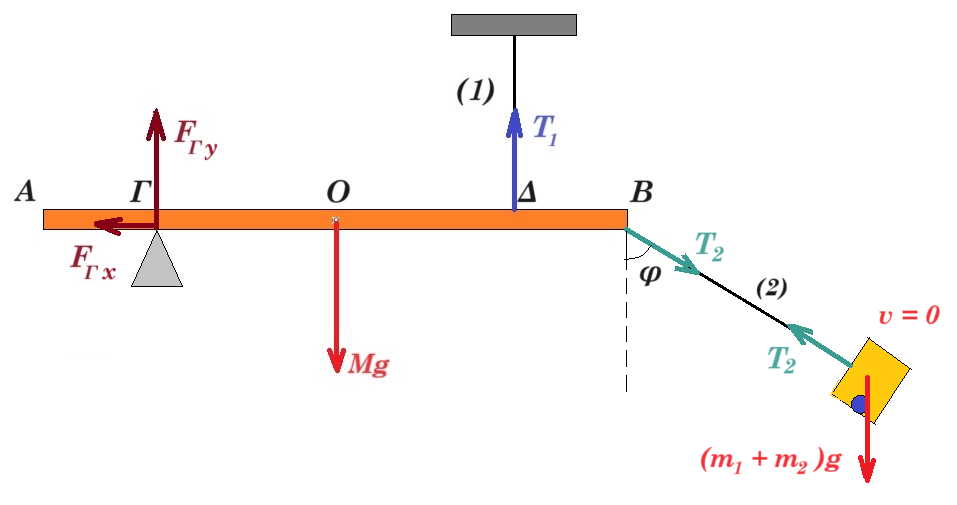
Μία ομογενής άκαμπτη ράβδος ΑΓ σταθερής διατομής έχει μάζα Μ = 4 Kg. Η ράβδος ισορροπεί σε οριζόντια θέση και το άκρο της Α συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Το άλλο άκρο Γ της ράβδου συνδέεται μέσω αβαρούς μη εκτατού νήματος ΓΔ με τον κατακόρυφο τοίχο. Το νήμα σχηματίζει με τη ράβδο γωνία φ. Γύρω από ένα λεπτό ομογενή δίσκο κέντρου Κ, μάζας m = 2 kg και ακτίνας R = 0,1 m είναι τυλιγμένο πολλές φορές ένα λεπτό μη εκτατό αβαρές νήμα. Το ελεύθερο άκρο του νήματος έχει στερεωθεί στο άκρο Γ της ράβδου ΑΓ, όπως φαίνεται στο σχήμα
Τη χρονική στιγμή t0=0 ο δίσκος αφήνεται να κινηθεί και το νήμα ξετυλίγεται χωρίς να ολισθαίνει.
Δ1. Να υπολογίσετε την τάση του νήματος που ασκείται στον δίσκο εάν αυτός κατέρχεται με γωνιακή επιτάχυνση αγων = + 200/3 rad/s2.
Δ2. Να υπολογίσετε την δύναμη που δέχεται η ράβδος ΑΓ στο άκρο της Γ από το νήμα ΓΔ, όταν ο δίσκος κατέρχεται καθώς και την δύναμη που δέχεται η ράβδος ΑΓ στο άκρο της Α από την άρθρωση.
Τη χρονική στιγμή που το κέντρο μάζας Κ του δίσκου έχει κατέλθει κατακόρυφα κατά h1=0,3m το νήμα που συνδέει το δίσκο με τη ράβδο κόβεται.
Δ3. Να υπολογίσετε την στροφορμή μιας στοιχειώδους μάζας Δm = 1 mg της περιφέρειας του δίσκου ως προς τον άξονα περιστροφής του, μετά από χρονικό διάστημα Δt από τη στιγμή που κόπηκε το νήμα.
Δ4. Ποια στιγμή από τη στιγμή t0=0 ο δίσκος έχει κινητική ενέργεια λόγω μεταφοράς Κ = 9 J;
g = 10 m/s2 ημφ = 0,8 συνφ = 0,6 ο άξονας περιστροφής του δίσκου παραμένει συνεχώς οριζόντιος και κινείται σε κατακόρυφη τροχιά σε όλη τη διάρκεια της κίνησης του, ο δίσκος δεν φτάνει στο έδαφος στη διάρκεια του φαινομένου. Θετική φορά προς τα κάτω.
Δ1. επιτάχυνση : α = αγων R = +200/3 rad/s2 0,1 m => α = +20/3 m/s2
για τον δίσκο : ΣF = m a => mg - T1 = m a => 20 - T1 = 2 20/3 => Τ1 = 20 - 40/3 = 20/3 Ν
η τάση νήματος για τον δίσκο είναι Τ1 = - 20/3 Ν και για την ράβδο στο άκρο Γ είναι Τ1' = +20/3 Ν
Δ2.
ροπές ως προς Α : T2 ημφ l - M g l/2 - T1 l = 0 => T2 0,8 - 4 10 / 2 - 20/3 = 0 =>
=> T2 0,8 = 20 + 20/3 => T2 = 80/3 / 0,8 => T2 = 100/3 Ν
ΣFx = 0 => FAx = T2x = T2 συνφ => FAx = 100/3 0,6 = 20 Ν
ΣFy = 0 => T1 + Mg - FAy - T2y = 0 =>
=> FAy = T1 + Mg - T2 ημφ = 20/3 + 40 - 0,8 100/3 => FAy = 20 Ν
FA2 = FAx2 + FAy2 = 202 + 202 => FA = 20√2 Ν
Δ3.
h = ½ a t2 => 0,3 = ½ 20/3 t2 => t = 0,3 s τότε υ = α t = 20/3 0,3 => v = 2 m/s
ω = αγων t = 200/3 0,3 = 20 rad/s = σταθερή διότι από τη στιγμή που κόβεται το νήμα δεν δέχεται ροπή ο δίσκος διότι Τ1 = 0
στροφορμή : L = Δm v r = Δm ω r2 = 0,001 kg 20 rad/s (0,1 m)2 => L = +0,0002 kg m2/s
Δ4.
τη στιγμή που κόβεται το νήμα ( 0,3 s ) ο δίσκος έχει ταχύτητα μέτρου 2 m/s
ΣFy = m α => m g = m a => a = g = 10 m/s2
Kμεταφορική = ½ m υ2 => 9 J = ½ 2 kg v2 => v = 3 m/s
τότε v = v0 + α Δt => 3 m/s = 2 m/s + 10 m/s2 Δt => Δt = 0,1 s
άρα την χρονική στιγμή 0,3 s + 0,1 s = 0,4 s
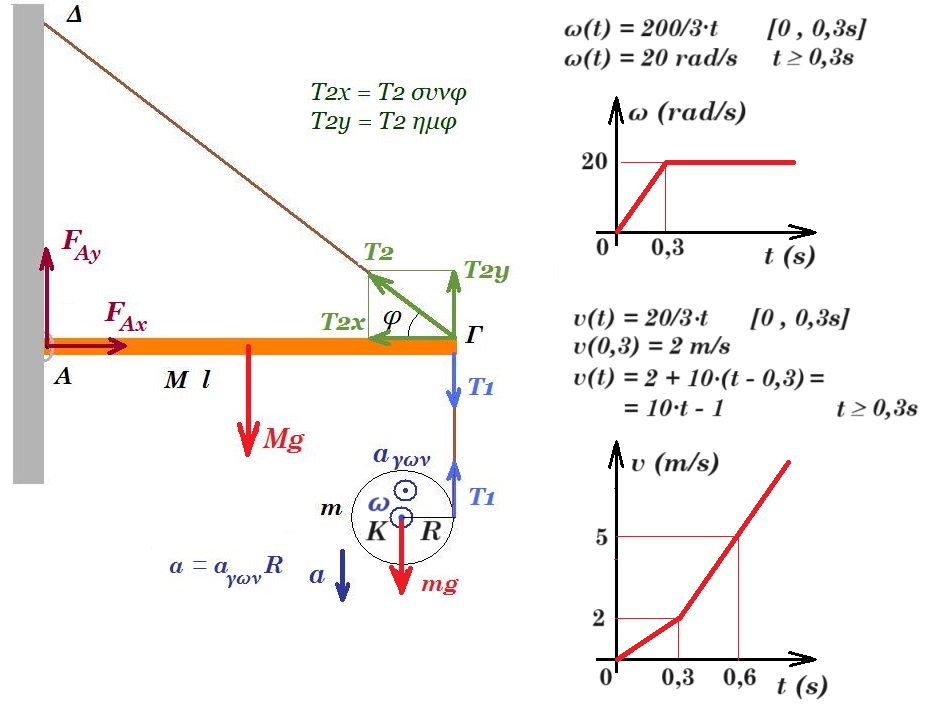
Θέμα 12.
Στο παρακάτω σχήμα φαίνεται η κάθετη τομή ενός καρουλιού, που αποτελείται από ένα κύλινδρο μάζας Μ1 =4 kg και ακτίνας R1 = 0,2 m και από δύο πανομοιότυπους δίσκους μάζας Μ2 =1 kg και ακτίνας R2 = 0,4m ο καθένας. Το καρούλι βρίσκεται σε τραχύ οριζόντιο δάπεδο. Γύρω από τον κύλινδρο έχουμε τυλίξει ένα αβαρές, λεπτό και μη εκτατό νήμα, στο ένα ελεύθερο άκρο του οποίου ασκούμε μία σταθερή δύναμη μέτρου F = 100 N. Το άλλο ελεύθερο άκρο του νήματος συνδέεται με σώμα Σ μάζας m =10 kg, το οποίο βρίσκεται πάνω σε λείο οριζόντιο επίπεδο δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k = 1000 Ν/m, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο σε κατακόρυφο τοίχο.  Αρχικά το σύστημα ισορροπεί και τη χρονική στιγμή t0 = 0 το νήμα που συνδέει το καρούλι με το σώμα Σ κόβεται, οπότε το σώμα Σ εκτελεί απλή αρμονική ταλάντωση πλάτους Α και σταθεράς επαναφοράς D=k, ενώ το καρούλι ξεκινά να κυλίεται χωρίς να ολισθαίνει .
Αρχικά το σύστημα ισορροπεί και τη χρονική στιγμή t0 = 0 το νήμα που συνδέει το καρούλι με το σώμα Σ κόβεται, οπότε το σώμα Σ εκτελεί απλή αρμονική ταλάντωση πλάτους Α και σταθεράς επαναφοράς D=k, ενώ το καρούλι ξεκινά να κυλίεται χωρίς να ολισθαίνει .
Δ1. Να γράψετε την εξίσωση της απομάκρυνσης σε συνάρτηση με το χρόνο για την απλή αρμονική ταλάντωση του σώματος Σ. Θεωρείστε θετική φορά προς τα δεξιά.
Δ2. Τη χρονική στιγμή t1, όπου το σώμα Σ βρίσκεται στη μέγιστη απομάκρυνση από τη θέση ισορροπίας για πρώτη φορά, να υπολογίσετε το μέτρο της ταχύτητας του ανώτερου σημείου του δίσκου του καρουλιού, αν η γωνιακή επιτάχυνση περιστροφής περί τον άξονα του είναι αγων=+50rad/s2.
Δ3. Να υπολογίσετε το ρυθμό μεταβολής της κινητικής ενέργειας του σώματος Σ τη στιγμή t1.
Δ4. Να υπολογίσετε το έργο της δύναμης F από τη χρονική στιγμή t = 0 έως τη χρονική στιγμή t1.
Τη χρονική στιγμή t1 το νήμα που ήταν τυλιγμένο στον κύλινδρο εγκαταλείπει το καρούλι και ασκούμε ακαριαία στο κέντρο μάζας του καρουλιού μία οριζόντια δύναμη μέτρου F1 =30 Ν με αποτέλεσμα το καρούλι να αποκτήσει γωνιακή επιτάχυνση α'γων = -10 rad/s2 και να ακινητοποιηθεί τη χρονική στιγμή t2.
Δ5. Να υπολογίσετε το συνολικό αριθμό περιστροφών από τη χρονική στιγμή t = 0 έως τη χρονική στιγμή t2, κατά την οποία το καρούλι ακινητοποιείται.
Δ1.
ισορροπία σώματος Σ : Fελατ = Τ => k x0 = T (1)
ισορροπία καρουλιού : ΣF = 0 => F - T + Ττριβ = 0 (2)
Στ(Κ) = 0 => F R1 + T R1 = Ττριβ R2 => F 0,2 + T 0,2 = Ττριβ 0,4 => F + T = 2 Ττριβ (3)
(2) + (3) => 2 F = Ττριβ => Ττριβ = 2 100 Ν = 200 Ν οπότε η (3) => Τ = 100 + 200 = 300 Ν
και από (1) => x0 = T/ k = 300 / 1000 => x0 = 0,3 m αρχική επιμήκυνση ελατηρίου
ω2 = k / m = 1000 / 10 => ω = 10 rad/s x(t) = 0,3 ημ(10t + π/2)
υ(t) = 3 συν(10t + π/2) a(t) = - 30 ημ(10t + π/2)
Δ2.
η χρονική στιγμή είναι : t1 = Τ/2 = π/10 s
αγων = 50 rad/s επιτάχυνση a(Κ) = R2 αγων = 0,4 50 = 20 m/s2
v(Κ) = a t1 = 20 m/s2 π/10 s = 2π m/s ταχύτητα κέντρου μάζας καρουλιού
η ταχύτητα του του ανώτερου σημείου του δίσκου του καρουλιού : 2 2π m/s = 4π m/s
Δ3.
ο ρυθμός μεταβολής της κινητικής ενέργειας του Σ είναι :
dK/dt = m a v = 10 [- 30 ημ(10t + π/2)] 3 συν(10t + π/2) = - 900 ημ(10t + π/2) συν(10t + π/2)
τη στιγμή t = π/10 s dK/dt = - 900 ημ(π + π/2) συν(π + π/2) = - 900 (-1) 0 => dK/dt = 0
Δ4. το κέντρο μάζας Κ του καρουλιού μετατοπίζεται κατά x1 = ½ α t12 = ½ 20 (π/10)2 = 1 m
το νήμα ξετυλίγεται κατά l = θ1 R1 = ½ αγων t12 R1 = ½ 50 (π/10)2 0,2 = 2,5 rad 0,2 m = 0,5 m
το σημείο εφαρμογής της F μετατοπίζεται κατά : x1 + l = 1,5 m
έργο της F : WF = F ( x1 + l ) = 100 1,5 => WF = 150 J
Δ5. θ1 = ½ αγων t12 = ½ 50 (π/10)2 = 2,5 rad
o αριθμός περιστροφών : Ν1 = θ1 / 2π = 2,5 rad / 2π = 5/4π περιστροφές
η γωνιακή ταχύτητα : ω1 = αγων t1 = 50 π/10 => ω1 = 5π rad/s
α'γων = - 10 rad/s2 ω2 = ω1 + αγων Δt => 0 = 5π + (-10) Δt => Δt = π/2 s
θ2 = ω Δt + ½ αγων Δt2 = 5π π/2 + ½ (-10) (π/2)2 = 25 - 12,5 = 12,5 rad π2 = 10
N2 = θ2 / 2π = 12,5 / 2π = 25/4π περιστροφές
συνολικός αριθμός περιστροφών = 5/4π + 25/4π = 30/4π = 15/2π
Θέμα 13.
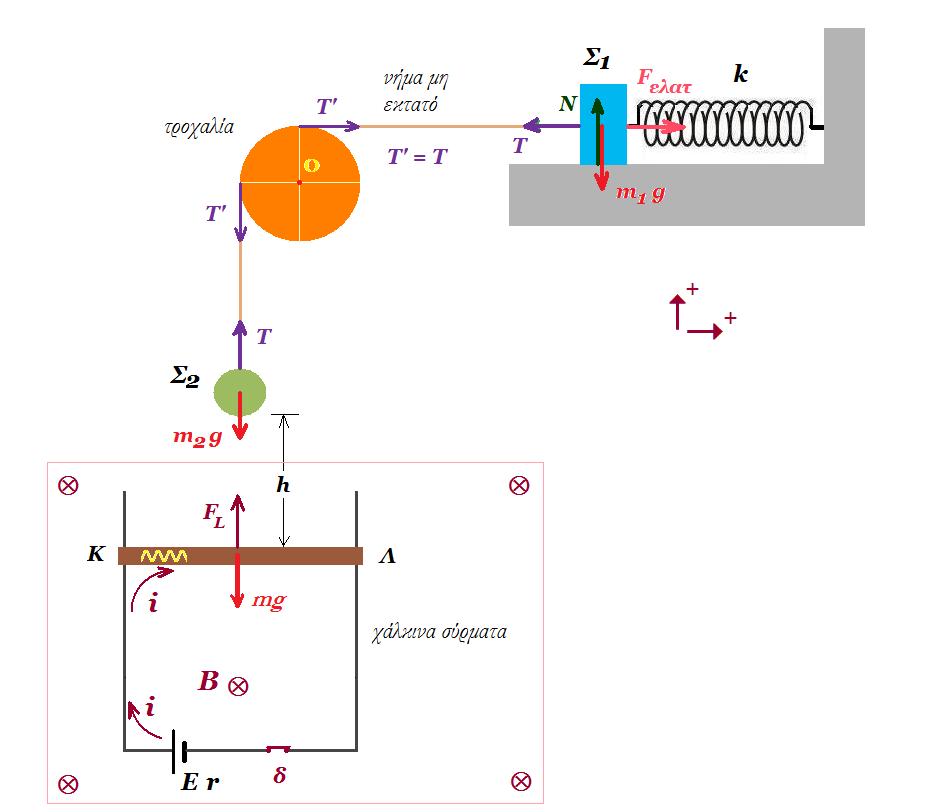
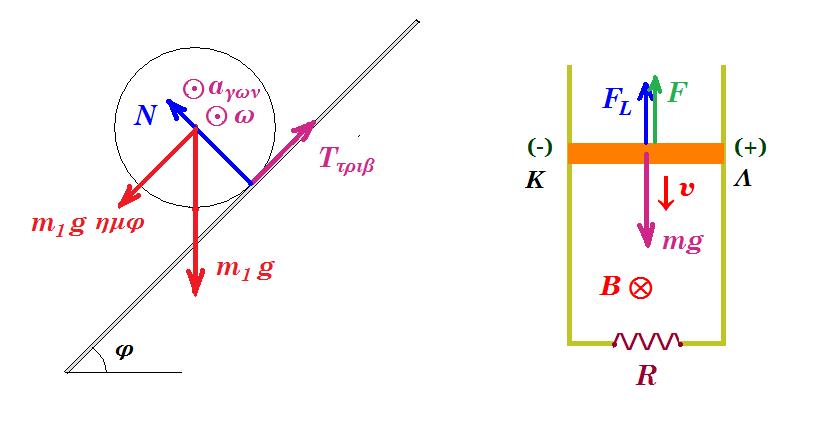
Στο σύστημα του σχήματος βλέπουμε τον ομογενή κύλινδρο κέντρου Ο, μάζας m1 = 6 kg και ακτίνας ρ να ισορροπεί πάνω στο κεκλιμένο επίπεδο με τη βοήθεια νήματος (παράλληλο στο κεκλιμένο επίπεδο) το οποίο αφού περάσει από τροχαλία κέντρου Ζ ακτίνας b καταλήγει στο σημείο Δ της ομογενούς ράβδου ΑΓ που έχει μάζα m2. Η ράβδος ΑΓ στηρίζεται σε ακλόνητο σημείο μέσω άρθρωσης Α. Η απόσταση ΑΔ είναι d/3, όπου d το μήκος της ράβδου. Οι γωνίες φ έχουν ημφ = 0,6 και συνφ = 0,8. Στο κέντρο Ν της ράβδου έχει δεθεί νήμα που καταλήγει στο κέντρο ομογενούς αγωγού ΚΛ μάζας m = 0,8 kg η οποία ισορροπεί σε επαφή με δύο λείες κατακόρυφες αγώγιμες ράγες αμελητέας αντίστασης.
Α. Να υπολογιστεί η μάζα m2 της ράβδου ΑΓ αν όλο το σύστημα ισορροπεί.
Κόβουμε το νήμα ΝΠ και ο αγωγός ΚΛ, μήκους L = 1 m, αντίστασης r = 1 Ω ελευθερώνεται και κατεβαίνει τις ράγες χωρίς τριβές, ενώ το μαγνητικό πεδίο έχει ένταση B = 2 Τ. Οι ράγες συνδέονται στο κάτω μέρος τους με αντίσταση R = 3 Ω. Από τη στιγμή t0 = 0 που κόβεται το νήμα ο αγωγός ΚΛ δέχεται σταθερή κατακόρυφη δύναμη F = 6 N με φορά προς τα επάνω.
Β. Να δείξετε ότι ο αγωγός ΚΛ αποκτάει κάποια στιγμή οριακή ταχύτητα και να την υπολογίσετε.
Γ. Αν από τη στιγμή που κόπηκε το νήμα και ξεκίνησε μέχρι να αποκτήσει οριακή ταχύτητα έπεσε κατά y = 1 m να υπολογίσετε τη θερμότητα Joule που εκλύθηκε σε κάθε αντιστάτη στο διάστημα αυτό.
Δ. Πόσο φορτίο μετακινήθηκε μέσα από τον αγωγό κατά την πτώση y = 1 m;
Ε. Μετά το κόψιμο του νήματος απελευθερώνεται και ο κύλινδρος και κατεβαίνει το κεκλιμένο επίπεδο. Για ποιες τιμές του συντελεστή οριακής τριβής είναι δυνατή η κύλιση του κυλίνδρου χωρίς ολίσθηση εάν κυλίεται με γωνιακή επιτάχυνση αγων = 20 rad/s2 και η ακτίνα του είναι ρ = 0,2 m;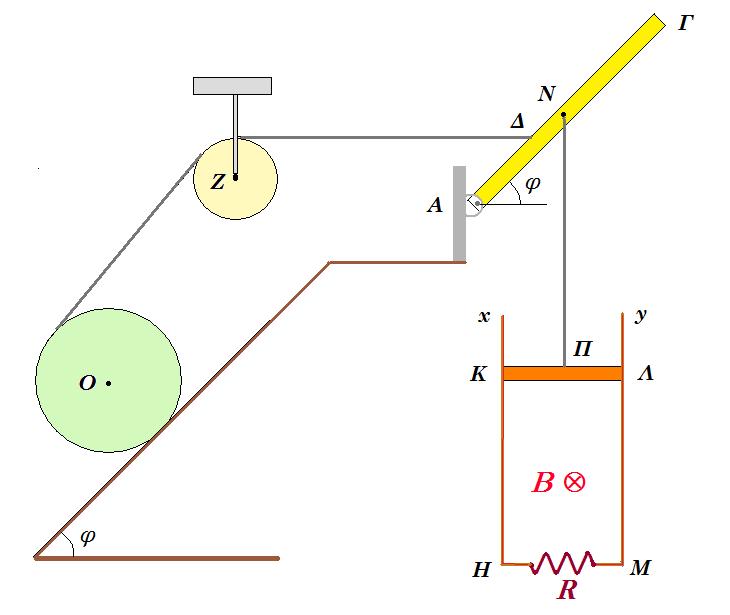
(Α) ισορροπία ράβδου ΚΛ : m g = T3 => T3 = 0,8 10 => Τ3 = 8 Ν
ισορροπία ράβδου ΑΓ :
ροπές ως προς Α : Στ(Α) = 0 => T2 d/3 ημφ - m2 g d/2 συνφ - T3 d/2 συνφ = 0
=> T2 1/3 0,6 - m2 g 1/2 0,8 = 8 1/2 0,8 => 0,2 T2 - m2 10 0,4 = 8 0,4 => T2 - 20 m2 = 16
ισορροπία τροχαλίας :
ροπές ως προς Ζ : Στ(Ζ) = 0 => Τ2 b = T1 b => Τ2 = T1
ισορροπία κυλίνδρου :
ροπές ως προς Ο : Στ(Ο) = 0 => Τ1 ρ = Tτριβ ρ => T1 = Tτριβ
ΣFx = 0 => m1 g ημφ - T1 - Tτριβ = 0 => 6 10 0,6 - T1 - T1 = 0 => Τ1 = 18 Ν
άρα Τ2 = T1 = 18 Ν
οπότε από την σχέση : T2 - 20 m2 = 16 => 18 - 20 m2 = 16 => m2 = 0,1 kg
(Β) τα ηλεκτρόνια της ράβδου δέχονται δύναμη Lorenz και μετακινούνται προς το άκρο Κ που φορτίζεται αρνητικά, αναπτύσσεται επαγωγική τάση στα άκρα Λ(+), Κ(-) της ράβδου Εεπαγ = Β l v
οπότε το κύκλωμα διαρρέεται με ρεύμα εντάσεως i = Εεπαγ / (R + r) = Β l v / (R + r)
στη ράβδο ασκείται δύναμη Laplace FL = B i l = Β2 l2 v / (R + r)
για την κίνηση της ράβδου έχουμε : θετική κατεύθυνση κατακόρυφη προς τα κάτω
ΣF = m a => m g - FL - F = m a => m g - Β2 l2 v / (R + r) - F = m a
καθώς η ραβδος κατέρχεται αυξάνεται η ταχύτητα με συνέπεια να μειώνεται η επιτάχυνση έως ότου μηδενισθεί οπότε η ράβδος θα αποκτήσει σταθερή ταχύτητα ( οριακή )
α = 0 => m g - F = Β2 l2 v / (R + r) => υ = ( m g - F ) (R + r) / Β2 l2 =>
=> υ = ( 0,8 10 - 6 ) (3+1) / 4 1 = 2 m/s οριακή ταχύτητα
(Γ) m g y - F y + Q = ½ m v2 => Q = ½ m v2 - m g y + F y >
=> Q = ½ 0,8 22 - 0,8 10 1 + 6 1 => Q = 1,6 - 8 + 6 = - 0,4 J
Q(r) = i2 r t Q(R) = i2 R t Q(r) / Q(R) = r / R = 1/3
Q(r) + Q(R) = |Q| = 0,4 J άρα Q(r) = 0,1 J και Q(R) = 0,3 J
(Δ) q = ΔΦ / (r + R) = Β Α / (r + R) = B l y / (r + R) = 2 1 1 / 4 = 0,5 C
(E) επιτάχυνση κυλίνδρου : α = αγων ρ = 20 rad/s2 0,2 m = 4 m/s2
ΣFx = m1 g ημφ - Ττριβ = m1 a => 0,8 10 0,6 - Ττριβ = 0,8 4 => Ttτριβ = 1,6 Ν
ΣFy = 0 => m1 g συνφ = Ν => Ν = 0,8 10 0,8 = 6,4 Ν
ο συντελεστής τριβής κυλίσεως : μ = Τ / Ν = 1,6 / 6,4 = 0,25
μαθηματική ανάλυση :
m g - Β2 l2 v / (R + r) - F = m a => 8 - 4 v / 4 - 6 = 0,8 a => 2 - v = 4/5 dv/dt =>
=> dv / (v - 2) = - 5/4 dt => ln [ (v - 2) / (- 2) ] = - 5/4 dt => v(t) = 2 ( 1 - e-5/4 t )
a = dv/dt => a(t) = 2,5 e-5/4 t dx = v dt = 2 ( 1 - e-5/4 t ) dt => x(t) = 2t + 1,6 ( e-5/4 t - 1 )
i = Εεπαγ / (R + r) = Β l v / (R + r) = ( 2 1 / 4 ) 2 ( 1 - e-5/4 t ) => i(t) = 1 - e-5/4 t
FL = B l i = 2 1 ( 1 - e-5/4 t ) => FL(t) = 2 ( 1 - e-5/4 t )
PFL = FL v = 2 ( 1 - e-5/4 t ) 2 ( 1 - e-5/4 t ) => PFL(t) = 4 ( 1 - e-5/4 t )2
i = dq/dt => dq = i dt = ( 1 - e-5/4 t ) dt => q(t) = t + 0,8 ( e-5/4 t - 1 )
Pw = mg v = 8 2 ( 1 - e-5/4 t ) => Pw(t) = 16 ( 1 - e-5/4 t )
PF = F v = 6 2 ( 1 - e-5/4 t ) => PF(t) = 12 ( 1 - e-5/4 t )
Pw(t) - PFL(t) - PF(t) = 16 ( 1 - e-5/4 t ) - 4 ( 1 - e-5/4 t )2 - 12 ( 1 - e-5/4 t ) =
= ( 1 - e-5/4 t ) [ 16 - 4 ( 1 - e-5/4 t ) - 12 ] = ( 1 - e-5/4 t ) 4 e-5/4 t =
= 0,8 2 ( 1 - e-5/4 t ) 2,5 e-5/4 t = m v a
τ = 4/5 s = 0,8 s 5τ = 4 s
x(4) = 2 4 + 1,6 (e-5/4 4 - 1) = 8 + 1,6 ( 0,0067 - 1 ) = 6,4 m
v(4) = 2 ( 1 - e-5/4 4 ) = 2 ( 1 - 0,0067 ) = 2 m/s
a(4) = 2,5 e-5/4 t = 2,5 0,0067 = 0,017 m/s2
i(4) = 1 - e-5/4 4 = 1 - 0,0067 = 0,9933 A = 1A
q(4) = 4 + 0,8 (e-5/4 4 - 1) = 4 + 0,8 ( 0,0067 - 1 ) = 3,2 C
PFL = 4 ( 1 - e-5/4 t )2 = 4 - 8 e-5/4 t + 4 e-5/2 t
WFL(t) = 4 t + 6,4 ( e-5/4 t - 1 ) - 1,6 ( e-5/2 t - 1 )
WFL(t) = 4 t + 6,4 e-5/4 t - 1,6 e-5/2 t - 4,8
WFL(4) = 4 4 + 6,4 e-5/4 4 - 1,6 e-5/2 4 - 4,8 = 16 + 6,4 0,0067 - 1,6 0,000045 - 4,8 = 16 + 0 - 0 - 4,8 = 11,2 J
m g x(4) - 0,5 m v(4)2 - F x(4) = 0,8 10 6,4 - 0,5 0,8 22 - 6 6,4 = 11,2 J = WFL(4)
Θέμα 14.
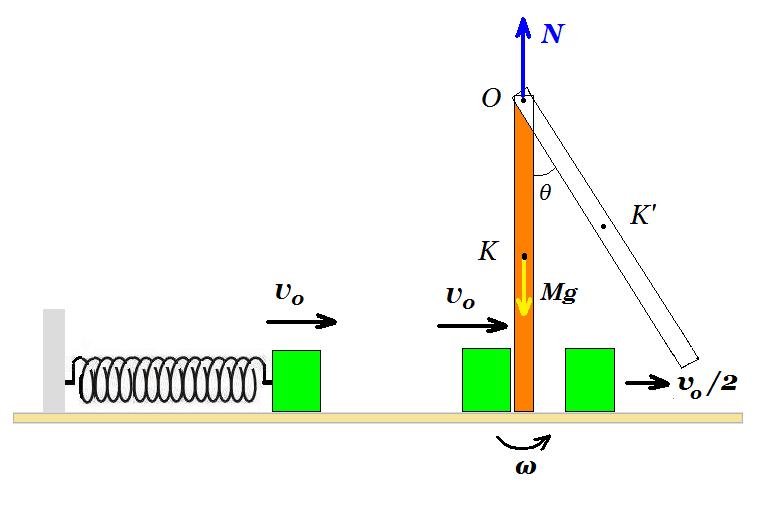
Σώμα μάζας m=1kg δεμένο στο ελεύθερο άκρο οριζόντιου και στερεωμένου ελατηρίου κάνει Α.Α.Τ. με μέγιστη κινητική ενέργεια K0=2J και πλάτος Α=0,2m. Τη χρονική στιγμή t0=0 το σώμα βρίσκεται στη θέση x=-0,2m. Τη στιγμή t1 που το σώμα m περνάει για πρώτη φορά από τη θέση ισορροπίας κινούμενο προς την πλευρά που το ελατήριο επιμηκύνεται κόβεται το ελατήριο και το σώμα συνεχίζει μόνο του πάνω στο λείο οριζόντιο επίπεδο.
Α. Να γραφεί η εξίσωση της δύναμης επαναφοράς της Α.Α.Τ. του σώματος και η εξίσωση του ρυθμού μεταβολής της κινητικής ενέργειας του σώματος συναρτήσει του χρόνου
Β. Να υπολογιστούν η χρονική στιγμή t1 και η ταχύτητα του σώματος τη στιγμή που κόβεται το ελατήριο.
Το σώμα μετά συγκρούεται με το άκρο Δ, ράβδου μήκους d=1m, μάζας Μ=2kg το ένα άκρο της οποίας είναι στερεωμένο στο σημείο Ο, και μπορεί να στρέφεται χωρίς τριβές. Μετά την κρούση το σώμα m συνεχίζει την κίνησή του στην ίδια κατεύθυνση με ταχύτητα μέτρου ίσου με το μισό αυτής που είχε πριν την κρούση ενώ η ράβδος αποκτά κινητική ενέργεια λόγω περιστροφής Κρ,περ. = 0,75 J και γωνιακή ταχύτητα ω = 1,5 rad/s. Η κρούση διαρκεί χρονικό διάστημα Δt=0,02s.
Γ. Να υπολογιστούν :
Γ1. η ροπή τ που άσκησε το σώμα στη ράβδο κατά την κρούση, αν η ροπή θεωρηθεί σταθερή
Γ2. η απώλεια της μηχανικής ενέργειας του συστήματος, «σώμα - ράβδος» λόγω κρούσης
Γ3. το μέτρο της δύναμης που ασκεί ο άξονας, Ο, στη ράβδο αμέσως μετά την κρούση
Γ4. το συνημίτονο της γωνίας θ που σχηματίζει η ράβδος με την κατακόρυφο τη στιγμή που σταματά στιγμιαία.
Α. K0 = ½ k A2 => 2 J = ½ k (0,2m)2 => k = 100 N/m
k = m ω2 => 100 = 1 ω2 => ω = 10 rad/s T = 2π/ω = π/5 sec x(t) = 0,2 ημ(10t + 3π/2)
υ(t) = 2 συν(10t + 3π/2) α(t) = - 20 ημ(10t + 3π/2)
ΣF = m a = 1 ( - 20 ημ(10t + 3π/2) ) => ΣF = - 20 ημ(10t + 3π/2) = - 100 0,2 ημ(10t + 3π/2) = - 100 x = - k x = Fελατ - 0,2 m £ x £ + 0,2 m
Fελατ = - k x => Fελατ = - 100 x - 0,2 m £ x £ + 0,2 m
dK/dt = m v dv/dt = m v a = 1 2 συν(10t + 3π/2) { - 20 ημ(10t + 3π/2) } =
= - 40 ημ(10t + 3π/2) συν(10t + 3π/2) = - 20 ημ(20t + 3π)
dU/dt = k x dx/dt = k x v = 100 0,2 ημ(10t + 3π/2) 2 συν(10t + 3π/2) =
= 40 ημ(10t + 3π/2) συν(10t + 3π/2) = 20 ημ(20t + 3π)
Β. το ελατήριο κόβεται τη στιγμή που το σώμα περνά για 1η φορά από τη Θ.Ι. δηλαδή t = T/4 = π/20 sec η ταχύτητά του είναι η μέγιστη υ = 2 m/s
Γ. λείο επίπεδο, διατήρηση στροφορμής : m v d = m v/2 d + L => 1 2 1 = 1 2/2 1 + L => L = 1 kg.m/s
τ = dL/dt = ( Lμετά - Lπριν ) / dt = ( 1 - 0 ) / 0,02 => τ = 50 N.m
Kπριν = ½ m v2 = ½ 1 22 = 2 J Kμετά = ½ m (v/2)2 + Κρ,περ. = ½ 1 (2/2)2 + 0,75 = 1,25 J
ΔΚ = Kμετά - Kπριν = 1,25 - 2 => ΔΚ = - 0,75 J
ΣFy = Fκεντρομόλος => Ν - Μ g = Μ υ2 / r = M ω2 d/2 => Ν = Μ g + M ω2 d/2 =>
=> Ν = 2 10 + 2 1,52 1/2 => Ν = 22,25 Ν
διατήρηση ενέργειας : Κρ,περ. = Μ g d/2 ( 1 - συνθ ) => 0,75 = 2 10 1/2 ( 1 - συνθ ) =>
=> 3/4 = 10 ( 1 - συνθ ) => συνθ = 1 - 3/40 = 37/40 = 0,925
Θέμα 15.
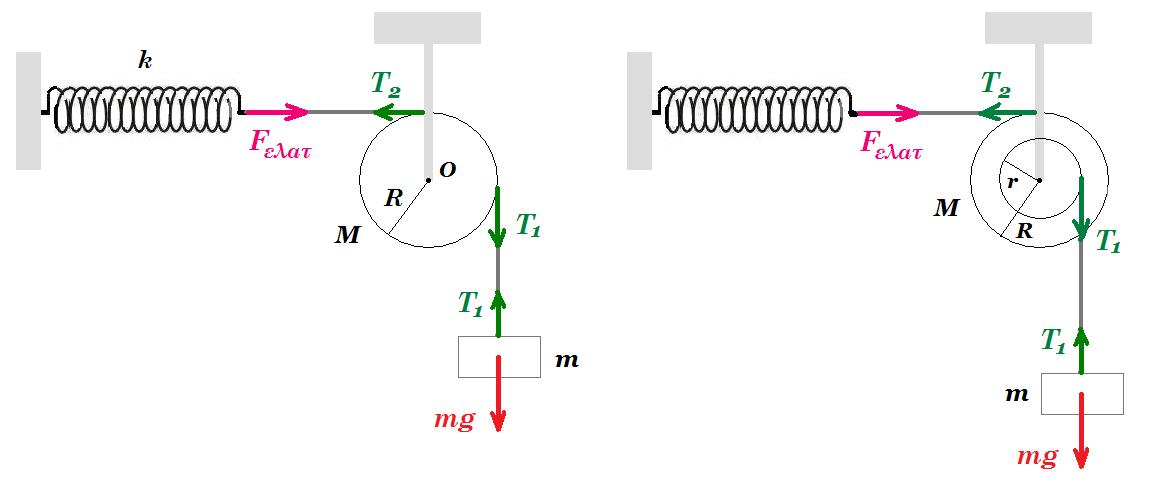
Τροχαλία αμελητέας μάζας, ακτίνας R, είναι στερεωμένη, όπως φαίνεται στο σχήμα και μπορεί να στρέφεται γύρω από τον άξονά της. Από την τροχαλία διέρχεται νήμα στο ένα άκρο του οποίου δένεται νήμα στο ένα άκρο του οποίου δένεται σώμα μάζας m=4kg, ενώ το άλλο άκρο δένεται στο ελεύθερο άκρο ελατηρίου σταθεράς k=100Ν/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε ακλόνητο σημείο. Ανυψώνουμε το σώμα ως το σημείο Α, έτσι ώστε το ελατήριο να έχει το φυσικό του μήκος, ενώ το νήμα είναι τεντωμένο. Αφήνουμε το σώμα ελεύθερο.
A. Εξετάστε αν το σώμα μάζας m κάνει Α.Α.Τ. Θετική φορά όπως το βάρος του σώματος.
B. Πόση είναι η επιτάχυνση του σώματος όταν η επιμήκυνση του ελατηρίου είναι x1=0,2m;
Γ. Πόση είναι η μέγιστη επιμήκυνση του ελατηρίου;
Δ. Πόση πρέπει να είναι η κατακόρυφη μετατόπιση του σώματος μέχρι το σώμα να αποκτήσει μέγιστη ταχύτητα.
E. Πόση είναι η μέγιστη ταχύτητα.
Z. Πόσος είναι ο ρυθμός μεταβολής της κινητικής ενέργειας του συστήματος «τροχαλία - σώμα», όταν η ταχύτητα του σώματος είναι υ=2m/s;
H. Στην δεύτερη διάταξη εξετάστε αν το σώμα μάζας m κάνει Α.Α.Τ. και γράψτε τις εξισώσεις συναρτήσει του χρόνου. Θετική φορά όπως το βάρος του σώματος.
η ροπή αδράνειας της τροχαλίας : Ι(Ο) = ½ Μ R2
(Α) ισορροπία σώματος : m g - T1 = 0
ισορροπία τροχαλίας : Στ(Ο) = 0 => T1 R - T2 R = 0 => T1 = T2
ελατήριο : Τ2 = Fελατ = k Δl τελικά : m g = k Δl => Δl = 4 10 / 100 = 0,4 m αρχική επιμήκυνση του ελατηρίου όταν το σύστημα ισορροπεί
στην τυχαία θέση σώμα : ΣF = m g - T1 = m a (1)
τροχαλία : Στ(Ο) = 0 => T1 R - T2 R = 0 => T1 = T2 (2)
ελατήριο : Τ2 = Fελατ = k ( x + Δl ) (3)
(1) + (2) + (3) => m g = m a + k ( x + Δl ) => m a + k x = 0 => ΣF = - k x
το σώμα εκτελεί ΑΑΤ με συχνότητα ω2 = k /m = 100 / 4 = 25 => ω = 5 rad/s
T = 2π/ω = 2π/5 s
x(t) = 0,4 ημ(5t + 3π/2) υ(t) = 2 συν(5t + 3π/2) α(t) = -10 ημ(5t + 3π/2)
ΣF(t) = m a(t) = -40 ημ(5t + 3π/2)
Fελατ(t)= k ( x + Δl ) = 100 { 0,4 ημ(5t + 3π/2) + 0,4 } = 40 + 40 ημ(5t + 3π/2)
(Β) επιμήκυνση ελατηρίου x1 = 0,2m => x + Δl = 0,2 => x + 0,4 = 0,2 => x = - 0,2 m
τότε 0,4 ημ(5t + 3π/2) = - 0,2 => ημ(5t + 3π/2) = - 0,5
οπότε α = - 10 ημ(5t + 3π/2) = - 10 ( - 0,5 ) => a = +5 m/s2
(Γ) t = 0 Fελατ(t)= k ( x + Δl ) = 40 + 40 ημ(3π/2) = 40 + (- 40) = 0
t = T/2 = π/5 s Fελατ(Τ/2) = 40 + 40 ημ(5 π/5 + 3π/2) = 40 + 40 ημ(π/2) = 80 Ν μέγιστη δύναμη ελατηρίου
η μέγιστη επιμήκυνση είναι Fελατ,max / k = 80 Ν / 100 Ν/m = 0,8 m
(Δ), (Ε) η μέγιστη ταχύτητα του σώματος είναι : 2 m/s από την σχέση :
υ(t) = 2 συν(5t + 3π/2)
η κατακόρυφη μετατόπιση του σώματος όταν έχει μέγιστη ταχύτητα είναι : x = 0,4 m θέση ισορροπίας για την ταλάντωση του σώματος
(Z) ο ρυθμός μεταβολής της κινητικής ενέργειας όταν κατέρχεται με υ = 2 m/s τότε α = 0
συνεπώς dK / dt = m v a = 0
--------------------------------------------------------------------
(Η) ισορροπία σώματος : m g - T1 = 0 r = R/2
ισορροπία τροχαλίας : Στ(Ο) = 0 => T1 r - T2 R = 0 => T1 = 2 T2
ελατήριο : Τ2 = Fελατ = k Δl m g = 2 k Δl => Δl = mg / 2k = 40/200 = 0,2 m αρχική επιμήκυνση του ελατηρίου όταν το σύστημα ισορροπεί
στην τυχαία θέση σώμα : ΣF = m g - T1 = m a (1)
τροχαλία : Στ(Ο) = 0 => T1 r - T2 R = 0 => T1 R/2 - T2 R = 0 => T1 = 2 T2 (2)
ελατήριο : Τ2 = Fελατ = k ( x + Δl ) => 2 Τ2 = 2 k ( x + Δl ) (3)
(1) + (2) + (3) => m g = m a + 2k ( x + Δl ) => 0 = m a + 2 k x => ΣF = - 2 k x
συνεπώς το σώμα εκτελεί ΑΑΤ με συχνότητα ω2 = 2k / m = 200 / 4 = 50 => ω = 5√2 rad/s
x(t) = 0,2 ημ(5√2t + 3π/2) υ(t) = √2 συν(5√2t + 3π/2)
α(t) = - 10 ημ(5√2t + 3π/2) ΣF(t) = m a(t) = - 40 ημ(5√2t + 3π/2)
Fελατ(t) = k ( Δl + x ) = 100 ( 0,2 + x ) = 20 + 100 x = 20 + 20 ημ(5√2t + 3π/2)
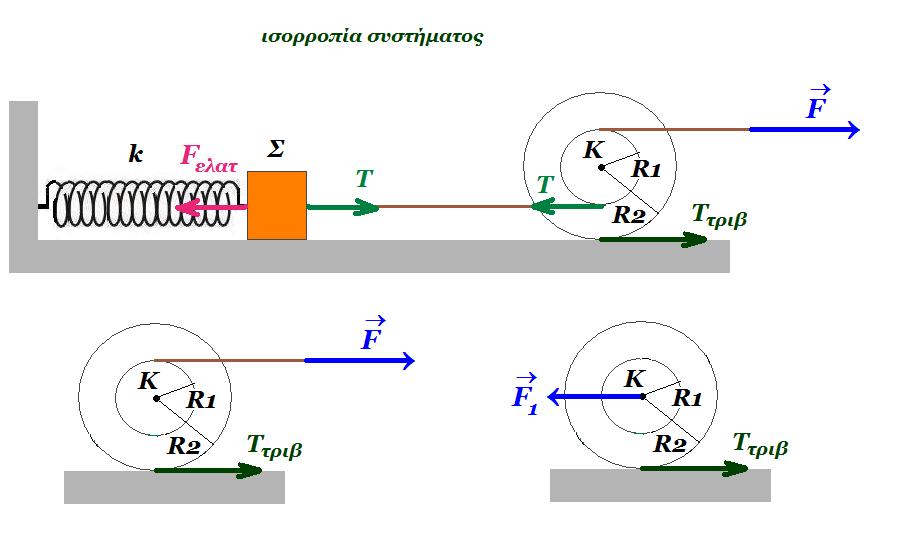
Θέμα 16.
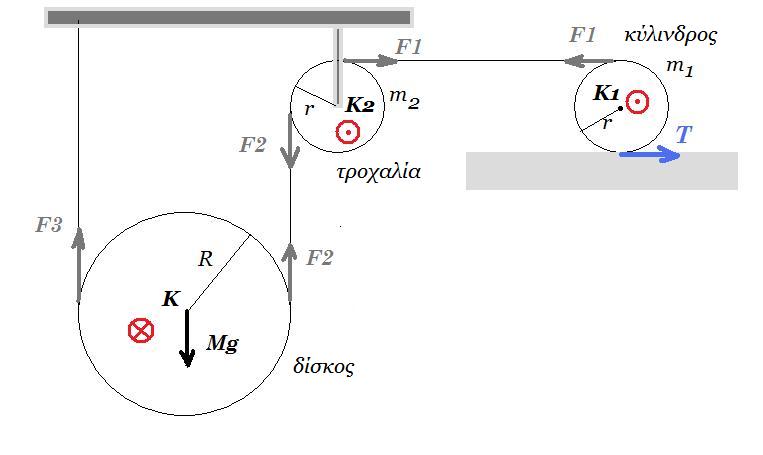
Θέμα 17.
Στο σύστημα που φαίνεται στο σχήμα η μικρή τροχαλία Κ2 είναι μάζας m2=1kg, ακτίνας r και το αβαρές σχοινί συνδέει τον κύλινδρο, Κ1, μάζας m1=8kg, ακτίνας r με το δίσκο, Κ, μάζας Μ=4kg και ακτίνας R. O κύλινδρος κυλίεται χωρίς να ολισθαίνει καθώς το τυλιγμένο σε αυτόν
νήμα ξετυλίγεται . Αν αφήσουμε το σύστημα ελεύθερο τη χρονική στιγμή t0=0, να υπολογιστούν:
Α. η επιτάχυνση α1 του κέντρου μάζας Κ1 του κυλίνδρου εάν ο δίσκος κατέρχεται με επιτάχυνση α = 2 m/s2
Β. η πτώση του κέντρου μάζας του δίσκου, Κ και η μετατόπιση του κέντρου μάζας του κυλίνδρου, Κ1 τη χρονική στιγμή t=2s.
(Α) r αγων,1 = α1 r αγων,2 = r αγων,1 + α1 = 2 α1
α = αγων R r aγων,2 = R αγων + α = 2 a άρα α1 = α = 2 m/s2
(B) y = ½ a t2 = ½ 2 22 = 4 m x1 = ½ a1 t2 = ½ 2 22 = 4 m
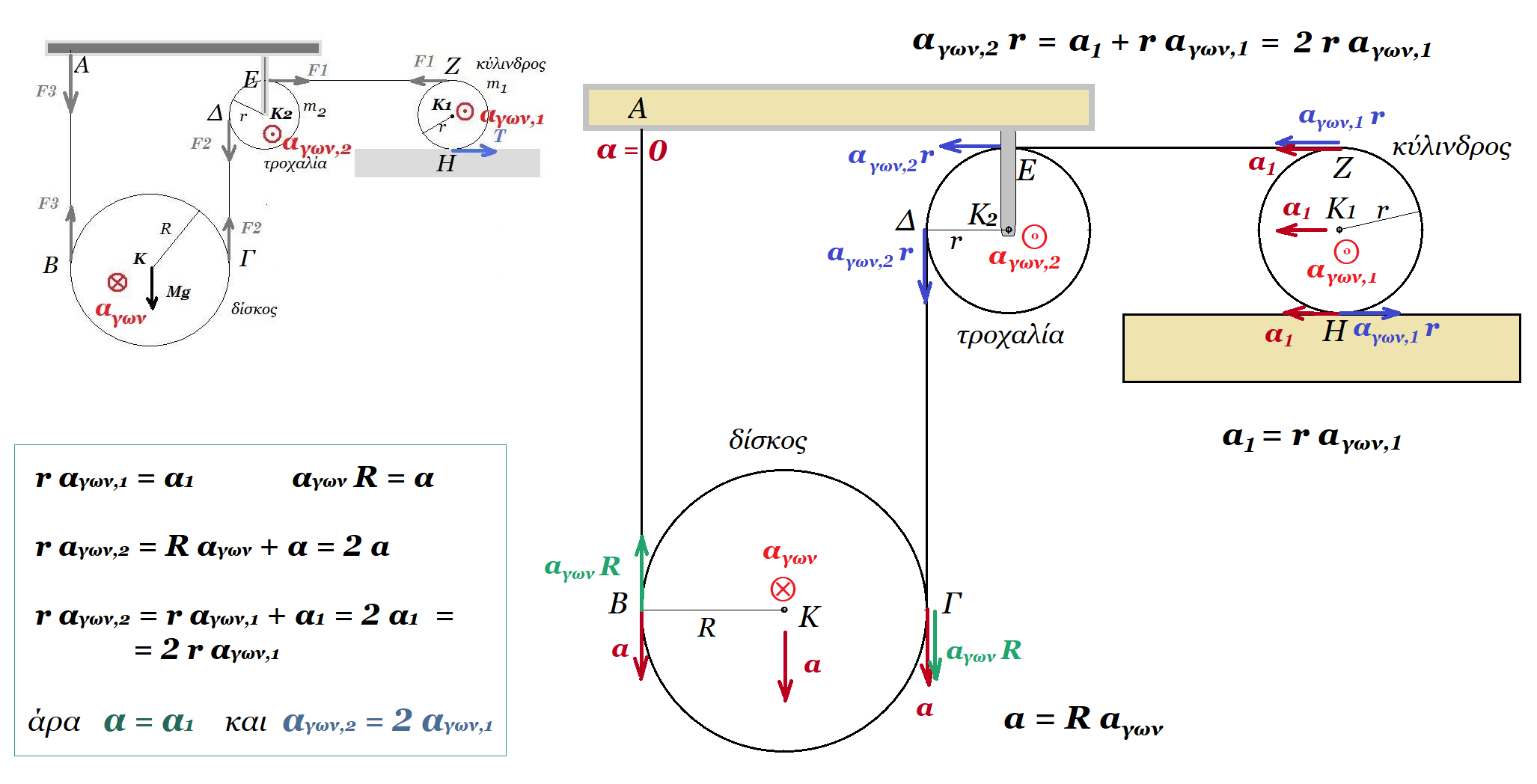
Η διάταξη του σχήματος είναι σε ισορροπία. Δείξτε ότι ο δίσκος δέχεται δύναμη στατικής τριβής μέτρου 10 Ν. Υπολογίστε την δύναμη που ασκείται στην τροχαλία στο κέντρο της Κ.
Την χρονική στιγμή t0 = 0 κόβουμε το νήμα που συνδέει τον δίσκο με το τοίχωμα, οπότε ο δίσκος κυλίεται χωρίς να ολισθαίνει, η τροχαλία στρέφεται περί το κέντρο της Κ και το σώμα Σ κινείται κατακόρυφα προς τα κάτω με επιτάχυνση αΣ = 3 m/s2.
Υπολογίστε την γωνιακή επιτάχυνση του δίσκου και την γωνιακή επιτάχυνση της τροχαλίας.
Βρείτε τις δυνάμεις που ασκούνται.
Αν το σώμα Σ κατέρχεται διανύοντας απόσταση y = 24 m πόση είναι η διανυόμενη απόσταση xcm του κέντρου μάζας του δίσκου;
r = 0,4 m, R = 0,8 m, m = 4 kg, Μτρ = 8 kg, Μδ = 8 kg

ισορροπία σώματος Σ : Τ1 = m g = 4 kg 10 m/s2 => T1 = 40 N
τροχαλία Στ(Κ) = 0 => Τ1 r = T2 r => T2 = T1 = 40 N
δίσκος Στ(Α) = 0 => Τ2 (R + r) = T3 2R => 40N (0,8m + 0,4m) = T3 2 0,8m => T3 = 30 N
ΣFx = 0 => T2 - T3 - Α = 0 => Α = T2 - T3 = 40N - 30N => Α = 10 N
τροχαλία ΣFx = 0 => Fx,K - T2 = 0 => Fx,K = T2 = 40 N
ΣFy = 0 => Fy,K - Mτρ g - T1 = 0 => Fy,K = 8 10 + 40 => Fy,K = 120 N
εφθ = Fy,K / Fx,K = 120N / 40Ν => εφθ = 3
FK2 = Fx,K2 + Fy,K2 = 402 + 1202 = 10 402 => FK = 40√10 N
aΣ = 3 m/s2 αΣ = r αγων,τρ = (r + R) αγων,δ = (r + R) acm / R => acm = αΣ R / (r + R)
αcm = 2 m/s2
αΣ = r αγων,τρ => αγων,τρ = αΣ / r = 3 m/s2 / 0,4 m => αγων,τρ = 15/2 rad/s2
acm = αγων,δ R => αγων,δ = acm / R = 2 m/s2 / 0,8 m => αγων,δ = 5/2 rad/s2
m g - Τ1 = m aΣ => 40 - Τ1 = 4 3 => Τ1 = 28 Ν
Τ1 - T2 = ½ Μτρ α => 28 - T2 = ½ 8 3 => T2 = 16 Ν
Τ2 - Α = Mδ acm => 16 - Α = 8 2 => Α = 0 τριβή
y = ½ α t2 => 24 m = ½ 3 t2 => t = 4 s
xcm = ½ αcm t2 = ½ 2 42 = 16 m
y / xcm = v / vcm = a / acm = 3/2 => y / xcm = 3/2 => 24 m / xcm = 3/2 => xcm = 16 m

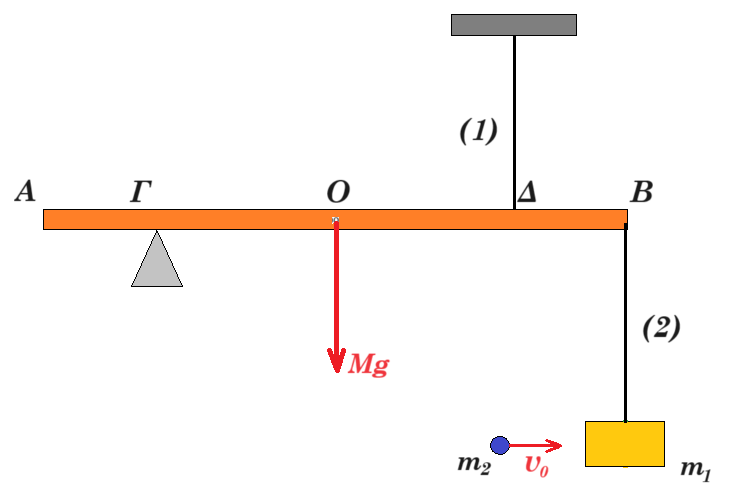
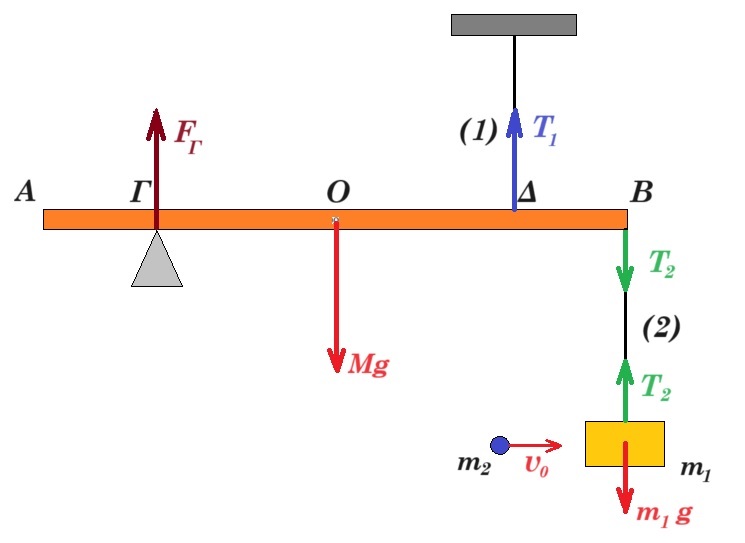
Η ομογενής ράβδος ΑΒ, μήκους 5m και βάρους 200Ν ισορροπεί σε οριζόντια θέση, ενώ στηρίζεται σε τρίποδο στο σημείο Γ, όπου (ΑΓ)=1m και κρέμεται στο άκρο Δ κατακόρυφου νήματος (1), όπου (ΔΒ)=1m. Μια πλάκα μάζας m1=1,8kg κρέμεται στο άκρο του νήματος (2) μήκους 2m, το άλλο άκρο του οποίου έχει δεθεί στο άκρο Β της ράβδου.
i) Να υπολογιστεί η δύναμη που δέχεται η ράβδος από το τρίποδο, κατά την παραπάνω ισορροπία.
Σε μια στιγμή μια σφαίρα μάζας m2=0,2kg, η οποία κινείται οριζόντια με ταχύτητα υ0=40m/s σφηνώνεται στην πλάκα, δημιουργώντας ένα συσσωμάτωμα Σ, το οποίο θεωρούμε υλικό σημείο αμελητέων διαστάσεων.
ii) Να υπολογιστεί η ορμή και η στροφορμή, ως προς το άκρο Β της ράβδου, του συσσωματώματος Σ, αμέσως μετά την κρούση.
iii) Να υπολογιστεί η τάση του νήματος (1), καθώς και ο ρυθμός μεταβολής της στροφορμής του Σ ως προς το Β, αμέσως μετά την κρούση,
Μετά από λίγο το σώμα Σ φτάνει σε μια θέση Ε, με μηδενική ταχύτητα, ενώ η ράβδος διαρκώς ισορροπεί. Για την στιγμή αυτή:
iv) Να υπολογιστεί η στροφορμή και ο ρυθμός μεταβολής της στροφορμής του Σ, ως προς το άκρο Β της ράβδου.
v) Να βρεθεί η οριζόντια και η κατακόρυφη συνιστώσα της δύναμης που ασκεί το τρίποδο στην ράβδο.
Δίνεται g=10m/s2.
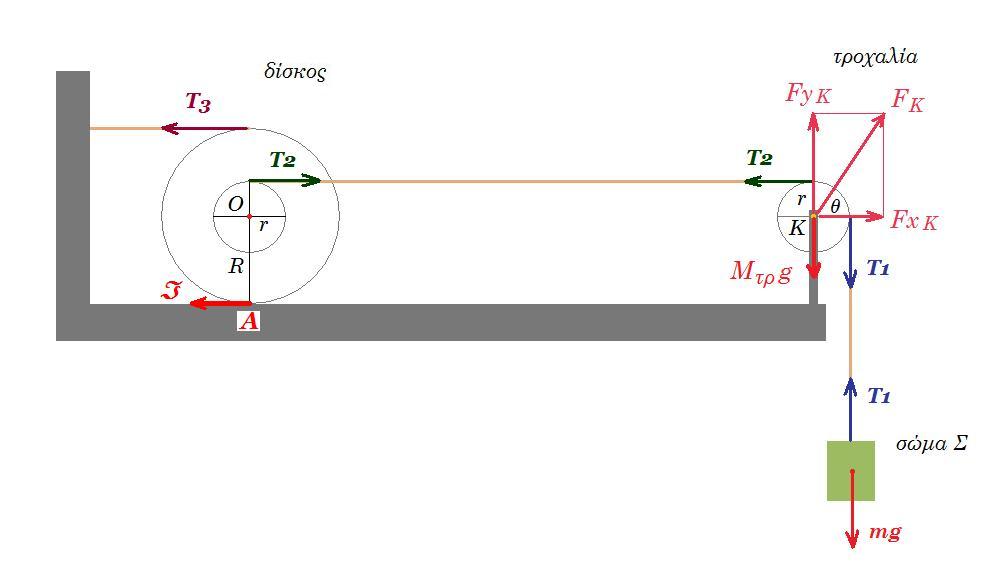
Η διάταξη του σχήματος είναι σε ισορροπία. Δείξτε ότι ο δίσκος δέχεται δύναμη στατικής τριβής μέτρου 10 Ν και υπολογίστε την δύναμη που ασκείται στην τροχαλία στο κέντρο της Κ.
Την χρονική στιγμή t0 = 0 κόβουμε το νήμα που συνδέει τον δίσκο με το τοίχωμα, οπότε ο δίσκος κυλίεται χωρίς να ολισθαίνει, η τροχαλία στρέφεται περί το κέντρο της Κ και το σώμα Σ κινείται κατακόρυφα προς τα κάτω με επιτάχυνση αΣ = 3 m/s2.
Υπολογίστε την γωνιακή επιτάχυνση του δίσκου και την γωνιακή επιτάχυνση της τροχαλίας.
Βρείτε τις δυνάμεις που ασκούνται.
Αν το σώμα Σ κατέρχεται διανύοντας απόσταση y = 24 m πόση είναι η διανυόμενη απόσταση xcm του κέντρου μάζας του δίσκου;
Πόση είναι η κινητική ενέργεια και ο ρυθμός μεταβολής της κινητικής ενέργειας του δίσκου εκείνη την χρονική στιγμή;
r = 0,4 m, R = 0,8 m, m = 4 kg, Μτρ = 8 kg, Μδ = 8 kg
α = r αγων,τρ
αγων,τρ r = αγων,δ (R + r)
acm = αγων,δ R
a = acm (R + r) / R => a = acm (0,8 + 0,4) / 0,8 => a = 3/2 acm
σώμα Σ : ΣF = m a => m g - Τ1 = m a
τροχαλία : Στ(Κ) = Iτρ(Κ) αγων,τρ => Τ1 r - T2 r = Iτρ(Κ) αγων,τρ =>
=> Τ1 r - T2 r = ½ Μτρ r2 αγων,τρ => Τ1 - T2 = ½ Μτρ r αγων,τρ = ½ Μτρ α
δίσκος : ΣF = Mδ acm => Τ2 - Α = Mδ acm
Στ(Ο) = Iδ(Ο) αγων,δ => Τ2 r + Α R = ½ Μδ R2 αγων,δ => Τ2 r/R + Α = ½ Μδ acm => Τ2 / 2 + Α = ½ Μδ acm
m g - Τ1 = m a (1)
Τ1 - T2 = ½ Μτρ α (2)
Τ2 - Α = Mδ acm (3)
Τ2 / 2 + Α = ½ Μδ acm (4) (3) + (4) => 3/2 T2 = 3/2 Μδ acm => T2 = Μδ acm (5)
(1) + (2) + (5) => m g - Τ1 + Τ1 - T2 + T2 = m a + ½ Μτρ α + Μδ acm
=> m g = m 3/2 acm + ½ Μτρ 3/2 αcm + Μδ acm
=> m g = ( 3/2 m + 3/4 Μτρ + Μδ ) acm
=> 4 10 = ( 3/2 4 + 3/4 8 + 8 ) acm
=> 4 10 = ( 6 + 6 + 8 ) acm => acm = 2 m/s2 α = 3/2 2 = 3 m/s2
α = r αγων,τρ => αγων,τρ = α / r = 3 m/s2 / 0,4 m => αγων,τρ = 15/2 rad/s2
acm = αγων,δ R => αγων,δ = acm / R = 2 m/s2 / 0,8 m => αγων,δ = 5/2 rad/s2
m g - Τ1 = m a => 40 - Τ1 = 4 3 => Τ1 = 28 Ν
Τ1 - T2 = ½ Μτρ α => 28 - T2 = ½ 8 3 => T2 = 16 Ν
Τ2 - Α = Mδ acm => 16 - Α = 8 2 => Α = 0
y = ½ α t2 => 24 m = ½ 3 t2 => t = 4 s
xcm = ½ αcm t2 = ½ 2 42 = 16 m
y / xcm = v / vcm = a / acm = 3/2 => y / xcm = 3/2 => 24 m / xcm = 3/2 => xcm = 16 m
ωδ = αγων,δ t = 5/2 4 = 10 rad/s ωτρ = αγων,τρ t = 15/2 4 = 30 rad/s
Kδ = ½ I(O) ωδ2 + ½ Mδ υcm2 = ½ ½ Μδ R2 ωδ2 + ½ Mδ υcm2 =
= 3/4 Μδ R2 ωδ2 = 3/4 8 0,82 102 = 384 J κινητική ενέργεια δίσκου
dKδ /dt = 3/2 Μδ R2 ωδ αγων,δ = 3/2 8 0,82 10 5/2 = 192 J/s
Kτρ = ½ I(Κ) ωτρ2 = ½ ½ Μτρ r2 ωτρ2 = 1/4 8 0,42 302 = 288 J κινητική ενέργεια τροχαλίας
dKτρ /dt = I(Κ) ωτρ αγων,τρ = ½ Μτρ r2 ωτρ αγων,τρ = ½ 8 0,42 30 15/2 = 144 J/s
m g y = 4 10 24 = 960 J δυναμική ενέργεια σώματος Σ
½ m v2 = ½ 4 122 = 288 J κινητική ενέργεια σώματος Σ
960 J = 288 J + 384 J + 288 J 480 J/s = 144 J/s + 192 J/s + 144 J/s
m g y = ½ m v2 + Kδ + Kτρ m g v = m v a + dKδ /dt + dKτρ /dt



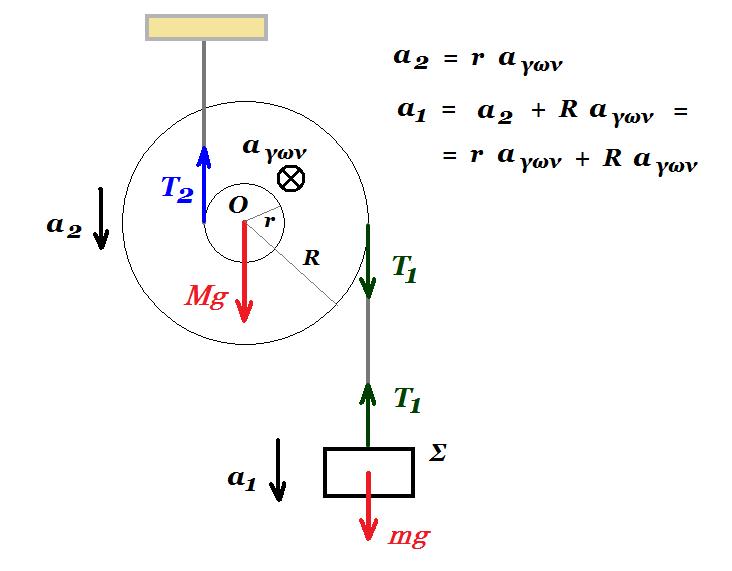
Θέμα 17.
Στο σύστημα που φαίνεται στο σχήμα η μικρή τροχαλία Κ2 είναι μάζας m2=1kg, ακτίνας r και το αβαρές σχοινί συνδέει τον κύλινδρο, Κ1, μάζας m1=8kg, ακτίνας r με το δίσκο, Κ, μάζας Μ=4kg και ακτίνας R. O κύλινδρος κυλίεται χωρίς να ολισθαίνει καθώς το τυλιγμένο σε αυτόν
νήμα ξετυλίγεται . Αν αφήσουμε το σύστημα ελεύθερο τη χρονική στιγμή t0=0, να υπολογιστούν:
Α. η επιτάχυνση α1 του κέντρου μάζας Κ1 του κυλίνδρου εάν ο δίσκος κατέρχεται με επιτάχυνση α = 2 m/s2
Β. η πτώση του κέντρου μάζας του δίσκου, Κ και η μετατόπιση του κέντρου μάζας του κυλίνδρου, Κ1 τη χρονική στιγμή t=2s.
Δ. Το ποσοστό της δυναμικής ενέργειας του δίσκου (Κ) που μετατράπηκε σε κινητικές ενέργειες του δίσκου, της τροχαλίας και του κυλίνδρου, μέχρι τη χρονική στιγμή t=2s.
Ε. Ο ρυθμός μεταβολής κινητικής ενέργειας του κυλίνδρου τη χρονική στιγμή t=2s.

(Α) r αγων,1 = α1 r αγων,2 = r αγων,1 + α1 = 2 α1
α = αγων R r aγων,2 = R αγων + α = 2 a άρα α1 = α = 2 m/s2
(B) y = ½ a t2 = ½ 2 22 = 4 m x1 = ½ a1 t2 = ½ 2 22 = 4 m

για τον κύλινδρο :
Στ(Κ1) = Ι(Κ1) αγων,1 => ( F1 + T ) r = ½ m1 r2 aγων,1 => F1 + T = ½ m1 a1
ΣF = m1 a1 => F1 - T = m1 a1 οπότε F1 = 3/4 m1 a1
και T = F1 - m1 a1 = 3/4 m1 a1 - m1 a1 => T = - m1 a1 /4 η Τ είναι ομόρροπη της F1
για την τροχαλία :
Στ(Κ2) = Ι(Κ2) αγων,2 => ( F2 - F1 ) r = ½ m2 r2 aγων,2 => F2 - F1 = ½ m2 r aγων,2 = ½ m2 2a1 = m2 a1
=> F2 - F1 = m2 a1 => F2 = ( 3/4 m1 + m2 ) a1
για τον δίσκο :
Στ(Κ) = Ι(Κ) αγων => (F3 - F2 ) R = ½ Μ R2 aγων => F3 - F2 = ½ Μ a = ½ M a1
ΣF = Μ a => Mg - F2 - F3 = M a = M a1
προσθέτω κατά μέλη θα φύγει η F3 : Mg - 2 F2 = M 3/2 a1 => Mg - 2 ( 3/4 m1 + m2 ) a1 = M 3/2 a1 => Mg = ( 3/2 m1 + 2 m2 + 3/2 M ) a1 => α1 = 40 / ( 12 + 2 + 6 ) = 40 / 20 => α1 = 2 m/s2 = α
(Β) οπότε F1 = 3/4 m1 a1 = 3/4 8 2 => F1 = 12 Ν και Τ = m1 a1 /4 = 8 2 /4 => Τ = 4 Ν
F2 = ( 3/4 m1 + m2 ) a1 = ( 3/4 8 + 1 ) 2 => F2 = 14 Ν
F3 - F2 = ½ Μ a = ½ M a1 => F3 - 14 = ½ 4 2 => F3 = 18 Ν
(Γ) y = ½ a t2 = ½ 2 22 = 4 m x1 = ½ a1 t2 = ½ 2 22 = 4 m
(Δ) vK = a t = 2 2 = 4 m/s vK1 = a1 t = 2 2 = 4 m/s ωK2 = αγων,2 . t = 2 α1 / r . t
M g y = ½ Μ υΚ2 + ½ ΙΚ ωΚ2 + ½ m1 υΚ12 + ½ ΙΚ1 ωΚ12 + ½ ΙΚ2 ωΚ22
M g y = ½ Μ υΚ2 + ½ ½ M R2 ωΚ2 + ½ m1 υΚ12 + ½ ½ m1 r2 ωΚ12 + ½ ½ m2 r2 (2 α1/r . t )2
M g y = 3/4 Μ υΚ2 + 3/4 m1 υΚ12 + ½ ½ m2 r2 4 α12/r2 t2
4 10 4 = 3/4 4 42 + 3/4 8 42 + ½ ½ 1 4 22 22
160 = 48 + 96 + 16
ποσοστά κύλινδρος Κ1 : 96/160 60% τροχαλία Κ2 : 16/160 10% δίσκος Κ : 48/160 30%
(Ε) dK1/dt = m1 υΚ1 a1 + ΙΚ1 ωΚ1 aγων,1 = m1 υΚ1 a1 + ½ m1 r2 ωΚ1 aγων,1 =
= m1 υΚ1 a1 + ½ m1 υΚ1 a1 = 3/2 m1 υΚ1 a1 = 3/2 8 4 2 = 96 J/s
aλλιώς Κ1 = 3/4 m1 υΚ12 οπότε dK1/dt = 3/2 m1 υΚ1 a1 = 3/2 8 4 2 = 96 J/s
παρατηρούμε ότι :
το έργο της F1 : F1 x1 = 12N 4m = 48 J το έργο της Τ : Τ x1 = 4N 4m = 16 J
F1 x1 + T x1 = 48 J + 16 J = 64 J = ½ 8 42 = ½ m1 υΚ12
F1 x1 - T x1 = 48 J - 16 J = 32 J = ½ ½ 8 42 = ½ ΙΚ1 ωΚ12
Ομογενής, άκαμπτη και μικρού πάχους σανίδα ΑΒ μάζας Μ = 2kg και μήκους l = 4m ισορροπεί σε πλάγια θέση με τη βοήθεια υποστηρίγματος, το οποίο έχουμε στερεώσει σε λείο οριζόντιο δάπεδο. Η σανίδα ακουμπά με το άκρο της Α στο λείο δάπεδο σχηματίζοντας γωνία φ = 30° με αυτό. Η σανίδα συνδέεται με την κορυφή του υποστηρίγματος με άρθρωση σε σημείο της Γ, το οποίο απέχει από το άκρο της Β απόσταση (ΒΓ) = 1,5 m. Η σανίδα μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από το σημείο Γ (κάθετος στο επίπεδο του σχήματος).
Ομογενής κύλινδρος μάζας ΜΚ = 2 kg και ακτίνας RΚ βρίσκεται σε επαφή με τη σανίδα στο σημείο Δ, το οποίο απέχει από το Γ απόσταση (ΓΔ) = 0,2 m.
Στο μέσο της επιφάνειας του κυλίνδρου, που φέρει ένα λεπτό αυλάκι, έχουμε τυλίξει πολλές φορές λεπτό, αβαρές και μη εκτατό νήμα, στο άλλο άκρο του οποίου έχουμε δέσει σώμα Σ μικρών διαστάσεων μάζας ΜΣ = 2 kg.
Το νήμα περνάει από το αυλάκι ομογενούς τροχαλίας μάζας ΜΤ = 2 kg και ακτίνας RΤ, την οποία έχουμε στερεώσει σε ακλόνητο σημείο. Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο μάζας της και είναι κάθετος στο επίπεδο της τροχαλίας. Το τμήμα του νήματος που συνδέει τον κύλινδρο με την τροχαλία έχει διεύθυνση παράλληλη με τη σανίδα.
Αρχικά ασκούμε δύναμη F στο κέντρο μάζας του κυλίνδρου με διεύθυνση παράλληλη προς την διεύθυνση ΑΒ, ώστε το σύστημα κύλινδρος -τροχαλία-σώμα να ισορροπεί, όπως φαίνεται στο σχήμα .
Δ1. Να υπολογίσετε το μέτρο της δύναμης F.
Τη χρονική στιγμή t = 0 καταργούμε ακαριαία τη δύναμη και το σώμα Σ αρχίζει να κατέρχεται κατακόρυφα, ενώ ο κύλινδρος αρχίζει να ανέρχεται στη σανίδα εκτελώντας κύλιση χωρίς ολίσθηση και το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας.
Δ2. Να αποδείξετε ότι το μέτρο της επιτάχυνσης με την οποία κατέρχεται το σώμα Σ είναι ίσο με 4 m / s2 και να υπολογίσετε το μέτρο της επιτάχυνσης του κέντρου μάζας του κυλίνδρου.
Τη χρονική στιγμή t1 = 0,5 s κόβουμε ακαριαία το νήμα στο σημείο που εφάπτεται με τον κύλινδρο και στο σημείο πρόσδεσης με το σώμα Σ. Μετά το κόψιμο του νήματος, αυτό δεν εμποδίζει την κίνηση του κυλίνδρου και του σώματος. Ο κύλινδρος συνεχίζει την κίνησή του εκτελώντας κύλιση χωρίς ολίσθηση.
Δ3. Να υπολογίσετε τη χρονική στιγμή t2 στην οποία ο κύλινδρος σταματά στιγμιαία να κινείται πάνω στη σανίδα.
Δ4. Να υπολογίσετε το συνολικό διάστημα που διάνυσε ο κύλινδρος από τη χρονική στιγμή t = 0 έως τη χρονική στιγμή t2.
Δ5. Να δείξετε ότι κατά τη διάρκεια της ανόδου του κυλίνδρου πάνω στη σανίδα, από τη χρονική στιγμή t = 0 έως τη χρονική στιγμή t2, που ο κύλινδρος σταματά στιγμιαία, η σανίδα δεν ανατρέπεται.
ισορροπία σώματος Σ : m g = T1 => Τ1 = 20 Ν
ισορροπία τροχαλίας : T1 Rτρ = T2 Rτρ => T1 = T2 = 20 Ν
ισορροπία κυλίνδρου : Tστ Rκ = T2 Rκ => Tστ = T2 = 20 Ν
Μκ g ημ30° + F = T2 + Tστ => 2 10 ½ + F = 20 + 20 => F = 30 Ν
κατακόρυφη κίνηση σώματος Σ : ΣF = m aΣ => m g - T1 = m aΣ (1) αΣ = αγων,τρ Rτρ
περιστροφή τροχαλίας : T1 Rτρ - T2 Rτρ = Ιτρ αγων,τρ => T1 Rτρ - T2 Rτρ = ½ Μτρ Rτρ2 αγων,τρ =>
=> T1 - T2 = ½ Μτρ Rτρ αγων,τρ = ½ Μτρ αΣ (2)
κίνηση κυλίνδρου : Tστ Rκ + T2 Rκ = Ικ αγων,κ => Tστ Rκ + T2 Rκ = ½ Μκ Rκ2 αγων,κ =>
=> Tστ + T2 = ½ Μκ Rκ αγων,κ = ½ Μκ ακ (3)
T2 - Tστ - Μκ g ημ30° = Μκ ακ (4) αΣ = 2 ακ
(3) + (4) => 2 T2 - Μκ g ημ30° = 3/2 Μκ ακ => T2 - 1/4 Μκ g = 3/4 Μκ ακ (5)
(1) + (2) + (5) => m g - T1 + T1 - T2 + T2 - 1/4 Μκ g = m aΣ + ½ Μτρ αΣ + 3/4 Μκ ακ =>
=> 20 - 1/4 20 = 2 aΣ + ½ 2 αΣ + 3/4 2 ακ => 15 = 2 aΣ + αΣ + 3/4 αΣ => αΣ = 4 m/s2 άρα ακ = 2 m/s2
t1 = 0,5 s χκ = ½ ακ t1 = ½ 2 0,52 = 0,25 m υκ = ακ t1 = 2 0,5 = 1 m/s
κίνηση κυλίνδρου : Tστ Rκ = Ικ αγων,κ => Tστ Rκ = ½ Μκ Rκ2 αγων,κ =>
=> Tστ = ½ Μκ Rκ αγων,κ = ½ Μκ ακ (6)
- Tστ - Μκ g ημ30° = Μκ ακ (7) (6) + (7) => - Μκ g ημ30° = 3/2 Μκ ακ => ακ = - 10/3 m/s2
υκ = 1 m/s - 10/3 m/s2 t = 0 => t = 0,3 s t2 = 0,5 s + 0,3 s = 0,8 s
χ = 1 m/s 0,3 s - ½ 10/3 m/s2 0,09 s2 = 0,15 m
ο κύλινδρος έχει προχωρήσει 0,25 m + 0,15 m = 0,4 m = (ΔΕ)
(ΓΕ) = (ΔΕ) - (ΓΔ) = 0,4 - 0,2 = 0,2 m
ροπές ως προς Γ : Μ g (ΓΚ) συν30° - Μκ g (ΓΕ) συν30° = 2 10 0,5 συν30° - 2 10 0,2 συν30° > 0 υπερισχύει η ροπή του βάρους της σανίδας οπότε δεν ανατρέπεται
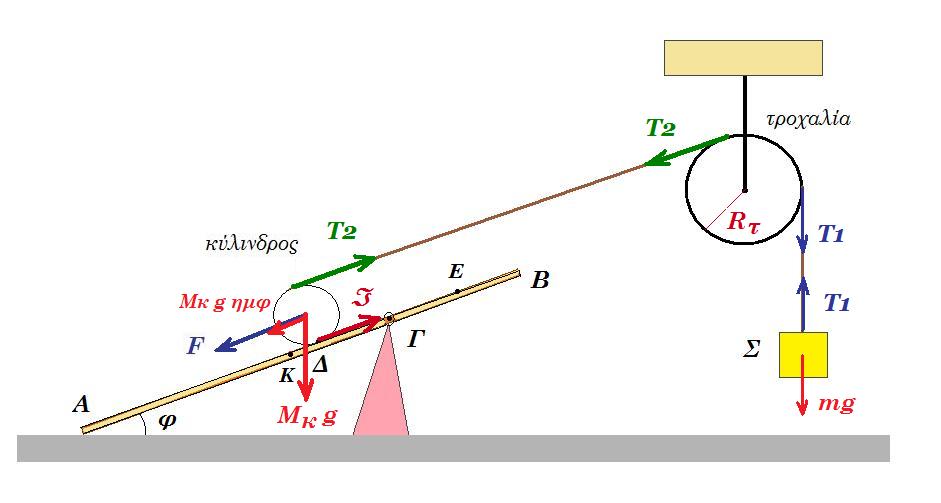
Θέμα 12. 2017
Μία ομογενής άκαμπτη ράβδος ΑΓ σταθερής διατομής έχει μάζα Μ=4Kg. Η ράβδος ισορροπεί σε οριζόντια θέση και το άκρο της Α συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Το άλλο άκρο Γ της ράβδου συνδέεται μέσω αβαρούς μη εκτατού νήματος ΓΔ με τον κατακόρυφο τοίχο. Το νήμα σχηματίζει με τη ράβδο γωνία φ. Γύρω από ένα λεπτό ομογενή δίσκο κέντρου Κ, μάζας m=2kg και ακτίνας R=0,1m είναι τυλιγμένο πολλές φορές ένα λεπτό μη εκτατό αβαρές νήμα. Το ελεύθερο άκρο του νήματος έχει στερεωθεί στο άκρο Γ της ράβδου ΑΓ, όπως φαίνεται στο σχήμα
Τη χρονική στιγμή t0=0 ο δίσκος αφήνεται να κινηθεί και το νήμα ξετυλίγεται χωρίς να ολισθαίνει.
Δ1. Να υπολογίσετε το μέτρο της επιτάχυνσης του κέντρου μάζας του δίσκου, καθώς αυτός κατέρχεται.
Δ2. Να υπολογίσετε το μέτρο της δύναμης που δέχεται η ράβδος ΑΓ στο άκρο της Γ από το νήμα ΓΔ, όταν ο δίσκος κατέρχεται καθώς και την δύναμη που δέχεται η ράβδος ΑΓ στο άκρο της Α από την άρθρωση.
Τη χρονική στιγμή που το κέντρο μάζας Κ του δίσκου έχει κατέλθει κατακόρυφα κατά h1=0,3m το νήμα που συνδέει το δίσκο με τη ράβδο κόβεται.
Δ3. Να υπολογίσετε το μέτρο της στροφορμής του δίσκου ως προς τον άξονα περιστροφής του, μετά από χρονικό διάστημα Δt από τη στιγμή που κόπηκε το νήμα.
Δ4. Να υπολογίσετε το λόγο της κινητικής ενέργειας λόγω περιστροφικής κίνησης προς την κινητική ενέργεια λόγω μεταφορικής κίνησης του δίσκου μετά από χρονικό διάστημα Δt ́=0,1s από τη στιγμή που κόπηκε το νήμα.
Δίνονται: η επιτάχυνση της βαρύτητας g = 10 m/s2 ημφ = 0,8 και συνφ = 0,6 ο άξονας περιστροφής του δίσκου παραμένει συνεχώς οριζόντιος και κινείται σε κατακόρυφη τροχιά σε όλη τη διάρκεια της κίνησης του, ο δίσκος δεν φτάνει στο έδαφος στη διάρκεια του φαινομένου.
Δ1.
ροπές ως προς Κ : T1 R = I αγων => T1 R = ½ m R2 αγων => T1 = ½ m R αγων = ½ m α
mg - T1 = m a => mg = ½ m α + m a = 3/2 m α => a = 2g/3 => a = 20/3 m/s2
αγων = α / R = 20/3 / 0,1 => αγων = 200/3 rad/s2 T1 = ½ m α = ½ 2 20/3 => Τ1 = 20/3 N
Δ2.
ροπές ως προς Α : M g l/2 + T1 l - T2 ημφ l = 0 => 4 10 /2 + 20/3 - T2 0,8 = 0 =>
=> 20 + 20/3 = T2 0,8 => T2 = 80/3 / 0,8 => T2 = 100/3 Ν
ΣFx = 0 => FAx = T2x = T2 συνφ => FAx = 100/3 0,6 = 20 Ν
ΣFy = 0 => FAy + T2y = T1 + Mg =>
=> FAy = - T2 ημφ + T1 + Mg = - 100/3 0,8 + 20/3 + 40 => FAy = 20 Ν
FA2 = FAx2 + FAy2 = 202 + 202 => FA = 20 2½ Ν
Δ3.
h = ½ a t2 => 0,3 = ½ 20/3 t2 => t = 0,3 s τότε υ = α t = 20/3 0,3 = 2 m/s
ω = αγων t = 200/3 0,3 = 20 rad/s = σταθερή διότι από τη στιγμή που κόβεται το νήμα δεν δέχεται ροπή ο δίσκος Τ1 = 0
L = I ω = ½ m R2 ω = ½ 2 0,12 20 => L = 0,2 kg m2 / s
Δ4.
ΣFy = m α => m g = m a => a = g = 10 m/s2 τότε υ = v0 + α t = 2 m/s + 10 m/s2 0,1s = 3 m/s
Kμεταφορική = ½ m υ2 = ½ 2 32 = 9 J
Kπεριστροφική = ½ Ι ω2 = ½ 0,01 202 = 2 J

Θέμα 13. 2015 εκτός ροπή αδράνειας
Από το εσωτερικό άκρο Α ενός ημισφαιρίου ακτίνας R= 1,6m αφήνεται να κυλήσει μία συμπαγής μικρή σφαίρα μάζας m=1,4kg και ακτίνας r = R/8. Το ημισφαίριο είναι βυθισμένο στο έδαφος, όπως φαίνεται στο σχήμα και η κίνηση της σφαίρας γίνεται χωρίς ολίσθηση.
Δ1. Να εκφράσετε τη στατική τριβή T που ασκείται στη σφαίρα σε συνάρτηση με το συνημίτονο της γωνίας φ που σχηματίζει η ακτίνα ΟΓ του ημισφαιρίου με την ευθεία ΑΕ της επιφάνειας του εδάφους.
Δ2. Να υπολογίσετε την κάθετη δύναμη που ασκεί η ημισφαιρική επιφάνεια στη σφαίρα όταν αυτή βρίσκεται στο σημείο Γ όπου φ = 30° .
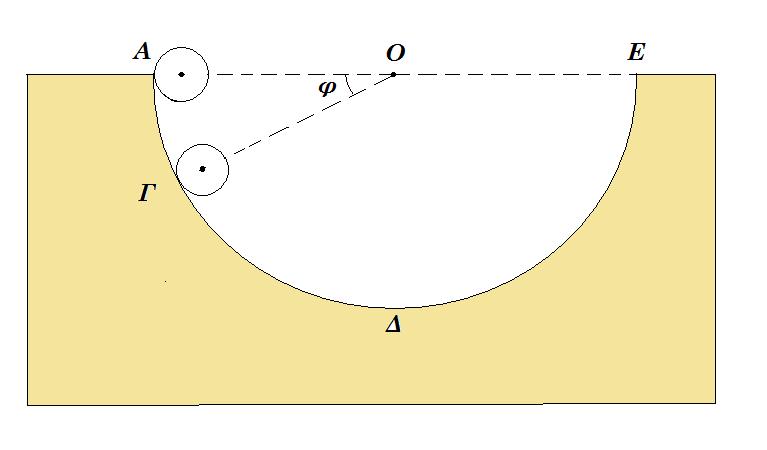 Μια άλλη σφαίρα, όμοια με την προηγούμενη, εκτοξεύεται από το κατώτατο σημείο Δ του ημισφαιρίου με ταχύτητα υ = 6m/s και κυλίεται χωρίς ολίσθηση στο εσωτερικό του με κατεύθυνση το άκρο Ε.
Μια άλλη σφαίρα, όμοια με την προηγούμενη, εκτοξεύεται από το κατώτατο σημείο Δ του ημισφαιρίου με ταχύτητα υ = 6m/s και κυλίεται χωρίς ολίσθηση στο εσωτερικό του με κατεύθυνση το άκρο Ε.
Δ3. Να υπολογίσετε το μέγιστο ύψος από την επιφάνεια του εδάφους που θα φτάσει η σφαίρα κατά την κίνησή της.
Δ4. Να υπολογίσετε το ρυθμό μεταβολής της κινητικής ενέργειας και το ρυθμό μεταβολής της στροφορμής της σφαίρας, αμέσως μόλις αυτή χάσει την επαφή με την επιφάνεια του ημισφαιρίου στο σημείο Ε.
Δ1.
Στ(Κ) = Ι(Κ) αγων => Τ r = 2/5 m r2 αγων => Τ = 2/5 m r αγων => Τ = 2/5 m α r αγων = a
ΣF = m a => m g συνφ - Τ = m a => m g συνφ = 2/5 m α + m a = 7/5 m α => 5/7 g συνφ = α
Τ = 2/7 m g συνφ = 2/7 1,4 10 συνφ => Τ = 4 συνφ
Δ2. διατήρηση ενέργειας Α ® Γ : m g h = ½ m v2 + ½ Ι(Κ) ω2 =>
=> m g (R - r)ημφ = ½ m v2 + ½ 2/5 m r2 ω2 =>
=> g (R - r)ημφ = ½ v2 + 1/5 v2 = 7/10 v2 => 10/7 g (R - r)ημφ = v2
ΣF = Fκ => Ν - m g ημφ = m υ2 / (R - r) => Ν = m g ημφ + m 10/7 g ημφ =>
=> Ν = 17/7 m g ημφ = 17/7 1,4 10 1/2 => Ν = 17 Ν
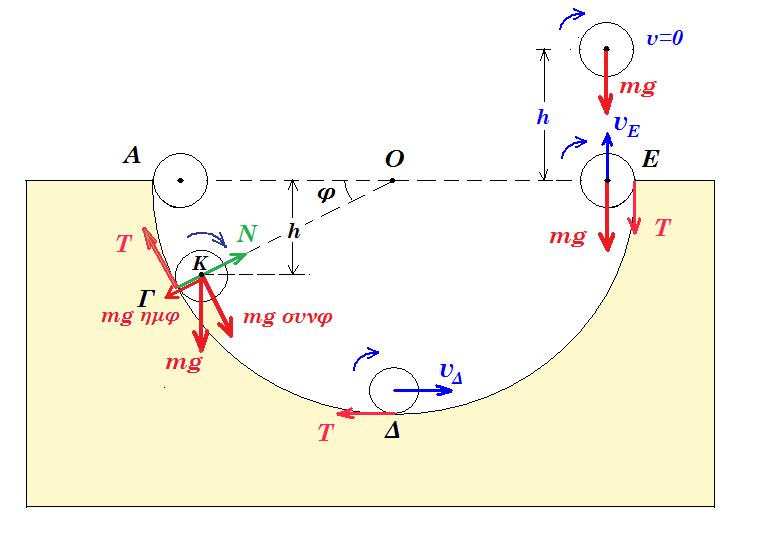
Δ3. διατήρηση ενέργειας Δ ® Ε : ½ m vΔ2 + ½ Ι(Κ) ω2 = m g (R - r) + ½ m vΕ2 + ½ Ι(Κ) ω2 =>
=> ½ m vΔ2 + ½ 2/5 m r2 ω2 = m g (R - R/8) + ½ m vΕ2 + ½ 2/5 m r2 ω2 =>
=> ½ vΔ2 + 1/5 vΔ2 = g 7/8 R + ½ vΕ2 + 1/5 vΕ2 =>
=> 7/10 vΔ2 = 7/8 R g + 7/10 vΕ2 => vΔ2 = 10/8 R g + vΕ2 =>
=> 36 - 5/4 1,6 10 = vΕ2 => vΕ2 = 36 - 20 = 16 => vΕ = 4m/s
στο σημείο Ε : ω = vΕ / r = 4 / 0,2 = 20 rad/s
όταν η σφαίρα εγκαταλήψει το ημικύκλιο στο σημείο Ε συνεχίζει να περιστρέφεται με την ίδια γωνιακή ταχύτητα ω = 20 rad/s διότι δεν ασκείται δύναμη που να δημιουργεί ροπή ( η σφαίρα είναι στον αέρα ενεργεί μόνο το βάρος της ) Στ(Κ) = 0
m g h + ½ Ι(Κ) ω2 = ½ m vΕ2 + ½ Ι(Κ) ω2 => m g h = ½ m vΕ2 =>
=> g h = ½ vΕ2 => h = ½ 16 / 10 => h = 0,8 m
Δ4. όταν η σφαίρα εγκαταλείπει το ημικύκλιο στο σημείο Ε
(dK / dt)μεταφορική = P = F . v = - mg vE = - 1,4 10 4 = - 56 J/s
(dK / dt)περιστροφική = Στ(Κ) . ω(Ε) = 0 . 20 rad/s = 0
ο ρυθμός μεταβολής της στροφορμής : dL/dt = Στ(Κ) = 0
Θέμα 14.
Σώμα μάζας m=1kg δεμένο στο ελεύθερο άκρο οριζόντιου και στερεωμένου ελατηρίου κάνει ΑΑΤ με μέγιστη κινητική ενέργεια K0=2J και πλάτος Α=0,2m. Τη χρονική στιγμή t0=0 το σώμα βρίσκεται στη θέση x=-0,2m. Τη στιγμή t1 που το σώμα m περνάει για πρώτη φορά από τη θέση ισορροπίας κινούμενο προς την πλευρά που το ελατήριο επιμηκύνεται κόβεται το ελατήριο και το σώμα συνεχίζει μόνο του πάνω στο λείο οριζόντιο επίπεδο.
Α. Να γραφεί η εξίσωση απομάκρυνσης των ΑΑΤ του σώματος και να υπολογιστούν η χρονική στιγμή t1 και η ταχύτητα του σώματος τη στιγμή που κόβεται τοελατήριο.
Το σώμα μετά συγκρούεται με το άκρο Δ, ράβδου μήκους d=1m, μάζας Μ=2kg το ένα άκρο της οποίας είναι στερεωμένο στο σημείο Ο, και μπορεί να στρέφεται χωρίς τριβές. Μετά την κρούση το σώμα m συνεχίζει την κίνησή του στην ίδια κατεύθυνση με ταχύτητα μέτρου ίσου με το μισό αυτής που είχε πριν την κρούση. Η κρούση διαρκεί χρόνο Δt=0,02s.
Να υπολογιστούν:
Β. Η ροπή τ που άσκησε το σώμα στη ράβδο κατά την κρούση, αν η ροπή θεωρηθεί σταθερή.
Γ. Η απώλεια μηχανικής ενέργειας του συστήματος, «σώμα - ράβδος» λόγω κρούσης.
Δ. Το μέτρο της δύναμης που ασκεί ο άξονας, Ο, στη ράβδο αμέσως μετά την κρούση.
Ε. Το συνημίτονο της γωνίας θ που σχηματίζει η ράβδος με την κατακόρυφο τη στιγμή που σταματάει στιγμιαία.

K0 = ½ k A2 => 2 J = ½ k (0,2m)2 => k = 100 N/m
k = m ω2 => 100 = 1 ω2 => ω = 10 rad/s T = 2π/ω = π/5 sec x(t) = 0,2 ημ(10t + 3π/2)
υ(t) = 2 συν(10t + 3π/2) α(t) = - 20 ημ(10t + 3π/2)
το ελατήριο κόβεται τη στιγμή που το σώμα περνά για 1η φορά από τη Θ.Ι. δηλαδή t = T/4 = π/20 sec η ταχύτητά του είναι η μέγιστη υ = 2 m/s
το επίπεδο είναι λείο διατήρηση στροφορμής : m v d = m v/2 d + I(O) ω =>
=> m v d = m v/2 d + 1/3 Μ d2 ω =>
=> 1 2 1 = 1 2/2 1 + 1/3 2 12 ω => ω = 1,5 rad/s
τ = dL/dt = ( Lμετά - Lπριν ) / dt = ( I(O) ω - 0 ) / dt = 1/3 Μ d2 ω / dt = 1/3 2 12 1,5 / 0,02 => τ = 50 Nm
Kπριν = ½ m v2 = ½ 1 22 = 2 J
Kμετά = ½ m (v/2)2 + ½ I(O) ω2 = ½ m (v/2)2 + ½ 1/3 Μ d2 ω2 =
= ½ 1 (2/2)2 + ½ 1/3 2 12 1,52 = ½ + 0,75 = 1,25 J
ΔΚ = Kμετά - Kπριν = 1,25 - 2 = - 0,75 J
ΣFy = Fκεντρομόλος => Ν - Μ g = M ω2 d/2 => Ν = Μ g + M ω2 d/2 =>
=> Ν = 2 10 + 2 1,52 1/2 => Ν = 22,25 Ν
διατήρηση ενέργειας : ½ 1/3 Μ d2 ω2 = Μ g d/2 ( 1 - συνθ ) => 1/3 d ω2 = g ( 1 - συνθ ) =>
=> 1 - d ω2 / 3g = συνθ => συνθ = 1 - 1 1,52 / 30 => συνθ = 0,925
Θέμα 15.
Στο σύστημα του σχήματος βλέπουμε τον ομογενή κύλινδρο κέντρου Ο, μάζας m1=6kg και ακτίνας ρ να ισορροπεί πάνω στο κεκλιμένο επίπεδο με τη βοήθεια νήματος ( παράλληλο στο κεκλιμένο επίπεδο ) το οποίο αφού περάσει από τροχαλία κέντρου Ζ ακτίνας b καταλήγει στο σημείο Δ της ομογενούς ράβδου ΑΓ που έχει μάζα m2. Η ράβδος στηρίζεται σε ακλόνητο σημείο μέσω άρθρωσης Α. Η απόσταση ΑΔ είναι d/3, όπου d το μήκος της ράβδου. Οι γωνίες φ έχουν ημφ=0,6 και συνφ=0,8. Στο κέντρο Ν της ράβδου έχει δεθεί νήμα που καταλήγει στο κέντρο ομογενούς αγωγού ΚΛ μάζας m=0,8kg η οποία ισορροπεί σε επαφή με δύο λείες κατακόρυφες αγώγιμες ράγες αμελητέας αντίστασης.
Α. Να υπολογιστεί η μάζα m2 της ράβδου αν όλο το σύστημα ισορροπεί.
Κόβουμε το νήμα ΝΠ και ο αγωγός ΚΛ, του σχήματος, με μήκος L=1m, αντίσταση r=1Ω απελευθερώνεται και κατεβαίνει τις ράγες χωρίς τριβές, ενώ το κάθετο μαγνητικό πεδίο έχει ένταση B=2Τ. Οι ράγες συνδέονται στο κάτω μέρος τους με αντιστάτη, αντίστασης R=3Ω. Από
τη στιγμή t0=0 που κόβεται το νήμα ο αγωγός ΚΛ δέχεται σταθερή κατακόρυφη δύναμη F=6N με φορά προς τα πάνω.
Β. Να δείξετε ότι ο αγωγός ΚΛ αποκτάει κάποια στιγμή οριακή ταχύτητα και να την υπολογίσετε
Γ. Αν από τη στιγμή που κόπηκε το νήμα και ξεκίνησε μέχρι να αποκτήσει οριακή ταχύτητα έπεσε
κατά y=1m να υπολογίσετε τη θερμότητα Joule που εκλύθηκε
σε κάθε αντιστάτη στο διάστημα αυτό.
Δ. Πόσο φορτίο μετακινήθηκε μέσα από τον αγωγό κατά την πτώση y=1m;
Ε. Μετά το κόψιμο του νήματος απελευθερώνεται και ο κύλινδρος και κατεβαίνει το κεκλιμένο
επίπεδο. Για ποιες τιμές του συντελεστή οριακής τριβής είναι δυνατή η κύλιση του κυλίνδρου χωρίς ολίσθηση.

(Α) ισορροπία ράβδου ΚΛ : m g = T3 => T3 = 0,8 10 = 8 Ν
ισορροπία ράβδου ΑΓ :
ροπές ως προς Α : Στ(Α) = 0 => m2 g d/2 συνφ + T3 d/2 συνφ - T2 d/3 ημφ = 0
ισορροπία τροχαλίας :
ροπές ως προς Ζ : Στ(Ζ) = 0 => Τ2 b = T1 b => Τ2 = T1
ισορροπία κυλίνδρου :
ροπές ως προς Ο : Στ(Ο) = 0 => Τ1 ρ = Tτριβ ρ => T1 = Tτριβ
ΣFx = 0 => m1 g ημφ - T1 - Tτριβ = 0 => 6 10 0,6 - T1 - T1 = 0 => Τ1 = 18 Ν
άρα Τ2 = T1 = 18 Ν
οπότε m2 g d/2 συνφ + T3 d/2 συνφ - T2 d/3 ημφ = 0 =>
=> m2 10 1/2 0,8 + 8 1/2 0,8 - 18 1/3 0,6 = 0 => m2 = (3,6 - 3,2) / 4 => m2 = 0,1 kg
(Β) τα ηλεκτρόνια της ράβδου δέχονται δύναμη Lorenz και μετακινούνται προς το άκρο Κ που φορτίζεται αρνητικά, αναπτύσσεται επαγωγική τάση στα άκρα Λ(+), Κ(-) της ράβδου Εεπαγ = Β l v
οπότε το κύκλωμα διαρρέεται με ρεύμα εντάσεως i = Εεπαγ / (R + r) = Β l v / (R + r)
στη ράβδο ασκείται δύναμη Laplace FL = B i l = Β2 l2 v / (R + r)
για την κίνηση της ράβδου έχουμε :
ΣF = m a => m g - FL - F = m a => m g - Β2 l2 v / (R + r) - F = m a
καθώς η ραβδος κατέρχεται αυξάνεται η ταχύτητα με συνέπεια να μειώνεται η επιτάχυνση έως ότου μηδενισθεί οπότε η ράβδος θα αποκτήσει σταθερή ταχύτητα ( οριακή )
α = 0 => m g - F = Β2 l2 v / (R + r) => υ = ( m g - F ) (R + r) / Β2 l2 => υ = ( 0,8 10 - 6 ) (3+1) / 4 1 = 2 m/s οριακή ταχύτητα
(Γ) m g y - F y - Q = ½ m v2 => Q = m g y - F y - ½ m v2 =>
=> Q = 0,8 10 1 - 6 1 - ½ 0,8 22 => Q = 8 - 6 - 1,6 = 0,4 J
Q(r) = i2 r t Q(R) = i2 R t Q(r) / Q(R) = r / R = 1/3
Q(r) + Q(R) = Q = 0,4 J άρα Q(r) = 0,1 J και Q(R) = 0,3 J
(Δ) q = ΔΦ / (r + R) = Β Α / (r + R) = B l y / (r + R) = 2 1 1 / 4 = 0,5 C
(E) Στ(Ο) = Ι(Ο) αγων => Ττριβ ρ = ½ m1 ρ2 αγων => Ττριβ = ½ m1 ρ αγων = ½ m1 a
ΣFx = m1 g ημφ - Ττριβ = m1 a => m1 g ημφ - ½ m1 a = m1 a => m1 g ημφ = 3/2 m1 a => α = 2/3 g ημφ = 2/3 10 0,6 = 4 m/s2
οπότε Ττριβ = ½ m1 a = ½ 0,8 4 = 1,6 Ν
ΣFy = 0 => m1 g συνφ = Ν => Ν = 0,8 10 0,8 = 6,4 Ν
ο συντελεστής τριβής κυλίσεως : μ = Τ / Ν = 1,6 / 6,4 = 0,25


Θέμα 16.
Τροχαλία μάζας Μ=2kg και ακτίνας R, είναι στερεωμένη, όπως φαίνεται στο σχήμα και μπορεί να στρέφεται γύρω από τον άξονά της. Από την τροχαλία διέρχεται νήμα στο ένα άκρο του οποίου δένεται νήμα στο ένα άκρο του οποίου δένεται σώμα μάζας m=4kg, ενώ το άλλο άκρο δένεται στο ελεύθερο άκρο ελατηρίου σταθεράς k=80Ν/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε ακλόνητο σημείο. Ανυψώνουμε το σώμα ως το σημείο Α, έτσι ώστε το ελατήριο να έχει το φυσικό του μήκος, ενώ το νήμα είναι τεντωμένο. Αφήνουμε το σώμα ελεύθερο.
A. Εξετάστε αν το σώμα μάζας m κάνει ΑΑΤ. Θετική φορά όπως το βάρος του σώματος.
B. Πόση είναι η επιτάχυνση του σώματος όταν η επιμήκυνση του ελατηρίου είναι x1=0,2m;
Γ. Πόση είναι η μέγιστη επιμήκυνση του ελατηρίου;
Δ. Πόση πρέπει να είναι η κατακόρυφη μετατόπιση του σώματος μέχρι το σώμα να αποκτήσει μέγιστη ταχύτητα.
E. Πόση είναι η μέγιστη ταχύτητα.
Z. Πόσο είναι ο ρυθμός μεταβολής της κινητικής ενέργειας του συστήματος «τροχαλία - σώμα», όταν η ταχύτητα του σώματος είναι υ=2m/s;
η ροπή αδράνειας της τροχαλίας : Ι(Ο) = ½ Μ R2 
(Α) ισορροπία σώματος : m g - T1 = 0
ισορροπία τροχαλίας : Στ(Ο) = 0 => T1 R - T2 R = 0 => T1 = T2
ελατήριο : Τ2 = Fελατ = k Δl m g = k Δl => Δl = 4 10 / 80 = 0,5 m αρχική επιμήκυνση του ελατηρίου όταν το σύστημα ισορροπεί
σώμα : ΣF = m g - T1 = m a (1)
τροχαλία : Στ(Ο) = Ι(Ο) αγων => T1 R - T2 R = ½ Μ R2 αγων =>
=> T1 - T2 = ½ Μ R αγων = ½ Μ α (2)
ελατήριο : Τ2 = Fελατ = k ( x + Δl ) (3)
(1) + (2) + (3) => m g = m a + ½ Μ α + k ( x + Δl ) =>
=> 0 = m a + ½ Μ α + k x =>
=> ( m + ½ Μ ) α = - k x => α = - k /( m + ½ Μ ) x => το σώμα εκτελεί ΑΑΤ με συχνότητα ω2 = k /( m + ½ Μ ) = 80 /( 4 + ½ 2 ) = 80 / 5 = 16 => ω = 4 rad/s
T = 2π/ω = 2π/4 = π/2 s
x(t) = 0,5 ημ(4t + 3π/2) υ(t) = 2 συν(4t + 3π/2) α(t) = -8 ημ(4t + 3π/2) ΣF(t) = m a(t) = -32 ημ(4t + 3π/2)
Fελατ(t)= k ( x + Δl ) = 80 { 0,5 ημ(4t + 3π/2) + 0,5 } = 40 + 40 ημ(4t + 3π/2)
(Β) επιμήκυνση ελατηρίου x1 = 0,2m => x + Δl = 0,2 => x + 0,5 = 0,2 => x = - 0,3 m
0,5 ημ(4t + 3π/2) = - 0,3 => ημ(4t + 3π/2) = - 0,6
α = - 8 ημ(4t + 3π/2) = - 8 ( - 0,6 ) => a = + 4,8 m/s2
(Γ) t = 0 Fελατ(t)= k ( x + Δl ) = 40 + 40 ημ(3π/2) = 40 + (- 40) = 0
t = T/2 = π/4 s Fελατ(t)= k ( x + Δl ) = 40 + 40 ημ(4 π/4 + 3π/2) = 40 + 40 ημ(π/2) = 40 + 40 = 80 Ν μέγιστη δύναμη ελατηρίου
η μέγιστη επιμήκυνση είναι Fελατ,max / k = 80 Ν / 80 Ν/m = 1 m
(Δ), (Ε) η μέγιστη ταχύτητα του σώματος είναι : 2 m/s από την σχέση :
υ(t) = 2 συν(4t + 3π/2)
η κατακόρυφη μετατόπιση του σώματος όταν έχει μέγιστη ταχύτητα είναι : x = 0,5 m θέση ισορροπίας για την ταλάντωση του σώματος
(Z) ο ρυθμός μεταβολής της κινητικής ενέργειας όταν κατέρχεται με υ = 2 m/s τότε α = 0
συνεπώς dK / dt = m v a = 0
(Α) ισορροπία σώματος : m g - T1 = 0 r = R/2
ισορροπία τροχαλίας : Στ(Ο) = 0 => T1 r - T2 R = 0 => T1 = 2 T2
ελατήριο : Τ2 = Fελατ = k Δl m g = 2 k Δl => Δl = mg / 2k αρχική επιμήκυνση του ελατηρίου όταν το σύστημα ισορροπεί
σώμα : ΣF = m g - T1 = m a (1)
τροχαλία : Στ(Ο) = Ι(Ο) αγων => T1 r - T2 R = ½ Μ R2 αγων =>
=> T1 R/2 - T2 R = ½ Μ R2 αγων =>
=> T1 - 2 T2 = Μ R αγων = Μ α (2)
ελατήριο : Τ2 = Fελατ = k ( x + Δl ) => 2 Τ2 = 2 k ( x + Δl ) (3)
(1) + (2) + (3) => m g = m a + Μ α + 2 k ( x + Δl ) =>
=> 0 = m a + Μ α + 2 k x =>
=> ( m + Μ ) α = - 2k x => α = - 2k /( m + Μ ) x συνεπώς το σώμα εκτελεί ΑΑΤ με συχνότητα ω2 = 2k /( m + Μ )
x(t) = Δl ημ(ωt + 3π/2) υ(t) = ωΔl συν(ωt + 3π/2)
α(t) = - ω2Δl ημ(ωt + 3π/2) ΣF(t) = m a(t) = - mω2 Δl ημ(ωt + 3π/2)
Fελατ(t)= k ( x + Δl ) = k Δl { 1 + ημ(ωt + 3π/2) }
Θέμα 17.
Στο σύστημα που φαίνεται στο σχήμα η μικρή τροχαλία Κ2 είναι μάζας
m2=1kg, ακτίνας r και το αβαρές σχοινί συνδέει τον κύλινδρο, Κ1, μάζας m1=8kg, ακτίνας r με το δίσκο, Κ, μάζας Μ=4kg και ακτίνας R. O κύλινδρος κυλίεται χωρίς να ολισθαίνει καθώς το τυλιγμένο σε αυτόν
νήμα ξετυλίγεται . Αν αφήσουμε το σύστημα ελεύθερο τη χρονική στιγμή t0=0, να υπολογιστούν:
Α. Οι επιταχύνσεις α1 και α των κέντρων μάζας Κ1 και Κ.
Β. Οι τάσεις όλων των νημάτων.
Γ. Η πτώση του κέντρου μάζας του δίσκου, Κ και η μετατόπιση του κέντρου μάζας του κυλίνδρου, Κ1 τη χρονική στιγμή t=2s.
Δ. Το ποσοστό της δυναμικής ενέργειας του δίσκου (Κ) που μετατράπηκε σε κινητικές ενέργειες του δίσκου, της τροχαλίας και του κυλίνδρου, μέχρι τη χρονική στιγμή t=2s.
Ε. Ο ρυθμός μεταβολής κινητικής ενέργειας του κυλίνδρου τη χρονική στιγμή t=2s.
(Α) r αγων,1 = α1 r αγων,2 = r αγων,1 + α1 = 2 α1
α = αγων R r aγων,2 = R αγων + α = 2 a άρα α = α1
Στ(Κ1) = Ι(Κ1) αγων,1 => ( F1 + T ) r = ½ m1 r2 aγων,1 => F1 + T = ½ m1 a1
ΣF = m1 a1 => F1 - T = m1 a1 οπότε F1 = 3/4 m1 a1
και T = F1 - m1 a1 = 3/4 m1 a1 - m1 a1 => T = - m1 a1 /4 η Τ είναι ομόρροπη της F1
Στ(Κ2) = Ι(Κ2) αγων,2 => ( F2 - F1 ) r = ½ m2 r2 aγων,2 => F2 - F1 = ½ m2 r aγων,2 = ½ m2 2a1 = m2 a1
ΣF = F2 - F1 = m2 a1 => F2 = ( 3/4 m1 + m2 ) a1
Στ(Κ) = Ι(Κ) αγων => (F3 - F2 ) R = ½ Μ R2 aγων => F3 - F2 = ½ Μ a = ½ M a1
Mg - F2 - F3 = M a = M a1 Mg - 2 F2 = M 3/2 a1
Mg - 2 ( 3/4 m1 + m2 ) a1 = M 3/2 a1 => Mg = ( 3/2 m1 + 2 m2 + 3/2 M ) a1
=> α1 = 40 / ( 12 + 2 + 6 ) = 40 / 20 => α1 = 2 m/s2 = α
(Β) οπότε F1 = 3/4 m1 a1 = 3/4 8 2 => F1 = 12 Ν και Τ = m1 a1 /4 = 8 2 /4 => Τ = 4 Ν
F2 = ( 3/4 m1 + m2 ) a1 = ( 3/4 8 + 1 ) 2 => F2 = 14 Ν
F3 - F2 = ½ Μ a = ½ M a1 => F3 - 14 = ½ 4 2 => F3 = 18 Ν
(Γ) y = ½ a t2 = ½ 2 22 = 4 m x1 = ½ a1 t2 = ½ 2 22 = 4 m
(Δ) vK = a t = 2 2 = 4 m/s vK1 = a1 t = 2 2 = 4 m/s ωK2 = αγων,2 . t = 2 α1 / r . t
M g y = ½ Μ υΚ2 + ½ ΙΚ ωΚ2 + ½ m1 υΚ12 + ½ ΙΚ1 ωΚ12 + ½ ΙΚ2 ωΚ22
M g y = ½ Μ υΚ2 + ½ ½ M R2 ωΚ2 + ½ m1 υΚ12 + ½ ½ m1 r2 ωΚ12 + ½ ½ m2 r2 (2 α1 / r . t )2
M g y = 3/4 Μ υΚ2 + 3/4 m1 υΚ12 + ½ ½ m2 r2 (2 α1 / r t )2
4 10 4 = 3/4 4 42 + 3/4 8 42 + ½ ½ 1 r2 4 α12 / r2 t2
160 = 48 + 96 + ½ ½ 1 4 22 22
160 = 48 + 96 + 16 η τριβή Τ δεν παράγει έργο ούτε καταναλώνει
ποσοστά κύλινδρος Κ1 : 96/160 60% τροχαλία Κ2 : 16/160 10% δίσκος Κ : 48/160 30%
(Ε) dK1/dt = m1 υΚ1 a1 + ΙΚ1 ωΚ1 aγων,1 = m1 υΚ1 a1 + ½ m1 r2 ωΚ1 aγων,1 =
= m1 υΚ1 a1 + ½ m1 υΚ1 a1 = 3/2 m1 υΚ1 a1 = 3/2 8 4 2 = 96 J/s
aλλιώς Κ1 = 3/4 m1 υΚ12 οπότε dK1/dt = 3/2 m1 υΚ1 a1 = 3/2 8 4 2 = 96 J/s
παρατηρούμε ότι :
το έργο της F1 : F1 x1 = 12N 4m = 48 J T x1 = 4N 4m = 16 J
F1 x1 + T x1 = 48 J + 16 J = 64 J = ½ 8 42 = ½ m1 υΚ12
F1 x1 - T x1 = 48 J - 16 J = 32 J = ½ ½ 8 42 = ½ ΙΚ1 ωΚ12

Θέμα 18.
Στο παρακάτω σχήμα φαίνεται η κάθετη τομή ενός καρουλιού, που αποτελείται από ένα κύλινδρο μάζας Μ1 =4 kg και ακτίνας R1 = 0,2 m και από δύο πανομοιότυπους δίσκους μάζας Μ2 =1 kg και ακτίνας R2 = 0,4m ο καθένας. Το καρούλι βρίσκεται σε τραχύ οριζόντιο δάπεδο. Γύρω από τον κύλινδρο έχουμε τυλίξει ένα αβαρές, λεπτό και μη εκτατό νήμα, στο ένα ελεύθερο άκρο του οποίου ασκούμε μία σταθερή δύναμη μέτρου F = 100 N. Το άλλο ελεύθερο άκρο του νήματος συνδέεται με σώμα Σ μάζας m =10 kg, το οποίο βρίσκεται πάνω σε λείο οριζόντιο επίπεδο δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k = 1000 Ν/m, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο σε κατακόρυφο τοίχο.  Αρχικά το σύστημα ισορροπεί και τη χρονική στιγμή t0 = 0 το νήμα που συνδέει το καρούλι με το σώμα Σ κόβεται, οπότε το σώμα Σ εκτελεί απλή αρμονική ταλάντωση πλάτους Α και σταθεράς επαναφοράς D=k, ενώ το καρούλι ξεκινά να κυλίεται χωρίς να ολισθαίνει .
Αρχικά το σύστημα ισορροπεί και τη χρονική στιγμή t0 = 0 το νήμα που συνδέει το καρούλι με το σώμα Σ κόβεται, οπότε το σώμα Σ εκτελεί απλή αρμονική ταλάντωση πλάτους Α και σταθεράς επαναφοράς D=k, ενώ το καρούλι ξεκινά να κυλίεται χωρίς να ολισθαίνει .
Δ1. Να γράψετε την εξίσωση της απομάκρυνσης σε συνάρτηση με το χρόνο για την απλή αρμονική ταλάντωση του σώματος Σ. Θεωρείστε θετική φορά προς τα δεξιά.
Δ2. Τη χρονική στιγμή t1 , όπου το σώμα Σ βρίσκεται στη μέγιστη απομάκρυνση από τη θέση ισορροπίας για πρώτη φορά, να υπολογίσετε το μέτρο της ταχύτητας του ανώτερου σημείου του δίσκου του καρουλιού.
Δ3. Να υπολογίσετε το ρυθμό μεταβολής της κινητικής ενέργειας του σώματος Σ και το ρυθμό μεταβολής της κινητικής ενέργειας του καρουλιού λόγω στροφικής κίνησης τη χρονική στιγμή t1.
Δ4. Να υπολογίσετε το έργο της δύναμης F από τη χρονική στιγμή t = 0 έως τη χρονική στιγμή t1.
Τη χρονική στιγμή t1 το νήμα που ήταν τυλιγμένο στον κύλινδρο εγκαταλείπει το καρούλι και ασκούμε ακαριαία στο κέντρο μάζας του καρουλιού μία οριζόντια δύναμη μέτρου F1 =30 Ν με αποτέλεσμα το καρούλι να ακινητοποιηθεί τη χρονική στιγμή t2.
Δ5. Να υπολογίσετε το συνολικό αριθμό περιστροφών από τη χρονική στιγμή t = 0 έως τη χρονική στιγμή t2, κατά την οποία το καρούλι ακινητοποιείται.
Δ1. ισορροπία σώματος Σ : Fελατ = Τ => k x0 = T (1) ισορροπία καρουλιού : Στ(Κ) = 0 => F R1 + T R1 = Ττριβ R2 => F 0,2 + T 0,2 = Ττριβ 0,4 => F + T = 2 Ττριβ (2)
ΣF = 0 => F - T + Ττριβ = 0 (3) (2) + (3) => 2 F = Ττριβ => Ττριβ = 2 100 Ν = 200 Ν οπότε από (3) => Τ = 100 + 200 = 300 Ν
και από (1) => x0 = T/ k = 300 / 1000 => x0 = 0,3 m επιμήκυνση ελατηρίου
ω2 = k / m = 1000 / 10 => ω = 10 rad/s x(t) = 0,3 ημ(10t + π/2) υ(t) = 3 συν(10t + π/2) a(t) = - 30 ημ(10t + π/2)
Δ2. t1 = Τ/2 = π/10 s
Ι(Κ) = ½ M1 R12 + 2 ½ M2 R22 = ½ 4 0,22 + 2 ½ 1 0,42 = 0,08 + 0,16 = 0,24 kg m2
ΣF = ( M1 + 2 M2 ) a => F + Ττριβ = ( M1 + 2 M2 ) R2 αγων => 100 + Ττριβ = (4 + 2) 0,4 αγων => 100 + Ττριβ = 2,4 αγων (4)
Στ(Κ) = Ι(Κ) αγων => F R1 - Ττριβ R2 = Ι(Κ) αγων => 100 0,2 - Ττριβ 0,4 = 0,24 αγων =>
=> 50 - Ττριβ = 0,6 αγων (5)
(4) + (5) => 150 = 3 αγων => αγων = 50 rad/s επιτάχυνση a = R2 αγων = 0,4 50 = 20 m/s2
v(Κ) = a t1 = 20 π/10 = 2π m/s ταχύτητα κέντρου μάζας καρουλιού
η ταχύτητα του του ανώτερου σημείου του δίσκου του καρουλιού : 2 2π m/s = 4π m/s
Δ3. ρυθμός μεταβολής κινητικής ενέργειας Σ :
dK/dt = m a v = 10 [- 30 ημ(10t + π/2)] 3 συν(10t + π/2) = - 900 ημ(10t + π/2) συν(10t + π/2)
t = π/10 s dK/dt = - 900 ημ(π + π/2) συν(π + π/2) = - 900 (-1) 0 = 0
ρυθμός μεταβολής κινητικής ενέργειας καρουλιού λόγω στροφικής κίνησης :
dK/dt = Ι(Κ) ω αγων = Ι(Κ) αγων t1 αγων = 0,24 50 π/10 50 = 60π J/s
Δ4. το κέντρο μάζας Κ του καρουλιού μετατοπίζεται κατά x1 = ½ α t12 = 0,5 20 (π/10)2 = 1 m
το νήμα ξετυλίγεται κατά l = θ1 R1 = ½ αγων t12 R1 = ½ 50 (π/10)2 0,2 = 2,5 rad 0,2 m = 0,5 m
το σημείο εφαρμογής της F μετατοπίζεται κατά : x1 + l = 1,5 m
έργο της F : WF = F ( x1 + l ) = 100 1,5 = 150 J
Δ5. o αριθμός περιστροφών : Ν1 = θ1 / 2π = 2,5 rad / 2π = 5/4π
η γωνιακή ταχύτητα : ω = αγων t1 = 50 π/10 = 5π rad/s
K = ½ Μ υ2 + ½ Ι(Κ) ω2 = ½ 6 (2π)2 + ½ 0,24 (5π)2 = 3 40 + 0,12 250 = 120 + 30 = 150 J
ΣF = ( M1 + 2 M2 ) a => - F1 + Ττριβ = ( M1 + 2 M2 ) R2 αγων => - F1 + Ττριβ = (4 + 2) 0,4 αγων => - F1 + Ττριβ = 2,4 αγων (6)
Στ(Κ) = Ι(Κ) αγων => - Tτριβ R2 = Ι(Κ) αγων => - Ττριβ 0,4 = 0,24 αγων => - Ττριβ = 0,6 αγων (7)
(6) + (7) => - F1 = 3 αγων => αγων = - 30/3 = - 10 rad/s2
ω2 = ω1 + αγων Δt => 0 = 5π + (-10) Δt => Δt = π/2 s
θ2 = ω Δt + ½ αγων Δt2 = 5π π/2 + ½ (-10) (π/2)2 = 25 - 12,5 = 12,5 rad π2 = 10
N2 = θ2 / 2π = 12,5 / 2π = 25/4π περιστροφές
συνολικός αριθμός περιστροφών = 5/4π + 25/4π = 30/4π = 15/2π

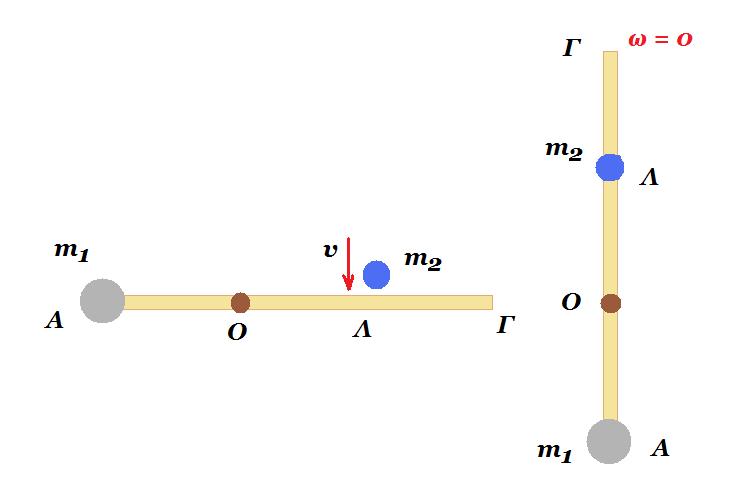 Λεπτή ομογενής ράβδος ΑΓ έχει μάζα Μ = 2 kg μήκος l = 3 m και μπορεί να περιστέφεται στο κατακόρυφο επίπεδο χωρίς τριβές γύρω από σταθερό οριζόντιο σταθερό άξονα που διέρχεται από σημείο της Ο. Στο άκρο Α της ράβδου είναι στερεωμένη σημειακή μάζα m1 = 1 kg.
Λεπτή ομογενής ράβδος ΑΓ έχει μάζα Μ = 2 kg μήκος l = 3 m και μπορεί να περιστέφεται στο κατακόρυφο επίπεδο χωρίς τριβές γύρω από σταθερό οριζόντιο σταθερό άξονα που διέρχεται από σημείο της Ο. Στο άκρο Α της ράβδου είναι στερεωμένη σημειακή μάζα m1 = 1 kg. Θέμα 20.