Σε λείο οριζόντιο επίπεδο βρίσκονται ακίνητα δύο σώματα Σ1 και Σ2 με μάζες m1 = 1kg και m2 = 3kg αντίστοιχα. Tα σώματα είναι σε επαφή με ιδανικό ελατήριο σταθεράς Κ = 1200N/m, το οποίο βρίσκεται στο φυσικό του μήκος. Τη χρονική στιγμή t0 = 0 εκτοξεύουμε το σώμα Σ1 προς τα δεξιά με ταχύτητα μέτρου υ0 = 10m/s. Κάποια στιγμή t1 το μέτρο της ταχύτητας του σώματος Σ2 είναι ίσο με υ2 = 1m/s . Ο ρυθμός dUελ / dt μεταβολής της δυναμικής ενέργειας του ελατηρίου τη στιγμή t1 είναι ίσος με:
α. -1680 J/s β. 240 J/s γ. 1440 J/s
m1 v0 = m1 v1 + m2 v2 => 1 10 = 1 v1 + 3 1 => v1 = 7 m/s
½ m1 v02 = ½ m1 v12 + ½ m2 v22 + ½ k x2 => 1 100 = 1 49 + 3 1 + 1200 x2 => 48 / 1200 = x2 => x = 0,2 m
dUελ / dt = k x Fελ = k x = 1200 0,2 = 240 N
ΣF1 = m1 a1 => - 240 N = 1 kg a1 => a1 = - 240 m/s2
ΣF2 = m2 a2 => + 240 N = 3 kg a2 => a2 = + 80 m/s2
K1 + K2 + Uελατ = σταθερό => ΔK1 + ΔK2 + ΔUελατ = 0 => ΔK1 / Δt + ΔK2 / Δt + ΔUελατ / Δt = 0 =>
=> m1 v1 a1 + m2 v2 a2 + ΔUελατ / Δt = 0 => 1 7 (-240) + 3 1 80 + ΔUελατ / Δt = 0 =>
=> - 1680 + 240 + ΔUελατ / Δt = 0 => ΔUελατ / Δt = 1440 J/s
v1 = v0 - g ημφ t v2 = g ημφ t v1 + v2 = v0 => v1 + 3/2 v1 = v0 => v1 = 2/5 v0
m1 v1 - 2/3 m1 v2 = 0 => v1 = 2/3 v2 => 3/2 v1 = v2
Kαρχ = ½ m1 v12 + ½ 2/3 m1 v22 = ½ m1 v12 + 1/3 m1 9/4 v12 = ½ m1 v12 + 3/4 m1 v12 = 5/4 m1 v12 = 5/4 m1 4/25 v02 = 1/5 m1 v02
............................................................................................
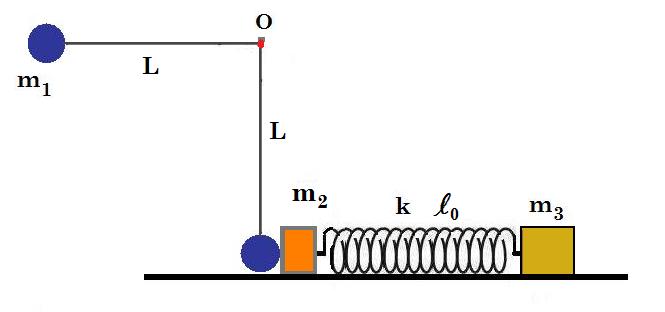
Δύο σώματα, Σ2,Σ3, με μάζες m2= 0,4kg και m3= 0,6kg συνδέονται με ελατήριο σταθεράς k=24Ν/m και τοποθετούνται σε λείο οριζόντιο επίπεδο με το ελατήριο αρχικά στο φυσικό του μήκος. Σφαίρα Σ1, μάζας m1=0,2kg είναι δεμένη στο άκρο αβαρούς νήματος μήκους L= 0,45m που κρέμεται από ακλόνητο σημείο Ο. Εκτρέπουμε το νήμα από την κατακόρυφη θέση κατά 90° και αφήνουμε τη σφαίρα Σ1 ελεύθερη. Τη στιγμή που το νήμα γίνεται κατακόρυφο η σφαίρα συγκρούεται κεντρικά και ελαστικά με το σώμα Σ2. Αμέσως μετά την κρούση το ελατήριο συμπιέζεται και βάζει σε κίνηση και το σώμα Σ3. Να βρεθούν:
α. Οι ταχύτητες των σωμάτων Σ1 και Σ2 μετά την κρούση.
β. Οι ταχύτητες των σωμάτων Σ2 και Σ3 τη στιγμή που το ελατήριο θα βρίσκεται στη μέγιστη συσπείρωσή του.
γ. Η μέγιστη συσπείρωση του ελατηρίου.
δ. Οι ταχύτητες των σωμάτων Σ2 και Σ3 τη στιγμή που το ελατήριο απόκτά και πάλι το φυσικό του μήκος. Δίνεται g=10m/s2.
ΑΠ: α. −1m/s, 2m/s, β. 0,8m/s, γ. 0,2m, δ. -0,4m/s, 1,6m/s
διατήρηση ενέργειας Σ1 : m1 g L = ½ m1 v12 => v12 = 2gL = 2 10 0,45 = 9 => v1 = 3 m/s
κεντρική - ελαστική κρούση Σ1 - Σ2 : v1' = v1 (m1 - m2) / (m1 + m2) = 3 (0,2 - 0,4) / (0,2 + 0,4) = - 1 m/s
v2' = 2 m1 v1 / m1 + m2) = 2 0,2 3 / (0,2 + 0,4) = 2 m/s
μετά την κρούση θα κινηθούν τα σώματα Σ2 και Σ3 ενώ το ελατήριο συσπειρώνεται
η μέγιστη συσπείρωση θα συμβεί όταν τα σώματα Σ2 και Σ3 αποκτήσουν ίσες ταχύτητες
διατήρηση ορμής : m2 v2' = m2 u + m3 u => 0,4 2 m/s = 0,4 u + 0,6 u => 4 m/s = 5 u => u = 0,8 m/s
διατήρηση ενέργειας : ½ m2 v2' 2 = ½ m2 u2 + ½ m3 u2 + ½ k x2 =>
0,4 22 = 0,4 0,82 + 0,6 0,82 + 24 x2 => 1,6 = 0,64 + 24 x2 => 0,96 / 24 = x2 => x2 = 0,04 => x = 0,2 m μέγιστη συσπείρωση ελατηρίου
διατήρηση ορμής : m2 v2' = m2 u2 + m3 u3 => 0,4 2 m/s = 0,4 u2 + 0,6 u3 => 4 m/s = 2 u2 + 3 u3
διατήρηση ενέργειας : ½ m2 v2' 2 = ½ m2 u2 + ½ m3 u2 + ½ k x2 => 0,4 22 = 0,4 u22 + 0,6 u32 =>
1,6 = 0,4 u22 + 0,6 u32 => 8 = 2 u22 + 3 u32 => 8 = 2 ( 2 - 1,5 u3 )2 + 3 u32 =>
=> 8 = 2 ( 4 - 6 u3 + 2,25 u32 ) + 3 u32 => 8 = 8 - 12 u3 + 4,5 u32 + 3 u32 =>
=> 7,5 u32 - 12 u3 = 0 => u3 = 0 αρχική ταχύτητα u3 = 12/7,5 = 24/15 = 8/5 => u3 = 1,6 m/s δεκτή λύση
4 m/s = 2 u2 + 3 u3 => 4 m/s = 2 u2 + 3 1,6 => u2 = (4 - 4,8) / 2 => u2 = - 0,4 m/s
.....................................................................................................
Δύο σώματα με μάζες m1=10kg και m2 κινούνται σε λείο οριζόντιο επίπεδο και κατά μήκος του ίδιου άξονα x'Οx. Η ταχύτητα της m1 είναι υ1=6m/s, ενώ της m2 είναι υ2 αλλά με αντίθετη κατεύθυνση. Τα δύο σώματα συγκρούονται μετωπικά ελαστικά και μετά την κρούση ανταλλάσσουν τις ορμές τους. Μετά την κρούση το μέτρο της ταχύτητας του σώματος m2 γίνεται υ2'=4m/s. Να υπολογιστούν:
α. Η μάζα m2. β. Η ταχύτητα υ2. γ. Η μεταβολή της ορμής του σώματος m2.
v1' = v1 (m1 - m2) / (m1 + m2) + 2 m2 v2 / (m1 + m2) => v1' = 6 (10 - m2) / (10 + m2) + 2 m2 v2 / (10 + m2)
v2' = v2 (m2 - m1) / (m1 + m2) + 2 m1 v1 / (m1 + m2) => 4 = v2 (m2 - 10) / 10 + m2) + 2 10 6 / (10 + m2)
διατήρηση ορμής :
m1 v1 - m2 v2 = m1 v1' + m2 v2' => 10 6 + m2 v2 = 10 v1' + m2 4 => 10 6 + 15 v2 = 10 v1' + 15 4 =>
ανταλλάσσουν τις ορμές : m2 v2' = m1 v1 => m2 4 = 10 6 => m2 = 15 kg
m1 v1' = - m2 v2 => 10 v1' = - 15 v2 => δεν τελείωσε
............................................................................................................................
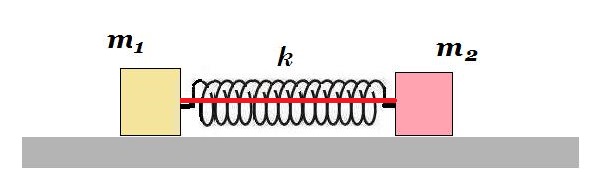m2 = 3m1
διατήρηση ορμής :
0 = m1 v1 + m2 v2 => 0 = m1 v1 + 3m1 v2 => v1 = -3v2
διατήρηση ενέργειας :
½ m1 v12 + ½ m2 v22 = ½ k x2 = U => m1 (-3v2)2 + 3m1 v22 = 2U => 12m1 v22 = 2U => v22 = U/6m1
v1 = -3v2 = - ( 3U/2m1 )½
m1 = 3m2
διατήρηση ορμής :
0 = m1 v1 + m2 v2 => 0 = 3m2 v1 + m2 v2 => v2 = -3v1
διατήρηση ενέργειας :
½ m1 v12 + ½ m2 v22 = ½ k x2 = U => m1 v12 + m1/3 (-3v1)2 = 2U => 4m1 v12 = 2U => v12 = U/2m1
....................................................................................................................................................................
Βλήμα μάζας m κινούμενο οριζόντια με ταχύτητα υ1=200m/s, διαπερνάει ξύλινο πρίσμα μάζας Μ=2m, μήκους d=0,5m το οποίο αρχικά ηρεμούσε πάνω σε λείο οριζόντιο επίπεδο. Το βλήμα βγαίνει από το πρίσμα μετά από χρονικό διάστημα Δt με οριζόντια ταχύτητα μέτρου υ2=100m/s. Αν η δύναμη αντίστασης του ξύλου πάνω στο βλήμα θεωρηθεί σταθερή, να υπολογιστούν:
α. Η ταχύτητα,V, του πρίσματος τη χρονική στιγμή που το βλήμα βγαίνει απ' αυτό.
β. Η μετατόπιση, Δx, του πρίσματος στο χρονικό διάστημα Δt που το βλήμα το διαπερνούσε.
γ. Το χρονικό διάστημα Δt.
δ. Το ποσοστό, (%), της κινητικής ενέργειας του βλήματος που έγινε θερμότητα λόγω τριβής του
βλήματος με το υλικό του πρίσματος.
η συνισταμένη των δυνάμεων που ενεργούν στα σώματα είναι μηδέν οπότε η ορμή διατηρείται
m v1 = m v2 + M V => m 200 = m 100 + 2m V => V = 50 m/s
F = Δp / Δt = ( M V - 0 ) / Δt = M 50 / Δt = M a1 => a1 = 50 / Δt επιτάχυνση
F = Δp/Δt = (m v2 - m v1) / Δt = m (100 - 200) / Δt = - 100 m / Δt = m a2 => a2 = - 100 / Δt επιβράδυνση
Δx1 = ½ α1 Δt2 = ½ 50 / Δt Δt2 = 25 Δt
Δx2 = υ1 Δt + ½ α2 Δt2 = 200 Δt - ½ 100 Δt = 150 Δt
Δx2 - Δx1 = d => 150 Δt - 25 Δt = 0,5m => Δt = 0,5/125 s = 1/250 s
a1 = 50 / Δt = 50 / 1/250 = 12500 m/s2 a2 = - 100 / Δt = - 100 / 1/250 = - 25000 m/s2
Δx1 = 25 Δt = 25 1/250 = 0,1 m Δx2 = 150 Δt = 150 1/250 = 15/25 = 0,6 m
Kτελ = ½ m v22 + ½ M V2 = ½ m 1002 + ½ 2m 502 = 5000 m + 2500 m = 7500 m
Kαρχ = ½ m v12 = ½ m 2002 = 20000 m
ΔΚ = Κτελ - Καρχ = - 12500 m Qθερμ = - ΔΚ = 12500 m Qθερμ / K1 = 0,625 ή 62,5%
.....................................................................................................................................................................
m1 = m2 = m3 = m , λείο οριζόντιο επίπεδο , αρχικά : m1 , m2 ακίνητα , το ελατήριο έχει το φυσικό του μήκος , το m3 κινείται με ταχύτητα υ και συγκρούεται κεντρικά - ελαστικά με το m1
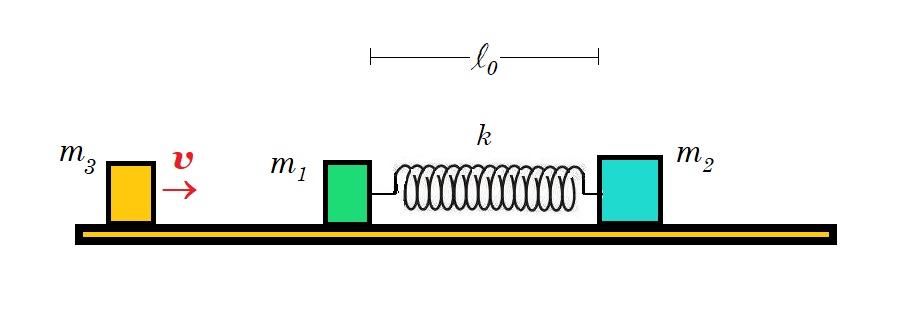
κατά την κρούση Σ1 , Σ3 ανταλλάσουν ταχύτητες διότι έχουν ίσες μάζες , οπότε το Σ3 θα μείνει ακίνητο και το Σ1 θα κινηθεί προς τα δεξιά με ταχύτητα υ
τα Σ1 , Σ2 συνδέονται με το ελατήριο
διατήρηση ορμής : m1 v = m1 u1 + m2 u2 => v = u1 + u2 => v2 = u12 + u22 + 2 u1 u2 (1)
διατήρηση ενέργειας : ½ m1 v2 = ½ m1 u12 + ½ m2 u22 + ½ k x2 =>
=> v2 = u12 + u22 + k x2 / m =>(1) u12 + u22 + 2 u1 u2 = u12 + u22 + k x2 / m =>
=> 2 u1 u2 = k x2 / m > 0 (2) συμπεραίνουμε ότι οι ταχύτητες των σωμάτων είναι ομόρροπες
(2) => u2 = k.x2/ 2.m.u1
η σχέση : v = u1 + u2 => v = u1 + k.x2/ 2.m.u1 => v.2.m.u1 = 2.m.u12 + k.x2 =>
=> 2.m.u12 - 2.m.v.u1 + k.x2 = 0
Δ = 4.m2.v2 - 8.m.k.x2 ³ 0 => x2 £ m.v2/2.k
η μέγιστη συσπείρωση του ελατηρίου είναι : xμέγιστη = (m/2.k)½.v όταν Δ = 0
οι ρίζες του τριωνύμου : ρ1,2 = - ( - 2.m.v )/ 4.m = υ/2 = u1
οπότε από τη σχέση v = u1 + u2 => u2 = υ/2 = u1
οι ταχύτητες u1 , u2 , υ είναι ομόρροπες
........................................................................................................................
Επάνω σε λείο οριζόντιο επίπεδο κινείται σώμα Σ1 μάζας m1 με σταθερή ταχύτητα υ1. Το σώμα Σ1 συναντά το άκρο ελατηρίου που έχει το φυσικό του μήκος, ενώ στο άλλο του άκρο είναι δεμένο σώμα Σ2 μάζας m2 που είναι ακίνητο επάνω στο λείο οριζόντιο επίπεδο. Η διεύθυνση της ταχύτητας υ1 συμπίπτει με τον άξονα του ελατηρίου. Δείξτε ότι το ελατήριο συσπειρώνεται κατά το μέγιστον όταν τα σώματα αποκτήσουν ίσες ταχύτητες.
διατήρηση ορμής :
m1 v1 = m1 v1' + m2 v2' => v1' = v1 - v2' m2/m1 (1)
διατήρηση ενέργειας :
½ m1 v12 = ½ k x2 + ½ m1 v1'2 + ½ m2 v2'2
m1 v12 - m1 v1'2 = k x2 + m2 v2'2
m1 ( v1 - v1' ) ( v1 + v1' ) = k x2 + m2 v2'2
m2 v2' ( v1 + v1 - v2' m2/m1 ) = k x2 + m2 v2'2
m2 v2' ( 2 v1 - v2' m2/m1 ) = k x2 + m2 v2'2
2 m2 v2' v1 - v2'2 m22 /m1 = k x2 + m2 v2'2
0 = k x2 + m2 v2'2 - 2 m2 v2' v1 + v2'2 m22 /m1
0 = ( m2 + m22 /m1 ) v2'2 - 2 m2 v1 v2' + k x2 (2) τριώνυμο ως προς v2'
Δ = 4 m22 v12 - 4 ( m2 + m22 /m1 ) k x2 ³ 0 => m22 v12 ³ ( m2 + m22 /m1 ) k x2 =>
=> m1 m2 v12 / ( m1 + m2 ) k ³ x2
η μέγιστη συσπείρωση του ελατηρίου είναι : xμέγιστη = v1 { m1 m2 / (m1 + m2).k }½ όταν Δ = 0 τότε οι ρίζες του τριωνύμου : ρ1,2 = - β / 2α = - ( - 2 m2 v1 ) / 2( m2 + m22 /m1 ) =
= v1 / ( 1 + m2 /m1 ) => v2' = v1 / ( 1 + m2 /m1 ) => v2' = v1 m1 / ( m1 + m2 )
από τη σχέση (1) έχουμε : v1' = v1 - v2' m2/m1 => v1' = v1 - ( m2/m1 ) v1 m1 / ( m1 + m2 ) =>
=> v1' = v1 - m2 v1 / ( m1 + m2 ) = ( m1 v1 + m2 v1 - m2 v1 ) / ( m1 + m2 ) =>
=> v1' = m1 v1 / ( m1 + m2 )
άλλος τρόπος
f (v2') = ( m2 + m22 /m1 ) v2'2 - 2 m2 v2' v1 + k x2
f '(v2') = 2 ( m2 + m22 /m1 ) v2' - 2 m2 v1
ακρότατο : f '(v2') = 0 => 2 ( m2 + m22 /m1 ) v2' - 2 m2 v1 = 0 =>
=> ( m2 + m22 /m1 ) v2' = m2 v1 =>
=> ( 1 + m2 /m1 ) v2' = v1 =>
=> v2' = v1 m1 / ( m1 + m2 )
v1' = v1 - m2/m1 v2' = v1 - m2/m1 v1 m1 / ( m1 + m2 ) =
= v1 - m2 v1 / ( m1 + m2 ) = [ v1 ( m1 + m2 ) - m2 v1 ] / ( m1 + m2 ) =
= [ v1 m1 + v1 m2 - m2 v1 ] / ( m1 + m2 ) = v1 m1 / ( m1 + m2 ) = v1' = v2'
(2) => ( m2 + m22 /m1 ) v2'2 - 2 m2 v2' v1 + k x2 = 0 =>
=> m2 ( m1 + m2 )/m1 v12 m12 / ( m1 + m2 )2 - 2 m2 v1 v1 m1 / ( m1 + m2 ) + k x2 = 0 =>
=> m1 m2 v12 / ( m1 + m2 ) - 2 m1 m2 v12 / ( m1 + m2 ) + k x2 = 0 =>
=> - m1 m2 v12 / ( m1 + m2 ) + k x2 = 0 =>
=> x2 = m1 m2 v12 / k(m1 + m2) => x = v1 [ m1 m2 / k(m1 + m2) ]½ μέγιστη συσπείρωση του ελατηρίου
....................................................................................................................................................................................
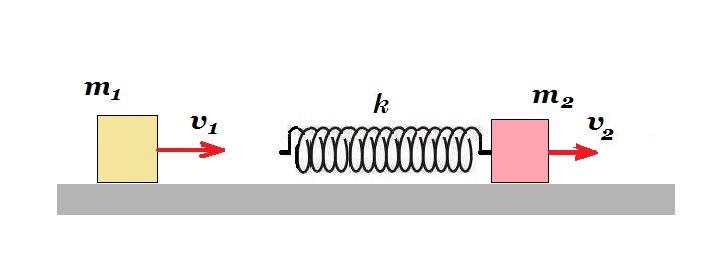
Σώμα Σ1 μάζας m1=3kg ολισθαίνει χωρίς τριβές πάνω σε οριζόντιο επίπεδο με ταχύτητα υ1=6m/s. Μπροστά απ' αυτό, άλλο σώμα Σ2 μάζας m2 =9kg ολισθαίνει στην ίδια κατεύθυνση και με ταχύτητα υ2=2m/s. Το σώμα Σ2 φέρει πίσω του στερεωμένο οριζόντιο ελατήριο σταθεράς k=100Ν/m, αμελητέας μάζας. Κατά τη σύγκρουση που ακολουθεί το ελατήριο παραμορφώνεται τα σώματα πλησιάζουν και στην συνέχεια απομακρύνονται, μέχρι να αποκτήσει και πάλι το ελατήριο το φυσικό του μήκος. Να υπολογιστούν:
α. Η ταχύτητα των σωμάτων τη στιγμή που το ελατήριο έχει μέγιστη συσπείρωση.
β. Η μέγιστη συσπείρωση του ελατηρίου.
γ. Οι ταχύτητες των σωμάτων όταν το ελατήριο επανέρχεται στο φυσικό του μήκος.
δ. Οι ρυθμοί μεταβολής της ταχύτητας των σωμάτων στη θέση της μέγιστης συσπείρωσης.
(a) (β) διατήρηση ορμής :
m1 v1 + m2 v2 = m1 v1' + m2 v2' => 3 6 + 9 2 = 3 v1' + 9 v2' => v1' = 12 - 3 v2' (1)
διατήρηση ενέργειας :
½ m1 v12 + ½ m2 v22 = ½ k x2 + ½ m1 v1'2 + ½ m2 v2'2
3 62 + 9 22 = 100 x2 + 3 v1'2 + 9 v2'2
62 + 3 22 = 100/3 x2 + v1'2 + 3 v2'2
48 = 100/3 x2 + (12 - 3 v2')2 + 3 v2'2
48 = 100/3 x2 + 144 - 72 v2' + 9 v2'2 + 3 v2'2
12 v2'2 - 72 v2' + 96 + 100/3 x2 = 0
Δ = 722 - 4 12 ( 96 + 100/3 x2 ) = 722 - 4 12 ( 96 + 100/3 x2 ) = 5184 - 4608 + 1600 x2 = 576 - 1600 x2
Δ = 0 => x2 = 576 / 1600 = 0,36 => x = 0,6 m μέγιστη συσπείρωση ελατηρίου
v2' = - β / 2α = - (-72) / 24 = 3 m/s (1) => v1' = 12 - 3 3 = 3 m/s
(γ) διατήρηση ορμής :
m1 v1 + m2 v2 = m1 v1' + m2 v2' => 3 6 + 9 2 = 3 v1' + 9 v2' => v1' = 12 - 3 v2' (1)
διατήρηση ενέργειας :
½ m1 v12 + ½ m2 v22 = ½ m1 v1'2 + ½ m2 v2'2
3 62 + 9 22 = 3 v1'2 + 9 v2'2
62 + 3 22 = v1'2 + 3 v2'2
48 = (12 - 3 v2')2 + 3 v2'2
48 = 144 - 72 v2' + 9 v2'2 + 3 v2'2
12 v2'2 - 72 v2' + 96 = 0
Δ = 722 - 4 12 96 = 5184 - 4608 = 576 Δ½ = 576½ = 24
v2' = (- β ± Δ½) / 2α = (72 ± 24) / 24 = 2 m/s αρχική τιμή ή 4 m/s δεκτή
(1) => v1' = 12 - 3 4 = 0 m/s
(δ) F = Δp / Δt => - k x = m1 ( v1' - v1 ) / Δt => - k x = m1 Δv1 / Δt => Δv1 / Δt = - k x / m1
Δv1 / Δt = - 100 0,6 / 3 = - 20 m/s2
F = Δp / Δt => k x = m2 ( v2' - v2 ) / Δt => k x = m2 Δv2 / Δt => Δv1 / Δt = k x / m2
Δv2 / Δt = 100 0,6 / 9 = 20/3 m/s2
..............................................................................................................................................................................
1. Σώμα μάζας m που κινείται με ταχύτητα υ = 12 m/s συγκρούεται μετωπικά ελαστικά με ακίνητο σώμα τριπλάσιας μάζας.Υπολογίστε τις ταχύτητες των σωμάτων μετά την κρούση.
υ1' = (m - 3m)/(m + 3m) . v = - 0,5 . 12 m/s = - 6 m/s
υ2' = 2.m.v / (m + 3m) = + 0,5 . 12 m/s = + 6 m/s
2. Σφαίρα (1) μάζας m1 = 1 kg προσπίπτει με ταχύτητα υ1 σε ακίνητη σφαίρα (2) και συγκρούεται κεντρικα ελαστικά με αυτή. Μετά την κρούση η (1) κινείται με ταχύτητα μέτρου υ1' = υ1/3. Ποια πρέπει να είναι η μάζα m2 της σφαίρας (2) ώστε : α) η υ1' να είναι ομόρροπη της υ1 β) η υ1' να είναι αντίρροπη της υ1 ;
υ1' = (m1 - m2 )/(m1 + m2 ) . v1 => υ1/3 = (m1 - m2 )/(m1 + m2 ) . v1 => 3 . (m1 - m2 ) = m1 + m2 => 2 . m1 = 4 . m2 => m2 = 0,5 kg
υ1' = (m1 - m2 )/(m1 + m2 ) . v1 => - υ1/3 = (m1 - m2 )/(m1 + m2 ) . v1 => - 3 . (m1 - m2 ) = m1 + m2 => 4 . m1 = 2 . m2 => m2 = 2 kg
3. Σφαίρα μάζας m1 συγκρούεται ελαστικά με σφαίρα μάζας m2 που αρχικά ηρεμεί. Η κρούση δεν είναι κεντρική. Δείξτε ότι : αν m1 = m2 τότε οι σφαίρες θα κινηθούν σε διευθύνσεις κάθετες μεταξύ τους και το αντίστροφο.
m1 = m2 : Καρχ = Κτελ => p12 / 2m1 = (p1')2 / 2m1 + (p2')2 / 2m2 => p12 = (p1')2 + (p2')2 (1)
pαρχ = pτελ => p12 = (p1')2 + (p2')2 + 2 . p1'.p2'.συνθ =>(1) (p1')2 + (p2')2 = (p1')2 + (p2')2 + 2.p1'.p2'.συνθ => συνθ = 0 => θ = 90°
άλλος τρόπος :
άξονας y : m1 v1' ημθ1 = m2 v2' ημθ2 => v1' ημθ1 = v2' ημθ2 (1)
άξονας x : m1 v1 = m1 v1' συνθ1 + m2 v2' συνθ2 => v1 = v1' συνθ1 + v2' συνθ2 =>
=> v12 = (v1')2 συν2θ1 + (v2')2 συν2θ2 + 2 v1' συνθ1 v2' συνθ2 (2)
Καρχ = Κτελ => ½ m1 v12 = ½ m1 (v1')2 + ½ m2 (v2')2 => v12 = (v1')2 + (v2')2 =>
=> v12 = (v1')2 συν2θ1 + (v1')2 ημ2θ1 + (v2')2 συν2θ2 + (v2')2 ημ2θ2 (3)
(2) - (3) => v12 - v12 = (v1')2 συν2θ1 + (v2')2 συν2θ2 + 2 v1' συνθ1 v2' συνθ2 -
- { (v1')2 συν2θ1 + (v1')2 ημ2θ1 + (v2')2 συν2θ2 + (v2')2 ημ2θ2 } =>
=> 0 = + 2 v1' συνθ1 v2' συνθ2 - (v1')2 ημ2θ1 - (v2')2 ημ2θ2 (1)=>
(1)=> 0 = + 2 v1' συνθ1 v2' συνθ2 - (v1')2 ημ2θ1 - (v1')2 ημ2θ1 =>
=> 0 = + 2 v1' συνθ1 v2' συνθ2 - 2 (v1')2 ημ2θ1 =>
=> 2 v1' συνθ1 v2' συνθ2 = 2 (v1')2 ημ2θ1 => συνθ1 v2' συνθ2 = v1' ημ2θ1 =>
=> συνθ1 v2' συνθ2 = v1' ημθ1 ημθ1 (1)=> συνθ1 v2' συνθ2 = v2' ημθ2 ημθ1 =>
=> συνθ1 συνθ2 = ημθ2 ημθ1 => συνθ1 συνθ2 - ημθ2 ημθ1 = 0 =>
=> συν( θ1 + θ2 ) = 0 = συν90° => θ1 + θ2 = 90°
θ = 90° : pαρχ = pτελ => p12 = (p1')2 + (p2')2 + 2 . p1'.p2'.συνθ => p12 = (p1')2 + (p2')2 =>
Καρχ = Κτελ => p12 / 2m1 = (p1')2 / 2m1 + (p2')2 / 2m2 =>
=> { (p1')2 + (p2')2 } / 2m1 = (p1')2 / 2m1 + (p2')2 / 2m2 => (p2')2 / 2m1 = (p2')2 / 2m2 => m1 = m2
4. Σε λείο οριζόντιο επίπεδο σφαίρα μάζας m1 = m κινούμενη με ταχύτητα υ0 συγκρούεται ελαστικά με σφαίρα μάζας m2 = m που αρχικά ηρεμεί. Η κρούση δεν είναι κεντρική. Λόγω της κρούσης η σφαίρα 1 χάνει το 75% της κινητικής της ενέργειας. Θεωρούμε τη στιγμή t = 0 αμέσως μετά την κρούση, τότε η απόσταση των σφαιρών συναρτήσει του χρόνου είναι :
α) d = ½ . v0 . t β) d = v0 . t γ) d = 3½/2 . v0 . t
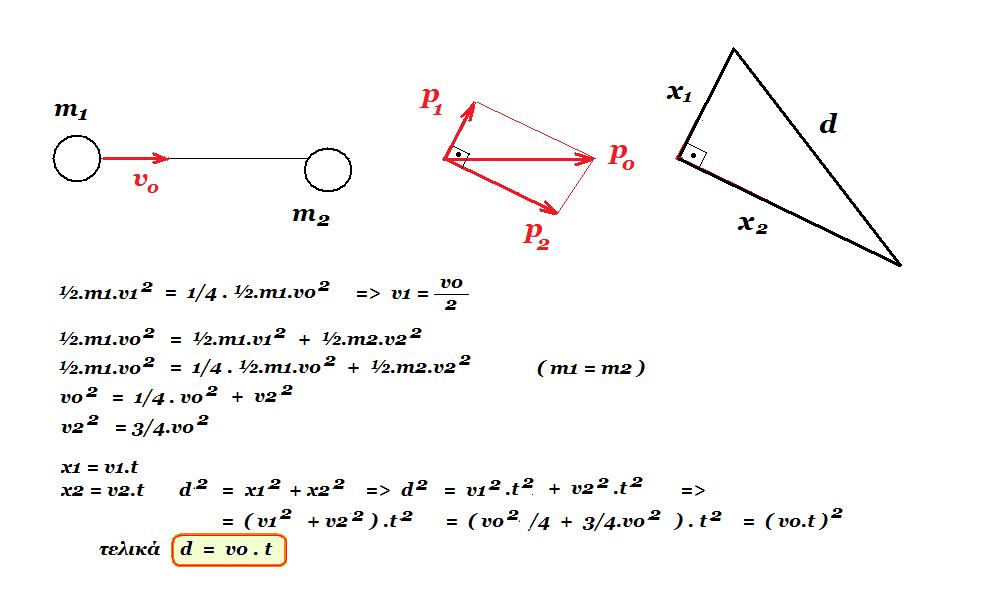
5. Δύο σώματα με μάζες m1 = m και m2 = 1,5. m κινούνται χωρίς τριβές στο ίδιο οριζόντιο επίπεδο και σε κάθετες μεταξύ τους διευθύνσεις με ταχύτητες υ1 =2.υ και υ2 = υ και συγκρούονται πλαστικά. Πόσο είναι το ποσοστό της αρχικής κινητικής ενέργειας του συστήματος που μετατρέπεται σε θερμότητα;
(m1 . 2.υ)2 + ( m2 . υ)2 = ( m1 + m2 )2 . υ'2 =>
(m . 2.υ)2 + ( 1,5.m . υ)2 = ( m + 1,5.m )2 . υ'2 =>
4 . (m .υ)2 + 2,25 . (m . υ)2 = 6,25 . m2 . υ'2 =>
6,25 . υ2 = 6,25 . υ'2 => υ' = υ
Καρχ = ½ . m1 . (2.υ)2 + ½ . m2 . υ2 = ½ . m . (2.υ)2 + ½ . 1,5 . m . υ2 = 11/4 . m .υ2
Κτελ = ½ . 2,5.m . (υ)2 = 5/4 . m . υ2
ΔΚ = Καρχ - Κτελ = 11/4 . m .υ2 - 5/4 . m .υ2 = 6/4 . m .υ2
ΔΚ / Καρχ = 6/4 . m .υ2 / 11/4 . m .υ2 = 6/11 ή 600/11 %
6. Σώμα Σ2 μάζας m2 = 4 kg βρίσκεται πάνω σε λείο οριζόντιο επίπεδο. Πάνω στο Σ2 βρίσκεται σώμα Σ1 μάζας m1 = 950 g Το επίπεδο επαφής των σωμάτων είναι οριζόντιο και ο συντελεστής τριβής ολισθήσεως μεταξύτων είναι μ = 0,5. Στο Σ1 σφηνώνεται σφαίρα μάζας mσ = 50 g που κινείται οριζόντια με ταχύτητα υσ = 100 m/s. Η χρονική διάρκεια της κρούσης θεωρείται αμελητέα.
α) Μετά από πόσο χρόνο από τη στιγμή της κρούσης τα σώματα Σ1 και Σ2 αποκτούν την ίδια ταχύτητα;
β) Πόσο μετακινήθηκε το συσσωμάτωμα σφαίρα - Σ1 μέχρι τη στιγμή αυτή;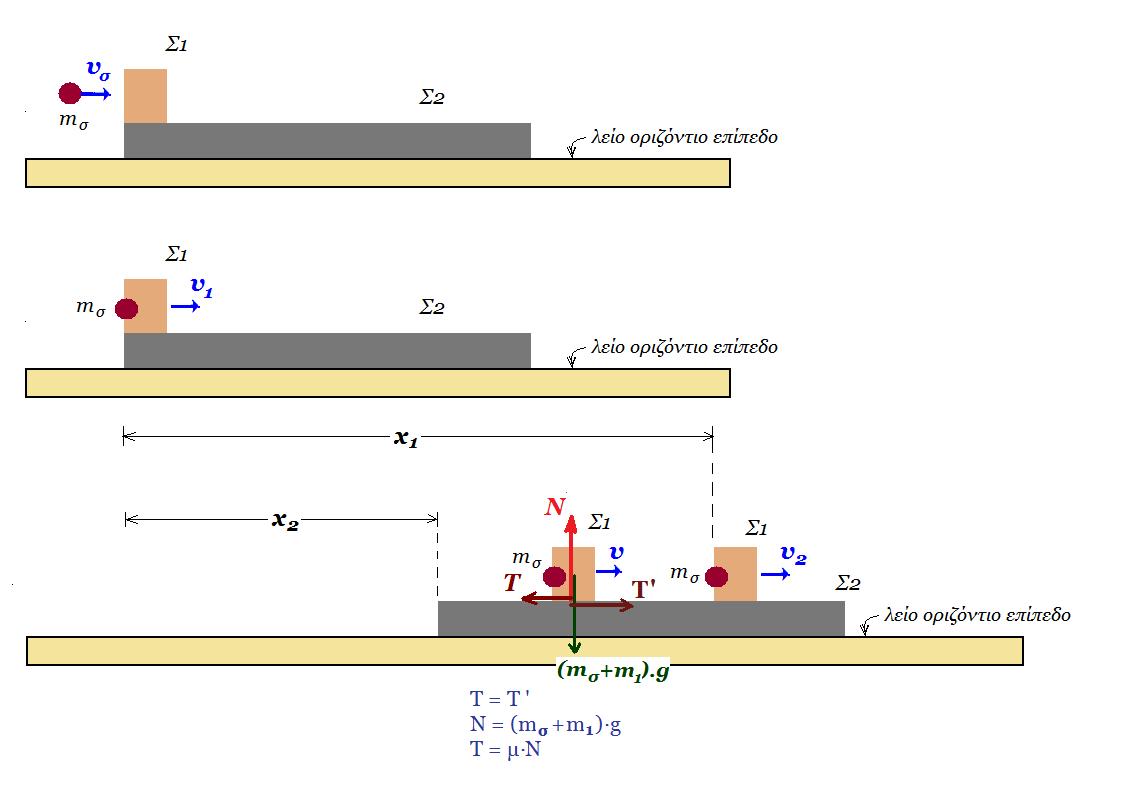 
mσ . υσ = ( mσ + m1 ). υ1 => 50. 100 = (50 + 950). υ1 => υ1 = 5 m/s
( mσ + m1 ). υ1 = ( mσ + m1 + m2 ). υ2 => 1 . 5 = (1 + 4) . v2 => υ2 = 1 m/s
T = T' T = μ . Ν = μ . ( mσ + m1 ).g = 0,5 . 1 . 10 => T = T' = 5 N
ΣF = ( mσ + m1 ).α1 => Τ = ( mσ + m1 ).α1 => μ . ( mσ + m1 ).g = ( mσ + m1 ).α1 => a1 = μ . g = 0,5 . 10 => a1 = 5 m/s2 το συσσωμάτωμα επιβραδύνεται, το Σ2 επιταχύνεται
ΣF = m2 .α2 = Τ' => α2 = 5 Ν / 4 kg => a2 = 1,25 m/s2 v2 = a2 . t => t = 1 / 1,25 = 0,8 s
v2 = v1 - a . t => 1= 5 - 5 . t => t = 4/5 sec = 0,8 s
x1 = v1 . t - 0,5 . a1 . t2 = 5 . 0,8 - 0,5 . 5 . 0,82 => x1 = 4 - 1,6 => x1 = 2,4 m
x2 = 0,5 . a2 . t2 = 0,5 . 1,25 . 0,82 => x2 = 0,4 m
το συσσωμάτωμα μετακινήθηκε πάνω στο Σ2 κατά x1 - x2 = 2 m
7. Σώμα Σ1 μάζας m1 κινούμενο πάνω σε λείο οριζόντιο δάπεδο με ταχύτητα υ1 συγκρούεται κεντρικά με ακίνητο σώμα Σ2. Αμέσως μετά την κρούση τα δύο σώματα κινούνται με ταχύτητες ίσου μέτρου υ1' = υ2' = υ1 / 2 , επί της ίδιας ευθείας. Λόγω της κρούσης η κινητική ενέργεια του συστήματος των συγκρουομένων σωμάτων :
(α) παραμένει σταθερή (β) υποδιπλασιάζεται (γ) υποτετραπλασιάζεται
Α) αν η κρούση είναι κεντρική και μετά κινούνται προς την ίδια κατεύθυνση :
p1 = p1' + p2' => m1 . v1 = m1 . v1 / 2 + m2 . v1 / 2 => m1 = m1 / 2 + m2 / 2 => m1 = m2
Kαρχ = ½ . m1 . v12
Kτελ = ½ . m1 .(v1 / 2)2 + ½ . m2 .(v1 / 2)2 = 2 . ½ . m1 . v12 / 4 = ½ . m1 . v12 / 2 = ½ . Kαρχ
Β) αν η κρούση είναι κεντρική και μετά κινούνται προς αντίθετη κατεύθυνση :
p1 = p1' + p2' => m1 . v1 = m1 . ( - v1 / 2 ) + m2 . v1 / 2 => m1 = - m1 / 2 + m2 / 2 => 3.m1 = m2
Kαρχ = ½ . m1 . v12
Kτελ = ½ . m1 .( - v1 / 2)2 + ½ . m2 .(v1 / 2)2 = ½ . m1 . v12 / 4 + ½ . 3.m1 . v12 / 4 =
4 . ½ . m1 . v12 / 4 = ½ . m1 . v12 = Kαρχ
8. Σώμα μάζας m κινούμενο πάνω σε λείο οριζόντιο δάπεδο με ταχύτητα μέτρου υ προσπίπτει κάθετα σε κατακόρυφο τοίχο και ανακλάται με ταχύτητα μέτρου υ'. Αν το μέτρο της μεταβολής της ορμής του σώματος είναι ίσο με 4/3.m.υ τόε η μεταβολή της κινητικής ενέργειας ισούται με :
(α) 0 (β) - 4/9. m.υ2 (γ) - 16/9. m.υ2
Δp = pτελ - pαρχ => Δp = - m.v' - m.v => - 4/3 m v = - m.v' - m.v => - 1/3 v = v'
ΔΚ = ½ . m. (- v/3)2 - ½ . m. v2 => ΔΚ = - 4/9 . m. v2
9. Σημειακή σφαίρα Σ1 μάζας m1 κινούμενη πάνω σε λείο οριζόντιο δάπεδο με ταχύτητα υ1 συγκρούεται κεντρικά - ελαστικά με ακίνητη σημειακή σφαίρα Σ2 μάζας m2. Λόγω της κρούσης η ταχύτητα της σφαίρας Σ1 αλλάζει φορά και το μέτρο της μειώνεται κατά 20%. Μετά την κρούση η σφαίρα Σ2 κινείται πάνω στο οριζόντιο δάπεδο με ταχύτητα μέτρου :
(α) 0,2 υ1 (β) υ1 (γ) 1,8 υ1
v1' = v1 . (m1 - m2) / (m1 + m2) => - 0,8 v1 = v1 . (m1 - m2) / (m1 + m2) => - 0,8 .(m1 + m2) = m1 - m2 => - 0,8 .m1 - 0,8 .m2 = m1 - m2 => 0,2 m2 = 1,8 m1 => m2 = 9 m1
v2' = 2 m1 v1 / (m1 + m2) = 2 m1 v1 / (m1 + 9 m1 ) = 0,2 v1
10. Σφαίρα μάζας m προσκρούει ελαστικά και πλάγια σε λείο κατακόρυφο τοίχο υπό γωνία 60°. Αν η ορμή της σφαίρας ακριβώς πριν την κρούση έχει μέτρο p τότε η μεταβολή της ορμής λόγω της κρούσης θα έχει μέτρο :
(α) p (β) 2p (γ) μηδέν
Αν η χρονική διάρκεια της κρούσης είναι Δt = 10-3 s και p = 100 kg.m/s υπολογίστε το μέτρο της δύναμης που ασκείται στον τοίχο από τη σφαίρα.
Δpx = 0 Δpy = - 2 py = - 2 p συν60° = - 2 p 0,5 = - p => |Δpy|= p
συνολικά |Δp|= p
F = |Δp|/ Δt = p / Δt = 100 kg.m/s 10-3 s = 105 N
11. Σφαίρα μάζας m κινούμενη σε λείο οριζόντιο επίπεδο έχοντας ορμή μέτρου p συγκρούεται κεντρικά πλαστικά με ακίνητο σώμα μάζας 2m Η θερμότητα που αναπτύχθηκε κατά την κρούση είναι :
(α) p2 / 2m (β) p2 / 3m (γ) p2 / 4m
διατήρηση ορμής : p = 3m υ => υ = p / 3m
ΔΚ = Κτελ - Καρχ = ½ υ2 3m - p2 / 2m = ½ (p / 3m) 2 3m - p2 / 2m =
= ½ ( p2 / 9m2 ) 3m - p2 / 2m = ½ p2 / 3m - p2 / 2m = p2 / 6m - 3p2 / 6m = p2 / 3m
12. Σώμα μάζας m1 κινείται με ταχύτητα υ1 = +5 m/s και συγκρούεται ελαστικά με προπορευόμενο σώμα μάζας m2 το οποίο κινείται με ταχύτητα υ2 = +3 m/s. Η τιμή της παράστασης υ1' - υ2' ισούται με : +8 m/s +2 m/s -2 m/s -8 m/s
v1' - v2' = v1 (m1 - m2)/(m1 + m2) + 2 v2 m2 /(m1 + m2) - v2 (m2 - m1)/(m1 + m2) - 2 v1 m1 /(m1 + m2) =
5 (m1 - m2)/(m1 + m2) + 2 3 m2 /(m1 + m2) - 3 (m2 - m1)/(m1 + m2) - 2 5 m1 /(m1 + m2) =
{ - 2m2 - 2m1 } /(m1 + m2) = - 2 m/s
13. Δύο σφαιρίδια Σ1 και Σ2 με μάζες m1 , m2 αντίστοιχα κινούνται πάνω σε λείο οριζόντιο επίπεδο με ταχύτητες υ1 και υ2 ίδιου μέτρου υ0 συγκρούονται κεντρικά - ελαστικά. Μετά την κρούση το Σ2 παραμένει ακίνητο. Το Σ1 κινείται με ταχύτητα που έχει κατεύθυνση :
(α) αντίθετη της υ1 και μέτρο ίσο με υ0
(β) ίδια με την υ1 και μέτρο ίσο με 2υ0
(γ) αντίθετη της υ1 και μέτρο ίσο με 2υ0
v2' = 0 => v2 (m2 - m1) / (m2 + m1) + 2 v1 m1 / (m2 + m1) = 0
=> v0 m2 - v0 m1 + 2 v0 m1 = 0 => m2 + m1 = 0 θα είναι υ1 = - υ0 ή υ2 = - υ0
v2' = 0 => v2 (m2 - m1) / (m2 + m1) + 2 v1 m1 / (m2 + m1) = 0
=> v0 m2 - v0 m1 + 2 (- v0 ) m1 = 0 => m2 - m1 - 2 m1 = 0 => m2 = 3 m1
ή
v2' = 0 => v2 (m2 - m1) / (m2 + m1) + 2 v1 m1 / (m2 + m1) = 0
=> - v0 m2 + v0 m1 + 2 v0 m1 = 0 => - m2 + m1 + 2 m1 = 0 => m2 = 3 m1
οπότε έχουμε υ1' = v1 (m1 - m2) / (m1 + m2) + 2 v2 m2 / (m1 + m2) =
= v0 (m1 - 3m1) / (m1 + 3m1) + 2 ( - v0 ) 3m1 / (m1 + 3m1) =
= v0 ( - 2m1) / 4m1 + 2 ( - v0 ) 3m1 / 4m1 =
= - v0 / 2 - v0 3/2 = - 2 υ0 επειδή υ1 = υ0 άρα (γ)
ή αλλιώς :
οπότε έχουμε υ1' = v1 (m1 - m2) / (m1 + m2) + 2 v2 m2 / (m1 + m2) =
= - v0 (m1 - 3m1) / (m1 + 3m1) + 2 v0 3m1 / (m1 + 3m1) =
= - v0 ( - 2m1) / 4m1 + 2 v0 3m1 / 4m1 =
= + v0 / 2 + v0 3/2 = + 2 υ0 επειδή υ1 = - υ0 άρα (γ)
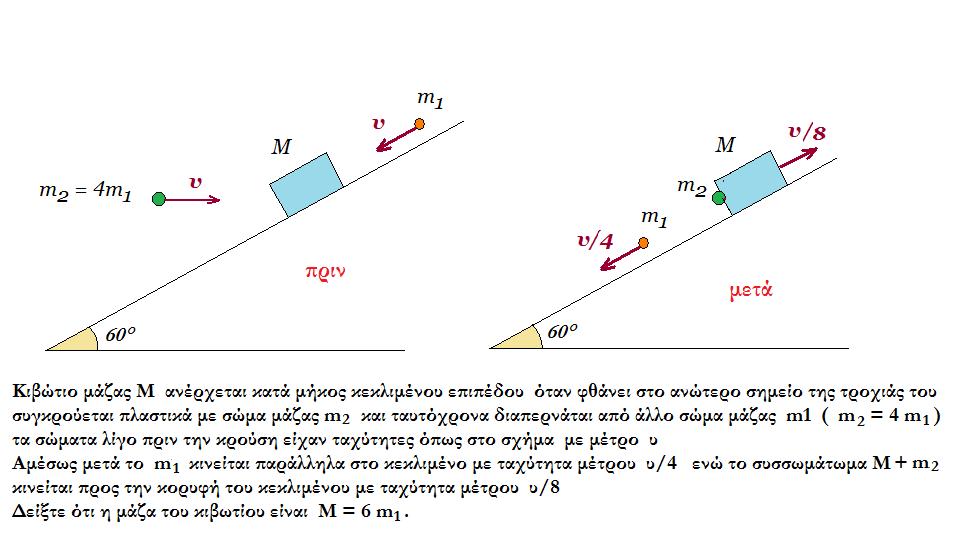
14.
15. Από το εσωτερικό άκρο Α ενός ημισφαιρίου ακτίνας R αφήνεται ελεύθερη μάζα m1 αμελητέων διαστάσεων. Στο κατώτατο σημείο Γ του ημισφαιρίου είναι ακίνητη μια πανομοιότυπη μάζα m2 (m1 = m2 = m) αμελητέων διαστάσεων. Οι τριβές θεωρούνται αμελητέες.
Α. Η μάζα m1 συγκρούεται με τη μάζα m2 κεντρικά και ελαστικά. Μετά την κρούση η μάζα m2 θα ανέλθει σε ύψος Η ως προς το κατώτατο σημείο του ημισφαιρίου ίσο με:
α) R/4 β) R γ) 3R/2
Β. Η μάζα m1 συγκρούεται με τη μάζα m2 μετωπικά και πλαστικά. Μετά την κρούση το συσσωμάτωμα θα ανέλθει σε ύψος h ως προς το κατώτατο σημείο του ημισφαιρίου ίσο με:
α) R/4 β) R γ) 3R/2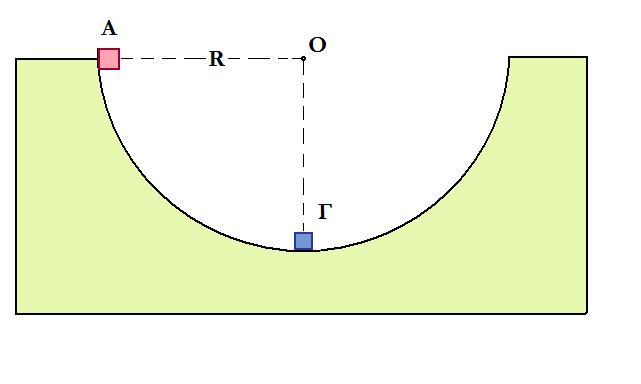
½ m1 v12 = m1 g R => v12 = 2 g R
(Α) η κρούση είναι κεντρική - ελαστική τα σώματα έχουν ίσες μάζες άρα ανταλλάσουν ταχύτητες και επειδή το Σ2 αρχικά είναι ακίνητο έχουμε : υ1' = υ2 = 0 και υ2' = υ1 = ( 2 g R )½ μετά έχουμε: ½ m2 (v2')2 = m2 g Η => (v2')2 = 2 g Η => 2 g R = 2 g Η => Η = R
(Β) η κρούση είναι κεντρική - πλαστική τα σώματα έχουν ίσες μάζες
m1 v1 = (m1 + m2) u => m v1 = 2 m u => u = v1 / 2 = ½ ( 2 g R )½ μετά έχουμε: ½ 2 m u2 = 2 m g h => u2 = 2 g h => 1/4 2 g R = 2 g h => h = R/4
16. Μια µικρή σφαίρα µάζας m1 συγκρούεται µετωπικά και ελαστικά µε ακίνητη µικρή σφαίρα µάζας m2. Μετά την κρούση οι σφαίρες κινούνται µε αντίθετες ταχύτητες. Ο λόγος των µαζών m1/m2 των δύο σφαιρών είναι:
α. 1 β. 1/3 γ. 1/2
Να αιτιολογήσετε την απάντησή σας.
Αν η κρούση είναι κεντρική - πλαστική τότε ο λόγος Κτελ / Καρχ της τελικής κινητικής ενέργειας προς την αρχική είναι :
α. 1/4 β. 1/3 γ. 1/2
ελαστική κρούση : v1' = v1 (m1 - m2)/(m1 + m2) v2' = 2 v1 m1 /(m1 + m2)
v1' = - v2' => v1 (m1 - m2)/(m1 + m2) = - 2 v1 m1 /(m1 + m2) => m1 - m2 = - 2 m1 =>
=> 3 m1 = m2 => m1/m2 = 1/3
πλαστική κρούση : m1 v1 = (m1 + m2) u => u = m1 v1 / (m1 + 3m1) = m1 v1 / 4m1 = v1 / 4
Kτελ = ½ (m1 + m2) u2 = ½ 4m1 v12/16 = m1 v12/8 => Kτελ = Καρχ / 4
17. Oμογενής ράβδος μήκους l=1,5 m και μάζας M=6 Kg ηρεμεί πάνω σε λεία οριζόντια επιφάνεια. Ένα σφαιρίδιο μάζας m κινείται οριζόντια με ταχύτητα υ=8 m/s κάθετη στη ράβδο και συγκρούεται ελαστικά με τη ράβδο σε απόσταση d=L/6 από το μέσο της.
Γ.1. Πόση πρέπει να είναι η μάζα m του σφαιριδίου, ώστε να αποκτήσει αντίρροπη ταχύτητα αμέσως μετά την ελαστική κρούση με μέτρο υ'=υ/2;
Δίνεται η ροπή αδράνειας ράβδου ως προς άξονα που διέρχεται από το μέσο της και είναι κάθετος σε αυτή: Icm = 1/12 M l2
Γ.2. Μετά την κρούση περνά χρονικό διάστημα ∆t = π/12 s. Εκείνη τη στιγμή να υπολογίσετε την ταχύτητα 𝜐𝛢 και την επιτάχυνση 𝛼𝛢 του άκρου Α της ράβδου.
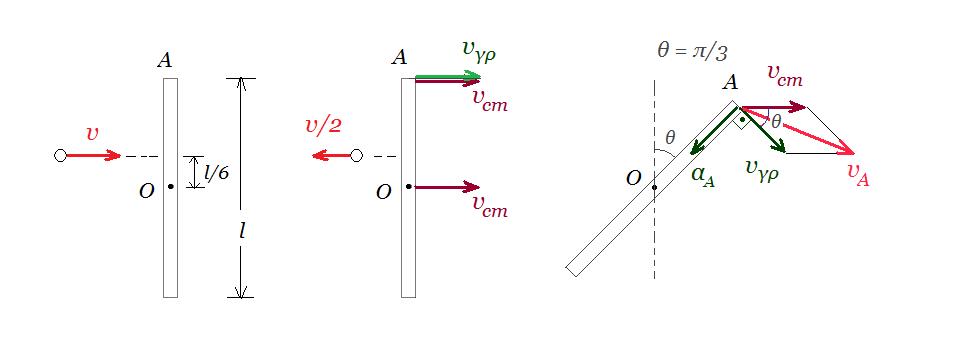
Γ.1.
διατήρηση ορμής : pαρχ = pτελ => m υ = - m υ/2 + Μ υcm => 3/2 m υ = Μ υcm (1)
διατήρηση στροφορμής : Lαρχ = Lτελ => m υ d = Icm ω => m υ l/6 = - m υ/2 l/6 + 1/12 M l2 ω => 3/2 m υ l/6 = 1/12 M l2 ω => 3 m υ = M l ω = Μ 2υcm (2) διότι υcm = l/2 ω
διατήρηση ενέργειας : Καρχ = Κτελ => ½ m υ2 = ½ m (υ/2)2 + ½ Μ υcm2 + ½ Icm ω2 =>
=> m υ2 - m (υ/2)2 = Μ υcm2 + 1/12 M l2 ω2 => 3/4 m υ2 = Μ υcm2 + 1/12 M 4 υcm2 =>
=> 3/4 m υ2 = 4/3 M υcm2 (3)
(3) / (1) => 1/2 υ = 4/3 υcm => υcm = 3/8 υ = 3/8 8 m/s => vcm = 3 m/s
ω = 2υcm /l = 2 3m/s / 1,5m => ω = 4 rad/s
(2) => 3 m υ = Μ 2υcm => 3 m 8 = 6 2 3 => m = 1,5 kg
Γ.2.
θ = ω t => θ = 4 rad/s π/12 s = π/3 rad γραμμική ταχύτητα : υγρ = ω l/2 = 4 1,5/2 = 3 m/s
v(A)2 = vcm2 + vγρ2 + 2 vcm vγρ συνπ/3 = 32 + 32 + 2 3 3 ½ = 3 32 => υ(Α) = 3 Φ3 m/s
κεντρομόλος επιτάχυνση : α(Α) = vγρ2 / l/2 = 32 / 1,5/2 = 12 m/s2
18. Δύο ομογενείς ελαστικές πρισματικές ράβδοι με αμελητέο πλάτος, η ΟΑ και η ΟΒ, έχουν τις ίδιες ακριβώς διαστάσεις και μάζες αντίστοιχα Μ1 = 1kg και Μ2 = 3kg. Το μήκος κάθε ράβδου είναι l = 1,2 m και οι δύο ράβδοι μπορούν (λόγω του αμελητέου πλάτους τους) να στρέφονται χωρίς τριβές στο ίδιο κατακόρυφο επίπεδο γύρω από οριζόντιο άξονα που περνά από το κοινό τους άκρο Ο και είναι κάθετος στη διεύθυνσή τους. Κρατάμε αρχικά τις ράβδους στην οριζόντια διεύθυνση (1) και τις αφήνουμε ελεύθερες ταυτόχρονα χωρίς αρχική ταχύτητα, οπότε κάποια στιγμή οι ράβδοι συγκρούονται ελαστικά.
α. Να εκφράσετε την γωνιακή ταχύτητα της ράβδου συναρτήσει της γωνίας θ.
β. Θεωρώντας ότι η κρούση των δύο ράβδων αρχίζει και τελειώνει στην κατακόρυφη διεύθυνση (δηλ. δε στρέφονται όσο διαρκεί η κρούση τους), να υπολογίσετε τα μέτρα των γωνιακών τους ταχυτήτων αμέσως μετά την κρούση.
γ. Ποια είναι η μέση (κατά μέτρο) ροπή που δέχθηκε η ράβδος ΟΑ κατά την κρούση, αν η χρονική διάρκεια της κρούσης αυτής είναι Δt = 0,05 s.
δ. Να εξετάσετε αν, μετά την κρούση, η ράβδος ΟΑ θα πραγματοποιήσει, ανακύκλωση.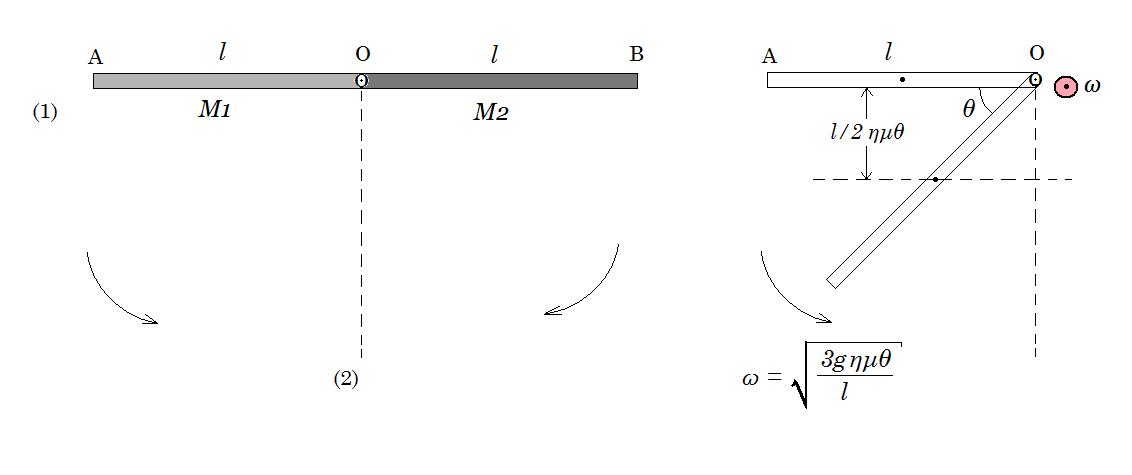 
Α) διατήρηση ενέργειας : Καρχ + Uαρχ = Κτελ + Uτελ => 0 + M g l/2 ημθ = ½ Icm ω2 + 0 =>
=> M g l/2 ημθ = ½ 1/3 M l2 ω2 => g ημθ = 1/3 l ω2 => ω2 = 3gημθ/l => ω = (3gημθ/l)½
Β) διατήρηση ενέργειας : Καρχ + Uαρχ = Κτελ + Uτελ => 0 + M g l/2 = ½ Icm ω2 + 0 =>
=> M g l/2 = ½ 1/3 M l2 ω2 => g = 1/3 l ω2 => ω2 = 3g/l => ω = (3g/l)½ = 5 rad/s (1)
διατήρηση στροφορμής : Lαρχ = Lτελ => I1 ω1 + I2 ω2 = I1 ω1' + I2 ω2' =>
=> 1/3 M1 l2 ω1 - 1/3 M2 l2 ω2 = 1/3 M1 l2 ω1' + 1/3 M2 l2 ω2' =>
=> 1 (3g / l)½ - 3 (3g / l)½ = 1 ω1' + 3 ω2' =>
=> - 2 (3g / l)½ = ω1' + 3 ω2' (2)
η (2)2 => 4 3g / l = ω1'2 + 9 ω2'2 + 6 ω1' ω2' (3)
διατήρηση ενέργειας : ½ I1 ω12 + ½ I2 ω22 = ½ I1 ω1'2 + ½ I2 ω2'2 =>
=> ½ 1/3 M1 l2 ω12 + ½ 1/3 M2 l2 ω22 = ½ 1/3 M1 l2 ω1'2 + ½ 1/3 M2 l2 ω2'2 =>
=> 1 3g/l + 3 3g/l = 1 ω1'2 + 3 ω2'2 =>
=> 12g/l = ω1'2 + 3 ω2'2 (4)
(3) - (4) => 0 = 6 ω2'2 + 6 ω1' ω2' => ω2' = 0 ή ω1' = - ω2'
εάν ω1' = - ω2' τότε η (2) => - 2 (3g / l)½ = - ω2' + 3 ω2' =>
=> - 2 (3g / l)½ = - 2 ω2' => ω2' = (3g / l)½ = ω2 αρχική γωνιακή απορρίπτεται
εάν ω2' = 0 τότε η (2) => ω1' = - 2 (3g/l)½ = - 10 rad/s δεκτές λύσεις
Γ) Στ1 = ΔL1 / Δt = (L1' - L1) / Δt = I1 ( ω1' - ω1 ) / Δt = 1/3 M1 l2 ( ω1' - ω1 ) / Δt =
= 1/3 1 1,22 ( -10 - 5 ) / 0,05 = - 144 Ν m
Δ) διατήρηση ενέργειας : ½ I1 (ω1')2 = M1 g l + ½ I1 (ω1'')2 =>
=> ½ 1/3 M1 l2 12g / l = M1 g l + ½ 1/3 M1 l2 (ω1'')2 =>
=> 2 l g = g l + ½ 1/3 l2 ω1''2 => l g = ½ 1/3 l2 (ω1'')2 => (ω1'')2 = 6 g/l = 5 Φ2 rad/s
η ράβδος (1) θα κάνει ανακύκλωση και όταν διέρχεται από την ανώτερη θέση της τροχιάς της έχει γωνιακή ταχύτητα ω1'' = (6g/l)½