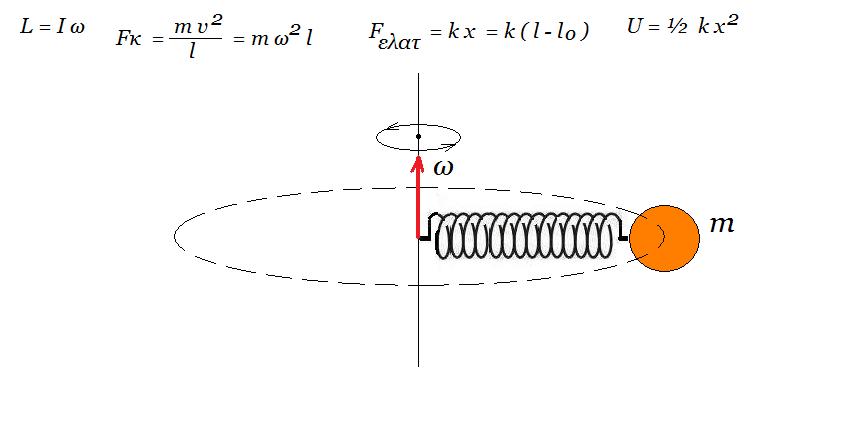
L = m v l = m ω l² = Ι ω      Fκ = m v²/ l = m ω² l        F_ελατ = k x  = k ( l - l₀ )        U = ½  k x²  

 Fκ = F_ελατ =>   m ω² l  = k ( l - l₀ )  =>  l  =  k l₀ / ( k - m ω² ) 

όταν  ω ® 0  τότε    l  ®  l₀   φυσικό μήκος ελατηρίου  

όταν  ω ® (k/m)^½   τότε   l  ®  ¥

x = l - l₀  = k l₀ / ( k - m ω² ) - l₀  = k l₀ / ( k - m ω² )  -  l₀ =  k l₀ /( k - m ω² )  -  l₀ ( k - m ω² )/( k - m ω² )

=>   x =  l - l₀  =  l₀ m ω² / ( k - m ω² )  

 U = ½  k x² =  ½  k ( l - l₀ )² =  ½  k l₀² m² ω⁴ / ( k - m ω² )²  

όταν  ω ® 0  τότε   U ®  0   το ελατήριο έχει το φυσικό του μήκος  

όταν  ω ® (k/m)^½   τότε   U  ®  ¥