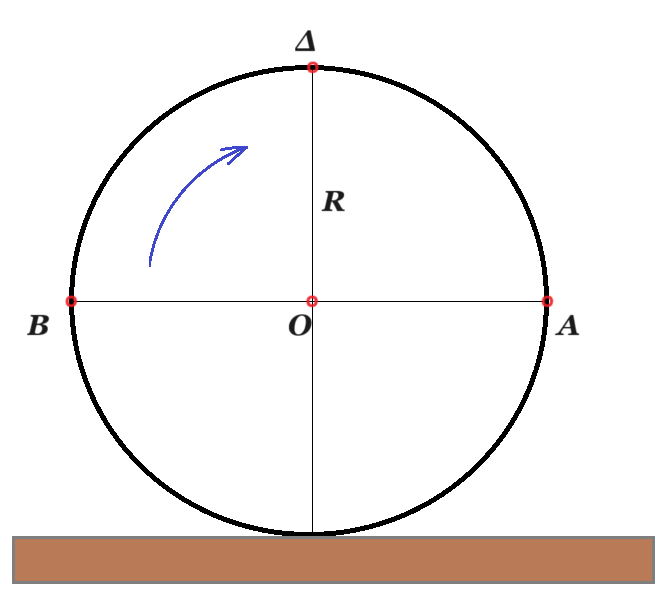
Τροχός έχει ακτίνα R και ηρεμεί με το επίπεδό του κατακόρυφο.  Την χρονική στιγμή t₀=0 ο τροχός αρχίζει να κυλίεται χωρίς να ολισθαίνει, προς τα δεξιά με σταθερή γωνιακή επιτάχυνση  α_γων.  Κάποια χρονική στιγμή t₁ η ολική επιτάχυνση του σημείου Α της περιφέρειας του τροχού, το οποίο απέχει από το έδαφος απόσταση ίση με την ακτίνα του τροχού, έχει διεύθυνση κατακόρυφη με φορά προς τα κάτω.  Την στιγμή αυτή ο λόγος των μέτρων των ολικών επιταχύνσεων των σημείων Β, που είναι αντιδιαμετρικό του Α και του υψηλότερου σημείου Δ του τροχού έχει τιμή:  

α)  1          β)  √2           γ)  1/2

33.   Ένα ακίνητο στερεό αποτελείται από δύο κατακόρυφους ομοαξονικούς κυλίνδρους κολλημένους μεταξύ τους, ακτίνων R και 3R. Το στερεό μπορεί να στρέφεται γύρω από τον κοινό οριζόντιο άξονα των δύο κυλίνδρων ως ένα σώμα. Στην περιφέρεια του κυλίνδρου ακτίνας R έχουμε τυλίξει ένα λεπτό νήμα. Τραβάμε το νήμα οριζόντια από το άκρο του Α με επιτάχυνση μέτρου α_Α = 4 m/s²   ξετυλίγοντάς το χωρίς το νήμα να ολισθαίνει στην επιφάνεια του κυλίνδρου.  Τη χρονική στιγμή t₀=0 το στερεό αρχίζει να κυλίεται στο οριζόντιο έδαφος χωρίς να ολισθαίνει με σταθερή γωνιακή επιτάχυνση.
Δ1.   Να βρείτε την επιτάχυνση του κέντρου μάζας του στερεού και την εφαπτομενική επιτάχυνση του σημείου Ε.
Δ2.   Αν R = 0,1 m, να βρείτε τη γωνιακή επιτάχυνση του στερεού.
Όταν έχει ξετυλιχτεί νήμα μήκους  l = 8 m, να βρείτε:
Δ3.   πόσο έχει μετακινηθεί το κέντρο μάζας του στερεού και πόσο το άκρο Α του νήματος
Δ4.   πόση είναι η γωνιακή ταχύτητα του στερεού
Δ5.   πόση είναι η ταχύτητα του ανώτερου σημείου κάθε κυλίνδρου.

  σημείο Γ στιγμιαία ακίνητο :   υ_cm = ω R   =>   α_cm = α_γων R     

επειδή η συνολική επιτάχυνση του σημείου Α είναι κατακόρυφη προς τα κάτω  άρα  α_cm = α_κ = v²/R  =  ω²R 

σημείο Β :  α_Β² = ( α_cm + α_κ )² + ( α_γων R )²  = ( α_γων R + α_γων R )² + ( α_γων R )² = 5 (α_γων R)² 

σημείο Δ :  α_Δ²= ( α_cm + α_γων R )² + ( α_κ )²  = ( α_γων R + α_γων R )² + ( α_γων R )² = 5 (α_γων R)² 

  συνεπώς :   α_Β / α_Δ = 1      

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

33.

Δ1.     F R +  Τ 3R = I  α_γων        F -  Τ  =  m a_cm               a_cm =  α_γων 3R    

 a_A =  a_Δ  =  a_cm + α_γων R =  α_γων 3R + α_γων R =>  a_A = α_γων 4R =>  4 m/s² = α_γων 4R  =>  1 m/s² = α_γων R

  a_cm =  α_γων 3R  = 3 m/s²        και    α_Ε  = a_cm + α_γων 3R =  α_γων 3R  + α_γων 3R  =  6 m/s²     

Δ2. 1 m/s²  =  α_γων R  =>  1 m/s²  =  α_γων 0,1 m  => α_γων  =  10 rad/s²    

Δ3.  μήκος νήματος = μήκος τόξου    l = s = R θ  =>  8 m =  0,1 m  θ  =>   θ = 80 rad          

  θ = ½ α_γων t²  => 80 = ½ 10  t²  => t²  = 16  =>  t = 4 s

  x_cm  = ½ α_cm t²  = ½  3 m/s²  16 s²  = 24 m

  x_A  = ½ α_A t²  = ½  4 m/s²  16 s²  = 32 m  =  24 m + 8 m  =  x_cm + l

Δ4.   ω  = α_γων t  = 10 rad/s²  4 s  = 40 rad/s                 υ_cm = ω 3R = 40 rad/s  0,3 m = 12 m/s  

Δ5.  υ_Δ = υ_cm + ω R  = 12 m/s  + 40 rad/s  0,1 m  =  16 m/s  

   υ_E = υ_cm + ω 3R  = 12 m/s  + 40 rad/s  0,3 m  =  24 m/s