ΘΕΜΑ 30.
Λεπτή ομογενής ράβδου ΑΔ έχει μήκος L=6m και μάζα Μ=4Κg. Η ράβδος είναι αρθρωμένη στο άκρο της Α και ηρεμεί σε οριζόντια θέση με τη βοήθεια αβαρούς μη εκτατού νήματος που το ένα άκρο του είναι προσδεμένο στο σημείο Β της ράβδου, ενώ το άλλο του άκρο στερεωμένο στον κατακόρυφο τοίχο. Το νήμα σχηματίζει γωνία φ με τη ράβδο (ημφ=0,8 και συνφ=0,6) ενώ η απόσταση (ΑΒ)=L/4.
Στο σημείο Γ της ράβδου ισορροπεί ομογενής σφαίρα μάζας m=3Kg και ακτίνας r=0,1m ενώ η απόσταση του κέντρου μάζας της από το άκρο Δ της ράβδου είναι (ΓΔ)=L/3.
Δ1. Να υπολογίσετε το μέτρο της δύναμης που ασκείται στη ράβδο από την άρθρωση.
Τη χρονική στιγμή t=0 ασκείται στο ανώτερο σημείο της σφαίρας σταθερή οριζόντια δύναμη μέτρου F=2,1N, με φορά προς τα δεξιά. Η σφαίρα αρχίζει να κυλίεται χωρίς να ολισθαίνει πάνω στη ράβδο.
Δ2. Να υπολογίσετε το μέτρο της γωνιακής επιτάχυνσης της σφαίρας.
Η ροπή αδράνειας της σφαίρας ως προς άξονα που διέρχεται από το κέντρο μάζας της υπολογίζεται από τη σχέση: I = 2/5 m r2
Δ3. Να υπολογίσετε το μέτρο της γωνιακής ταχύτητας της σφαίρας τη στιγμή t1 κατά την οποία εγκαταλείπει τη ράβδο.
Δ4. Να υπολογίσετε τον αριθμό των περιστροφών που εκτελεί η σφαίρα σε χρονικό διάστημα Δt=1s από τη στιγμή που εγκατέλειψε τη ράβδο , καθώς και την ταχύτητα που έχει αποκτήσει το κέντρο μάζας της σε αυτό το χρονικό διάστημα.
Δίνεται η επιτάχυνση της βαρύτητας g=10m/s2.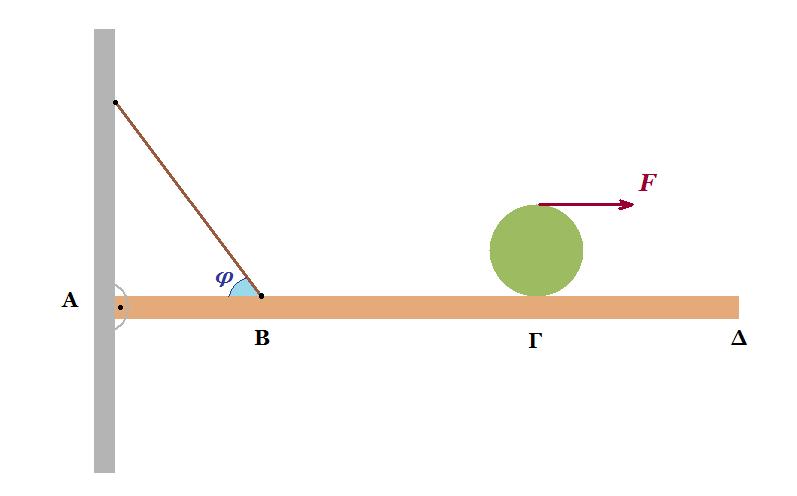
ροπές ως προς Α : Μg L/2 + mg 2L/3 - FBy L/4 = 0 => 40 3 + 30 4 = FBy 1,5 =>
=> FBy = 160 N
FBx = FBy / εφφ => FBx = 160 N / (4/3) = 120 N
FAx = FBx = 120 N
ΣFy = 0 => FAy + FBy = Mg + N => FAy + 160 = 40 + 30 => FAy = - 90 N κατακόρυφη προς τα κάτω
FA2 = FAx2 + FAy2 => FA2 = 1202 + 902 = 14400 + 8100 = 22500 => FA = 150 N
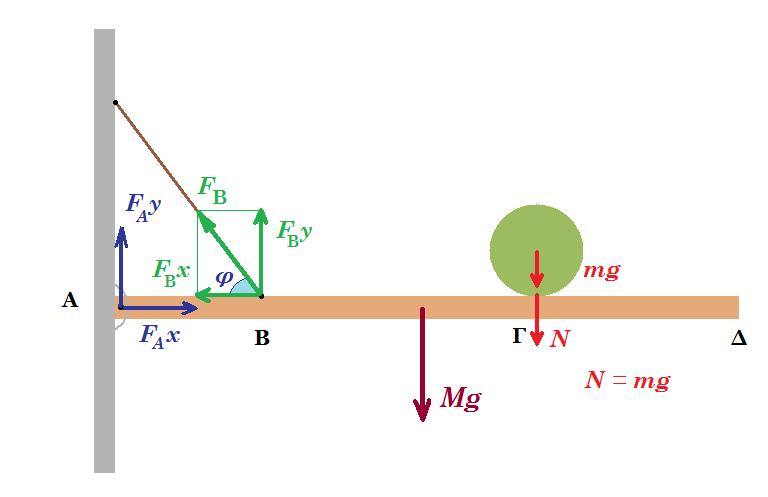
έστω η τριβή αντίρροπη της F : ΣF = m a => F - T = m α (1)
Στ(Κ) = Ι αγων => ( F + T ) r = 2/5 m r2 αγων => F + T = 2/5 m r αγων =>
=> F + T = 2/5 m α (2)
(1) + (2) => 2 F = 7/5 m a => a = 10F / 7m = 21/21 = 1 m/s2 αγων = a / r = 10 rad/s2
(2) - (1) => 2 T = - 3/5 m a => T = - 3/10 m a = - 3/10 3 1 = - 0,9 Ν T , F ομόρροπες
x = ½ a t2 => L/3 = 6/3 = ½ 1 t2 => t2 = 4 => t = 2 s v0 = a t = 1 2 = 2 m/s
ω = αγων t = 10 2 = 20 rad/s
η γωνιακή ταχύτητα της σφαίρας παραμένει σταθερή διότι η μόνη δύναμη που ασκείται σ'αυτήν είναι το βάρος της που η ροπή της ως προς το κέντρο της είναι μηδέν έτσι θ = ω t = 20 1 = 20 rad και Ν = 20 / 2π = 10 / π περιστροφές
υ2 = υ02 + (g t) 2 = 22 + 102 = 104 m2/s2
M g h + ½ M υ2 + 0,5 I(Κ) ω2 = ½ M υ'2 + 0,5 I(Κ) ω2
3 10 h + ½ 3 22 = ½ 3 104 => 20 h = 104 - 4 = 100 => h = 5 m = ½ 10 12 = ½ g t2
ΘΕΜΑ 14.
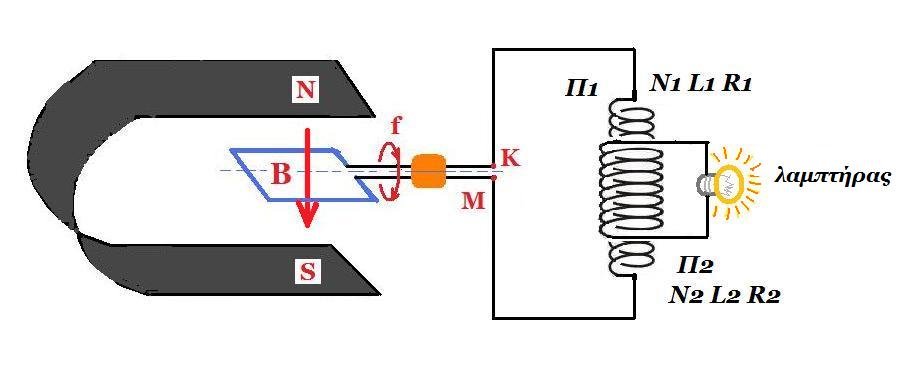
Τα άκρα πηνίου Π1 συνδέονται με στρεφόμενο πλαίσιο Ν = 10 περιελίξεων, εμβαδού επιφάνειας Α=0,1m2 (κάθε μίας), το οποίο περιστρέφεται με σταθερή συχνότητα f, μέσα σε ομογενές μαγνητικό πεδίο εντάσεως Β = 0,1ΧΦ2 T. Το πηνίο Π1 έχει Ν1 = 1000 σπείρες, μήκος L1 = 0,2m και αντίσταση R1=10Ω. Γύρω απο το μέσον του πηνίου Π1 τυλίγουμε πηνίο Π2 της ιδίας ακτίνας r = 0,1 m (για κάθε σπείρα), που έχει Ν2 = 200 σπείρες, μήκος L2 = 0,1 m και αντίσταση R2 = 20 Ω. Τα άκρα του πηνίου Π2 συνδέονται με λαμπτήρα με χαρακτηριστικά: <20V, 80W>. Με ποια συχνότητα f πρέπει να περιστρέφεται το πλαίσιο για να φωτοβολεί κανονικά ο λαμτήρας;
P = V i => i = P/V = 80W / 20V = 4A = Ιεν Ι0 = 4ΧΦ2 Α Rλ = V / i = 20V / 4A => Rλ = 5Ω
Εεπαγ(1) = -Ν.|ΔΦ|/Δt, Εεπαγ(1) = - Ν.Φ'(t) = - Ν.[B.A.συν(ω.t)]' = -Ν.B.A.ω.(-ημωt) = Ν.B.A.2πf.ημ(2πf.t) = 10 . 0,1ΧΦ2 .0,1 . 2πf . ημ(2πf.t) => Εεπαγ(1) = 0,1ΧΦ2 . 2πf . ημ(2πf.t)
Ι1 = Εεπαγ(1) / R1 = 0,01ΧΦ2 . 2πf . ημ(2πf.t)
Β1 = μο Ν1 Ι1 / L1 => Β1 = 4π.10-7 (1000 / 0,2) 0,01ΧΦ2 2πf ημ(2πf.t) = 2π.10-5 Φ2 2πf ημ(2πf.t)
S=π.r2 = π.10-2m2
Φ2 = Β1 . S . N2 => Φ2 = 2π.10-5 ΧΦ2 2πf ημ(2πf.t) . π.10-2 . 200 = 4ΧΦ2 . 10-4 2πf ημ(2πf.t)
Εεπαγ(2) = - Φ2'(t) => Εεπαγ(2) = - 4ΧΦ2 . 10-4 . (2πf)2 . συν(2πf.t)
Ι2 = Εεπαγ(2) / (R2 + RΛ) => Ι2 = - 4ΧΦ2 . 10-4 . (2πf)2 . συν(2πf.t) / (20 + 5)
Ι0 = 4.2½ .10-4 . (2πf)2 / 25 = 4.2½ Α => (2πf)2 = 25 . 104 => 2πf = 500 => f = 250/π Hz


