

Θέμα 9.
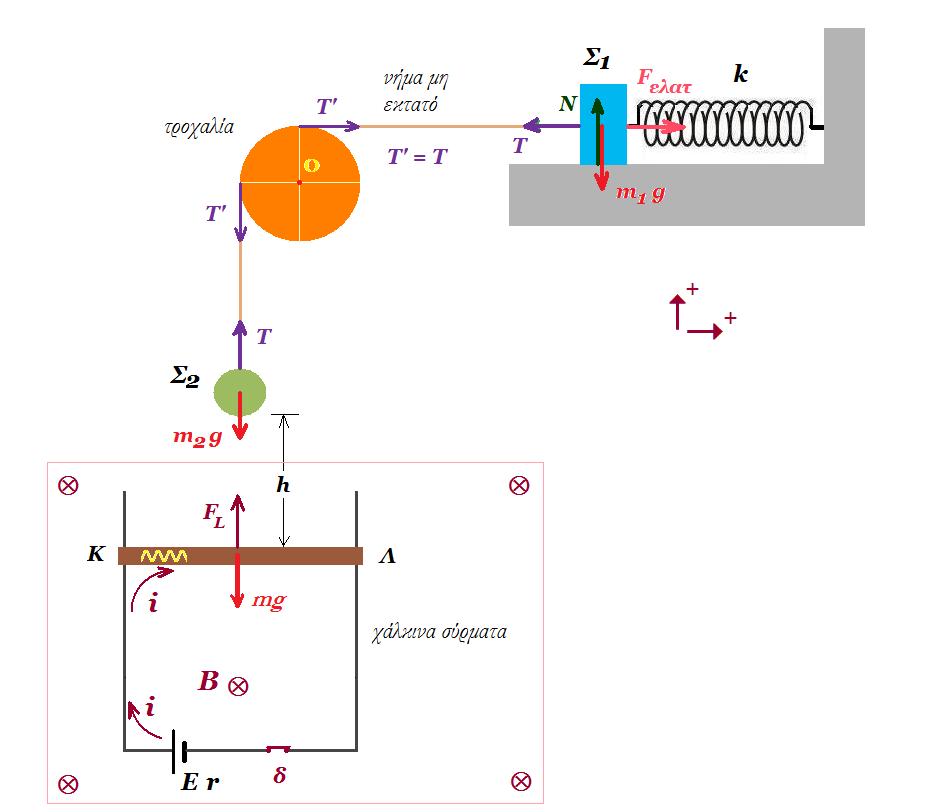
Η διάταξη του σχήματος είναι σε κατακόρυφο επίπεδο και όλα τα σώματα είναι σε κατάσταση ισορροπίας. E = 20 V, r = 3 Ω, R = 7 Ω, m = 0,1 kg, l = 1 m, m1 = 0,5 kg, m2 = 0,1 kg, k = 50 N/m, h = 1,8 m
(α) Υπολογίστε τις δυνάμεις που ασκούνται στα σώματα Σ1 , Σ2 και στη ράβδο ΚΛ και την ένταση Β του ομογενούς μαγνητικού πεδίου.
Τη χρονική στιγμή t = 0 κόβουμε το νήμα που συνδέει τα σώματα Σ1 και Σ2 , το Σ1 θα εκτελέσει απλή αρμονική ταλάντωση
(β) εκφράστε σχέση της δύναμης του ελατηρίου συναρτήσει του χρόνου
και το Σ2 θα κάνει ελεύθερη πτώση.
Το Σ2 συγκρούεται κεντρικά - ελαστικά με την ράβδο ΚΛ.
(γ) Μελετήστε την κίνηση τ.ης ράβδου μετά την κρούση.
ισορροπία Σ2 : T = m2 g = 0,1 kg 10 m/s2 => T = 1 N
ισορροπία Σ1 : T = k x1 => 1 Ν = 50 Ν/m x1 => x1 = 0,02 m επιμήκυνση ελατηρίου
νόμος του Ohm για κλειστό κύκλωμα : Ε = i ( R + r ) => 20 V = i ( 7 Ω + 3 Ω ) => i = 2 A
η ράβδος ΚΛ διαρρέεται από ρεύμα και βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο Β συνεπώς δέχεται δύναμη Laplace αντίθετη του βάρους της : FL = m g = 0,1 kg 10 m/s2 => FL = 1 N
FL = B i l => B = 1 N / ( 2 A 1 m ) => B = 0,5 T
τη χρονική στιγμή t = 0 κόβουμε το νήμα που συνδέει τα σώματα Σ1 και Σ2
το Σ1 θα εκτελέσει απλή αρμονική ταλάντωση και το Σ2 θα κάνει ελεύθερη πτώση
το Σ1 θα εκτελέσει απλή αρμονική ταλάντωση :
ω2 = k/m1 = 50 / 0,5 = 100 => ω = 10 rad/s T = 2π/ω = 2π/10 = π/5 s
x(t) = 0,02 ημ(10 t + 3π/2) υ(t) = 0,2 συν(10 t + 3π/2) α(t) = - 2 ημ(10 t + 3π/2)
F(t) = m1 a(t) = - 0,5 2 ημ(10 t + 3π/2) => F(t) = - ημ(10 t + 3π/2) = Fελατ (t)
x(0) = - 0,02 m v(0) = 0 a(0) = - 2 m/s2 Fελατ (0) = 1 N ημ(3π/2) = -1 συν(3π/2) = 0
το Σ2 θα κάνει ελεύθερη πτώση : υ = g t h = ½ g t2 v = (2 g h)½ = (2 10 1,8)½ = 36½ = 6 m/s
η κρούση είναι κεντρική - ελαστική οι μάζες είναι ίσες άρα τα σώματα θα ανταλλάξουν ταχύτητες : το Σ2 ακινητοποιήται στιγμιαία και η ράβδος αποκτά ταχύτητα : v = 6 m/s = v0 με κατεύθυνση κατακόρυφη προς τα κάτω
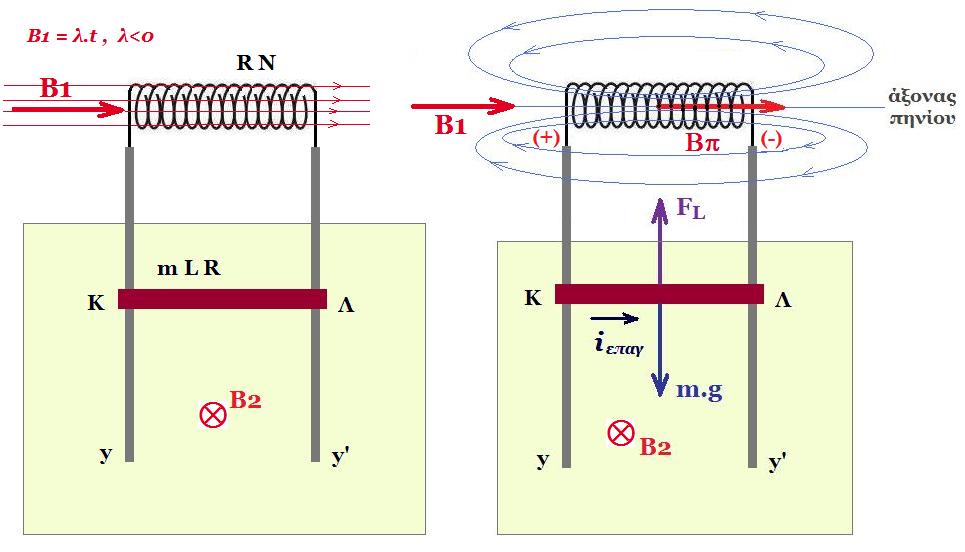
θα χαλάσει η ισορροπία, θα τέμνει δυναμικές γραμμές του μαγνητικού πεδίου, τα ηλεκτρόνιά της δεχόμενα δυνάμεις από την κίνηση μέσα στο μαγνητικό πεδίο κινούνται προς το άκρο Κ που φορτίζεται αρνητικά και το άκρο Λ φορτίζεται θετικά, δηλαδή εμφανίζεται επαγωγική τάση στα άκρα Κ, Λ
νόμος του Ohm για κλειστό κύκλωμα : Ε + Εεπαγ = i ( R + r ) => Ε + Β l v = i ( R + r ) =>
=> i = ( Ε + Β l v ) / ( R + r )
FL = B i l => FL = B l (Ε + Β l v) / (R + r) => FL = 0,5 1 ( 20 + 0,5 1 v ) / 10 =>
FL = 1 + 0,025 v
όσο η κινείται η ράβδος προς τα κάτω περισσότερα ηλεκτρόνια συσσωρεύονται στο άκρο Κ με συνέπεια να αυξάνεται η Εεπαγ
ΣF = m a => m g - FL = m a => 0,1 10 - (1 + 0,025 v) = 0,1 a =>
=> 1 - 1 - 0,025 v = 0,1 a => - 0,025 v = 0,1 dv/dt => - 0,25 dt = dv/v =>
=> - 0,25 t = ln ( v / v0 ) => v / v0 = e-0,25t => v(t) = 6 e-0,25t
a(t) = - 0,25 6 e-0,25t => a(t) = - 1,5 e-0,25t
v(t) = dx/dt = 6 e-0,25t => dx = 6 e-0,25t dt => x(t) = -4 6 { e-0,25t - 1 } =>
=> x(t) = 24 - 24 e-0,25t
Εεπαγ = Β l v = Β l 6 e-0,25t => Εεπαγ (t) = 0,5 6 e-0,25t => Εεπαγ(t) = 3 e-t/4
i = ( Ε + Β l v ) / (R + r) => i(t) = ( 20 + 3 e-0,25t ) / 10 => i(t) = 2 + 0,3 e-t/4
FL = 1 + 0,025 v = 1 + 0,025 6 e-0,25t => FL(t) = 1 + 0,15 e-t/4
dWFL = FL dx => WFL = S0-->t [ 1 + 0,15 e-0,25t ] 6 e-0,25t dt =
= S0-->t [ 1 + 0,15 e-t/4 ] 6 e-t/4 dt = S0-->t [ 6 e-t/4 dt + 0,9 e-t/2 dt ] =
= S0-->t [ 6 (-4) e-t/4 d(-t/4) + 0,9 (-2) e-t/2 d(-t/2) ] =
= - 24 { e-t/4 - 1 } - 1,8 { e-t/2 - 1 } => WFL(t) = 25,8 - 24 e-t/4 - 1,8 e-t/2
P = i2 (R + r) = ( 2 + 0,3 e-t/4 )2 10 => P(t) = 40 + 12 e-t/4 + 0,9 e-t/2
Q = S0-->t P(t) dt = S0-->t { 40 + 12 e-t/4 + 0,9 e-t/2 } dt =
= 40 t - 48 { e-t/4 - 1 } - 1,8 { e-t/2 - 1 } = 40 t - 48 e-t/4 + 48 - 1,8 e-t/2 + 1,8 =>
Q(t) = 40 t - 48 e-t/4 - 1,8 e-t/2 + 49,8