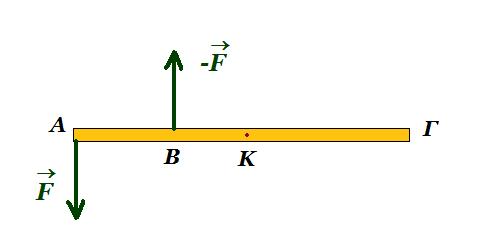
Α1. Η ομογενής και ισοπαχής ράβδος AΓ του σχήματος βρίσκεται εκτός πεδίου βαρύτητας και είναι αρχικά ακίνητη. Οι μόνες δυνάμεις που δέχεται η ράβδος είναι δύο ίδιου μέτρου, αντίθετης φοράς και συνεχώς κάθετες σε αυτή. Η ράβδος περιστρέφεται περί
α. το μέσο του ΑΒ β. το μέσο της, Κ
γ. το σημείο Β δ. το μέσο του ΑΚ
επειδή οι δυνάμεις είναι αντίθετες έχουμε : ΣF = 0 => m a = 0 => a = 0
το σώμα είναι αρχικά ακίνητο : v0 = 0 οπότε v = v0 + a t = 0 + 0 = 0 το σώμα θα μείνει ακίνητο δηλαδή δεν θα μετακινηθεί το κέντρον μάζας του Κ
επειδή οι δυνάμεις είναι αντίθετες δημιουργούν ροπή ζεύγους δυνάμεων : Στ = F Χ (ΑΒ)
συνεπώς η ράβδος θα περιστραφεί περί το μέσον της Κ
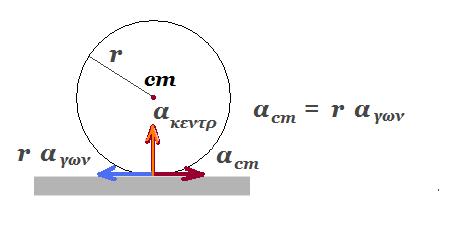
Α2. Στο σχήμα έχουν σχεδιαστεί τα διανύσματα της ταχύτητας και της επιτάχυνσης που έχει το κέντρο ενός τροχού που κυλίεται μια συγκεκριμένη χρονική στιγμή.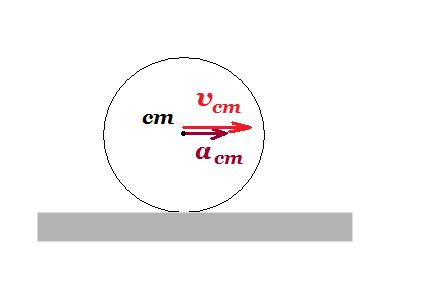 
Την ίδια χρονική στιγμή η συνολική επιτάχυνση, αΣ, που έχει το κατώτερο σημείο του τροχού είναι σωστά σχεδιασμένο στο σχήμα 
(Α) (Β) (Γ) (Δ)
α. Α
β. Β
γ. Γ
δ. Δ
Β. Δύο αστροναύτες μάζας m ο καθένας βρίσκονται στο διάστημα έξω από βαρυτικά πεδία και κρατώντας ένα ιδανικό σχοινί μήκους 2l στρέφονται γύρω από το μέσο (Ο) του σχοινιού εκτελώντας ομαλή κυκλική κίνηση με ταχύτητα μέτρου υ0. Οι αστροναύτες μαζεύοντας το σχοινί πλησιάζουν σε απόσταση x μεταξύ τους, εξακολουθώντας να στρέφονται σε κυκλική τροχιά γύρω από το μέσο (Ο) του νήματος. Αν η περίοδος περιστροφής στη νέα τροχιά υποτετραπλασιάζεται, τότε η ενέργεια που δαπάνησαν οι δύο αστροναύτες για να πλησιάσουν είναι
α) 3/2 m υ02 β) 3 m υ02 γ) 6 m υ02
αρχικά περιστρέφονται με γωνιακή ταχύτητα ω0 = 2π/Τ0
αργότερα ω1 = 2π/Τ1 = 2π / (Τ0/4) => ω1 = 4 ω0
διατήρηση στροφορμής : Lπριν = Lμετά => 2 m υ0 l = 2 m υ1 x/2 => 2 ω0 l2 = ω1 x/2 x =>
=> 4 ω0 l2 = 4 ω0 x2 => l = x
Καρχική = 2 ½ m υ02 = m υ02 = m ω02 l2
Κτελική = 2 ½ m υ12 = 2 ½ m ω12 (x/2)2 = m 16 ω02 (l/2)2 = m 16 ω02 l2 / 4 = 4 m ω02 l2
ΔΚ = 3 m ω02 l2 = 3 m υ02
ΘΕΜΑ Γ
Ένας συμπαγής, ομογενής κύλινδρος έχει μάζα m =2 kg , ακτίνα R =0,2 m και κινείται σε οριζόντιο δάπεδο υπό την επίδραση οριζόντιας δύναμης F η οποία ασκείται στο κέντρο του Κ. Η γωνιακή ταχύτητα του κυλίνδρου και η ταχύτητα του κέντρου μάζας του, σε σχέση με το χρόνο που ασκείται η δύναμη, αποτυπώνονται στα διαγράμματα του σχήματος.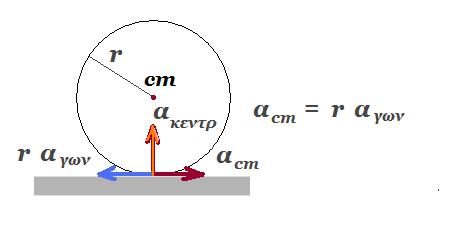
Γ1. Να υπολογίσατε την γωνιακή επιτάχυνση του κυλίνδρου, την επιτάχυνση του κέντρου μάζας και να προσδιορίσετε την κίνηση που εκτελεί ο κύλινδρος συνολικά.
Γ2. Να υπολογίσετε τον συντελεστή τριβής μεταξύ δίσκου και δαπέδου.
Γ3. Να υπολογίσετε το έργο της δύναμης F από την χρονική στιγμή μηδέν ως την στιγμή 2s.
Γ4. Να υπολογίσετε την θερμική ενέργεια που παράγεται από την στιγμή μηδέν ως την στιγμή 2s.
Δίνονται: g = 10 m/s2 και η ροπή αδράνειας του δίσκου Icm = ½ m R2.
α = v / t = 3/2 m/s2 αγων = ω / t = 10/2 = 5 rad/s2 R αγων = 0,2 m 5 rad/s2 = 1 m/s2
παρατηρούμε ότι α > R αγων που σημαίνει ότι ο κύλινδρος δεν κυλίεται μόνο αλλά και ολισθαίνει
Στ(Κ) = Ι(Κ) αγων => Τ R = ½ m R2 αγων => Τ = ½ m R αγων => Τ = ½ 2 0,2 5 => Τ = 1 Ν
T = μ Ν = μ m g => μ = T / (m g) = 1 / ( 2 10 ) => μ = 1/20 = 0,05 συντελεστής τριβής ολισθήσεως
ΣF = m a => F -T = m a => F - 1 = 2 3/2 => F = 4 N
x = ½ α t2 = ½ 3/2 22 => x = 3 m WF = F x = 4 N 3 m => WF = 12 J
Kαρχική = 0 Κτελική = ½ m v2 + ½ ½ m R2 ω2 = ½ 2 32 + 1/4 2 0,22 102 = 9 + 2 = 11 J
Qθερμ = WF - Κτελική = 12 J - 11 J => Qθερμ = 1 J
ο κύλινδρος και κυλίεται και ολισθαίνει
λόγω κυλίσεως διανύει xκυλίσεως = ½ R αγων t2 = ½ 0,2 5 22 = 2 m
λόγω ολισθήσεως διανύει xολισθήσεως = x - xκυλίσεως = 3 m - 2 m = 1 m
η δύναμη τριβής καταναλώνει έργο : WT = T xολισθήσεως = 1 N 1 m => WT = 1 J = Qθερμ