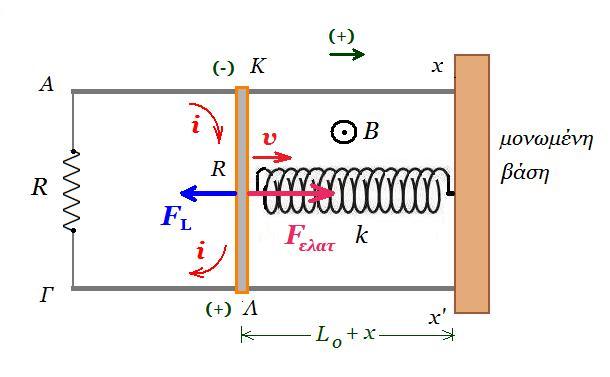
B.    Στην διάταξη του σχήματος, ο αγωγός ΚΛ μήκους l ωμικής αντίστασης R  και μάζας m αποτελεί τμήμα ενός κλειστού κυκλώματος που δημιουργούν οι οριζόντιοι και παράλληλοι αγωγοί-οδηγοί Αx, Γx' και ο αντιστάτης αντίστασης R.
Οι αγωγοί-οδηγοί Αx, Γx'  έχουν αμελητέα αντίσταση και πάνω τους μπορεί να ολισθαίνει ο αγωγός ΚΛ χωρίς τριβές, παραμένοντας διαρκώς κάθετος σε αυτούς. Τα x και x' συνδέονται με ακλόνητη μονωμένη βάση, στο μέσον της οποίας είναι στερεωμένο σε οριζόντιο ιδανικό ελατήριο σταθεράς k του οποίου η άλλη άκρη είναι δεμένη στο μέσον του αγωγού ΚΛ. Η όλη διάταξη βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο του οποίου η ένταση έχει μέτρο Β με τις δυναμικές γραμμές να έχουν φορά από τη σελίδα προς τον αναγνώστη. Εκτρέπουμε τον αγωγό ΚΛ  παράλληλα στον εαυτό του προς τα αριστερά κατά  -Α_ο και τη χρονική στιγμή t=0s τον αφήνουμε ελεύθερο να κινηθεί. Το είδος της κίνησης του αγωγού είναι
α.   φθίνουσα ταλάντωση με την δύναμη αντίστασης να είναι της μορφής F=-bυ.
β.   απλή αρμονική ταλάντωση σταθερού πλάτους Α_ο.
γ.   εξαναγκασμένη ταλάντωση με συχνότητα   f = Φ(k/m) / 2π

ΘΈΜΑ  Γ

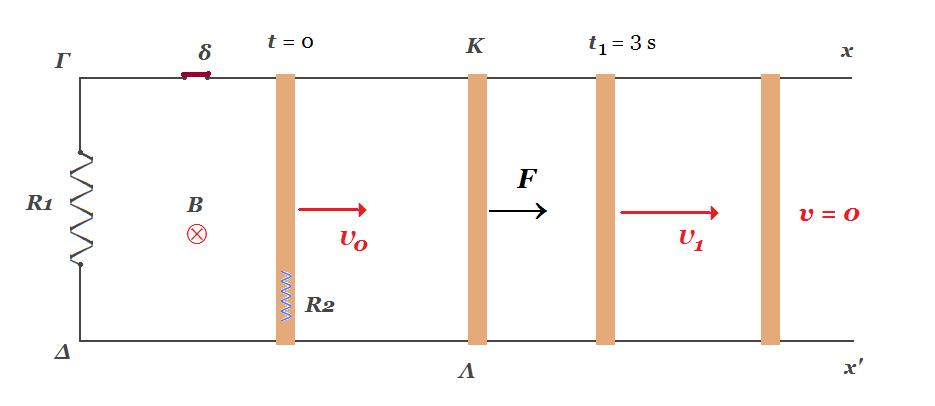
Τα άκρα Γ και Δ  δύο παράλληλων οριζοντίων αγωγών Γx και Δx' αμελητέας ωμικής αντίστασης  συνδέονται με αγωγό αντίστασης R₁ = 0,4 Ω.  Επάνω στυς δύο αγωγούς είναι τοποθετημένος κάθετα προς την διεύθυνσή τους  άλλος ευθύγραμμος αγωγός  ΚΛ  με μήκος  l=1m ,  μάζας m = 0,5 kg ,  ωμικής αντίστασης  R₂ = 0,1 Ω  ο οποίος μπορεί να ολισθαίνει χωρίς τριβές.  Η όλη διάταξη βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο έντασης Β = 1 Τ  με δυναμικές γραμμές κάθετες στο επίπεδο των αγωγών.  Ο αγωγός ΚΛ κινείται με σταθερή ταχύτητα μέτρου  υ₀ = 2 m/s  με τον διακόπτη  δ  ανοικτό.  Τη στιγμή  t = 0  κλείνει ο διακόπτης  δ  χωρίς να δημιουργηθεί σπινθήρας  και ασκείται στον αγωγό ΚΛ  εξωτερική δύναμη F  έτσι ώστε ο αγωγός επιταχύνεται με επιτάχυνση  α = 1 m/s ².  

Γ1.  Γράψτε τη χρονική εξίσωση της δύναμης F.

Γ2.  Βρείτε το επαγωγικό φορτίο που διέρχεται από μια διατομή του αγωγού ΚΛ από τη στιγμή   1 s  έως τη στιγμή  3 s.

Τη στιγμή   t₁ = 3 s  καταργείται  η δύναμη F  και  ο αγωγός ΚΛ επιβραδύνεται μέχρι να μηδενισθεί η ταχύτητά του.  

Γ3.  Υπολογίστε τον ρυθμό μεταβολής της ορμής του ΚΛ τη στιγμή που η ταχύτητά του ισούται με το μισό της μέγιστης τιμής της μετά την κατάργηση της δύναμης F.

Γ4.  Βρείτε τη θερμότητα που εκλύεται από το κύκλωμα κατά τη διάρκεια της επιβραδυνόμενης κίνησης.

Γ1.    E_επαγ = Β υ₀ l  =  1 T . 2 m/s . 1 m = 2 Volt  αρχική επαγωγική τάση στον αγωγό ΚΛ 

  αργότερα ο αγωγός έχει ταχύτητα υ  και το κύκλωμα διαρρέεται με ρεύμα εντάσεως :

   i = E_επαγ / (R₁ + R₂) = Β υ l / (R₁ + R₂)    

  F_L = B i l = Β² l² υ / (R₁ + R₂) = 1 1 υ / 0,5 => F_L = 2υ 

  ΣF = m a  =>  F - F_L = m a  =>   F = 2υ + 0,5 1  => F = 0,5 + 2υ   

ταχύτητα αγωγού : υ = υ₀ + α t  = 2 + t     οπότε    F = 0,5 + 2 ( 2 + t )  => F(t) = 4,5 + 2t     

Γ2.     i = Β l υ / (R₁ + R₂) = 1 1 (2 + t) / 0,5  =  2 (2 + t)  =>   i(t)  =  2t + 4     

 i(1) = 2 + 4 = 6 A     i(3) = 2 3 + 4 = 10 A      q = (3 - 1) [ i(1) + i(3) ] / 2 = 2 (6 + 10) / 2 = 16 C 

Γ3.           υ = υ₀ + α t  = 2 + t = v(t)        v(3) = 2 + 3 = 5 m/s     

ΣF = m a  =>  - F_L = m a  => - Β² l² υ / (R₁ + R₂) = m a  => - 1 1 υ / 0,5 = 0,5 a  => - 4υ = a =>

  => - 4 v = dv/dt  =>  dv/v = - 4 dt  =>   [ ln v ]_5®u  =  - 4 t  =>  lnv - ln5 = - 4t  =>

  =>  ln (v/5) = - 4t  =>  v = 5 e^-4t = v(t)  ταχύτητα         a = dv/dt = - 20 e^-4t = a(t) επιτάχυνση 

  η ταχύτητα μειώνεται εκθετικά με τον χρόνο       το ( - )  στην  α(t) σημαίνει  επιβράδυνση

όταν   υ = υ(3) / 2 = 5/2 = 2,5 m/s     τότε   - υ = 0,25 a  =>  α  =  - 4 2,5 = - 10 m/s²    

ρυθμός μεταβολής ορμής :   Δp / Δt  = ΣF = m a  =  0,5 kg  ( - 10 m/s² )  =  - 5 N  

Γ4.      Q_θερμ = ΔΚ  =  Κ_τελ  -  Κ_αρχ  =  0  -  ½  m υ(3)²  =  ½ 0,5 5²  =  25/4 Joule  

    v = 5 e^-4t = v(t) = dx/dt   =>  dx = 5 e^-4t dt  =>   x(t) = -5/4 ( e^-4t  - 1 )     x(0) = 0  

    τ = 1/4 s ,   5τ = 5/4 s ,   e^{-4 5/4} = e^-5= 0,006738  

        x(5τ)  =  x(5/4)  = - 5/4 ( 0,006738 - 1 ) = 5/4 m

        v(5τ)  =  v(5/4)  =  5  0,006738  = 0    

        a(5τ)  =  a(5/4)  = - 20  0,006738  = 0  

  σε χρόνο  5τ = 5/4 s   ο αγωγός ΚΛ έχει διανύσει απόσταση  5/4 = 1,25 m     και  σταματά 

ΘΕΜΑ  Β 

στη ράβδο ΚΛ ασκείται δύναμη Hooke  F_ελατ = - k x, όπου x<0 η επιμήκυνση του ελατηρίου, με κατεύθυνση οριζόντια προς τα δεξιά     οπότε  μετατοπίζεται κατά  dx σε χρόνο dt  μέσα στο ομογενές μαγνητικό πεδίο  κινούμενη με ταχύτητα  υ = dx / dt  προς τα δεξιά,   τα ηλεκτρόνιά της δέχονται δύναμη Lorenz  και μετακινούνται προς το άκρο Κ  που φορτίζεται αρνητικά,  οπότε το άκρο Λ φορτίζεται θετικά, ή  αλλιώς  η ράβδος κόβει δυναμικές γραμμές  έτσι έχουμε μεταβολή μαγνητικής ροής  σε μια επιφάνεια με εμβαδόν  dA = l Χ dx  έτσι αναπτύσσεται επαγωγική τάση στα άκρα της ράβδου  Ε_επαγ = - dΦ/dt  = - B dA/dt συν0° = - B l dx/dt = - Β l v   συνεπώς το κύκλωμα διαρρέεται με ρεύμα   i  = |Ε_επαγ| / 2R = Β l v  / 2R    οπότε  η ράβδος  δέχεται δύναμη Laplace  μέτρου  F_L = B i l  =  B² l² v / 2R  με κατεύθυνση οριζόντια προς τα αριστερά  

έτσι έχουμε   ΣF  =  F_ελατ  -  F_L  = - k x  - B² l² v / 2R  =  - k x  - b v   όπου   b =  B² l² / 2R  και  x < 0   συνεπώς η ράβδος εκτελεί φθίνουσα ταλάντωση με την δύναμη αντίστασης να είναι της μορφής F=-bυ   με σταθερά απόσβεσης  b =  B² l² / 2R     

   αν οι αντιστάσεις του κυκλώματος είναι μικρές  η σταθερά απόσβεσης είναι μεγάλη  και η περίοδος της ταλάντωσης  αυξάνεται  ενώ το πλάτος της μειώνεται    

   αν οι αντιστάσεις του κυκλώματος είναι πολύ μεγάλες  η σταθερά απόσβεσης  τείνει στο μηδέν  και η ράβδος θα κάνει  περίπου ΑΑΤ  με σταθερά ταλάντωσης  D = k