11.  Ομογενής ράβδος ΟΓ μήκους  l=3m και μάζας Μ=2kg ισορροπεί οριζόντια με τη βοήθεια νήματος που είναι δεμένο στο κέντρο της Κ. Το νήμα σχηματίζει με τη ράβδο γωνία φ=30°  ενώ το άκρο Ο συνδέεται στον τοίχο μέσω άρθρωσης. Στο άκρο Γ είναι δεμένο ελατήριο σταθεράς k=100Ν/m που στο άλλο του άκρο έχει δεθεί σώμα μάζας m=1kg και ισορροπεί.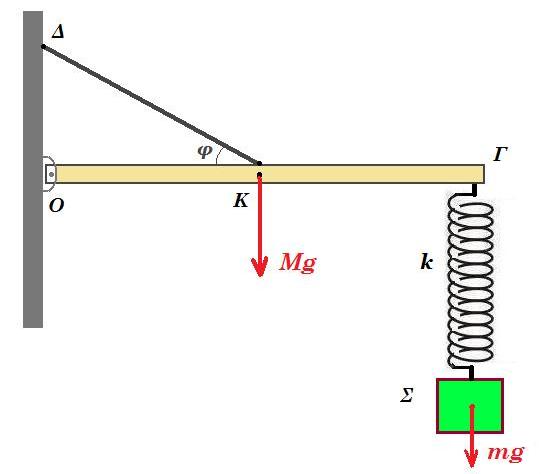 Δίνουμε στο σώμα m στη θέση ισορροπίας της αρχική ταχύτητα υ₀=2m/s με φορά προς τα κάτω οπότε το σύστημα της μάζας και του ελατηρίου αρχίζει να κάνει ΑΑΤ. Το όριο θραύσης του νήματος είναι Τ_θ=120Ν. Να υπολογιστούν:
Α.  Το μέτρο της τάσης του νήματος Τ, όταν το σύστημα μάζα - ελατήριο ισορροπεί.
Β.  Η εξίσωση απομάκρυνσης των ταλαντώσεων της μάζας m, σε σχέση με το χρόνο, αν θεωρηθεί ως t₀=0 η χρονική στιγμή που ξεκίνησε η μάζα m με ταχύτητα υ₀=2m/s και θετική η φορά προς τα κάτω.
Γ.  Η χρονική στιγμή t που θα κοπεί το νήμα.
Δ.  Η ταχύτητα της μάζας m τη στιγμή που κόβεται το νήμα.
Ε.  Ο ρυθμός μεταβολής της στροφορμής όλου του συστήματος τη στιγμή αμέσως μετά το κόψιμο του νήματος. Δίνεται g=10m/s².        

Α.   ισορροπία σώματος :   ΣF = 0  =>  mg  = F_ελατ  =  k x₀  =>  x₀  =  10/100 = 0,1 m  επιμήκυνση ελατηρίου 

ισορροπία ράβδου :  

ροπές ως προς Ο :  Στ_(Ο) = 0  =>   Mg l/2  +  k x₀ l  -  T ημ30° l/2  =  0  => Mg /2  +  k x₀   =  T ½ /2  =>    Τ =  2 Mg  + 4 k x₀  =   2 20 + 4 100 0,1 =>  Τ = 80 Ν  

Β.    τη στιγμή t = 0  το ελατήριο είναι επιμηκυμένο κατά 0,1 m,  το σώμα έχει ταχύτητα υ₀=2m/s  με φορά προς τα κάτω ( θετική φορά )  και ισορροπεί

διατήρηση ενάργειας για την ταλάντωση :   ½ m υ²  =  ½  k Α²  =>   1 2²  =  100 Α²   =>  Α = 0,2 m    πλάτος ταλάντωσης σώματος

 ω²  =  k / m  = 100 / 1  =>  ω = 10 rad/s         T = 2π/ω = 2π/10 = π/5 s

  x(t) = 0,2 ημ10t       υ(t) = 2 συν10t         α(t) = - 20 ημ10t

  ΣF(t) = - 20 ημ10t          

ΣF(t) = - 20 ημ10t  =>  mg  +  F_ελατ = - 20 ημ10t      =>   F_ελατ(t) = - 10 - 20 ημ10t     

t = 0     F_ελατ(0) = - 10 N     δύναμη ελατηρίου  με κατεύθυνση κατακόρυφη προς τα πάνω

t = T/4 = π/20 s     F_ελατ(π/20) = - 10 - 20 ημ10(π/20) = - 10 - 20 = - 30 N  μέγιστη δύναμη ελατηρίου  με κατεύθυνση κατακόρυφη προς τα πάνω,    το ελατήριο είναι επιμηκυμένο κατά  0,3 m 

t = 3T/4 = 3π/20 s     F_ελατ(3π/20) = - 10 - 20 ημ10(3π/20) = - 10 + 20 = + 10 N  μέγιστη δύναμη ελατηρίου  με κατεύθυνση κατακόρυφη προς τα κάτω,     το ελατήριο είναι συσπειρωμένο κατά  0,1 m  

Γ.  Δ.          F_Γ  =  - F_ελατ(t) = 10 + 20 ημ10t     

ροπές ως προς Ο :  Στ_(Ο) = 0  =>   Mg l/2  + F_Γ  l  + T_y  l/2  =  0  =>

=>    T_y   =  - Mg   - 2 F_Γ    =   - 20   - 2 ( 10 + 20 ημ10t ) =  - 40 - 40 ημ10t   =  T_y(t)   

t = 0       T_y(0)  = - 40 N   κατακόρυφη προς τα πάνω   

το νήμα κόβεται όταν η τάση  |Τ| = 120 Ν  =>   |T_y|   = |Τ| ημ30° =  120  ½  =  60 Ν  

T_y   =  - 60 Ν  =>   - 40 - 40 ημ10t  =  - 60  =>  ημ10t = + ½  =  ημ(π/6)  =>   t = π/60 s   

δηλαδή καθώς ταλαντώνεται το σώμα  τη στιγμή  t = π/60 s  καθώς κινείται προς τα κάτω (θετική φορά) κόβεται το νήμα  

x(π/60) = 0,2 ημ10(π/60) =  0,1 m           υ(π/60) = 2 συν10(π/60) = 2 Φ3/2 =  Φ3 m/s  προς τα κάτω

F_ελατ(π/60) = - 10 - 20 ημ10(π/60) = - 10 - 20 . ½ = - 20 Ν  το ελατήριο είναι επιμηκυμένο κατά 0,2 m   

E.   τη στιγμή που κόβεται το νήμα  η τάση  νήματος είναι μηδέν,  οι δυνάμεις στη ράβδο και στο σώμα λόγω του ελατηρίου είναι εσωτερικές του συστήματος,  άρα οι εξωτερικές δυνάμεις  Mg  και  mg  κάνουν ροπή

 dL/dt = Στ_(Ο) =  Mg l/2  +  mg l  =  20  3/2  +  10  3  =  60 kg m²/s²  =  60 N m