ποια είναι η αλγεβρική τιμή της ΗΕΔ επαγωγής που αναπτύσσεται στο κύκλωμα σε συνάρτηση με το χρόνο;
Εφαρμογή για Β0 = 1Τ, ω=10rad/s, υ = 2m/s, l =1m, R = 0,5 Ohm
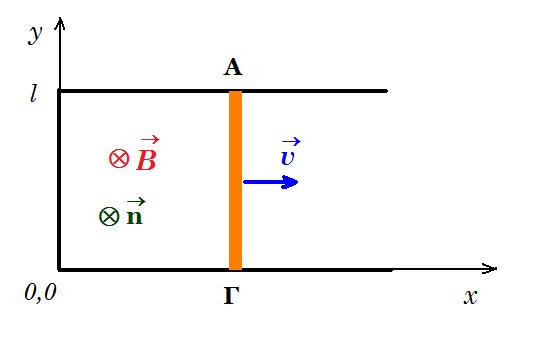
Ένας ευθύγραμμος αγωγός ΑΓ, κινείται χωρίς τριβές πάνω σε οριζόντιο επίπεδο, με τα άκρα του πάνω σε δύο παράλληλους αγωγούς, που απέχουν απόσταση l και έχουν τα αριστερά τους άκρα βραχυκυκλωμένα, όπως στο σχήμα. Ο αγωγός είναι συνεχώς παράλληλος με τον άξονα Oy, ενώ τη χρονική στιγμή t = 0, βρίσκεται στη θέση x = 0. Στο χώρο υπάρχει εκτεταμένο κατακόρυφο ομογενές μαγνητικό πεδίο αρμονικής αλγεβρικής τιμής B = B0 ημ(ω t). Ο αγωγός ΑΓ έχει αντίσταση R, ενώ οι άλλοι δύο αγωγοί έχουν αμελητέα αντίσταση. Αν η ταχύτητα του αγωγού έχει σταθερό μέτρο υ και είναι κάθετη στον αγωγό και στις μαγνητικές δυναμικές γραμμές
ποια είναι η αλγεβρική τιμή της ΗΕΔ επαγωγής που αναπτύσσεται στο κύκλωμα σε συνάρτηση με το χρόνο;
Εφαρμογή για Β0 = 1Τ, ω=10rad/s, υ = 2m/s, l =1m, R = 0,5 Ohm
επαγωγική τάση εμφανίζεται λόγω μεταβολής του μέτρου της έντασης Β και λόγω της κίνησης του αγωγού μέσα στο μεταβαλλόμενο μαγνητικό πεδίο έστω μετακινείται κατά x σε χρόνο t
Φ = Β Α = B0 ημ(ω t) l x = B0 ημ(ω t) l υ t
Εεπαγ = dΦ / dt = d/dt { B0 ημ(ω t) l υ t } = B0 ω συν(ω t) l υ t + B0 ημ(ω t) l υ
Εεπαγ = Β l dx/dt + dB/dt l x = B0 ημ(ω t) υ l + B0 ω συν(ω t) l υ t =
= 1 ημ(10 t) 2 1 + 1 10 συν(10 t) 1 2 t = 2 ημ(10 t) + 20 t συν(10 t)
iεπαγ = Εεπαγ / R = [ 2 ημ(10 t) + 20 t συν(10 t) ] / 0,5 = 4 ημ(10 t) + 40 t συν(10 t)
FL = B iεπαγ l = B0 ημ(ω t) [ 4 ημ(10 t) + 40 t συν(10 t) ] 1 =
= 1 ημ(10 t) [ 4 ημ(10 t) + 40 t συν(10 t) ] 1 = 4 ημ(10 t) [ ημ(10 t) + 10 t συν(10 t) ]
= 4 ημ2 (10 t) + 40 t ημ(10 t) συν(10 t) =
= 2 { 1 - συν(20 t) } + 20 t ημ(20 t) =>
FL (t) = 2 - 2 συν(20 t) + 20 t ημ(20 t)
συν2α = συν2α - ημ2α = 1 - ημ2α - ημ2α = 1 - 2 ημ2α => 2 ημ2α = 1 - συν2α
ημ2α = 2 ημα συνα