ΘΕΜΑ Γ
Οι μεγάλου μήκους, κατακόρυφοι, μεταλλικοί αγωγοί Α x και Γy απέχουν μεταξύ τους σταθερή απόσταση ℓ = 1 m και έχουν αμελητέα ωμική αντίσταση.
Στα άκρα Α, Γ συνδέεται πηγή ηλεκτρεγερτικής δύναμης Ε = 9 V και εσωτερικής αντίστασης r = 1 Ω. Αγωγός ΚΛ μήκους ℓ = 1 m, μάζας m = 0,3 kg και ωμικής αντίστασης RΚΛ = 2 Ω έχει τα άκρα του Κ , Λ πάνω στους κατακόρυφους αγωγούς Αx και Γy, είναι κάθετος σε αυτούς και είναι δυνατόν να ολισθαίνει κατά μήκος των αγωγών χωρίς τριβές. Η όλη διάταξη βρίσκεται σε περιοχή που υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης B , του οποίου οι δυναμικές γραμμές είναι κάθετες στο επίπεδο του σχήματος.
Αρχικά ο διακόπτης δ1 είναι κλειστός, ο διακόπτης δ2 είναι ανοικτός και ο αγωγός ΚΛ είναι ακίνητος στη θέση 1.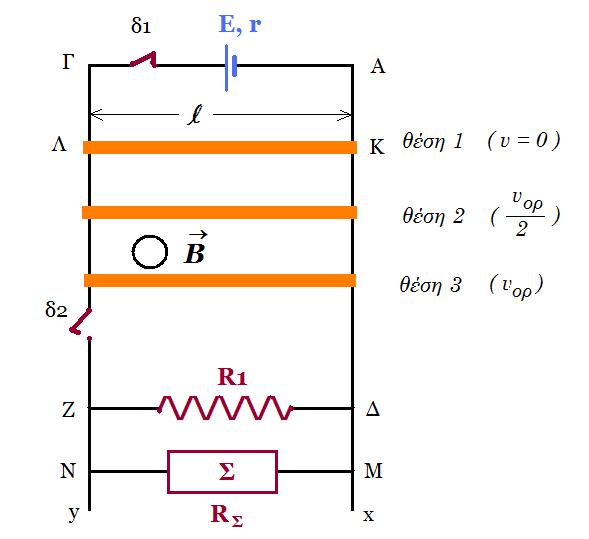
Γ1.   Να υπολογίσετε το μέτρο Β της έντασης του μαγνητικού πεδίου  και να προσδιορίσετε την κατεύθυνσή της. Στο κάτω μέρος της διάταξης, μεταξύ των σημείων Ζ και Δ, είναι συνδεδεμένος αντιστάτης με ωμική αντίσταση R1 = 3 Ω και στα σημεία Μ, Ν  είναι συνδεδεμένη θερμική συσκευή Σ ωμικής αντίστασης RΣ , η οποία όταν στα άκρα της Μ, Ν έχει τάση ίση με 6 V λειτουργεί κανονικά αποδίδοντας θερμική ισχύ 6 W.
Ανοίγουμε το ν διακόπτη δ1 , κλείνοντας ταυτόχρονα τον διακόπτη δ2 και ο αγωγός ΚΛ αρχίζει να κατέρχεται παραμένοντας συνεχώς οριζόντιος χωρίς τα άκρα του Κ, Λ να χάνουν την επαφή με τους αγωγούς Αx και Γy.
Γ2.   Έστω ότι ο αγωγός ΚΛ έχει αποκτήσει οριακή ταχύτητα  uορ  στη θέση 3.
Να δικαιολογήσετε το είδος της κίνησης που εκτελεί ο αγωγός ΚΛ από τη θέση 1 έως τη θέση 3 και να υπολογίσετε τη σταθερή οριακή ταχύτητα uορ.
Γ3.   Να υπολογίσετε τον ρυθμό μεταβολής της ορμής του αγωγού στη θέση 2, στην οποία η ταχύτητά του είναι ίση με  uορ/2 .
Γ4.   Όταν ο αγωγός έχει αποκτήσει την οριακή του ταχύτητα, να εξετάσετε αν η θερμική συσκευή Σ λειτουργεί κανονικά.

E = i (R_ΚΛ +  r)  =>  9 = i ( 2 + 1 )  =>   i = 3 Α 

ΣF = 0  =>  F_L = m g   =>   B i l  =  m g  =>   B  3  1  =  0,3  10  =>   B = 1 T   οριζόντιο προς τα μέσα 

θερμική συσκευή :   P = V I  =>  6W = 6V  I  =>  I = 1A               R_Σ  =  V / I  =  6 Ohm

η συσκευή και η αντίσταση R₁ συνδέονται παράλληλα και η ισοδύναμη αντίσταση είναι 2 Ω

η ΚΛ καθώς κινείται προς τα κάτω μέσα στο μαγνητικό πεδίο  τα ηλεκτρόνιά της δέχονται δύναμη Lorenz  και  οδεύουν προς το άκρο Λ  που φορτίζεται αρνητικά  ενώ το άκρο Κ  θετικά  έτσι  στα άκρα της αναπτύσσεται επαγωγική τάση  Ε_επαγ = Β υ l = 1 υ 1 = υ    οπότε το κύκλωμα διαρρέεται με επαγωγικό ρεύμα 

    i_επαγ =  Ε_επαγ / ( R_ΚΛ + R_Σ,1 ) =  Β υ l / ( R_ΚΛ + R_Σ,1 ) =  1 υ  1 / (2+2)  =>   i_επαγ =  υ/4 

η ΚΛ  δέχεται δύναμη Laplace  αντίρροπη του βάρους :   F_L =  B i l  =  1  υ/4  1  =  υ/4   

η τάση  στα άκρα της ΚΛ είναι :

   V_ΚΛ  =  Ε_επαγ  -   i_επαγ R_ΚΛ    =   υ  -  υ/4  2   =  υ  -  υ/2  =  υ/2  

η ισχύς που καταναλώνεται πάνω στην αντίσταση της ΚΛ  είναι :

    P_ΚΛ  =  i_επαγ²  R_ΚΛ    =  ( υ/4 )²  2  =  υ² / 8   =  υ/2   υ/4   = V_ΚΛ  i_επαγ   

πτώση της ράβδου ΚΛ :   ΣF = m a  =>  m g  -  F_L  =  m a  =>   m g  -  B i l  =  m a

    =>   0,3  10  -   1  υ/4   1  =  0,3 a  =>   3  - υ/4  =  0,3 a  =>   12  - υ  =  1,2  dυ/dt    =>   

    =>   dυ / (υ - 12)  =  - dt/1,2   =>    ln (υ - 12)  -  ln (- 12)  =  - t/1,2  =>

    =>   ln { (υ - 12)/(-12) }  = - t/1,2   =>   (υ - 12)  =  - 12 e^-t/1,2  =>    υ(t)  =  12  - 12 e^-t/1,2  

υ(0)  =  12  - 12 e⁰  =  12 - 12 = 0                 υ(¥)  =  12  - 12 e^-¥   =  12 m/s   οριακή ταχύτητα

υ_ορ = 12 m/s      όταν  υ = υ_ορ /2 = 6 m/s     τότε  από την σχέση :  3  - υ/4  =  0,3 a  => 3  - 6/4  =  0,3 a  =>  1,5 / 0,3  =  a  =>   a  =  5 m/s²   επιτάχυνση ράβδου ΚΛ  

 τότε ΣF = m a  =  0,3  5  = 1,5 Ν = dp/dt   ο ρυθμός μεταβολής της ορμής εκείνη την στιγμή

     υ(t)  =  12  - 12 e^-t/1,2  =>  6  =  12  - 12 e^-t/1,2  =>   12 e^-t/1,2  =  12  - 6  =  6  =>   e^-t/1,2  = ½  =>   e^t/1,2  =  2   =>   t/1,2  =  ln2  =>  t  =  1,2 ln2 sec  »   1,2  0,7 s  =  0,84 s

  υ(t)  =  12 ( 1 - e^-t/1,2 )             a(t) = dυ/dt  = - 12/(-1,2) e^-t/1,2  =  10 e^-t/1,2     

  i(t) = υ(t) / 4 =  ( 12 - 12 e^-t/1,2 ) / 4  =   3 ( 1 - e^-t/1,2 )      

  V_ΚΛ(t)  =  υ(t) / 2 =  ( 12 - 12 e^-t/1,2 ) / 2  =  6 ( 1 - e^-t/1,2 )    

  Ρ_ΚΛ(t)  =  υ(t)² / 8 =  ( 12 - 12 e^-t/1,2 )² / 8  =  6 ( 1 - e^-t/1,2 )  3 ( 1 - e^-t/1,2 )  =  18 ( 1 - e^-t/1,2 )²      

  F_L(t)  =  B  i(t)  l  =  3 - 3 e^-t/1,2    

F_L(0)  =  3  - 3 e⁰  =  3 - 3 = 0                 F_L(¥)  =  3  -  3 e^-¥  =  3 N  =  0,3 kg  10 m/s²  =  m g  

όταν αποκτήσει η ΚΛ την οριακή της ταχύτητα 12 m/s το επαγωγικό ρεύμα έχει τιμή Ι = 3Α

η τάση στα άκρα της είναι  V_ΚΛ  =  Ε_επαγ  -  Ι R_ΚΛ  = Β υ l  -  Ι R_ΚΛ  =  1  12  1  -  3  2  = 6 Volt  

στα άκρα της συσκευής επικρατεί τάση   V_Σ  =  Ι R_Σ,1  =  3 Α  2 Ω =  6 Volt  

                  συνεπώς η θερμική συσκευή λειτουργεί κανονικά 

  υ(t)  =  12  - 12 e^-t/1,2    =  dx / dt     =>     dx  =  12 dt  -  12 e^-t/1,2 dt         

    x(t)  =  12 t   -  12 (-1,2)  ( e^-t/1,2 -  e⁰ )    =>     x(t)  =  12 t   +  14,4 ( e^-t/1,2 - 1 )   διανυόμενο διάστημα από τον αγωγό ΚΛ 

 υ(t)  =  12 - 12 e^-t/1,2      a(t)  =  10 e^-t/1,2      x(t)  =  12 t  +  14,4 ( e^-t/1,2 - 1 ) 

     ταχύτητα                                επιτάχυνση                                  διάστημα

την στιγμή  t = 1,2 ln2 s    η ΚΛ  έχει ταχύτητα   υ = υ_ορ /2 = 6 m/s ,  

 επιτάχυνση  a(1,2 ln2) = 10 e^{-1,2 ln2/1,2}   =  10 / 2 =  5 m/s²         

  και έχει διανύσει διάστημα   x(1,2 ln2)  =  12 1,2 ln2  +  14,4 ( e^{-1,2 ln2/1,2} - 1 )   = 14,4 ln2  +  14,4 ( e^{- ln2} - 1 )   =   14,4 ln2  +  14,4 ( ½ - 1 )   = 14,4 ln2  -  7,2 μέτρα  =  2,78 μέτρα

ο αγωγός ΚΛ  αποκτά την οριακή ταχύτητα μετά από χρόνο  t = 5 1,2 s = 6 s  

τότε    υ(6)  =  12  - 12 e^-6/1,2   =  12  -  12 e^-5  =  12  -  12  0,006738  =  12  - 0,08  =  11,92 m/s   »  12 m/s

η επιτάχυνση της είναι   a(6) = 10 e^-6/1,2   =  10 e^-5   = 10  0,006738 m/s²  »  0  

έχει διανύσει μέχρι τότε διάστημα   x(6)  =  12  6  +  14,4 ( e^-6/1,2 - 1 )  =  72  +  14,4 ( 0,006738 - 1 )  =  72  +  14,4  ( - 1 ) =  72  -  14,4  =  57,6  μέτρα