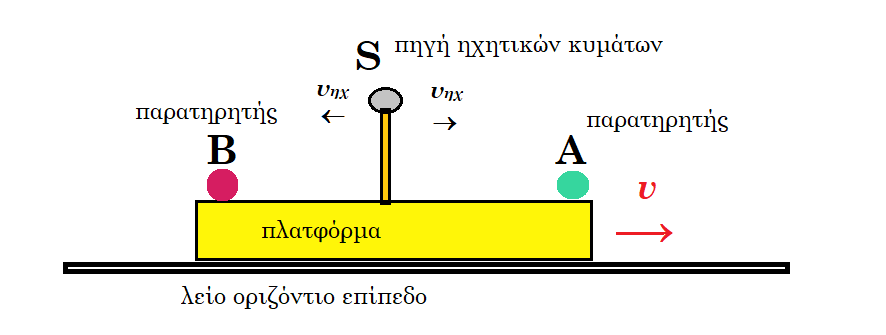
Β1.  Τρένο κινείται ευθύγραμμα σε οριζόντιο επίπεδο με σταθερή ταχύτητα μέτρου υ_ηχ/10, όπου υ_ηχ είναι η ταχύτητα διάδοσης του ήχου στον αέρα. 
Το τρένο κατευθύνεται προς τούνελ που βρίσκεται σε κατακόρυφο βράχο.
Ο ήχος που εκπέμπεται από τη σειρήνα του τρένου ανακλάται στον κατακόρυφο βράχο.  Ακίνητος παρατηρητής  βρίσκεται πάνω στις γραμμές και πίσω από το τρένο ακούει δύο ήχους. Έναν ήχο απευθείας από τη σειρήνα του τρένου, με συχνότητα f₁, και έναν ήχο από την ανάκλαση στον κατακόρυφο βράχο, με συχνότητα f₂. Ο λόγος των δύο συχνοτήτων  f₁/f₂  είναι ίσος με:

i.  11/9            ii.  10/11             iii.  9/11

ο παρατηρητής είναι ακίνητος και η πηγή απομακρύνεται :

         f₁ = f_s  υ_ηχ / ( υ_ηχ + υ_ηχ/10 ) =  f_s  υ_ηχ / ( 11/10 υ_ηχ )  =  10/11  f_s   

ο βράχος είναι ακίνητος και η πηγή πλησιάζει   ο ακίνητος παρατηρητής ακούει τη συχνότητα του ήχου που ανακλάται στον ακίνητο βράχο :

         f₂ = f_s  υ_ηχ / ( υ_ηχ - υ_ηχ/10 ) =  f_s  υ_ηχ / ( 9/10 υ_ηχ )  =  10/9  f_s           f₁ / f₂  =  9/11  

διακρότημα 2016

Β2.    Ακίνητη πηγή S  ηχητικών κυμάτων μάζας  m  εκπέμπει ήχο συχνότητας  f_S.   Το μήκος κύματος είναι λ_S.  Ανιχνευτής ηχητικών κυμάτων μάζας  2m  κινείται προς την πηγή με ταχύτητα μέτρου  υ_ηχ / 4,  όπου  υ_ηχ  είναι η ταχύτητα διάδοσης του ήχου στον αέρα.  Ο ανιχνευτής και η πηγή συγκρούονται μετωπικά και ελαστικά.  

Α.   Η μεταβολή του μήκους κύματος που καταγράφει ο ανιχνευτής  πριν  και  μετά την κρούση είναι :  

    α)    υ_ηχ / 2f_S,        β)    υ_ηχ / f_S,         γ)    υ_ηχ / 3f_S,

Β.   Η μεταβολή της συχνότητας του ήχου που καταγράφει ο ανιχνευτής πριν  και  μετά την κρούση είναι :  

    α)    Δf_Α  =  - 7/16 f_S,        β)    Δf_Α  =  - 9/16 f_S,         γ)    Δf_Α  =  - 7/4 f_S,

ο ανιχνευτής πλησιάζει την ακίνητη πηγή   ( η ταχύτητα του ήχου ως προς τον ανιχνευτή είναι υ_ηχ + υ_ηχ/4 )               λ₁ =  λ_s  =  υ_ηχ / f_s      

       f₁ = ( υ_ηχ + υ_ηχ/4 ) / λ₁   =   f_s  ( υ_ηχ + υ_ηχ/4 ) / υ_ηχ   =   5/4 f_s   

κρούση μετωπική - ελαστική :  

  υ₁'  =  υ₁  ( 2m - m ) / ( 2m + m ) =  1/3  υ₁   =  1/3  υ_ηχ/4  =  υ_ηχ/12

  υ_s '  =  2 2m υ₁  / ( 2m + m ) =  4/3  υ₁  =  4/3  υ_ηχ/4  =  υ_ηχ/3

μετά την κρούση   η πηγή απομακρύνεται  ενώ  ο ανιχνευτής πλησιάζει ( η ταχύτητα του ήχου ως προς τον ανιχνευτή είναι υ_ηχ + υ_ηχ/12  )  

   λ₂ =  λ_s  + υ_ηχ/3  Τ  =  υ_ηχ / f_s  +  υ_ηχ / 3f_s   =  ( υ_ηχ  +  υ_ηχ/3 ) /  f_s   

  f₂ = ( υ_ηχ + υ_ηχ/12 ) / λ₂  =   f_s  ( υ_ηχ + υ_ηχ/12 ) / ( υ_ηχ + υ_ηχ/3 )  =  (13/12) / (4/3)  f_s  =  13/16  f_s 

μεταβολή μήκους κύματος :   λ₂  -  λ₁  =    υ_ηχ / f_s  +  υ_ηχ / 3f_s  -  υ_ηχ / f_s  =  υ_ηχ / 3f_s 

μεταβολή συχνότητας :    f₂  -   f₁ =  13/16  f_s  -   5/4 f_s   =  - 7/16  f_s   

Ο Ε Φ Ε   2017

Β2.   Παρατηρητής Α κινείται με σταθερή ταχύτητα μέτρου  υ_Α  μεταξύ δύο

 ακίνητων και όμοιων πηγών S₁  και S₂,  από την (1)  προς την (2),  που εκπέμπουν ήχο της ίδιας συχνότητας  f_S. Ο παρατηρητής Α λαμβάνει δύο ηχητικά κύματα, η σύνθεση των οποίων δημιουργεί διακρότημα.  Το πλάτος του ήχου που αντιλαμβάνεται ο παρατηρητής Α μεγιστοποιείται με συχνότητα  f_S / 100.   Θεωρούμε ότι τα πλάτη των ήχων των δύο πηγών δεν μεταβάλλονται με την απόσταση.  Αν το μέτρο της ταχύτητας του ήχου στον ακίνητο αέρα είναι ίσο με υ_ηχ  τότε ισχύει : 

   α)   υ_Α  =  υ_ηχ / 50             β)   υ_Α  =  υ_ηχ / 100             γ)   υ_Α  =  υ_ηχ / 200        

  f₁  =  f_s  ( υ_ηχ - υ_Α ) / υ_ηχ           f₂  =  f_s  ( υ_ηχ + υ_Α ) / υ_ηχ    

    f₂  -  f₁  =     2 f_s  υ_Α  / υ_ηχ                    1 / Τ =  1 /  ( f₂  -  f₁ )   =>  f_s / 100  =  υ_ηχ /  2 f_s  υ_Α    =>   υ_Α  =  υ_ηχ / 200 

Β3. Αυτοκίνητο της τροχαίας κινείται σε ευθύ δρόμο με σταθερή ταχύτητα υ₁=υ/10 και έχει
ενεργοποιημένη τη σειρήνα του, η οποία παράγει ήχο συχνότητας fs  μήκους κύματος λ.
Μοτοσικλετιστής που προπορεύεται  κινείται με ταχύτητα μέτρου υ₂= υ/20  προς την ίδια κατεύθυνση, ακούει ήχο

Ι. με συχνότητα:           α)  fA=19fs/18          β)  fA=20fs/18              γ)  fA=21fs/19

ΙΙ. με μήκος κύματος :    α)  λ               β)  0,9 λ                   γ)  1,1 λ

  όπου   υ  η ταχύτητα διάδοσης του ήχου στον αέρα

το περιπολικό πλησιάζει τον μοτοσικλετιστή  με ταχύτητα  υ₁  οπότε  αυτός  αντιλαμβάνεται μήκος κύματος  λ_Α  =  λ - υ₁ Τ =  λ - υ/10 1/f_s  =  λ - λ/10  =  0,9 λ        όπου   υ = λ f_s 

ο μοτοσικλετιστής προπορεύεται   απομακρύνεται με ταχύτητα  υ₂  οπότε η ταχύτητα του ήχου ως προς αυτόν είναι  υ -  υ₂  =  υ -  υ/20  =  19υ/20 

η συχνότητα  που αντιλαμβάνεται ο μοτοσικλετιστής είναι :

   f_A  =  ( υ -  υ₂ ) / λ_Α  =  19v/20 0,9 λ  =  19/18 υ λ  =  19 f_s / 18

δηλαδή :  f_Α = f_s  ( υ_ηχ - υ_ηχ /20) / ( υ_ηχ - υ_ηχ /10 ) =  f_s  19/20 υ_ηχ  / ( 9/10 υ_ηχ )  =  19/18  f_s   

Β4.  Ηχητική πηγή κινείται με σταθερή ταχύτητα υ_s προς ακίνητο παρατηρητή. Τα μήκη κύ ματος που εκπέμπει η πηγή προς την κατεύθυνση του παρατηρητή, πριν και μετά τη διέλευση της από αυτόν, διαφέρουν μεταξύ τους κατά λ/10 , όπου λ το μήκος κύματος που εκπέμπει η πηγή όταν είναι ακίνητη.  Αν υ η ταχύτητα διάδοσης του ήχου στον αέρα, ο λόγος  υ_s/υ είναι:        

     (α)   1/5             (β)    1/10           (γ)  1/20

η πηγή πλησιάζει τον ακίνητο παρατηρητή Α  ο οποίος αντιλαμβάνεται μήκος κύματος  λ₁ =  λ - υ_s Τ  η πηγή  προσπερνά  και   απομακρύνεται από τον ακίνητο παρατηρητή Α που αντιλαμβάνεται μήκος κύματος  λ₂ =  λ  + υ_s Τ                                        

  ισχύει η σχέση :  λ₂  -  λ₁  =  λ/10  =>   λ  + υ_s Τ  -  ( λ  - υ_s Τ )  =  λ/10  =>  2 υ_s Τ  = λ/10  => 

       =>   υ_s  = λ/20Τ  =  υ/20  =>   υ_s / υ  = 1/20 

Β7.   Περιπολικό  πλησιάζει με ταχύτητα υ_s  προς ένα κατακόρυφο τοίχο και εκπέμπει με τη
σειρήνα του ήχο συχνότητας f_s , ο οποίος διαδίδεται με ταχύτητα, υ. Παρατηρητής Α που στέκεται ακίνητος πίσω από το περιπολικό μπορεί να αντιλαμβάνεται ήχους απευθείας και από ανάκλαση στον τοίχο.  Αν η ταχύτητα του αυτοκινήτου είναι πολύ μικρότερη της ταχύτητας του ήχου,
ο παρατηρητής, Α ακούει διακροτήματα με συχνότητα
α)   f_δ = 2υυs / ( υ² - υ_s² ) f_s                  β)   f_δ = 2υυs / ( υ² + υ_s² ) f_s                     γ)   f_δ = f_s    

 το περιπολικό απομακρύνεται από τον παρατηρητή    f₁ = f_s  υ / ( υ + υ_s )              υ = λ f_s 

         λ₁ = λ + υ_s Τ =  υ / f_s  + υ_s / f_s  =  ( υ + υ_s ) / f_s  =  ( υ + υ_s ) λ/υ  =  λ ( υ + υ_s )/υ 

 το περιπολικό πλησιάζει τον ακίνητο τοίχο   f₂ = f_s  υ / ( υ - υ_s )   ο ήχος ανακλάται και φθάνει στον ακίνητο παρατηρητή Α 

      λ₂ = λ - υ_s Τ = υ / f_s  -  υ_s / f_s  =  ( υ - υ_s ) f_s  =  ( υ - υ_s ) λ/υ  =  λ ( υ - υ_s )/υ 

 διακρότημα  f_δ =  f₂  - f₁  =  f_s  υ / ( υ - υ_s )  -  f_s  υ / ( υ + υ_s )  =   f_s  υ [ 1/( υ - υ_s ) - 1/( υ + υ_s ) ]  =  

       =   f_s  υ   ( υ + υ_s - υ + υ_s ) / ( υ - υ_s )( υ + υ_s )   =   f_s  2 υ υ_s / ( υ² - υ_s² )  

η διαφορά των μηκών κύματος που αντιλαμβάνεται ο παρατηρητής είναι :  Δλ =  λ₁ - λ₂  = 2λ υ_s /υ    

Β8.  Περιπολικό κινείται προς τα δεξιά πλησιάζοντας κατακόρυφο τοίχο με ταχύτητα υ_s  και ταυτόχρονα εκπέμπει ήχο μήκους κύματος λ.  Ο παρατηρητής Α βρίσκεται πίσω από το περιπολικό και κινείται προς αντίθετη κατεύθυνση με υ_Α < υ_s.   Ο παρατηρητής αντιλαμβάνεται δύο ήχους.  Ο ένας έχει μήκος κύματος λ₁ και  έρχεται απευθείας από το περιπολικό  και  ο άλλος μήκος κύματος λ₂  και φτάνει σ’ αυτόν από ανάκλαση.   Για τα μήκη κύματος ισχύει:
α. λ1=λ2=λ              β. λ1+λ2=λ                γ. λ1-λ2=2λ                 δ. λ1+λ2=2λ

το περιπολικό απομακρύνεται από τον παρατηρητή Α     f₁ = f_s  ( υ - υ_Α ) / ( υ + υ_s )       υ = λ f_s 

         λ₁ = λ + υ_s Τ =  λ  + υ_s / f_s  =  ( υ + υ_s ) / f_s  =  ( υ + υ_s ) λ/υ  =  λ ( υ + υ_s )/υ 

 το περιπολικό πλησιάζει τον ακίνητο τοίχο   f₂ = f_s  υ / ( υ - υ_s )   ο ήχος ανακλάται και φθάνει στον  παρατηρητή Α που κινείται αντίθετα ως προς το περιπολικό   ( είναι σαν να πλησιάζει η πηγή τον παρατηρητή )

      λ₂ = λ - υ_s Τ = υ / f_s  -  υ_s / f_s  =  ( υ - υ_s ) f_s  =  ( υ - υ_s ) λ/υ  =  λ ( υ - υ_s )/υ 

              λ₁  +  λ₂  =   λ ( υ + υ_s )/υ  +  λ ( υ - υ_s )/υ   =  2 λ 

              λ₁  -  λ₂  =   λ ( υ + υ_s )/υ  -  λ ( υ - υ_s )/υ   =  2 λ υ_s /υ               

Β9.   Σώμα S μάζας m διαθέτει πηγή ήχων και εκπέμπει ήχο συχνότητας  f_s  και μήκους κύματος λ. Το σώμα κινείται με σταθερή ταχύτητα μέτρου υ₁=υ/5, όπου υ η ταχύτητα του ήχου, και πλησιάζει προς άλλο ακίνητο σώμα, A, μάζας 2m που διαθέτει ανιχνευτή ήχων.  Το S συγκρούεται κεντρικά ελαστικά με το A.  Μετά την κρούση τα σώματα κινούνται με σταθερές ταχύτητες.
Α.  Αν f₁  είναι η συχνότητα που καταγράφει ο ανιχνευτής πριν την κρούση και  f₂  η συχνότητα
που καταγράφει μετά την κρούση τότε ο λόγος  f₁/f₂ είναι:

            α)   13/20               β)   20/13                γ)   25/13

Β.  Μετά την κρούση ο Α καταγράφει μήκος κύματος  λ_Α   ίσο με :   

              α)  λ           β)  16λ/15       γ)  15λ/16          δ)  17λ/16

κεντρική εαστική κρούση :    v₁'  =  v₁  (m - 2m) / (m + 2m)  =  - v₁ /3  =  - υ/15

                                              v₂'  =  2 v₁ m / (m + 2m)  =  2v₁ /3   =  2υ/15   

πριν την κρούση η πηγή πλησιάζει τον Α με ταχύτητα υ₁  και  ο Α  αντιλαμβάνεται μήκος κύματος :  λ₁  =  λ  -  υ₁ Τ  =   λ  -  υ/5 Τ  =  λ  -  λ/5  =>    λ₁  =  4λ/5         

ο Α αντιλαμβάνεται συχνότητα :    f₁  =  f_s  v / (v - v₁)  =  f_s  v / (v - v/5)  =   f_s 5/4

μετά την κρούση η πηγή απομακρύνεται από τον παρατηρητή Α  με ταχύτητα υ₁'  και  ο Α  αντιλαμβάνεται μήκος κύματος :  λ₂  =  λ  +  |υ₁'| Τ  =   λ  +  υ/15 Τ  =  λ  +  λ/15  =>    λ₂  =  16λ/15             

ο Α αντιλαμβάνεται συχνότητα :    f₂  =  f_s  (v- v₂') / (v + |v₁'|)  =  f_s  (v - 2υ/15) / (v + v/15)  =   f_s  13/16

      τελικά       f₁ / f₂  =  20/13           

πριν την κρούση :      S ®^υ1    Α                       μετά την κρούση :     ^υ1'¬   S         Α  ®^υ2'  

Β10.   Η πλατφόρμα κινείται ευθύγραμμα με σταθερή ταχύτητα  υ = 34 m/s.  Η ηχητική πηγή που είναι πάνω της εκπέμπει ήχο με συχνότητα f_s = 680 Hz.  Οι δύο παρατηρητές Α και Β βρίσκονται
πάνω στη πλατφόρμα ακίνητοι ως προς αυτή.  Ο ήχος έχει ταχύτητα  υ_ηχ = 340 m/s.  Τα μήκη κύματος μετράνε για τον ήχο είναι:
    α)   λ_Α = λ_Β = 0.5m            β)   λ_Α = 0,40 m ,   λ_Β = 0,60 m               γ)   λ_Α = 0,45 m ,   λ_Β = 0,55 m

  η πηγή  και οι παρατηρητές  Α,  Β  είναι  ακίνητοι ως προς την πλατφόρμα,   η οποία όμως κινείται μα σταθερή ταχύτητα  υ  ως προς τον ακίνητο αέρα   έτσι  η ταχύτητα του αέρα ως προς τον παρατηρητή Α  είναι  υ_ηχ - υ  ( υ_ηχ , υ  ομόρροπα διανύσματα )    και   για τον παρατηρητή Β  είναι  υ_ηχ + υ  ( υ_ηχ , υ  αντίρροπα διανύσματα )     

           λ_Α  =   (υ_ηχ - υ) / f_s  =  (340 - 34) / 680  =  0,9 340 / 680  =  0,9 / 2  =  0,45 m

           λ_B  =   (υ_ηχ + υ) / f_s  =  (340 + 34) / 680  =  1,1 340 / 680  =  1,1 / 2  =  0,55 m

ο Α αντιλαμβάνεται συχνότητα :    f_Α  =  f_s  ((υ_ηχ - υ) - υ) / ((υ_ηχ - υ) - υ)   =   f_s 

    ο Α απομακρύνεται από την πηγή  με ταχύτητα υ ,   η πηγή πλησιάζει τον Α με ταχύτητα υ 

ο Β αντιλαμβάνεται συχνότητα :    f_Β  =  f_s  ((υ_ηχ + υ) + υ) / ((υ_ηχ + υ) + υ)   =   f_s 

    ο Β πλησιάζει την πηγή  με ταχύτητα υ ,   η πηγή απομακρύνεται από τον Β με ταχύτητα υ 

B11.   Σε κινούμενο  προς τα αριστερά  όχημα (1) με ταχύτητα υ₁ = υ/10  υπάρχει ηχητική πηγή που εκπέμπει ήχο συχνότητας fs.  Οχημα (2) κινείται με ταχύτητα  υ₂ = υ/5  αντίθετης φοράς (προς τα δεξιά).   Στο όχημα (1) υπάρχει συσκευή ανίχνευσης των  ανακλώμενων στο όχημα (2) ηχητικών κυμάτων.  Η ταχύτητα του ήχου ως προς τον ακίνητο αέρα είναι υ.  ( ο ανακλώμενος ήχος στο όχημα (2) έχει την ίδια συχνότητα με τον προσπίπτοντα σε αυτόν ήχο ).  Η συχνότητα f1  του ήχου που ανιχνεύει η συσκευή, είναι
α)  f1 = 6fs/11         β)  f1 = 121fs/81            γ)  f1 = 8fs/11             δ)  f1 = fs/2

παρατηρητής Α  στο όχημα (2)  αντιλαμβάνεται συχνότητα   f_Α  =  f_s  ( υ_ηχ - υ₂ ) / ( υ_ηχ + υ₁ )   => 

      =>      f_Α  =  f_s  ( υ - υ/5 ) / ( υ + υ/10 )   =    f_s  4υ/5  /  11υ/10    =   8/11  f_s   

               η ταχύτητα του ήχου ως προς τον Α  είναι :   ( υ_ηχ - υ₂ )    επειδή  υ_ηχ  και  υ₂  είναι  ομόρροπα διανύσματα

                      ο Α  αντιλαμβάνεται μήκος κύματος :  λ_Α  =  λ  +  υ₁ T  =  υ_ηχ Τ  +  υ₁ Τ  =  ( υ_ηχ  +  υ₁ ) / f_s 

   επαλήθευση :  λ_Α  f_Α  =  ( υ_ηχ  +  υ₁ ) / f_s    f_s  ( υ_ηχ - υ₂ ) / ( υ_ηχ + υ₁ )  = ( υ_ηχ - υ₂ ) ταχύτητα του ήχου ως προς Α

το όχημα (2) γίνεται πηγή ηχητικών κυμάτων  και  ο ανακλώμενος ήχος έχει την ίδια συχνότητα  f_Α    οπότε ο δέκτης κυμάτων στο  όχημα (1)  ανιχνεύει  συχνότητα

 f₁  =  f_Α  ( υ_ηχ - υ/10 ) / ( υ_ηχ + υ/5 )   =   8/11  f_s  ( υ - υ/10 ) / ( υ + υ/5 )  =   8/11 f_s  9υ/10  /  6υ/5   =   8/11  f_s  3/4   =>     f₁   =  6/11 f_s      ο δέκτης στο όχημα (1)  απομακρύνεται   το όχημα (2) απομακρύνεται

Β12.    Στο προηγούμενο πρόβλημα τα οχήματα κινούνται αντίθετα και πλησιάζουν με ταχύτητες  υ₁  και  υ₂  αντίστοιχα.  Ο παρατηρητής Α που κάθεται ακίνητος ανάμεσα στα δύο οχήματα ακούει από ανάκλαση στο όχημα (2) ήχο με μήκος κύματος ίσο με

α. λ_Α = (υ-υ2)(υ-υ1) / (υ+υ2)fs           β. λ_Α = (υ-υ1)(υ+ υ2) / (υ+υ2)fs                   γ. λ_Α = (υ+υ1)(υ-υ1) / (υ+υ2)fs  

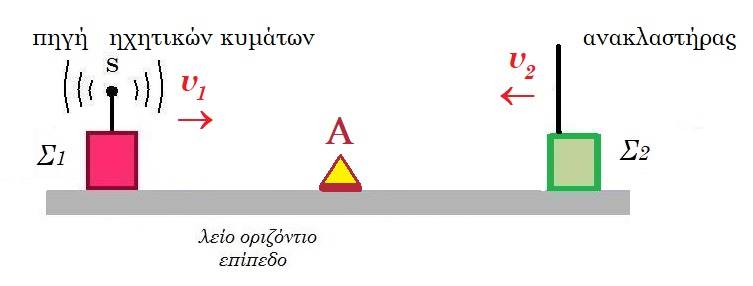
παρατηρητής Β  στο όχημα (2)  αντιλαμβάνεται συχνότητα   f_Β  =  f_s  ( υ_ηχ + υ₂ ) / ( υ_ηχ - υ₁ )  

το όχημα (2) γίνεται πηγή ηχητικών κυμάτων  και  ο ανακλώμενος ήχος έχει την ίδια  συχνότητα  f_Β    οπότε ο  παρατηρητής Α   ανιχνεύει  συχνότητα

      f_Α  =  f_Β  υ_ηχ / ( υ_ηχ - υ₂ )   =     f_s  ( υ_ηχ + υ₂ ) / ( υ_ηχ - υ₁ )   υ_ηχ / ( υ_ηχ - υ₂ )   => 

    =>        f_Α / υ_ηχ   =   f_s  ( υ_ηχ + υ₂ ) / ( υ_ηχ - υ₁ ) ( υ_ηχ - υ₂ )   => 

    =>       υ_ηχ /  f_Α   =   λ_Α   =   ( υ_ηχ - υ₁ ) ( υ_ηχ - υ₂ )  / ( υ_ηχ + υ₂ )f_s  

      ο ακίνητος παρατηρητής Α  αντιλαμβάνεται  ηχητικά κύματα απευθείας από την πηγή

     με μήκος κύματος :  λ_Α  =  λ  -  υ₁ Τ  =  υ_ηχ Τ - υ₁ Τ =   ( υ_ηχ - υ₁ ) / f_s 

    και  συχνότητα :  f_A  =  f_S  υ_ηχ / ( υ_ηχ - υ₁ )                η ταχύτητα του ήχου ως προς τον Α  είναι :  υ_ηχ =  λ_Α  f_A  

B13.   Το σύστημα του σχήματος ταλαντώνεται με εξίσωση απομάκρυνσης  x(t) = 0,4 ημ(5t + π/2)  (S.I.).  (θετική φορά προς τα πάνω).   Η πηγή S που είναι προσαρμοσμένη στο ελατήριο εκπέμπει ήχο συχνότητας fs = 684 Ηz, ταχύτητας υ=340m/s. Ο παρατηρητής που βρίσκεται στη θέση Α ακούει τον ήχο με ελάχιστη συχνότητα
α)  688 Ηz       β)  684 Ηz       γ)  680 Ηz

Για ποιό μέγιστο πλάτος ταλάντωσης  του σώματος (1),  το σώμα (2)  χάνει την επαφή του με το οριζόντιο επίπεδος;   Ποιά συχνότητα f_Α  ανιχνεύει ο παρατηρητής Α συναρτήσει του χρόνου για πλάτος ταλάντωσης που βρήκατε;   Οι μάζες των σωμάτων :  m₁ = 1 kg ,   m₂ = 2 kg

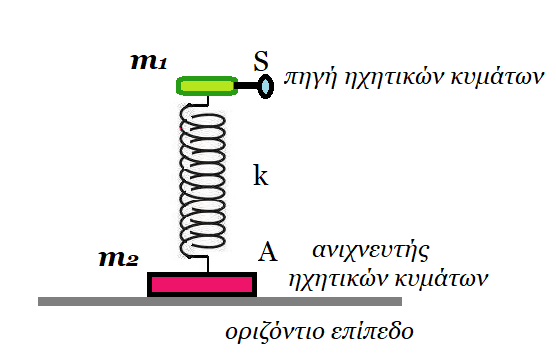
το σώμα (1)  ταλαντώνεται  με συχνότητα  f = ω/2π  =  5/2π Hz    η περίοδος της ταλάντωσης είναι  Τ = 1/f  =  0,4π s

το πλάτος ταλάντωσης είναι  Α = 0,4 m        x = 0,4 ημ(5t + π/2)       υ = 2 συν(5t + π/2)         α = - 10 ημ(5t + π/2)  

ο ακίνητος ανιχνευτής  καταγράφει  συχνότητα :    f_Α  =  f_s  υ_ηχ  / ( υ_ηχ + υ₁ )  =  684  340 / ( 340 + 2 συν(5t + π/2) )    

 η ελαχιστη συχνότητα συμβαίνει όταν  συν(5t + π/2) = +1   οπότε έχουμε :  

                      f_Α,ελαχ  =   684  340 / ( 340 + 2 )  =  684 340 / 342  =  2  340  =  680 Hz

 η μέγιστη συχνότητα συμβαίνει όταν  συν(5t + π/2) = -1  οπότε έχουμε : 

                     f_Α,μέγ  =  684  340 / ( 340 - 2 )  =  684 340 / 338 Ηz

                          m₁  =  1 kg         m₂  =  2 kg             k  =  m₁  ω²  =  25 N/m   σταθερά ελατηρίου                     

 θέση ισορροπίας  σώματος (1) :  m₁ g  = k x₀  =>   1 10  = 25 x₀    =>   x₀  = 0,4 m   συσπείρωση    (Θ.Ι.)     

  ΣF  =  m₁ α   =>   F_ελατ  -  m₁ g  =  m₁ α   =>   F_ελατ  - 10  = - 10 ημ(5t + π/2)   =>   F_ελατ(t) = 10 - 10 ημ(5t + π/2) 

 το σώμα (2)  δέχεται δυνάμεις :   ΣF  =  0  =>   F_ελατ  -  m₂ g  +  Ν  =  0   =>  - 10 + 10 ημ(5t + π/2)  - 20  + Ν  =  0   =>   Ν  =  10  - 10 ημ(5t + π/2)  +  20    =>     Ν(t)  =  30  - 10 ημ(5t + π/2)   αντίδραση από το οριζόντιο επίπεδο

   t = 0      F_ελατ  =  10 - 10  =  0            Ν  =  30  - 10 ημ(π/2)  =  30 - 10 = 20 Ν  =  m₂ g 

  το σώμα (1)  είναι στην άνω ακραία θέση της ταλάντωσής του  και  το ελατήριο έχει το φυσικό του μήκος

  t = T/4 =  0,4π / 4  =  π/10 s            F_ελατ  =  10 - 10 ημ(5 π/10  + π/2)  =  10 - 10 ημ(π/2  + π/2)  = 10 N    

        Ν  =  30  - 10 ημ(5 π/10 + π/2)   =   30 Ν  

το σώμα (1)  διέρχεται από τη θέση ισορροπίας του  με ταχύτητα αρνητική (προς τα κάτω)  και  η δύναμη του ελατηρίου είναι αντίθετη του βάρους του

  t = T/2 =  0,4π / 2  =  0,2π s        F_ελατ =  10 - 10 ημ(5 0,2π  + π/2)  =  10 - 10 ημ(π + π/2)  =  10 - 10 (-1) =  20 N   

            Ν  =  30  - 10 ημ(5 0,2π + π/2)   =  30 - 10 (-1) =   40 Ν  

το σώμα (1)  διέρχεται από τη  κάτω ακραία θέση της ταλάντωσής του   και  η δύναμη του ελατηρίου είναι μέγιστη

  t = 3T/4 = 3 0,4π / 4  = 0,3π s      F_ελατ  =  10 - 10 ημ(5 0,3π  + π/2)  =  10 - 10 ημ(2π)  =  10 N   

          Ν  =  30  - 10 ημ(5 0,3π + π/2)   =  30 - 10 ημ(2π)  =   30 Ν  

  το σώμα (1)  διέρχεται από τη θέση ισορροπίας του με ταχύτητα θετική (προς τα πάνω)  και  η δύναμη του ελατηρίου είναι αντίθετη του βάρους του

 η αντίδραση Ν  από το δάπεδο γίνεται  μηδέν  όταν το πλάτος ταλάντωσης του σώματος (1)  είναι  Α > 0,4 m

 τότε   x(t)  =  Α ημ(5t + π/2)             υ(t)  =  5Α συν(5t + π/2)             α(t)  =  - 25Α ημ(5t + π/2) 

  ΣF  =  m₁ α   =>   F_ελατ  -  m₁ g  =  m₁ α    =>   F_ελατ  - 10  =  - 25Α ημ(5t + π/2)   => 

                                                                     =>   F_ελατ(t) =  10 - 25Α ημ(5t + π/2) 

 το σώμα (2)  δέχεται δυνάμεις :   ΣF  =  0  =>   F_ελατ  -  m₂ g  +  Ν  =  0   =>  - 10 + 25Α ημ(5t + π/2)  - 20  + Ν =  0   =>   Ν  =  10  - 25Α ημ(5t + π/2)  +  20    =>     Ν(t)  =  30  - 25Α ημ(5t + π/2)   

  η μικρότερη τιμή της Ν  είναι όταν   ημ(5t + π/2) = +1   τότε  Ν = 30 - 25Α    

 το σώμα (2)  χάνει την επαφή του με το δάπεδο :   Ν = 0  =>   30  - 25Α =  0   =>    Α = 30/25 m  =  1,2 m 

πράγματι για αυτό το πλάτος ταλάντωσης του σώματος (1)  και  επειδή στη θέση ισσορροπίας του  το ελατήριο είναι συσπειρωμένο κατά  0,4 m ,  στην κάτω ακραία θέση του σώματος (1)  το ελατήριο είναι συσπειρωμένο κατά  0,4 + 1,2 = 1,6 m    ενώ  στην άνω ακραία θέση του σώματος (1)  το ελατήριο είναι  επιμηκυμένο κατά  1,2 - 0,4 = 0,8 m    οπότε η δύναμη ελατηρίου που ασκείται στο σώμα (1) είναι  F_ελατ =  25 N/m  0,8 m  =  20 N  με φορά προς τα κάτω (αρνητική κατεύθυνση)   ενώ  το σώμα (2)  δέχεται  F_ελατ =  25 N/m  0,8 m  =  20 N  με φορά προς τα πάνω (θετική κατεύθυνση)   τότε  F_ελατ =  20 N  =  2 kg  10 m/s²  =  m₂ g     δηλαδή  η αντίδραση  Ν = 0   

    όταν   ημ(5t + π/2) = +1          άνω ακραία θέση

τότε  F_ελατ  = 10 - 25Α ημ(5t + π/2)  =  10  -  25 1,2 (+1)  =  10 - 30 =  - 20 Ν  ασκείται στο σώμα (1)  

        F_ελατ  = - 10 + 25Α ημ(5t + π/2)  =  - 10  +  25 1,2 (+1)  =  - 10 + 30 =  - 20 Ν  ασκείται στο σώμα (2)  

        Ν  =  30  - 25Α ημ(5t + π/2)  =  30  -  25 1,2 (+1)  =  30 - 30 = 0

    όταν   ημ(5t + π/2) = - 1          κάτω ακραία θέση

τότε  F_ελατ  = 10 - 25Α ημ(5t + π/2)  =  10  -  25 1,2 (-1)  =  10  + 30 =  + 40 Ν  ασκείται στο σώμα (1)  

        F_ελατ  = - 10 + 25Α ημ(5t + π/2)  =  - 10  +  25 1,2 (-1)  =  - 10  - 30 =  - 40 Ν  ασκείται στο σώμα (2)  

        Ν  =  30  - 25Α ημ(5t + π/2)  =  30  -  25 1,2 (-1)  =  30 + 30 =  60 Ν             

 τότε   x(t)  =  1,2 ημ(5t + π/2)             υ(t)  =  6 συν(5t + π/2)             α(t)  =  - 30 ημ(5t + π/2)   

  F_ελατ(t) =  10 - 30 ημ(5t + π/2)   ασκείται στο σώμα (1)    

    F_ελατ(t) =  - 10  + 30 ημ(5t + π/2)    ασκείται στο σώμα (2)           Ν(t)  =  30  - 30 ημ(5t + π/2)          

η συχνότητα που ανιχνεύει ο παρατηρητής Α :    f_Α =  f_s  υ_ηχ  / ( υ_ηχ + υ₁ )  =  684  340 / ( 340 + 6 συν(5t + π/2) )  

 η ελαχιστη συχνότητα συμβαίνει όταν  συν(5t + π/2) = +1   οπότε έχουμε :  

                      f_{Α,ελάχιστη}  =   684  340 / ( 340 + 6 )  =  684 340 / 346  Hz

 η μέγιστη συχνότητα συμβαίνει όταν  συν(5t + π/2) = -1  οπότε έχουμε : 

                     f_{Α,μέγιστη}  =  684  340 / ( 340 - 6 )  =  684 340 / 334 Ηz

Β14.   Παρατηρητής Α πλησιάζει προς ακίνητη πηγή με ταχύτητα που μεταβάλλεται σύμφωνα με τη σχέση υ=5t. Η πηγή εκπέμπει ήχο συχνότητας fs=680Ηz που τρέχει στον αέρα με ταχύτητα υ=340Ηz. Ο αριθμός των παλμών που ακούει ο παρατηρητής από τη χρονική στιγμή t1=2s έως τη χρονική στιγμή t2=10s είναι:       α. 5920          β. 7300              γ. 8000

υ_A = 5t        f_A  =  f_S  ( v + 5t ) / v  =  680  ( 340 + 5t ) / 340  =  2 ( 340 + 5t )  =  680 + 10t  =  dN/dt  =  N'(t) 

            t = 2 s    f_A  =  680 + 20 =  700 Hz  =  700 παλμοί/sec        

           t = 10 s    f_A  =  680 + 100 =  780 Hz  =  780 παλμοί/sec                  

dN/dt  =  680 + 10t  =>   dN =  (680 + 10t) dt  =>  N = [ 680t  +  5t²]_{t=2s => 10s} = 680 ( 10 - 2 ) + 5 ( 10² - 2² ) 

       =>  N  =  680  8  +  5 ( 100 - 4 )  =  5440  + 480  =  5920 παλμοί    από  2s   εώς  10s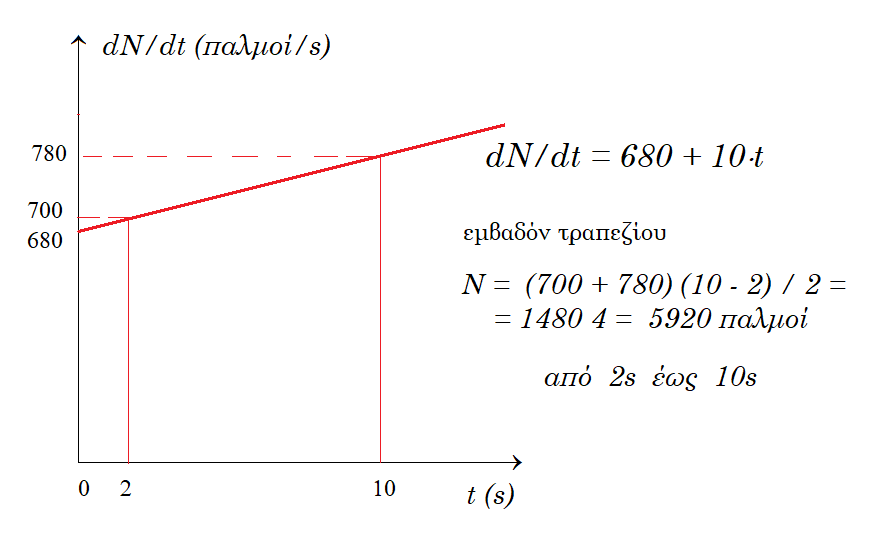     

Β15.   Hχητική πηγή πλησιάζει προς ένα ακίνητο παρατηρητή με ταχύτητα υs=40m/s και εκπέμπει ήχο με συχνότητας fs=3000Ηz για χρονική διάρκεια Δt=3,4s. Ο παρατηρητής ακούει τον ήχο για χρονική διάρκεια :       α.  3,4s             β.  3s            γ.  2,7s              δ.  4s 

       από την πηγή εκπέμπονται  Ν  =  f_S  t  =  3000 Hz  3,4 s  =  10200 παλμοί 

     f_A  =  f_S  v / (v - v_S)  =  3000   340 / (340  - 40)  =  3400 Hz  

  ο παρατηρητής δέχεται  10200 παλμούς  συχνότητας  3400 Hz  σε χρονικό διάστημα  Δt  =  10200 παλμούς / 3400 Hz  =  3 sec

Β16.   Το ακίνητο Radar της τροχαίας εκπέμπει κύματα συχνότητας f1 προς αυτοκίνητο που απομακρύνεται από αυτό με ταχύτητα υα.   Τα κύματα ανακλώνται στο αυτοκίνητο και επιστρέφουν στο Radar με συχνότητα f2.   Η ταχύτητα των κυμάτων ως προς τον αέρα είναι υ.
Ι.   Αν η σχέση των δύο συχνοτήτων είναι f2/f1=9/11 τότε η ταχύτητα του αυτοκινήτου είναι :
α.  υα = υ/5              β.  υα = υ/6             γ.  υα = 2υ/5                  δ.  υα = υ/10
ΙΙ.  Το μήκος κύματος του ήχου από ανάκλαση που καταγράφει το Radar είναι
α.  λ = 11υ / 9f1              β.  λ = 9υ / 11f1             γ.  λ = 10υ / 9f1                δ.  λ = 11υ /10f1      

η ταχύτητα των κυμάτων ως προς τον οδηγό του αυτοκινήτου  είναι :  υ - υ_α   διότι τα διανύσματα  υ  και  υ_α  είναι ομόρροπα

  ο οδηγός αντιλαμβάνεται μήκος κύματος :  λ_α  =  λ  =  υ / f₁     και   συχνότητα κυμάτων :    f_a  =  f₁  ( υ - υ_α ) / v 

τα κύματα ανακλώνται στο αυτοκίνητο  το οποίο γίνεται  πηγή κυμάτων  με την ίδια συχνότητα  f_a = f₁ ( υ - υ_α ) / v   και  φθάνουν στο  ακίνητο Radar   το οποίο αντιλαμβάνεται  συχνότητα :   f₂  =  f_a  v / ( v + v_a )  =  f₁ ( υ - υ_α )/( υ + υ_α )

  f₂ / f₁  =  ( υ - υ_α )/( υ + υ_α )  =>   9/11  =  ( υ - υ_α )/( υ + υ_α )  =>   9 ( υ + υ_α ) = 11 ( υ - υ_α ) =>   v = 10 v_a 

    συνεπώς :  f_a  =  f₁  ( υ - υ_α ) / v  =  0,9 f₁  το ανακλώμενο κύμα έχει μήκος κύματος  λ' =  υ / f_a  =  v² / ( υ - υ_α )f₁  

παρατηρητής τώρα είναι το ακίνητο Radar  που αντιλαμβάνεται μήκος κύματος :

    λ₂  f₂  =  υ  =>    λ₂  9/11 f₁  =  υ  =>   λ₂  =  11υ / 9f₁ 

λ₂  =   λ'  +   υ_α / f_a   =                  άλλος τρόπος                  

     =   v² / ( υ - υ_α )f₁   +   υ_α / [ f₁ ( υ - υ_α ) / v ]  =   v² / ( υ - υ_α )f₁   +   υ υ_α / ( υ - υ_α )f₁    = 

    =   υ( υ  +  υ_α ) /( υ - υ_α )f₁    =   υ 11υ_α ) / 9υ_α f₁   =  11υ / 9f₁