κύμα οδεύει προς τα αρνητικά του άξονα
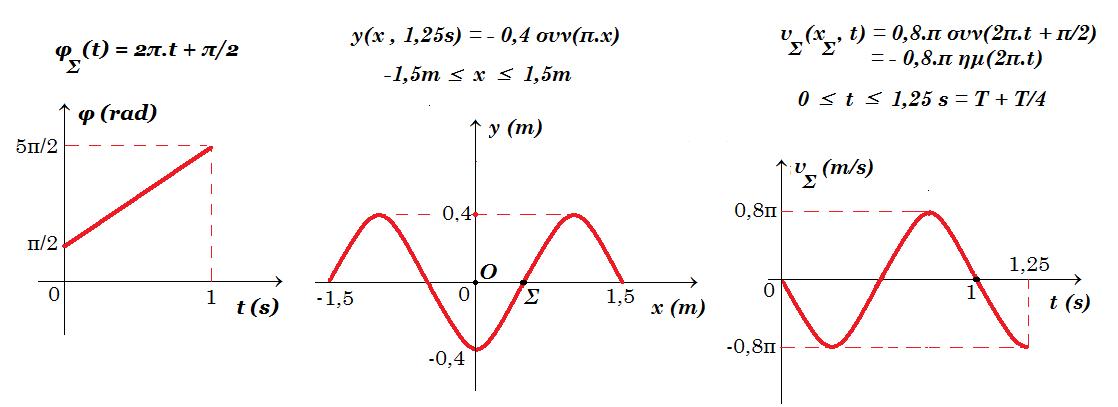
Κατά μήκος ενός γραμμικού ελαστικού μέσου διαδίδεται ένα αρμονικό κύμα με ταχύτητα υ=2m/s, προς τα αριστερά. Παίρνοντας έναν προσανατολισμένο άξονα x΄x με θετική φορά προς τα δεξιά και αρχή ένα σημείο Ο, τη στιγμή t=0, το κύμα φτάνει σε ένα σημείο Σ, στη θέση xΣ=1,5m, ενώ τη στιγμή αυτή, το μέσον εμφανίζει τη μορφή που δείχνει το σχήμα.
(α) Να γραφεί η εξίσωση της απομάκρυνσης του σημείου Σ, σε συνάρτηση με το χρόνο (y=f(t)).
(β) Να βρεθεί η εξίσωση του κύματος.
(γ) Να σχεδιάσετε το στιγμιότυπο του κύματος την χρονική στιγμή t1=1,5s.
(δ) Να κάνετε τις γραφικές παραστάσεις σε συνάρτηση με το χρόνο, για την απομάκρυνση (y=f(t)) και την ταχύτητα (υ=f(t)), ενός σημείου Β στην θέση xΒ=1m.
λ = 3,5 - 1,5 = 2 m v = λ / T => T = 1 s f = 1 Hz A = 0,4 m
y(xΣ , t) = 0,4 ημ(2π.t/1 + 2π.1,5/2) => y(xΣ , t) = 0,4 ημ(2π.t + 3π/2) = - 0,4 συν(2π.t)
y(x,t) = 0,4 ημ(2π.t/1 - 2π.x/2)
Κατά μήκος ενός γραμμικού ελαστικού μέσου, πολύ μεγάλου μήκους, διαδίδεται από αριστερά προς τα δεξιά (θετική φορά) ένα αρμονικό κύμα, πλάτους Α=0,4m και μήκους κύματος λ=2m, με ταχύτητα υ=2m/s. Στο διπλανό σχήμα βλέπετε μια μικρή περιοχή του κύματος (το οποίο έχει διαδοθεί πολύ πέρα του δεξιού άκρου του σχήματος). Για να γράψουμε εξίσωση για το κύμα αυτό, παίρνουμε ένα σύστημα αξόνων x,y με αρχή το σημείο Ο και θεωρούμε επίσης τη στιγμή που έχουμε το παραπάνω στιγμιότυπο, ως αρχή μέτρησης των χρόνων (t0=0).
- Με βάση τις παραπάνω παραδοχές, να βρεθεί η εξίσωση του κύματος, για το παραπάνω κύμα.
- Ποια η φάση της απομάκρυνσης των σημείων Ο και Σ τη στιγμή t0=0;
- Να κάνετε τη γραφική παράσταση της φάσης της απομάκρυνσης του σημείου Σ, σε συνάρτηση με το χρόνο (φ=f(t)).
- Να σχεδιάστε το στιγμιότυπο του κύματος τη χρονική στιγμή t1=1,25s, για την ίδια περιοχή του μέσου.
- Να παραστήσετε επίσης γραφικά την ταχύτητα ταλάντωσης του σημείου Σ σε συνάρτηση με το χρόνο, από t0 έως t1.
(1) A = 0,4 m λ = 2 m
v = λ f => 2 m/s = 2 m f => f = 1 Hz T = 1/f = 1 s ω = 2πf = 2.π rad/s
Αφού το κύμα διαδίδεται προς τα δεξιά, μετά από λίγο το σημείο Ο, στην αρχή των αξόνων, θα βρεθεί με
αρνητική απομάκρυνση (θα κινηθεί προς τα κάτω στο σχήμα). Αλλά αυτό σημαίνει ότι τη στιγμή t0=0
περνά από τη θέση ισορροπίας του κινούμενο προς την αρνητική κατεύθυνση και παρουσιάζει αρχική
φάση ίση με π (rad).
y(x,t) = 0,4 ημ(2π.t/1 - 2π.x/2 + π) => y(x,t) = 0,4 ημ(2π.t - π.x + π)
v(x,t) = 0,8.π συν(2π.t - π.x + π) α(x,t) = - 1,6.π2 ημ(2π.t - π.x + π) = - 16 ημ(2π.t - π.x + π)
(2) xO = 0 xΣ = λ/4 = 0,5 m φO(t) = 2π.t + π φΣ(t) = 2π.t - π/2 + π = 2π.t + π/2
(3) φΣ(0) = π/2 φΣ(t) = 0 => t = - 1/4 s = - T/4
(4) y(x , 1,25s) = 0,4 ημ(2π.1,25 - π.x + π) = 0,4 ημ(5π/2 - π.x + π) = - 0,4 συν(π.x)
(5) υΣ (xΣ , t) = 0,8.π συν(2π.t + π/2) = - 0,8.π ημ(2π.t) 0 £ t £ 1,25 s = T + T/4
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Κύμα εγκάρσιο διαδίδεται από αριστερά προς τα δεξιά. Στα γραφήματα φαίνεται το κύμα τις χρονικές στιγμές t1 t2 = t1 + 0,5s. Βρείτε την εξίσωση του κύματος.
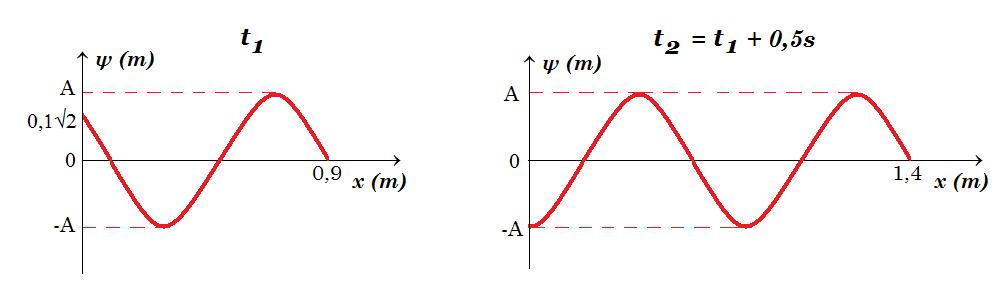
x2 = 1,4 m = 3λ/2 + λ/4 => 7λ/4 = 1,4 m => λ = 0,8 m
x1 = 0,9 m = λ + λ/8
v = x1 / t1 = x2 / (t1 + 0,5) = (3λ/2 + λ/4) / (t1 + 0,5)
x1 / t1 = x2 / (t1 + 0,5) => 0,9 / t1 = 1,4 / (t1 + 0,5) => 0,9 (t1 + 0,5) = 1,4 t1 => t1 = 0,9 s
t2 = 1,4 s v = 1 m/s T = λ / v = 0,8 s
y(x,t1) = Α ημ(2π.t/T - 2π.x/λ) => y(x,t) = 0,2 ημ(2π.t/0,8 - 2π.x/0,8) = 0,2 ημ(2π/0,8).(t - x) => y(x,t) = 0,2 ημ2,5π.(t - x)
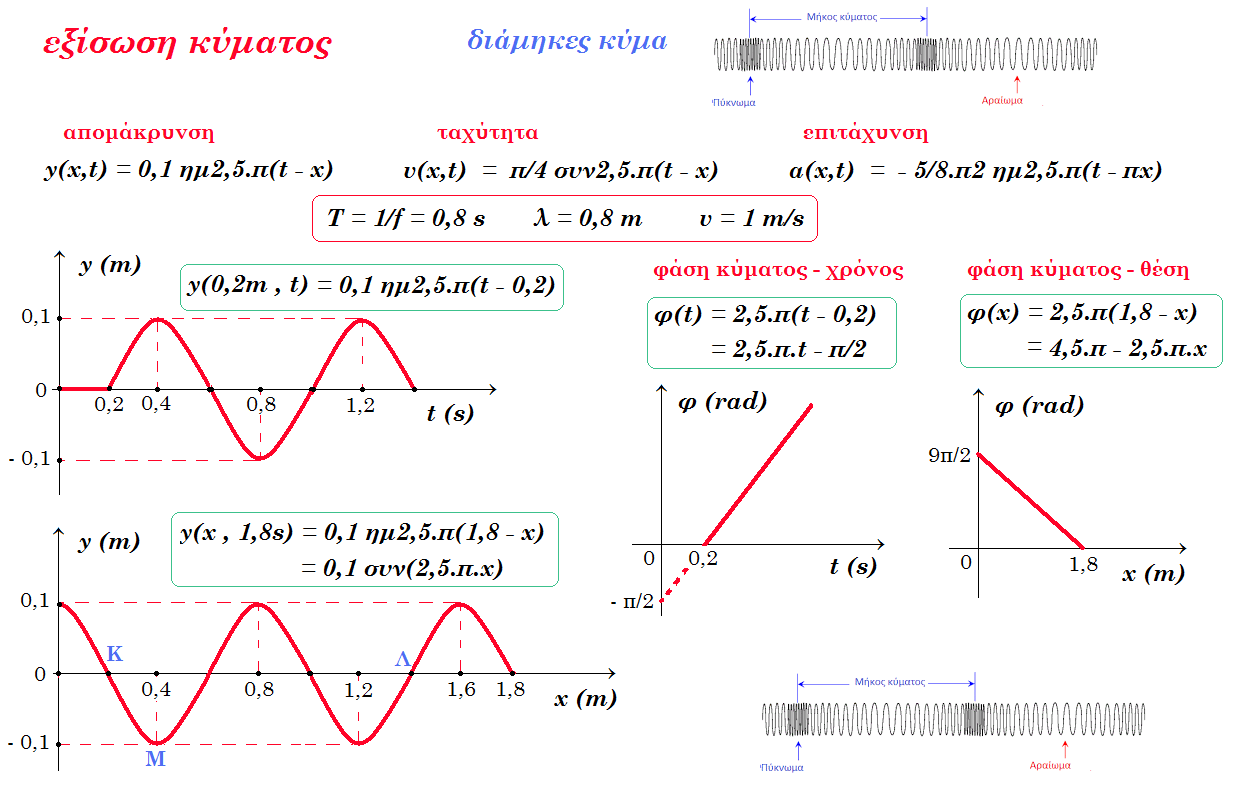
Διάμηκες αρμονικό κύμα διαδίδεται σε ελαστικό μέσο. Ένα σημείο του ελαστικού μέσου διέρχεται 10 φορές από τη θέση ισορροπίας του σε χρονικό διάστημα Δt=4s. Οι ακραίες θέσεις της ταλάντωσης κάθε σημείου απέχουν d=0,2m. Ένα πύκνωμα απέχει από το μεθεπόμενο αραίωμα απόσταση s=1,2m.
α) Να γραφεί η εξίσωση του κύματος.
β) Να γίνει η γραφική παράσταση της απομάκρυνσης ως προς τον χρόνο για ένα σημείο Κ όπου xK=0,2m.
γ) Να γίνει η γραφική παράσταση της απομάκρυνσης ως προς x τη χρονική στιγμή t1=1,8s.
δ) Σημείο Μ του ελαστικού μέσου με xΜ=0,4m έχει μεγαλύτερη φάση από την φάση του σημείου Λ κατά 5π/2. Να βρεθεί η απόσταση των σημείων Μ και Λ τη χρονική στιγμή t1=1,8s.
ε) Να γίνει η γραφική παράσταση της φάσης φ(t) για το σημείο Κ.
στ) Να γίνει η γραφική παράσταση της φάσης φ(x) τη χρονική στιγμή t1=1,8s.
(α) f = 5 / 4 = 1,25 Hz T = 1/f = 0,8 s ω = 2πf = 2,5.π rad/s 2A = 0,2 m => A = 0,1 m
λ + λ/2 = 1,2 => λ = 0,8 m v = λ f = 0,8 m 5/4 Hz = 1 m/s
y(x,t) = 0,1 ημ 2π (t/0,8 - x/0,8) => y(x,t) = 0,1 ημ2,5.π(t - x)
v(x,t) = π/4 συν2,5.π(t - x) α(x,t) = - 5/8.π2 ημ2,5.π(t - πx)
(β) y(0,2m , t) = 0,1 ημ2,5.π(t - 0,2) t ³ 0,2 s
y(0,2m , t) = 0,1 ημ2,5.π(t - 0,2) = 0,1 ημ(2,5.π.t - 0,5.π) => y(0,2m , t) = - 0,1 συν(2,5.π.t)
(γ) y(x , 1,8s) = 0,1 ημ2,5.π(1,8 - x) = 0,1 ημ(4,5.π - 2,5.π.x) = 0,1 συν(2,5.π.x)
(δ) φΜ - φΛ = 5π/2 => 2,5.π(t - xΜ ) - 2,5.π(t - xΛ ) = 5π/2 => - xΜ + xΛ = 1 m =>
=> xΛ = xΜ + 1 m = 0,4 m + 1 m => xΛ = 1,4 m
y(0,4m , 1,8) = 0,1 ημ2,5.π(1,8 - 0,4) = 0,1 ημ(2,5.π.1,4) = 0,1 ημ(3π + π/2)) = - 0,1 m
y(1,4m , 1,8) = 0,1 ημ2,5.π(1,8 - 1,4) = 0,1 ημ(2,5.π.0,4) = 0,1 ημ(π) = 0
επειδή το κύμα είναι διάμηκες τη στιγμή t = 1,8 s το σημείο Λ βρίσκεται στη θέση ισορροπίας του και το σημείο Μ σε απομάκρυνση - 0,1 m οπότε η απόστασή τους είναι 1 m + 0,1 m = 1,1 m
(ε) y(0,2m , t) = 0,1 ημ2,5.π(t - 0,2) φ(t) = 2,5.π(t - 0,2) = 2,5.π.t - π/2
(στ) y(x , 1,8s) = 0,1 ημ2,5.π(1,8 - x) φ(x) = 2,5.π(1,8 - x) = 4,5.π - 2,5.π.x
Μια πηγή μικρών διαστάσεων εκπέμπει ηχητικά κύματα στον αέρα. Η ισχύς του ηχητικού κύματος που εκπέμπει η πηγή είναι 𝑃0 = 1 𝑊 και η συχνότητα του ηχητικού κύματος που εκπέμπει είναι 1100 Hz. Δίνεται ότι η ταχύτητα του ήχου στον αέρα 343 m/s.
(α) Να αναφέρετε πόση θα είναι η ταχύτητα διάδοσης του ηχητικού κύματος που εκπέμπεται από την ίδια ηχητική πηγή, αν η συχνότητά του γίνει 550 Hz.
(β) Να υπολογίσετε την ένταση του ηχητικού κύματος σε απόσταση 5 m από την πηγή.
(γ) Να υπολογίσετε τη μεταβολή του επιπέδου έντασης του ήχου αν η απόσταση από την πηγή μεταβληθεί από 5 m σε 10 m.
v = λ f v = 343 m/s σταθερή ταχύτητα στον αέρα
I = P / S = P / 4πr2 => I = 1W / 4π 25m2 = 1/314 W/m2
I' = 1W / 4π 100m2 = 1 / (4 314) W/m2 I / I' = 4
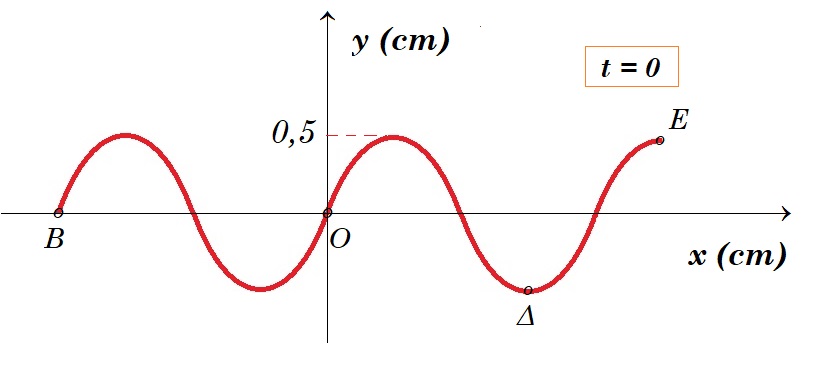
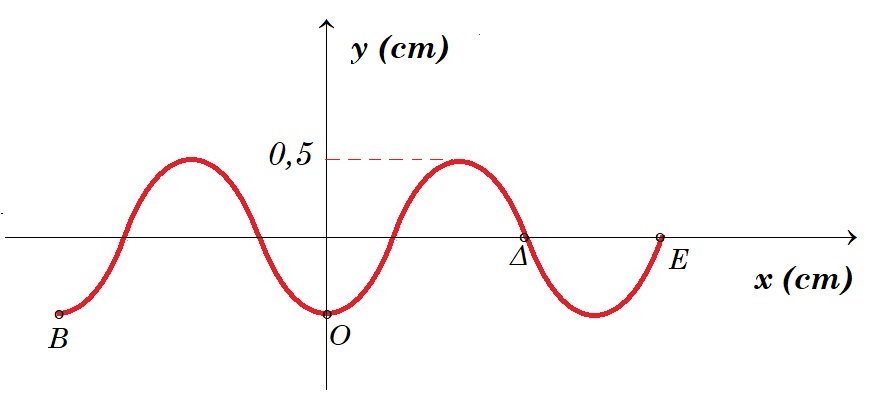
Ένα κύμα διαδίδεται προς τα δεξιά (θετική κατεύθυνση) κατά μήκος ενός γραμμικού ελαστικού μέσου. Στο σχήμα δίνεται ένα τμήμα του μέσου, μεταξύ των σημείων Β και Ε, σε κάποια χρονική στιγμή την οποία θεωρούμε t = 0.
Να θεωρήσετε ότι τη χρονική στιγμή t = 0 τα σημεία Δ και Ε έχουν μηδενική ταχύτητα ταλάντωσης. Το σημείο Ο, στη θέση x = 0, θα φτάσει για πρώτη φορά σε απομάκρυνση 0,5 cm τη χρονική στιγμή t1 = 0,3 s.
(α) Να υπολογίσετε την αλγεβρική τιμή της ταχύτητας ταλάντωσης του σημείου Ο τη χρονική στιγμή που ελήφθη το παραπάνω στιγμιότυπο.
(β) Να σχεδιάσετε το στιγμιότυπο του κύματος για την ίδια περιοχή, τη χρονική στιγμή t2 = 0,1 s. Στο στιγμιότυπο να φαίνονται οι θέσεις των σημείων Β, O, Δ και Ε.
το σημείο Ο αμέσως μετά τη στιγμή t=0 θα κινηθεί προς τα κάτω θα φθάσει σε απομάκρυση y = - 0,5 cm σε χρονικό διάστημα Τ/4 μετά θα κινηθεί προς τα επάνω και θα φθάσει σε απομάκρυση y = + 0,5 cm σε χρονικό διάστημα Τ/2 οπότε : 3T/4 = 0,3 s => T = 0,4 s περίοδος ταλάντωσης του σημείου Ο
f = 1/T = 1/0,4 = 2,5 Hz ω = 2π/Τ = 2π/0,4 => ω = 5π rad/s
v = ω A = 5π rad/s 0,5 cm => v = 25π mm/s
0,1 s = T/4
Κατά μήκος ενός γραμμικού ελαστικού μέσου διαδίδεται προς την θετική κατεύθυνση ένα αρμονικό κύμα, πλάτους Α=0,4m με ταχύτητα 2m/s. Την χρονική στιγμή t=0, το κύμα φτάνει στην αρχή Ο ενός προσανατολισμένου άξονα, το οποίο αρχίζει να ταλαντώνεται, κινούμενο προς τα πάνω (θετική απομάκρυνση) με περίοδο Τ=2s.
(α) Να γράψετε την εξίσωση του διαδιδόμενου κύματος.
(β) Να σχεδιάσετε ένα στιγμιότυπο του κύματος την χρονική στιγμή t1=4,5s.
(γ) Ένα υλικό σημείο Σ του μέσου, με μάζα m=1g, βρίσκεται στην θέση x1=20/3m. Να υπολογίσετε την ταχύτητα του Σ και την συνισταμένη δύναμη που δέχεται από το μέσον, τις χρονικές στιγμές t1 και t2=2,8s.
(α) ω = 2π/Τ = 2π/2 = π rad/s v = λ/T => λ = v T = 2 m/s 2 s = 4 m
y(x,t) = 0,4 ημ 2π (t/2 - x/4) = 0,4 ημ(πt - πx/2) v(x,t) = 0,4π συν(πt - πx/2) α(x,t) = 0,4π2 ημ(πt - πx/2)
(β) y = 0,4 ημ π(4,5 - x/2) = 0,4 συν(πx/2) y = 0 => x = 9 m = 2 m/s 4,5 s = v t
Τ = 2s t1 = 4,5s = 2T + T/4 δύο περίοδοι + 1/4 της περιόδου
(γ) yΣ = 0,4 ημ π(t - (20/3)/2) => yΣ = 0,4 ημ π(t - 10/3) υΣ = 0,4π συν π(t - 10/3)
αΣ = - 4 ημ π(t - 10/3) π2 = 10 ΣF = m a = 0,001 ( - 4 ημ π(t - 10/3) ) = - 0,004 ημ π(t - 10/3) t = 20/3 m / 2 m/s = 10/3 s < 4,5 s
υΣ = 0,4π συν π(t - 10/3) = 0,4π συν π(4,5 - 10/3) = 0,4π συν(7π/6) = - 0,4π 3½/2 = - 0,2π 3½ m/s
ΣF = - 0,004 ημ π(t - 10/3) => ΣF = - 0,004 ημ(7π/6) = - 0,004 ( - ½ ) = + 0,002 Ν
την στιγμή 2,8 s το κύμα δεν έχει φθάσει στο σημείο Σ
ΘΕΜΑ Γ
Εγκάρσιο αρμονικό κύμα διαδίδεται χωρίς απώλειες ενέργειας σε γραμμικό ελαστικό μέσο (χορδή) που ταυτίζεται με τον ημιάξονα Οx, προς τη θετική κατεύθυνση. Η πηγή του κύματος βρίσκεται στο άκρο Ο (x=0) του ημιάξονα Οx του ελαστικού μέσου. Η πηγή εκτελεί απλή αρμονική ταλάντωση με εξίσωση απομάκρυνσης y=A∙ημωt.
Στοιχειώδης μάζα Δm = 10-6 kg του ελαστικού μέσου έχει ενέργεια ταλάντωσης ΕΤ = 5π2 10-7 J.
Το ελάχιστο χρονικό διάστημα για την απευθείας μετάβαση της στοιχειώδους μάζας Δm του ελαστικού μέσου από την κάτω ακραία θέση ταλάντωσής της μέχρι την επάνω ακραία θέση ταλάντωσής της είναι Δt=0,4s.
Στο ίδιο χρονικό διάστημα το κύμα έχει διαδοθεί σε απόσταση Δx=4cm.
Γ1. Να υπολογίσετε την περίοδο του κύματος, το μήκος κύματος του κύματος και το πλάτος ταλάντωσης της στοιχειώδους μάζας Δm.
Γ2. Να γράψετε την εξίσωση του αρμονικού κύματος και να σχεδιάσετε σε βαθμολογημένους άξονες το στιγμιότυπο του κύματος τη χρονική στιγμή t1=1,4s .
Γ3. Να υπολογίσετε την κινητική ενέργεια της στοιχειώδους μάζας Δm, όταν η απομάκρυνσή της από τη θέση ισορροπίας της είναι y=0,2m.
Δύο σημεία Ρ και Σ της χορδής έχουν διαφορά φάσης φΡ - φΣ = 3π/2 rad.
Γ4. Να υπολογίσετε την ταχύτητα του Σ, όταν η απομάκρυνση του σημείου Ρ από τη θέση ισορροπίας του είναι yΡ=0,4m.
Γ1) Δt = 0,4 s = T/2 => T = 0,8 s Δx = 0,04 m = λ/2 => λ = 0,08 m v = λ / T = 0,08 m / 0,8 s = 0,1 m/s
ω = 2π/Τ = 2π/0,8 = 20π/8 = 5π/2 rad/s
D = Δm ω2 = 10-6 (5π/2)2 = 25/4 π2 10-6 Ν/m
ET = ½ D A2 => 5π2 10-7 = ½ 25/4 π2 10-6 A2 => A2 = 4/25 => A = 2/5 = 0,4 m πλάτος ταλάντωσης
Γ2) y = A ημ ( 2πt/T - 2πx/λ ) => y = 0,4 ημ ( 2πt/0,8 - 2πx/0,08 ) =>
=> y = 0,4 ημ ( 20π/8 t - 200π/8 x ) => y(t,x) = 0,4 ημ ( 2,5π t - 25π x )
t = 1,4 s = 7/4 T : y(1,4 , x) = 0,4 ημ ( 5π/2 1,4 - 25π x ) = 0,4 ημ ( 7π/2 - 25π x ) = - 0,4 συν(25π x) 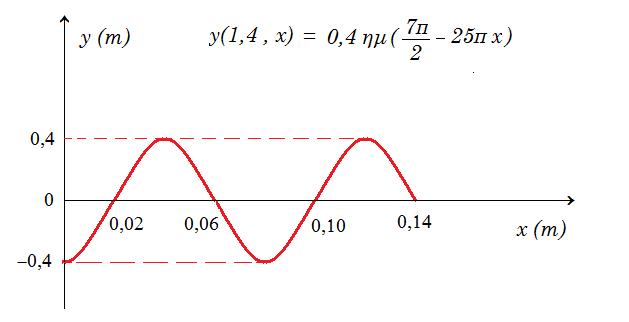
Γ3) K + U = E => K + ½ D y2 = ½ D A2 => K = ½ D A2 - ½ D y2 = ½ 25/4 π2 10-6 ( 0,42 - 0,22 ) =>
=> K = 25/8 π2 10-6 ( 0,16 - 0,04 ) = 0,12 25/8 π2 10-6 = 75/2 π2 10-8 J
Γ4) φΡ - φΣ = 3π/2 rad => ( 2,5π t - 25π xΡ ) - ( 2,5π t - 25π xΣ ) = 3π/2 => 25π xΣ - 25π xΡ = 3π/2
=> xΣ - xΡ = 3/50 = 0,06
yP = 0,4 m = 0,4 ημ ( 2,5π t - 25π xP ) => ημ ( 2,5π t - 25π xP ) = 1 => ημ φΡ = 1 =>
=> ημ ( 3π/2 + φΣ ) = 1 => - συν φΣ = 1 => συν φΣ = -1 => ημ φΣ = 0
yΣ (t,x) = 0,4 ημ ( 2,5π t - 25π xΣ ) = 0,4 ημ φΣ = 0,4 0 = 0
υΣ (t,x) = 0,4 2,5π συν ( 2,5π t - 25π xΣ ) = π συν φΣ = π (-1) = - π m/s
Β2. Δύο σύγχρονες πηγές κυμάτων Π1 και Π2 που βρίσκονται αντίστοιχα στα σημεία Κ και Λ της επιφάνειας υγρού παράγουν πανομοιότυπα εγκάρσια αρμονικά κύματα με ίδιο πλάτος, ίσες συχνότητες f1 και ίσα μήκη κύματος λ1. Αν η απόσταση των σημείων Κ και Λ είναι d = 2 λ1, τότε δημιουργούνται τέσσερις υπερβολές απόσβεσης, μεταξύ των σημείων Κ και Λ.
Αλλάζοντας την συχνότητα των δύο πηγών σε f2 = 3 f1 και διατηρώντας το ίδιο πλάτος, ο αριθμός των υπερβολών απόσβεσης, που δημιουργούνται μεταξύ των δύο σημείων Κ και Λ, είναι:
i) 6 ii) 8 iii) 12
υ = λ1 f1 = λ2 f2 => λ1 f1 = λ2 3 f1 => λ1 = 3 λ2
υπερβολές απόσβεσης r1 - r2 = N λ2 + λ2/2 = N λ1/3 + λ1/6 r1 + r2 = 2 λ1 2 r1 = N λ1/3 + λ1/6 + 2 λ1 => r1 = N λ1/6 + λ1/12 + λ1
0 < r1 < 2 λ1 => 0 < N λ1/6 + λ1/12 + λ1 < 2 λ1 =>
=> - λ1 < N λ1/6 + λ1/12 + < λ1 =>
=> - 1 - 1/12 < N/6 < 1 - 1/12 => - 13/12 < Ν/6 < 11/12 => - 13/2 < Ν < 11/2
=> Ν = -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5
διακρότημα 2016
Β2. Δύο σύγχρονες πηγές κυμάτων Α και Β δημιουργούν στην επιφάνεια υγρού αρμονικά κύματα ίδιας συχνότητας και ίδιου πλάτους. Σημείο Σ της επιφάνειας του υγρού απέχει από της δύο πηγές αποστάσεις r1 και r2 αντίστοιχα. Αν f1,min η ελάχιστη δυνατή συχνότητα ταλάντωσης των πηγών ώστε τα κύματα να συμβάλλουν ενισχυτικά στο Σ και f2,min η ελάχιστη δυνατή συχνότητα ταλάντωσης των πηγών ώστε τα κύματα να συμβάλλουν αποσβετικά στο Σ, ο λόγος f1,min / f2,min ισούται με :
α) 2 β) 1/2 γ) 1
|r1 - r2| = N λ1 = Ν υ / f1 => f1 = Ν υ /|r1 - r2| για Ν=1 f1,min = υ /|r1 - r2|
|r1 - r2| = N λ2 + λ2 /2 = N υ/f2 + υ/2f2 => f2 = [ N υ + υ/2 ] / |r1 - r2| για Ν=0 f2,min = [ υ/2 ] / |r1 - r2| = υ/2|r1 - r2|
f1,min / f2,min = 2
Β2. Ένα απλό αρμονικό κύμα που διαδίδεται σε ελαστικό μέσο έχει εξίσωση της μορφής
y = Α ημ2π(t/Τ - x/λ). Για να είναι η ταχύτητα διάδοσης του κύματος διπλάσια από τη μέγιστη ταχύτητα ταλάντωσης ενός σημείου του ελαστικού μέσου, θα πρέπει να ισχύει
i. λ = π Α ii. λ = 2π Α iii. λ = 4 π Α.
ταχύτητα κύματος : υ = λ/Τ
y = Α ημ2π(t/Τ - x/λ) => υ = Α 2π/Τ συν2π(t/Τ - x/λ) υμέγιστη = Α 2π/Τ
υ = 2 υμέγιστη => λ/Τ = 2 Α 2π/Τ => λ = 4 π Α
Β2. Σε χορδή που εκτείνεται κατά μήκος του άξονα x ́x, έχει δημιουργηθεί στάσιμο κύμα που προέρχεται από τη συμβολή δύο απλών αρμονικών κυμάτων πλάτους Α, μήκους κύματος λ και περιόδου Τ. Το σημείο Ο, που βρίσκεται στη θέση xo = 0, είναι κοιλία και τη χρονική στιγμή t=0 βρίσκεται στη θέση ισορροπίας του, κινούμενο προς τη θετική κατεύθυνση της απομάκρυνσής του. Το μέτρο της μέγιστης ταχύτητας ταλάντωσης ενός σημείου Μ της χορδής που βρίσκεται στη θέση ΧΜ = 9/8 λ , είναι ίσο με:
i. 2 2½ πΑ/Τ ii. 2πΑ/Τ iii. 4πΑ/Τ .
y = 2A συν(2π x/λ) ημ(2π t/Τ) v = 2A 2π/Τ συν(2π x/λ) συν(2π t/Τ)
x=0, t=0 y = 2A συν0 ημ0 = 0 v = 2A 2π/Τ συν0 συν0 = 2Α 2π/Τ = 4πΑ/Τ > 0
ΧΜ = 9/8 λ v = 4πA/Τ συν(2π 9/8) συν(2 t/Τ) = 4πA/Τ συν(9π/4) συν(2πt/Τ) =
= 4πA/Τ 2½/2 συν(2π t/Τ) = 2 2½ πA/Τ συν(2πt/Τ)
συνεπώς η μέγιστη ταχύτητα ταλάντωσης του σημείου Μ είναι : υΜ,μέγιστη = 2 2½ πA/Τ
Β2. Ένα στάσιμο κύμα που δημιουργείται σε ένα γραμμικό ελαστικό μέσο περιγράφεται από την εξίσωση: Y = 2A συν( 2πx/λ ) ημ( 2πt/T )
Το πλάτος ταλάντωσης Α ́ ενός σημείου Μ του ελαστικού μέσου που βρίσκεται δεξιά του τρίτου δεσμού από το σημείο x = 0 και σε απόσταση λ/12 από αυτόν είναι:
i. A ́ = Α 3½ ii. A ́ = Α/2 iii. A ́ = Α
η ελάχιστη απόσταση δύο δεσμών ή δύο κοιλιών είναι λ/2 κ δ κ δ κ δ
η απόσταση του σημείου Μ από το σημείο x = 0 είναι : ΧΜ = λ + λ/4 + λ/12 = 16λ/12 = 4λ/3
το πλάτος ταλάντωσης του σημείου Μ είναι :
Α' = | 2A συν( 2π 4/3 ) | = |2A συν( 8π/3 )| = |2A συν( 6π/3 + 2π/3 )| = |2A συν( 2π + 2π/3 )| = |2A συν( 2π/3 ) | = | 2Α (-½) | = Α
ΘΕΜΑ Γ
Στην επιφάνεια ενός υγρού που ηρεμεί, βρίσκονται δύο σύγχρονες σημειακές πηγές Π1 και Π2, που δημιουργούν στην επιφάνεια του υγρού εγκάρσια αρμονικά κύματα ίσου πλάτους. Οι πηγές αρχίζουν να ταλαντώνονται τη χρονική στιγμή t0=0 ξεκινώντας από τη θέση ισορροπίας τους και κινούμενες προς την ίδια κατεύθυνση, την οποία θεωρούμε θετική. Η χρονική εξίσωση της ταλάντωσης ενός σημείου Μ,
που βρίσκεται στη μεσοκάθετο του ευθύγραμμου τμήματος Π1Π2, μετά τη συμβολή των κυμάτων δίνεται στο SI από τη σχέση: yM = 0,2 ημ2π(5t-10).
Η ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού είναι υ=2 m/s. Έστω Ο το μέσο του ευθύγραμμου τμήματος Π1Π2 και d=1m η απόσταση μεταξύ των πηγών.
Να βρείτε:
Γ1. Την απόσταση ΜΠ1.
Γ2. Τη διαφορά φάσης των ταλαντώσεων των σημείων Ο και Μ.
Γ3. Πόσα σημεία του ευθύγραμμου τμήματος Π1Π2 ταλαντώνονται με μέγιστο πλάτος.
Γ4. Να σχεδιάσετε τη γραφική παράσταση της απομάκρυνσης του σημείου Μ σε συνάρτηση με τον χρόνο t για 0 ≤ t ≤ 2,5s.
y1 = A ημ(2πt/T - 2πx1/λ) y2 = A ημ(2πt/T - 2πx2/λ)
yM = y1 + y2 = 2A συν(πx2/λ - πx1/λ) ημ( 2πt/T - 2π (x1 + x2) / 2λ )
yM = 0,2 ημ2π(5t-10) => 1/Τ = 5 => Τ = 0,2s λ = υ Τ = 2 0,2 = 0,4 m
(x1 + x2) / 2λ = 10 => (x1 + x2) = 20 λ = 20 v T = 20 2 0,2 = 8m
επειδή το Μ είναι στην μεσοκάθετο x1 = x2 = 4 m
2A = 0,2 m => A = 0,1 m
yO = y1 + y2 = 2A συν(πx2/λ - πx1/λ) ημ( 2πt/T - 2π (x1 + x2) / 2λ ) =
= 2 0,1 συν(0) ημ( 2πt/0,2 - 2π (x1 + x2) / 2λ ) = 0,2 ημ( 10πt - 2π 1 / 2 0,4 ) =
yO = 0,2 ημ2π(5t - 1,25)
φΟ - φΜ = 2π(5t - 1,25) - 2π(5t - 10) = 20π - 2,5π = 17,5π
συν(πx2/λ - πx1/λ) = 1 ή -1 => χ2 - χ1 = Ν λ
χ1 + χ2 = Π1Π2 = 1 m => 2 χ2 = Ν 0,4 + 1 => χ2 = 0,2 Ν + 0,5
πρέπει 0 < χ2 < 1 m =>
=> 0 < 0,2 Ν + 0,5 < 1 m => - 0,5 < 0,2 Ν < 0,5 => - 2,5 < Ν < 2,5 =>
Ν = -2, -1, 0, 1, 2
ΘΕΜΑ 3ο
Σε µια χορδή δηµιουργείται στάσιµο κύµα, με εξίσωση : y = 10 ⋅ συν(πx/4) ⋅ ηµ20πt, όπου x, y δίνονται σε cm και t σε s. Να βρείτε:
α. το µέγιστο πλάτος της ταλάντωσης, τη συχνότητα και το µήκος κύµατος.
β. τις εξισώσεις των δύο κυµάτων που παράγουν το στάσιµο κύµα.
γ. την ταχύτητα που έχει τη χρονική στιγµή t=0,1 s ένα σηµείο της χορδής το οποίο απέχει από το άκρο της x=3 cm.
δ. σε ποιες θέσεις υπάρχουν κοιλίες µεταξύ των σηµείων xΑ=3 cm και xB=9 cm.
y = 2A συν(2πx/λ) ημ(2πt/Τ) = 10 ⋅ συν(πx/4) ⋅ ηµ20πt =>
A = 5 cm 2π/λ = π/4 => λ = 8 cm 2πt/Τ = 20πt => Τ = 0,1 s f = 10 Hz
y1 = 5 ημ(20πt - πx/4) y2 = 5 ημ(20πt + πx/4)
y = 10 ⋅ συν(πx/4) ⋅ ηµ20πt
υ = 10 ⋅ συν(πx/4) ⋅ 20π συν20πt = 200π ⋅ συν(πx/4) ⋅ συν20πt
υ = 200π ⋅ συν(π 3/4) ⋅ συν(20π 0,1) = 200π ⋅ (-0,7) ⋅ συν(2π) = - 140π cm/s
κοιλίες |συν(πx/4)| = 1 => πx/4 = Νπ => x = 4Ν
3 < x < 9 => 3 < 4Ν < 9 => 3/4 < Ν < 9/4 => Ν = 1, 2 υπάρχουν 2 κοιλίες
στις θέσεις x1 = 4N = 4 1 = 4 cm και x2 = 4N = 4 2 = 8 cm
ΘΕΜΑ 3ο 2009
Η εξίσωση ενός γραμμικού αρμονικού κύματος που διαδίδεται κατά μήκος του άξονα x΄x είναι:
y = 0,4ημ2π(2t – 0,5x) (S.I.)
Να βρείτε:
α. Το μήκος κύματος λ και την ταχύτητα διάδοσης του κύματος υ.
β. Τη μέγιστη ταχύτητα ταλάντωσης των σημείων του ελαστικού μέσου.
γ. Τη διαφορά φάσης που παρουσιάζουν την ίδια χρονική στιγμή δύο σημεία του ελαστικού μέσου, τα οποία απέχουν μεταξύ τους απόσταση ίση με 1,5 m.
Για τη χρονική στιγμή t1 = 11/8 s να βρείτε την εξίσωση που περιγράφει το στιγμιότυπο του κύματος, και στη συνέχεια να το σχεδιάσετε.
y(t, x) = 0,4ημ2π(2t – 0,5x) = 2A ημ2π(t/T - x/λ)
A = 0,2 m f = 2 Hz T = 0,5 s λ = 2 m v = 2m 2 Hz = 4 m/s
y(t, x) = 0,4ημ2π(2t – 0,5x) v(t, x) = 1,6π συν2π(2t – 0,5x) υμέγιστη = 1,6π m/s
Δφ / 2π = Δχ / λ => Δφ = 2π 1,5 / 2 = 3π/2 rad
y(11/8, x) = 0,4 ημ2π(2 11/8 – 0,5x) = 0,4 ημ2π(11/4 – 0,5x) = 0,4 ημ(11π/2 – πx)
x = v t = 4 m/s 11/8 s = 11/2 m = 5,5 m

ΘΕΜΑ Γ διακρότημα 2017
Σε ελαστική χορδή ΟΑ μήκους 𝑙 = 0,9𝑚 έχει δημιουργηθεί στάσιμο κύμα με εξίσωση:
y(x,t) = 0,2 συν(2πx/λ) ημ(10πt) (S.I.)
Το σημείο Ο (χ=0) είναι ελεύθερο να κινείται, ενώ το σημείο Α είναι μόνιμα ακίνητο.
Στη χορδή ΟΑ έχουν δημιουργηθεί συνολικά 5 δεσμοί.
Γ1. Να βρεθεί το μέτρο της ταχύτητας του σημείου Μ (𝜒𝛭 = 𝜆/2) τη στιγμή που η απομάκρυνση του από τη θέση ισορροπίας του είναι 𝑦𝛭 = 0,1𝑚.
Γ2. Να σχεδιάσετε το στιγμιότυπο του στάσιμου κύματος στη χορδή ΟΑ τη στιγμή t1 = 1/20 s.
Γ3. Να βρεθεί ο λόγος των ταχυτήτων των σημείων Μ και Κ με 𝜒𝛫 = 𝜆/6.
Γ4. Αλλάζουμε τη συχνότητα ταλάντωσης της χορδής ώστε να σχηματιστεί στάσιμο κύμα με δύο συνολικά δεσμούς . Να γραφεί η εξίσωση απομάκρυνσης σε συνάρτηση με τον χρόνο για το σημείο Μ και να παρασταθεί γραφικά.
y(x,t) = 0,2 συν(2πx/λ) ημ(10πt) = 2A συν(2πx/λ) ημ(2πf t) v(x,t) = 2π συν(2πx/λ) συν(10πt)
A = 0,1 m f = 5 Hz T = 1/f = 0,2 s
5 δεσμοί : Ο(κ) δ δ δ δ Α(δ)
(OA) = l = 4 λ/2 + λ/4 => 0,9m = 9/4 λ => λ = 0,4 m
y(x,t) = 0,2 συν(2πx/0,4) ημ(10πt) => y(x,t) = 0,2 συν(5πx) ημ(10πt)
v(x,t) = 0,2 συν(5πx) 10π συν(10πt) => v(x,t) = 2π συν(5πx) συν(10πt)
xM = λ/2 = 0,4 / 2 = 0,2 m
yΜ (x,t) = 0,2 συν(5πx) ημ(10πt) => 0,1 = 0,2 συν(5π 0,2) ημ(10πt) => ημ(10πt) = - ½
vΜ (x,t) = 2π συν(5πx) συν(10πt) = 2π συν(π) (±Φ3/2) = ± pΦ3 m/s
y(x, 1/20) = 0,2 συν(5πx) ημ(10π /20 ) = 0,2 συν(5πx) 0 < x < 0,9m
vM (λ/2,t) = 2π συν(2π λ/2 / λ) συν(10πt) = 2π συν(π) συν(10πt) = - 2π συν(10πt)
vΚ (λ/6,t) = 2π συν(2π λ/6 / λ) συν(10πt) = 2π συν(π/3) συν(10πt) = π συν(10πt)
vM / vK = - 2
2 δεσμοί : Ο(κ) δ Α(δ)
(OA) = l = λ'/2 + λ'/4 => 0,9m = 3/4 λ' => λ' = 1,2 m
υ = λ f = λ' f ' => 0,4 5 = 1,2 f ' => f ' = 5/3 Hz
yΜ (x,t) = 2A συν(2πx/λ') ημ(2πf ' t) = 0,2 συν(2π 0,2 / 1,2) ημ(2π 5/3 t) =
= 0,2 συν(π/3) ημ(10π/3 t) = 0,2 1/2 ημ(10π/3 t) => yM(0,2 , t) = 0,1 ημ(10π/3 t)
ΘΕΜΑ Δ διακρότημα 2017
Κατά μήκος γραμμικού ελαστικού μέσου που ταυτίζεται με τον άξονα χ’χ διαδίδονται
ταυτόχρονα προς αντίθετες κατευθύνσεις δύο εγκάρσια αρμονικά κύματα ίδιου πλάτους και
ίδιου μήκους κύματος. Από τη συμβολή των δύο αυτών κυμάτων δημιουργείται στο ελαστικό μέσο στάσιμο κύμα με εξίσωση: y = 0,2 συν(5πx) ημ(20πt) (S.I.)
Δ1. Να υπολογίσετε την ταχύτητα διάδοσης των δύο κυμάτων που συμβάλλοντας δημιουργούν το στάσιμο κύμα.
Δ2. Να υπολογίσετε την ενέργεια της ταλάντωσης και να γράψετε την εξίσωση της ταχύτητας ταλάντωσης ενός υλικού σημείου Κ του μέσου, το οποίο βρίσκεται στη θέση χΚ=+0,2m και έχει μάζα m=0,01 Kg.
Δ3. Να υπολογίσετε τη διαφορά φάσης των ταλαντώσεων των σημείων K και Μ του μέσου, αν χΜ=0,4m.
y(x,t) = 0,2 συν(5πx) ημ(20πt) v(x,t) = 4π συν(5πx) συν(20πt)
5π = 2π/λ => λ = 0,4 m 20π = 2πf => f = 10 Hz v = λ f = 0,4 10 = 4 m/s
E = ½ m ω2 Α2 = ½ 0,01 (20π)2 0,22 = ½ 0,01 400 π2 0,04 = 0,08 π2 J
v(xK ,t) = 4π συν(5π 0,2) συν(20πt) = - 4π συν(20πt)
yΜ (x,t) = 0,2 συν(5π 0,4) ημ(20πt) = 0,2 συν(2π) ημ(20πt) = 0,2 ημ(20πt) το Μ είναι κοιλία
yΚ (x,t) = 0,2 συν(5π 0,2) ημ(20πt) = 0,2 συν(π) ημ(20πt) = - 0,2 ημ(20πt) = 0,2 ημ(20πt + π)
τα σημεία Κ και Μ έχουν διαφορά φάσης π rad
ΘΕΜΑ Γ διακρότημα 2016
Σε γραμμικό ελαστικό μέσο διαδίδονται ταυτόχρονα προς αντίθετες κατευθύνσεις δύο εγκάρσια αρμονικά κύματα ίδιου πλάτους, ίδιου μηκους κύματος πουν έχουν ταχύτητα υ = 12 cm/s. Τα δύο κύματα συμβάλλουν οπότε στο ελαστικό μέσο δημιουργείται στάσιμο κύμα με κοιλία στο σημείο Ο, όπου χ(Ο) = 0. Τα ακραία σημεία της ταλάντωσης του σημείου Ο απέχουν μεταξύ τους 20 cm. Σημείο Ζ που βρίσκεται στη θέση χ(Ζ) = 30 cm, είναι δεσμός και μεταξύ του Ο και του Ζ υπάρχουν δύο ακόμη δεσμοί.
Γ1. Γράψτε την εξίσωση του στάσιμου κύματος, αν το Ο τη στιγμή t=0 περνα από τη θέση ισορροπίας με θετική ταχύτητα.
Γ2. Βρείτε την ταχύτητα ταλάντωσης του σημείου Μ ( χΜ = 8 cm ) τη στιγμή t = 2s.
Γ3. Υπολογίστε τον αριθμό των δεσμών που σχηματίζονται ανάμεσα στα σημεία Μ ( χΜ = 8 cm ) και Ν ( χΝ = 48 cm ).
Γ4. Υπολογίστε τη διαφορά φάσης των ταλαντώσεων των υλικών σημείων Μ και Ν.
Γ5. Σχεδιάστε το στιγμιότυπο του στάσιμου κύματος τη στιγμή t = 2,5s από το σημείο Ο ( χ(Ο) = 0 ) έως το σημείο Ζ ( χΖ = 30 cm ).
y(t,x) = 2A συν 2πx/λ ημ 2πt/T (1) 2 2A = 0,2 m => 2A = 0,1 m
O(κ) δ κ δ κ Z(δ)
(ΟΖ) = λ + λ/4 => 0,3 m = 5λ/4 => λ = 0,24 m Τ = λ/υ = 0,24 / 0,12 = 2 s
(1) => y(t,x) = 0,1 συν 2πx/ 0,24 ημ 2πt/2 = 0,1 συν 100πx/12 ημ πt =>
=> y(t,x) = 0,1 συν(25πx/3) ημπt
v(t,x) = 0,1π συν(25πx/3) συνπt
v(0,0) = 0,1π συν(0) συν(0) = 0,1π m/s > 0
v(2, 0,08) = 0,1π συν(25π 0,08/3) συν(π2) = 0,1π συν(2π/3) συν(π2) =
= 0,1π (-½) 1 = - 0,05π m/s
(OM) = 0,08 m = λ/3
(ON) = 0,48 m = 2 λ
(OM) < x < (ON) => λ/3 < N λ/2 + λ/4 < 2λ =>
=> λ/3 - λ/4 < N λ/2 < 2λ - λ/4 =>
=> 1/12 < N/2 < 7/4 =>
=> 1/6 < N < 7/2 => N = 1, 2, 3
N = 1 x = λ/2 + λ/4 = 0,24/2 + 0,24/4 = 0,12 + 0,06 = 0,18 m
N = 2 x = 2 λ/2 + λ/4 = 0,24 + 0,24/4 = 0,24 + 0,06 = 0,3 m
N = 3 x = 3 λ/2 + λ/4 = 3 0,24/2 + 0,24/4 = 0,36 + 0,06 = 0,42 m
y(t, xM ) = 0,1 συν(25π xM /3) ημπt = 0,1 συν(25π 0,08 /3) ημπt = 0,1 συν(2π/3) ημπt = 0,1 (-1/2) ημπt = - 0,05 ημπt
y(t, xN ) = 0,1 συν(25π xN /3) ημπt = 0,1 συν(25π 0,48 /3) ημπt = 0,1 συν(12π/3) ημπt = 0,1 (1) ημπt = + 0,1 ημπt
τα σημεία Μ και Ν έχουν διαφορά φάσης π rad
y(2,5 , x) = 0,1 συν(25πx/3) ημ(π 2,5) = 0,1 συν(25πx/3)
y(2,5 , 0) = 0,1 συν(25π 0/3) ημ(π 2,5) = 0,1 Ο κοιλία
y(2,5 , 0,3) = 0,1 συν(25π 0,3/3) ημ(π 2,5) = 0 Ζ δεσμός
ΘΕΜΑ Γ Ο Ε Φ Ε 2005
Στα σημεία Α και Β της επιφάνειας υγρού που ηρεμεί δημιουργούνται από δύο σύγχρονες πηγές κυμάτων Π1 και Π2 εγκάρσια επιφανειακά κύματα. Η εξίσωση ταλάντωσης της κάθε πηγής είναι : y = 2 ημ5πt ( y σε mm, t σε sec ). Ένα πολύ μικρό κομμάτι φελλού βρίσκεται σε σημείο Σ της επιφάνειας του υγρού σε αποστάσεις r1 = 4 m και r2 αντίστοιχα, από τις πηγές Α και Β. Το κύμα από την πηγή Π1 γθάνει στο Σ τη χρονική στιγμή t1 = 0,4 sec και από την πηγή Π2 με καθυστέρηση Δt = 0,4 sec.
Γ1. Να βρεθούν η ταχύτητα διάδοσης υ και το μήκος κύματος λ των κυμάτων.
Γ2. Να γράψετε την εξίσωση της απομάκρυνσης του φελλού από την θέση ισορροπίας του συναρτήσει του χρόνου.
Γ3. Να βρεθεί η ταχύτητα του φελλού τη στιγμή t3 = 1,2 sec.
Γ4. Να βρεθεί η ελάχιστη συχνότητα ταλάντωσης των πηγών ώστε στο σημείο Σ να επιτυγχάνεαι συμβολή με απόσβεση.
y = 2 ημ5πt ( y σε mm, t σε sec ) Α = 2 mm ω = 2πf = 5π => f = 2,5 Hz T = 1/f = 0,4 s
v = r1 / t1 = 4 m / 0,4 s = 10 m/s r2 = v (t1 + Δt ) = 10 ( 0,4 + 0,4 ) = 8 m
v = λ / Τ => λ = υ Τ = 10 m/s 0,4 s => λ = 4 m
y1 = A ημ(2πft - 2πr1 /λ) = 2 ημ(5πt - 2πr1 /4) => y1 = 2 ημ(5πt - 2π 4 /4) =>
=> y1 = 2 ημ(5πt - 2π)
y2 = 2 ημ(5πt - 2πr2 /4) => y2 = 2 ημ(5πt - 2π 8 /4) => y2 = 2 ημ(5πt - 4π)
y = y1 + y2 = 4 συν π(r2 - r1)/4 ημ [5πt - π(r1 + r2)/4 ] =>
=> y1 + y2 = 4 συν π(8 - 4)/4 ημ [5πt - π(4 + 8)/4 ] =>
=> y1 + y2 = 4 συνπ ημ(5πt - 3π) => y1 + y2 = - 4 ημ(5πt - 3π) συνπ = -1
0 < t < 0,4s yΣ = 0
0,4s < t < 0,8s yΣ = y1 = 2 ημ(5πt - 2π)
0,8s < t yΣ = y1 + y2 = - 4 ημ(5πt - 3π)
t = 1,2 sec yΣ = y1 + y2 = - 4 ημ(5πt - 3π)
υΣ = dyΣ / dt = - 4 5π συν(5πt - 3π) => υΣ = - 20π συν(5πt - 3π)
t = 1,2 sec υΣ = - 20π συν(5π 1,2 - 3π) = - 20π συν(6π - 3π) = 20π mm/s συν3π = -1
στο Σ έχουμε συμβολή απόσβεσης : συν [ 2π(r2 - r1) / 2λ ] = 0 => 2π(r2 - r1) / 2λ = Νπ + π/2
=> ( r2 - r1 )/ λ = Ν + 1/2 => (8 - 4) / λ = Ν + 1/2 => λ = 4 / (Ν + ½) =>
=> υ / f = 4 / (Ν + ½) => 10 / f = 4 / (N + 0,5) => f = 10 (N + 0,5) / 4
N = 0 f = 10 0,5 /4 = 1,25 Hz = fmin
ΘΕΜΑ Δ Ο Ε Φ Ε 2017
Οριζόντια ελαστική χορδή αποτελείται από δύο ομογενή τμήματα (1) και (2), τα οποία έχουν κατασκευασθεί από διαφορετικά υλικά. Το τμήμα (1) εκτείνέται κατά μήκος του θετικού ημιάξονα Oχ, ενώ το τμήμα (2) εκτείνεται κατά μήκος του αρνητικού ημιάξονα Οχ'. Στην αρχή Ο (χ=0) του άξονα χ'Οχ έχει τοποθετηθεί πηγή παραγωγής μηχανικών αρμονικών κυμάτων, η οποία αρχίζει τη χρονική στιγμή t=0 να εκτελεί απλή αρμονική ταλάντωση με εξίσωση της μορφής y = A ημωt. Τα αρμονικά κύματα που παράγονται στην ελαστική χορδή διαδίδονται σε αντίθετες κατευθύνσεις. Τη χρονική στιγμή t1 = 0,35 s το στιγμιότυπο του κύματος στο τμήμα (1) της χορδής είναι της μορφής : y = - 0,05 συν(5πx) 0 < x < 0,7m. Υλικό σημείο Κ ( xK = - 0,15m ) του τμήματος (2) της χορδής έχει εξίσωση απομάκρυνσης από τη θέση ισορροπίας του συναρτήσει του χρόνου, της μορφής : yΚ = 0,05 ημωt t > 0,15 s
Δ1. Γράψτε τις εξισώσεις των παραγομένων κυμάτων.
Δ2. Γράψτε την σχέση της φάσης των ταλαντωσεων των σημείων της χορδής συναρτήσει της τετμημένης χ τη χρονική στιγμή t1.
Δ3. Βρείτε το πλήθος των σημείων της χορδής τα οποία έχουν μέγιστη κινητική ενέργεια και κινούνται προς την ακραία αρνητική θέση της τροχιάς τους τη χρονική στιγμή t2 = 0,4 s.
Δ4. Έστω σημεία Μ, Λ του τμήματος (1) της χορδής, που απέχουν οριζόντια απόσταση ΔχΜΛ = λ1/4 όπου λ1 το μήκος κύματος στο τμήμα (1) της χορδής. Το σημείο Μ ξεκινά την ταλάντωσή του τη στιγμή tΜ και η φάση της ταλάντωσής του κάθε χρονική στιγμή είναι συνεχώς μεγαλύτερη από τη φάση της ταλάντωσής του σημείου Λ. Υπολογίστε την απομάκρυνση από τη θέση ισορροπίας του σημείου Λ τη χρονική στιγμή t3 = tΜ + Τ/3.
Δ1. y = A ημ(2πft - 2πx/λ) x > 0 y = A ημ(2πft + 2πx/λ) x < 0
το στιγμιότυπο του κύματος y = - 0,05 συν(5πx) 0 < x < 0,7m τη στιγμή t1 = 0,35 s τότε Α = 0,05 m και 2πx/λ = 5πx => λ = 0,4 m = λ1
η ταχύτητα του κύματος όταν χ>0 είναι υ1 = 0,7m / 0,35 s = 2 m/s
η συχνότητα παραγωγής ηχητικών υμάτων της πηγής είναι : f = v1 / λ = 2m/s / 0,4m = 5 Hz
yK = 0,05 ημ2πft t > 0,15 s το κύμα φθάνει στο σημείο Κ ( xK = - 0,15m ) σε χρόνο 0,15s
η ταχύτητα του κύματος όταν χ<0 είναι υ2 = 0,15 m / 0,15 s = 1 m/s
το μήκος κύματος του κύματος που διαδίδεται στο τμήμα (2) της χορδής είναι :
λ2 = v2 / f = 1m/s / 5Hz = 0,2 m
y = A ημ(2πft - 2πx/λ) x > 0
y = 0,05 ημ(2π 5 t - 2πx/ 0,4) => y = 0,05 ημ(10πt - 5πx) x > 0
y = A ημ(2πft + 2πx/λ) x < 0
y = 0,05 ημ(2π 5 t + 2πx/ 0,2) => y = 0,05 ημ(10πt + 10πx) x < 0
Δ2.
φ1 = 10πt - 5πx = 10π 0,35 - 5πx = 3,5π - 5πx x > 0 φ1 = 0 => x = 0,7 m
φ2 = 10πt + 10πx = 10π 0,35 + 10πx = 3,5π + 10πx x > 0 φ2 = 0 => x = 0,35 m
φ1 = 3,5π - 5πx 0 < x < 0,7 m
φ2 = 3,5π + 10πx - 0,35 m < x < 0
Δ3. t = 0,4 s x1 = v1 t = 2m/s 0,4s = 0,8 m x2 = v2 t = 1m/s 0,4s = 0,4 m
y = 0,05 ημ(10πt - 5πx) = 0,05 ημ(10π 0,4 - 5πx) = - 0,05 ημ(5πx - 4π) 0 < x < 0,8 m
v = 0,05 10π συν(10π 0,4 - 5πx) = 0,5π συν(4π - 5πx)
μέγιστη κινητική ενέργεια είναι όταν y = 0 => ημ(5πx - 4π) = 0 => 5πx - 4π = Νπ =>
=> x = Ν/5 + 4/5
0 < x < 0,8 m => 0 < Ν/5 + 4/5 < 0,8 m => - 0,8 < Ν/5 < 0 => - 4 < Ν < 0
Ν = -4, -3, -2, -1, 0
Ν = -4 x = -4/5 + 4/5 = 0 v = 0,5π συν(4π - 5πx) = 0,5π συν(4π) = 0,5π m/s > 0
N = -3 x = -3/4 + 4/5 = 0,2 m
v = 0,5π συν(4π - 5πx) = 0,5π συν(4π - 5π 0,2) = 0,5π συν(4π - π) = - 0,5π m/s < 0
N = -2 x = -2/5 + 4/5 = 0,4 m
v = 0,5π συν(4π - 5πx) = 0,5π συν(4π - 5π 0,4) = 0,5π συν(4π - 2π) = 0,5π m/s > 0
N = -1 x = -1/5 + 4/5 = 0,6 m
v = 0,5π συν(4π - 5πx) = 0,5π συν(4π - 5π 0,6) = 0,5π συν(4π - 3π) = - 0,5π m/s < 0
N = 0 x = 0,8 m
v = 0,5π συν(4π - 5πx) = 0,5π συν(4π - 5π 0,8) = 0,5π συν(4π - 4π) = 0,5π m/s > 0
δηλαδή στα σημεία x = +0,2 m , +0,6 m τα υλικά σημεία διέρχονται από τη θέση ιασορροπίας τους και η ταχύτητα είναι αρνητική
y = 0,05 ημ(10πt + 10πx) - 0,4 m < x < 0
y = 0,05 ημ(10πt + 10πx) = 0,05 ημ(10π 0,4 + 10πx) = 0,05 ημ(10πx + 4π) - 0,4 m < x < 0
v = 0,05 10π συν(10π 0,4 + 10πx) = 0,5π συν(4π + 10πx)
μέγιστη κινητική ενέργεια είναι όταν y = 0 => ημ(10πx + 4π) = 0 => 10πx + 4π = Νπ =>
=> x = Ν/10 - 4/10
- 0,4 m < x < 0 => - 0,4 m < Ν/10 - 4/10 < 0 => 0 < Ν/10 < 0,4 => 0 < Ν < 4
οπότε : Ν = 0, 1, 2, 3, 4
Ν = 0 x = - 0,4 m v = 0,5π συν(4π + 10πx) = 0,5π συν(0) = 0,5π m/s > 0
N = 1 x = 1/10 - 4/10 = - 0,3 m v = 0,5π συν(4π + 10πx) = 0,5π συν(4π + 10π (-0,3)) = 0,5π συν(4π - 3π) = 0,5π συν(π) = - 0,5π m/s < 0
N = 2 x = 2/10 - 4/10 = - 0,2 m v = 0,5π συν(4π + 10πx) = 0,5π συν(4π + 10π (-0,2)) = 0,5π συν(4π - 2π) = 0,5π συν(2π) = 0,5π m/s > 0
N = 3 x = 3/10 - 4/10 = - 0,1 m v = 0,5π συν(4π + 10πx) = 0,5π συν(4π + 10π (-0,1)) = 0,5π συν(4π - π) = 0,5π συν(3π) = - 0,5π m/s < 0
N = 4 x = 4/10 - 4/10 = 0 v = 0,5π συν(4π + 10πx) = 0,5π συν(4π) = 0,5π m/s > 0
δηλαδή στα σημεία x = - 0,3 m , - 0,1 m τα υλικά σημεία διέρχονται από τη θέση ιασορροπίας τους και η ταχύτητα είναι αρνητική
Δ4. tM = xM / v1 = xM / 2 T = 1/f = 1/5 = 0,2 sec
φΜ = 10πt - 5πxΜ > φΛ = 10πt - 5πxΛ => xΛ > xM
xΛ - xM = λ1 / 4 = 0,1 m => φΜ - φΛ = π/2 rad
yΛ = 0,05 ημ(10πt - 5πxΛ ) = 0,05 ημ(10π (tM + T/3) - 5πxΛ ) =
= 0,05 ημ(10π (xM /2 + 0,2/3) - 5πxΛ ) =
= 0,05 ημ(5πxM + 2π/3 - 5πxΛ ) = 0,05 ημ(5π (xM - xΛ) + 2π/3 ) =
= 0,05 ημ( -0,5π + 2π/3 ) = 0,05 ημ( -0,5π) συν( 2π/3 ) =
= - 0,05 (-1/2) = + 0,025 m
.......................................................................................................................................
Δύο σύγχρονες πηγές κυμάτων Π1 και Π2 δημιουργούν στην επιφάνεια υγρού που ηρεμεί εγκάρσια κύματα που διαδίδονται με ταχύτητα μέτρου υ = 80 cm/s. Οι δύο πηγές τη χρονική στιγμή t = 0 αρχίζουν να εκτελούν απλή αρμονική ταλάντωση, σε διεύθυνση κέθετη στην επιφάνεια του υγρού με εξίσωση ταλάντωσης : y = Α ημ(2πt/Τ). Μικρό κομμάτι φελλού βρίσκεται στην επιφάνεια του υγρού και με την επίδραση των δύο κυμάτων ταλαντώνεται με εξίσωση απομάκρυνσης από τη θέση ισορροπίας του : y = 4 ημ2π(8t - 4) όπου y σε cm και t σε sec. Οι αποστάσεις του φελλού από τις πηγές Π1 και Π2 είναι αντίστοιχα : r1 και r2 και συνδέονται με την σχέση : r1 - r2 = 2λ όπου λ το μήκος κύματος των δύο κυμάτων.
Α) Γράψτε τις εξισώσεις των δύο κυμάτων
Β) Υπολογίστε την ταχύτητα και την επιτάχυνση του φελλού την στιγμή t = 1s.
Γ) Υπολογίστε την χρονική στιγμή t κατά την οποίαν ο φελλός περνά από τη θέση :
Γ1) μέγιστης απομάκρυνσης y = +4 cm για 1η φορά εκτελώντας σύνθετη ταλάντωση.
Γ2) μέγιστης απομάκρυνσης y = -4 cm για 1η φορά εκτελώντας σύνθετη ταλάντωση.
Δ) Σημείο Σ της μεσοκαθέτου του ευθυγράμμου τμήματος που συνδέει τις δύο πηγές ταλαντώνεται λόγω των δύο κυμάτων που φθάνουν σ'αυτό. Γράψτε την εξίσωση της επιτάχυνσης ταλάντωσης του σημείου Σ συναρτήσει του χρόνου.
A) y1 = Α ημ2π(t/Τ - r1 /λ) y2 = Α ημ2π(t/Τ - r2 /λ)
y = y1 + y2 = 2Α συν2π(r1 - r2)/2λ ημ2π(t/Τ - (r1 + r2)/2λ)
y = 4 ημ2π(8t - 4) όπου y σε cm t σε sec v = 80 cm/s = λ f r1 - r2 = 2λ
συμπεραίνουμε ότι : 2Α συν2π(r1 - r2)/2λ = 4 cm => 2Α συν2π = 4 cm => Α = 2 cm
f = 8 Hz T = 1/f = 1/8 s λ = v/f = 10 cm = 0,1 m άρα r1 - r2 = 2λ = 0,2 m
και (r1 + r2)/2λ = 4 => r1 + r2 = 80 cm = 0,8 m
συνεπώς : r1 = 0,5 m και r2 = 0,3 m οι αποστάσεις του φελλού από τις πηγές Π1 και Π2
άρα έχουμε : y1 = Α ημ2π(t/Τ - r1 /λ) = 0,02 ημ2π(8t - 0,5/0,1) => y1 = 0,02 ημ2π(8t - 5)
και y2 = Α ημ2π(t/Τ - r2 /λ) = 0,02 ημ2π(8t - 0,3/0,1) => y2 = 0,02 ημ2π(8t - 3)
B) y = 4 ημ2π(8t - 4) ( cm ) υ = dy/t = 4 16π συν2π(8t - 4) = 64π συν2π(8t - 4) ( cm/s )
a = dv/dt = - 64π 16π ημ2π(8t - 4) => a = - 1024π2 ημ2π(8t - 4) ( cm/s2 )
t = 1 sec a = - 1024π2 ημ2π(8 - 4) = - 1024π2 ημ8π = 0
v = 64π συν2π(8 - 4) = 64π συν8π = 64π cm/s
Γ)
από την πηγή Π1 το κύμα φθάνει στον φελλό σε χρόνο t1 = r1 / v = 0,5 m / 0,8 m/s = 5/8 s = 20/32 s
από την πηγή Π2 το κύμα φθάνει στον φελλό σε χρόνο t2 = r2 / v = 0,3 m / 0,8 m/s = 3/8 s = 12/32 s
y = + 4 cm =>
=> 4 ημ2π(8t - 4) = +4 => ημ2π(8t - 4) = 1 = ημπ/2 => 2π(8t - 4) = 2Nπ + π/2 =>
=> 8t - 4 = N + 1/4 => t = N/8 + (1/4 + 4)/8 => t = N/8 + 17/32 ( sec )
N = 0 t = 17/32 s ο φελλός ταλαντώνεται λόγω του κύματος από την πηγή Π2
Ν = 1 t = 1/8 + 17/32 s = 21/32 s στον φελλό έχουν φθάσει και τα δύο κύματα ο φελλός βρίσκεται σε μέγιστη απομάκρυνση y = + 4 cm για 1η φορά
y = - 4 cm =>
=> 4 ημ2π(8t - 4) = - 4 => ημ2π(8t - 4) = - 1 = ημ3π/2 => 2π(8t - 4) = 2Nπ + 3π/2 =>
=> 8t - 4 = N + 3/4 => t = N/8 + (3/4 + 4)/8 => t = N/8 + 19/32 ( sec )
N = 0 t = 19/32 s ο φελλός ταλαντώνεται λόγω του κύματος από την πηγή Π2
Ν = 1 t = 1/8 + 19/32 s = 23/32 s στον φελλό έχουν φθάσει και τα δύο κύματα ο φελλός βρίσκεται σε μέγιστη απομάκρυνση y = - 4 cm για 1η φορά
Δ) σημείο Σ βρίσκεται στη μεσοκάθετο του ευθυγράμμου τμήματος που συνδέει τις δύο πηγές και απέχει r1 = r2 = r από αυτές
y(Σ) = y1 + y2 = 2Α συν2π(r1 - r2)/2λ ημ2π(t/Τ - (r1 + r2)/2λ) =
= 2Α συν0 ημ2π(t/Τ - (r + r)/2λ) = 2Α ημ2π(t/Τ - r/λ) =>
=> y(Σ) = 0,04 ημ2π(8t - r/0,1) => y(Σ) = 0,04 ημ2π(8t - 10r) (S.I.)
υ(Σ) = 0,04 16π συν2π(8t - 10r) => υ(Σ) = 0,64π συν2π(8t - 10r) (S.I.)
α(Σ) = - 0,64π 16π ημ2π(8t - 10r) => α(Σ) = - 10,24 π2 ημ2π(8t - 10r) (S.I.)
....................................................................................................................
Τεντωμένη χορδή ΑΒ με μήκος 4,5 m έχει το άκρο Β ακλόνητα στερεωμένο και το Α ελεύθερο. Τη στιγμή t = 0 το άκρο Α που βρίσκεται στη θέση x = 0 αρχίζει να ταλαντώνεται χωρίς αρχική φάση κάθετα στη διεύθυνση της χορδής δημιουργώντας εγκάρσιο αρμονικό κύμα που διαδίδεται με ταχύτητα υ = 2 m/s. Τη στιγμή t1 = 2 s σημείο Δ της χορδής που είναι στη θέση xΔ = 1 m έχει φάση φ = 3π rad και ταχύτητα ταλάντωσης με μέτρο 0,05π m/s.
Γράψτε την εξίσωση της απομάκρυνσης του σημείου Δ συναρτήσει του χρόνου.
A) y1 = Α ημ2π(t/Τ - x/λ) τρέχον κύμα y2 = Α ημ2π(t/Τ + x/λ) ανακλώμενο κύμα
t = (AB) / v = 4,5 m / 2 m/s = 2,25 s λ = υ Τ = 2 m/s Τ
τη στιγμή t = 2 s στη χορδή διαδίδεται το τρέχον κύμα ( δεν έχει ανακλασθεί ) οπότε η φάση του σημείου Δ είναι φ = 2π(t/Τ - x/λ) => 3π = 2π(2/Τ - 1/(2Τ)) => 3/2 = 4/(2Τ) - 1/(2Τ) => Τ=1s
λ = υ Τ = 2 m/s 1 s = 2 m
Ν λ/2 + λ/4 = (ΑΒ) = 4,5 m => Ν 2/2 + 2/4 = 4,5 m => N = 4 άτρακτοι ( 4 κοιλίες )
yΔ = Α ημ2π(t/Τ - x/λ)
υΔ = Α 2π/Τ συν2π(t/Τ - x/λ) => 0,05π = Α 2π συν2π(2/1 - 1/2) =>
=> 0,05 = 2Α συν3π => 0,05 = 2Α (-1) => Α = 0,025 m η ταχύτητα του σημείου Δ είναι αρνητική υΔ = - 0,05π m/s
το κύμα φθάνει στο σημείο Δ σε χρόνο t = xΔ / v = 1m / 2m/s = 0,5 s
τη στιγμή t = 2s το σημείο Δ διέρχεται από τη θέση ισορροπίας του με κατεύθυνση προς τα κάτω
συνεπώς yΔ = Α ημ2π(t/Τ - x/λ) = 0,025 ημ2π(t/1 - 1/2) => yΔ(t) = 0,025 ημ(2πt - π)
ταχύτητα : υΔ(t) = 0,05π συν(2πt - π)
επιτάχυνση : aΔ(t) = - 0,1π2 ημ(2πt - π) 0,5 s < t < 2,25 s
το τρέχον κύμα στη χορδή έχει εξίσωση :
y = Α ημ2π(t/Τ - x/λ) = 0,025 ημ2π(t/1 - x/2) = 0,025 ημ(2πt - πx)
όταν ανακλασθεί το τρέχον κύμα στο ακλόνητο σημείο Β υφίσταται διαφορά φάσης π rad και κινείται προς την αντίθετη κατεύθυνση
το ανακλώμενο κύμα θα έχει εξίσωση y2 = Α ημ2π(t/Τ + x/λ + π) = 0,025 ημ2π(t + x/2 + π)
η σύνθεση των δύο κυμάτων έχει αποτέλεσμα στάσιμο κύμα με εξίσωση :
y = y1 + y2 = 0,025 ημ(2πt - πx) + 0,025 ημ(2πt + πx + π) =
= 0,05 ημ(2πt - πx + 2πt + πx + π)/2 συν(2πt - πx - 2πt - πx - π)/2 =
= 0,05 ημ(2πt + π/2) συν( - 2πx - π/2) = 0,05 ημ(2πt + π/2) συν(2πx + π/2) =
= 0,05 συν(2πt) [ - ημ(2πx) ] => y(t, x) = - 0,05 ημ(2πx) συν(2πt)
θεωρώντας το άκρο Β (δεσμός) ως x = 0 το σμείο Δ έχει απομάκρυνση από τη θέση ισορροπίας του yΔ (t, x) = - 0,05 ημ(2πxΔ ) συν(2πt) = - 0,05 ημ(2π 3,5) συν(2πt) = 0 είναι
y = 2A συν(2πx/λ) ημ(2πt/Τ) v = 2A 2π/Τ συν(2πx/λ) συν(2πt/Τ)
0,05π = 2A 2π 3/4 συν(2π1/2) συν(3π) => 0,05 = - 3A συν(π)









