ΘΕΜΑ Γ  διακρότημα 2018
Η ηχητική πηγή S είναι ακίνητη σε απόσταση L=50m από κατακόρυφη ανακλαστική επιφάνεια. Παρατηρητής Α βρίσκεται σε απόσταση d=250m από την ηχητική πηγή  και 300m από την κατακόρυφη επιφάνεια  στην ίδια ευθεία.  Τη t=0  ο παρατηρητής Α έχει ταχύτητα 𝜐_𝐴 = 10𝑚/𝑠  πλησιάζοντας την πηγή και εκείνη τη στιγμή η ηχητική πηγή αρχίζει να εκπέμπει ήχο συχνότητας 𝑓_𝑆 = 680𝐻𝑧. 

Γ1. Να βρεθεί το μήκος κύματος των ηχητικών κυμάτων που παράγει η πηγή και η συχνότητα του ήχου που καταγράφει ο παρατηρητής απ’ ευθείας από την πηγή.
Γ2. Να βρεθεί ποια χρονική στιγμή t₁ ο παρατηρητής αρχίζει να αντιλαμβάνεται τον ήχο που έρχεται απευθείας από την ηχητική πηγή και ποια χρονική στιγμή t₂ φθάνει σε αυτόν ο ήχος μετά την ανάκλαση του στην ανακλαστική επιφάνεια.
Γ3. Να βρεθεί η συχνότητα που αντιλαμβάνεται ο παρατηρητής απευθείας από την πηγή αμέσως μετά την μετωπική και ελαστική σύγκρουση του με αυτή, αν για τις μάζες τους ισχύει 𝑚_𝐴 = 𝑚_𝑆/3 .
Γ4. Να βρεθεί το μήκος κύματος των ηχητικών κυμάτων που καταγράφει ο παρατηρητής αμέσως μετά την κρούση, απευθείας από την ηχητική πηγή.

Το επίπεδο στο οποίο κινούνται η πηγή και ο παρατηρητής είναι λείο. Η ταχύτητα του ήχου στον αέρα είναι 𝜐_𝜂𝜒 = 340 𝑚/𝑠.

    υ_ηχ = λ 𝑓_𝑆   =>   λ = 340 / 680 =  0,5 m  

  f_A  =  f_S  ( υ_ηχ + v_A ) / υ_ηχ  =  680  ( 340 + 10 ) / 340  =  2 350  =>   f_A = 700 Hz 

   t₁ υ_ηχ  +  t₁ v_A  =  d  =>  t₁ ( 340 + 10 ) =  250  =>   t₁  =  250 / 350 = 5/7 sec  

                   L = t' υ_ηχ  =>  t' = 50 / 340 s        x_A' = t' v_A  =  5/34  10  =  50/34 m  

          t" v_A  +  t" υ_ηχ  =  L  +  d  -  x_A'  =>  t" 10  +  t" 340  =  50  +  250 -  50/34  =>  

                  =>   t" 350  =  300 -  50/34  =>  t"  =  300/350  -  1/(7*34)  =  6/7  -  1/(7*34)

       t₂  =  t'  +  t"  =  5/34  + 6/7  -  1/(7*34)  =  ( 35  +  6*34  -  1 ) / (7*34)  =  238 / 238 = 1 s

   t₂ υ_ηχ  +  t₂ v_A  =  d  + L +  L  =>   t₂ 340  +  t₂ 10  =  350  =>  t₂  =  350 / 350 = 1 s  

  ελαστική κρούση 

  v_A'  =  v_A ( m_A - m_S ) / ( m_A + m_S )  =  10  ( m_A - 3 m_A ) / ( m_A + 3 m_A ) = 10 ( - 1/2 ) = - 5 m/s

  v_S'  = 2 m_A v_A / ( m_A + m_S )  =  2 m_A 10 / ( m_A + 3 m_A ) = +5 m/s    

  f_A' =  f_{S *} ( υ_ηχ + v_A' ) / ( υ_ηχ + v_S' )  =  680 _* ( 340 - 5 ) / ( 340 + 5 ) =  680 _* 335 / 345 =>

    =>     f_A' =  67/69 _* 680 Ηz

ο Α απομακρύνεται από την πηγή  άρα  η ταχύτητα του ήχου ως προς τον παρατηρητή = υ_ηχ - v_A = 340 - 5      οπότε  αντιλαμβάνεται  συχνότητα  f_A  και μήκος κύματος  λ_Α :    f_A = ( υ_ηχ - v_A ) / λ_A    

 η πηγή απομακρύνεται από τον Α     το μήκος κύματος που αντιλαμβάνεται ο Α είναι η απόσταση δύο διαδοχικών μεγίστων που εκπέμπει η πηγή,  τη στιγμή t  η πηγή εκπέμπει ένα μέγιστο  και τη στιγμή t + Τ εκπέμει το επόμενο μέγιστο ( Τ = 1/ f_S )  εντωμεταξύ η πηγή έχει απομακρυνθεί σε χρόνο Τ απόσταση  v_S T   άρα το μήκος κύματος που αντιλαμβάνεται ο παρατηρητής Α  ισούται με το μήκος κύματος που εκπέμπει η πηγή  αν ήταν ακίνητη  +  την απόσταση που η πηγή διανύει σε χρόνο Τ   

  λ_Α  =  λ +  v_S T =  υ_ηχ / f_S  +  v_S / f_S  =>   λ_Α = ( υ_ηχ + v_S ) / f_S  = ( 340 +  5 ) / 680  =  0,50735 m   

    συνολικά έχουμε :    f_A  =  ( υ_ηχ - v_A ) / λ_A  =   f_S * ( υ_ηχ - v_A ) / ( υ_ηχ + v_S )

ο αέρας είναι ακίνητος οπότε τα ηχητικά κύματα που εκπέμπει η πηγή διαδίδονται με ταχύτητα   υ_ηχ = λ f_S 

ΘΕΜΑ Γ    fysicasta

Περιπολικό ξεκινά να κινείται τη χρονική στιγμή t=0 από την ηρεμία και η ταχύτητα του αυξάνεται με
σταθερό ρυθμό 2m/s² και ταυτόχρονα ενεργοποιεί την σειρήνα του, η οποία εκπέμπει ήχο συχνότητας 990Ηz.  Στην διεύθυνση κίνησης του περιπολικού και σε απόσταση d=1045m από το σημείο που ξεκίνησε βρίσκεται ακίνητος παρατηρητής Α.        Να υπολογιστούν:
α)   η συχνότητα με την οποία αντιλαμβάνεται ο παρατηρητής τον ήχο που εξέπεμψε η σειρήνα τη
χρονική στιγμή t1=8s.
  **    η συχνότητα του ήχου που φτάνει στον παρατηρητή τη χρονική στιγμή t1=8s. 
β)   Τη χρονική στιγμή t1=8s το περιπολικό μηδενίζει ακαριαία την επιτάχυνσή του και αρχίζει να
κινείται με σταθερή ταχύτητα.   Πόσο είναι το μήκος κύματος του ήχου που αντιλαμβάνεται ο
παρατηρητής τις χρονικές στιγμές t2=42s και t3=100s.
γ)   Πόσους παλμούς κατέγραψε ο παρατηρητής από της τη χρονική στιγμή t1=8s έως t2=42s;
Η ταχύτητα του ήχου ας θεωρηθεί ως 340 m/s.   Δίνεται   330² = 108900

  α)    v_s  =  a t  =>  v_s  =  2t    ταχύτητα περιπολικού συναρτήσει του χρόνου

  x  =  0,5  a  t²  =  0,5  2  t²  =  t²                   t = 8s     v_s = 16 m/s      x = 64 m

 η πηγή πλησιάζει τον ακίνητο παρατηρητή   f_A  =  f_s  v_ηχ / ( υ_ηχ - 2t )  =>  f_A(t)  =  990  340 / ( 340 - 2t ) 

       t = 8s       f_A(8)  =  990  340 / ( 340 - 16 )  =  990  340 / 324 Hz  =  1038,9 Hz     

**  τη στιγμή  t = 0  ξεκινά το περιπολικό με επιτάχυνση  α = 2m/s²,  έστω μετά από χρόνο  t  εκπέμπει ήχο  ο οποίος φθάνει στον παρατηρητή Α  τη στιγμή  t = 8s,   το περιπολικό σε χρόνο  t  έχει αποκτήσει ταχύτητα  v_s  =  a t  =  2t    και  έχει διανύσει διάστημα  x  =  0,5  a  t²  =  0,5  2  t²  =  t² ,    ο ήχος  κινείται με σταθερή ταχύτητα  υ_ηχ = 340 m/s  διανύοντας απόσταση  340 ( 8 - t ) ,   συνολικά έχουμε   t²  +  340 ( 8 - t ) = 1045 m   =>   t²  -  340 t  +  2720  =  1045  =>     t²  -  340 t  +  1675 =  0           Δ  =  340²  -  4 1675  =  115600  -  6700  =  108900  =  330²    

       t  = { - ( -340 ) ±  330 }  /  2  =  { 340  ±  330 }  /  2  =  335 s   απορρίπτεται    ή    5 s    δεκτή λύση     

   το περιπολικό σε  5 s  έχει αποκτήσει ταχύτητα  v_s  =  a t  =  2 m/s²  5 s  =  10 m/s   

η πηγή πλησιάζει τον ακίνητο παρατηρητή   f_A  =  f_s  v_ηχ / ( υ_ηχ - v_s ) =  990  340 / ( 340 - 10 ) =>  f_A  = 1020 Hz

β)   v_s  =  16 m/s       x  =  64m  +  16m/s  ( 42s - 8s )  =  64m  +  544m  =  608m   <  1045m   η πηγή πλησιάζει τον Α

     λ_Α  =  λ  -  v_s Τ  =  λ  -  v_s / f_s  =  υ_ηχ / f_s  -  v_s / f_s  =  ( 340 - 16 ) / 990  =  0,327 m 

   v_s  =  16 m/s       x  =  64m  +  16m/s  ( 100s - 8s )  =  64m  +  1472m  =  1536m   >  1045m  η πηγή έχει προσπεράσει τον Α  και  απομακρύνεται απ' αυτόν

     λ_Α  =  λ  +  v_s Τ  =  λ  +  v_s / f_s  =  υ_ηχ / f_s  +  v_s / f_s  =  ( 340 + 16 ) / 990  =  0,360 m 

γ)  από  t₁ = 8s  έως  t₂ = 42s  ο παρατηρητής κατέγραψε  Ν = f_A (t₂ - t₁) = 1038,9 Hz ( 42s - 8s ) = 35322 παλμούς

Γ1.  Η ηχητική πηγή κινείται με σταθερή ταχύτητα υs=34m/s και εκπέμπει ήχο συχνότητας fs=1000Ηz για χρονικό διάστημα Δt=10s.  Να υπολογιστούν:              Α              S  ^υs®            B
α)   Οι συχνότητες που ακούνε οι δύο ακίνητοι παρατηρητές, Α και Β.
β)   Τα μήκη κύματος που καταγράφουν για τον ήχο.
γ)   Οι χρονικές διάρκειες που ακούνε τον ήχο.
δ)   Αν οι Α και Β έμπαιναν σε κίνηση η Α προς τα δεξιά και ο Β προς αριστερά με τις ίδιες κατά
μέτρο ταχύτητες υΑ=υΒ=34m/s, ποιες αλλαγές θα υπήρχαν στα αποτελέσματα των τριών
προηγούμενων ερωτήσεων;
Δίνεται η ταχύτητα του ήχου στον αέρα υ=340m/s.

 α)   f_A  =  f_S  v / (v + v_S)  =  1000  340 / (340 + 34)  =  1000  340 / ( 11 34 )  =  10000/11 Hz

       f_B  =  f_S  v / (v - v_S)  =  1000  340 / (340 - 34)  =  1000  340 / ( 9 34 )  =  10000/9 Hz

β)

 λ_Α  =  λ  +  v_S Τ  =  υ Τ  +  v_S Τ  =  ( υ + v_S ) Τ   =  ( υ + v_S ) 1/f_S  = ( υ + v_S ) / f_S  = ( 340 + 34 ) / 1000  = 0,374 m

 λ_B  =  λ - v_S Τ  =  υ Τ  -  v_S Τ  =  ( υ  -  v_S ) Τ   =   ( υ - v_S ) 1/f_S   =  ( υ - v_S ) / f_S  = ( 340 - 34 ) / 1000 = 0,306 m

γ) η πηγή εκπέμπει 1000 παλμούς ανά δευτερόλεπτο   άρα  σε 10s  εκπέμπει Ν  =  f_S  Δt  =  1000  10  =  10⁴ παλμούς

ο ακίνητος παρατηρητής Α  ακούει τους Ν παλμούς   Ν  =  f_A  t_A  =>   10⁴  =  10000/11  t_A  =>  t_A  =  11s 

ο ακίνητος παρατηρητής B  ακούει τους Ν παλμούς   Ν  =  f_B  t_B  =>   10⁴  =  10000/9 t_B  =>  t_B  =  9s 

δ)     

   f_A  =  f_S  (v - υ_Α) / (v + v_S)  =  1000  (340 - 34) / (340 + 34)  =  1000  (9 34) / ( 11 34 )  =  9/11 10³ Hz

   f_B  =  f_S  (v + υ_Β) / (v - v_S)  =  1000  (340 + 3) / (340 - 34)  =  1000  (11 34) / ( 9 34 )  =  11/9 10³ Hz

η ταχύτητα του ήχου ως προς τον Α είναι :   v - υ_Α =  340 - 34 = 306 m/s      

το μήκος κύματος που αντιλαμβάνεται ο Α είναι :  λ_Α = ( v - υ_Α ) / f_A  =   9 34  11/9  10^-3  =  11 34 / 1000 = 0,374 m

 λ_Α  =  λ  +  v_S Τ  =  υ Τ  +  v_S Τ  =  ( υ + v_S ) Τ   =  ( υ + v_S ) 1/f_S  = ( υ + v_S ) / f_S  = ( 340 + 34 ) / 1000  = 0,374 m

η ταχύτητα του ήχου ως προς τον B είναι :   v + υ_B =  340 + 34 = 374 m/s

το μήκος κύματος που αντιλαμβάνεται ο Β είναι :  λ_Β = ( v + υ_Β ) / f_Β  =   11 34  9/11  10^-3  =  9 34 / 1000 = 0,306 m

 λ_B  =  λ - v_S Τ  =  υ Τ  -  v_S Τ  =  ( υ  -  v_S ) Τ   =   ( υ - v_S ) 1/f_S   =  ( υ - v_S ) / f_S  = ( 340 - 34 ) / 1000 = 0,306 m

η πηγή εκπέμπει 1000 παλμούς ανά δευτερόλεπτο   άρα  σε 10s  εκπέμπει Ν  =  f_S  Δt  =  1000  10  =  10⁴ παλμούς

ο ακίνητος παρατηρητής Α  ακούει τους Ν παλμούς   Ν  =  f_A  t_A  =>   10⁴  =  9/11 10³  t_A   =>  t_A  =  110/9 s 

ο ακίνητος παρατηρητής B  ακούει τους Ν παλμούς   Ν  =  f_B  t_B  =>   10⁴  =  11/9 10³  t_B   =>  t_B  =  90/11 s 

Γ2.    Το ελατήριο του σχήματος έχει σταθερά k=400Ν/m και έχει στο ένα άκρο του στερεωμένο ένα σώμα, Σ1, μάζας m₁=1kg που φέρει ενσωματωμένο  δέκτη ήχου, Δ. Το σύστημα εκτελεί απλή αρμονική ταλάντωση πλάτους 0,4m πάνω σε λείο οριζόντιο επίπεδο. Τη στιγμή που το σώμα Σ1  διέρχεται από τη θέση ισορροπίας του, συγκρούεται κεντρικά ελαστικά με ακίνητο σώμα Σ2,   μάζας m₂=3kg, το οποίο φέρει ενσωματωμένη πηγή ήχου συχνότητας f_s=688Ηz.
Να βρείτε:
α)  την ταχύτητα του σώματος Σ1 ελάχιστα πριν τη σύγκρουση.
β)  τις ταχύτητες των σωμάτων Σ1 και Σ2 αμέσως μετά τη σύγκρουση καθώς και το πλάτος της νέας ταλάντωσης.
γ)  τη συχνότητα που ανιχνεύει ο δέκτης όταν το σώμα Σ1 διέρχεται για 1η και για 2η φορά μετά την κρούση από την απομάκρυνση x1= - 0,1 3^1/2 m . Να θεωρήσετε θετικό τον ημιάξονα προς τα δεξιά.
δ)  το ρυθμό μεταβολής της κινητικής ενέργειας του σώματος Σ1 τη στιγμή που ανιχνεύει συχνότητα fΑ=680Ηz.
Δίνεται η ταχύτητα διάδοσης του ήχου στον αέρα, 340m/s

α)   k  =  m₁  ω²  =>     400  =  1  ω²  =>  ω = 20 rad/s             f =  ω / 2π  =  20/2π  = 10/π Hz             T = π/10 s

  x(t)  =  0,4 ημ20t               υ(t)  =  8 συν20t               α(t)  =  - 160 ημ20t       

όταν διέρχεται το Σ₁   από τη θέση ισορροπίας του  έχει ταχύτητα  υ = 8 m/s  

β)   κεντρική ελαστική κρούση 

  v₁'  =  v₁  (m₁ - m₂) / (m₁ + m₂)  =  8  ( 1 - 3 ) / ( 1 + 3 )  =>     v₁'  =  - 4 m/s

  v₂'  =  2 v₁ m₁ / (m₁ + m₂)  =  2 8 1 / ( 1 + 3 )  =>   v₂'  =  4 m/s

γ)    το Σ₁  μετά την κρούση βρίσκεται στη θέση ισορροπίας του  και έχει ταχύτητα  v₁' = - 4 m/s 

   1/2  k  (A')²  =  1/2  m₁ ( v₁')²   =>   A'  =  (4 m/s)  /  (20 rad/s)   =>   A' = 0,2 m        

  x(t)  =  0,2 ημ(20t +π)               υ(t)  =  4 συν(20t + π)               α(t)  =  - 80 ημ(20t + π)    

  x(t)  =  0,2 ημ(20t +π)  =>    - 0,1 3^1/2  =  0,2 ημ(20t +π)   =>    ημ(20t +π)  =  - 3^1/2 / 2  =  ημ(4π/3)  ή  ημ(5π/3) 

           20t + π  =  2Νπ  +  4π/3  =>   20t  =  2Νπ  + π/3  =>   t  =  Ν π/10  + π/60    Ν = 0, 1, 2, 3, ...  

           20t + π  =  2Νπ  +  5π/3  =>   20t  =  2Νπ  + 2π/3  =>  t  =  Ν π/10  +  π/30    Ν = 0, 1, 2, 3, ...    

Ν = 0    t  =  Ν π/10  + π/60  =  π/60 s          Ν = 1    t  =   π/10  + π/60  =  7π/60 s    

Ν = 0    t  =  Ν π/10  + π/30  =  π/30 s  =  2π/60 s          Ν = 1    t  =   2π/10  + π/30  =  7π/30 s  =   14π/60 s   

1η φορά :   t  =  π/60 s    τότε   υ(π/60)  =  4 συν(20 π/60 + π)  =  4 συν(π + π/3)  =  4  συνπ  συν(π/3)  =  - 2 m/s

        f_A  =  f_S  ( v - |v₁|) / ( v + v₂')  =  688  ( 340 - 2 ) / ( 340 +4 )  =   688  338 / 344  =  2  338 Hz  =  676 Hz

2η φορά :   t  =  π/30 s   τότε   υ(π/30)  =  4 συν(20 π/30 + π)  =  4 συν(2π/3 + π)  =  4  συνπ  συν(2π/3) =  +2 m/s

        f_A  =  f_S  ( v + |v₁|) / ( v + v₂')  =  688  ( 340 + 2 ) / ( 340 +4 )  =   688  342 / 344  =  2  342 Hz  =  684 Hz

δ)    f_A  =  f_S  ( v + v₁ ) / ( v + v₂')  =>    680   =  688  ( 340 + υ₁ ) / ( 340 +4 ) =>   680   =  2  ( 340 + υ₁ )  =>  

           =>   340   =   340 + υ₁   =>   υ₁  =  0    το  Σ₁  διέρχεται από ακραία θέση  άρα  dK/dt  =  m₁  v  a  =  0 

Γ3.   Το περιπολικό ξεκινά από το μέσον M του ευθύγραµµου τµήµατος ΑΒ κινούµενο προς τον Β µε σταθερή ταχύτητα.  Τη χρονική στιγµή που ξεκινά θέτει σε λειτουργία την σειρήνα και την διακόπτει τη στιγµή που φτάνει µπροστά από τον Β.  Οι ακίνητοι παρατηρητές χρονοµέτρησαν και διαπίστωσαν ότι ακούνε τον ήχο ο µεν Α επί 18 s , ο δε Β επί 16 s.      Α         S ^υs®          B
α)   Με ποια ταχύτητα κινείται το περιπολικό;
β)   Επί πόση ώρα άκουγε την σειρήνα ο οδηγός του περιπολικού;
γ)   Πόσο απέχουν οι παρατηρητές;
δ)   Ποια είναι η σχέση που συνδέει το μήκος κύματος, λ του ήχου που εκπέμπει η πηγή με τα μήκη κύματος που ακούνε οι δύο παρατηρητές;         Η ταχύτητα του ήχου είναι 340 m/s.
ΑΠ: α) 20m/s, β) 17s γ) 680m, δ) λ_Α+λ_Β=2λ

   f_A  =  f_S   v / ( v + v_S )   =>     N / t_A  =  f_S   v / ( v + v_S )   =>   N / 18  =  f_S   340 / ( 340 + v_S )     (1)

   f_B  =  f_S   v / ( v - v_S )   =>     N / t_B  =  f_S   v / ( v - v_S )   =>   N / 16  =  f_S   340 / ( 340 - v_S )        (2)

(1) / (2)  =>  16/18  = ( 340 - v_S ) / ( 340 + v_S )  =>  8 ( 340 + v_S ) = 9 ( 340 - v_S )  =>  17 v_S = 340  => v_S = 20 m/s

 N  =  f_S  t_S   =  f_A  t_A  =  f_B  t_B    =>  t_S  =  t_A  f_A / f_S  =  t_A  v / ( v + v_S )  =  18   340 / ( 340 + 20 )  =  17 sec 

  (MB)  =  v_S  t_S  =  20 m/s  17 s  =  340 m = (MA)       συνεπώς       (AB)  =  680 m

  λ_Α  =  λ  +  υ_S Τ   =  υ / f_S  +  υ_S / f_S  =  ( υ + υ_S ) / f_S 

  λ_Β  =  λ  -  υ_S Τ   =  υ / f_S  -  υ_S / f_S  =  ( υ - υ_S ) / f_S      τελικά    λ_Α  +  λ_Β  =  2 λ

Γ4.    Τρία οχήματα  A, B  και Γ κινούνται σε ευθύγραμμο αυτοκινητόδρομο. Τα μέτρα των ταχυτήτων
τους είναι υ₁=20m/s, υ₂=30m/s  και  υ₃=20m/s αντίστοιχα. Τα οχήματα Α και Β κινούνται προς την ίδια κατεύθυνση και προπορεύεται το όχημα Α, ενώ το όχημα Γ έρχεται από την αντίθετη κατεύθυνση.  Το όχημα Β εκπέμπει ήχο συχνότητας f_s=930Ηz. 

                      Β ^υ2®         Α ^υ1®               ^υ3¬  Γ
α)   Να υπολογίσετε τη συχνότητα του ήχου που αντιλαμβάνεται ο οδηγός του οχήματος Α .
β)   Να υπολογίσετε το μήκος κύματος του ήχου που αντιλαμβάνεται ο οδηγός του οχήματος Γ.
γ)   Τα οχήματα Β και Γ διασταυρώνονται, οπότε στη συνέχεια απομακρύνεται το ένα από το άλλο,
να υπολογίσετε τη νέα συχνότητα του ήχου που αντιλαμβάνεται ο οδηγός του οχήματος Γ.
δ)   Ο οδηγός του οχήματος Α τη χρονική στιγμή t=0, ενώ προηγείται του οχήματος Β, πατάει γκάζι και προσδίδει στο όχημά του σταθερή επιτάχυνση α=2m/s²  για χρονικό διάστημα 5s,
παραμένοντας σε όλη τη διάρκεια της επιταχυνόμενης κίνησης προπορευόμενος του οχήματος Β.
Να σχεδιάσετε το διάγραμμα της συχνότητας που αντιλαμβάνεται ο οδηγός Α συναρτήσει του
χρόνου σε αριθμημένους άξονες για το χρονικό διάστημα των 5s.
ε)   Να υπολογίσετε τον αριθμό των παλμών που αντιλαμβάνεται ο οδηγός του οχήματος Α στη
διάρκεια των 5s.
Δίνεται η ταχύτητα του ήχου στον αέρα υ=340m/s .
Απ:α) 960Ηz, β) 1/3m, γ) 804Ηz, δ) f=960-6t. ε)4725παλμοί

α)   f_A  =  f_S  ( v - v₁ ) / ( v - v₂ )  =>  f_A  = 930  ( 340 - 20 ) / ( 340 - 30 )  =  930  320 / 310  =  3  320  =  960 Hz   

β)  λ_Γ  =  λ  -  υ₂ Τ   =  υ / f_S  -  υ_S / f_S  =  ( υ - υ_S ) / f_S   =  ( 340 - 30 ) / 930  = 1/3 m

γ)   f_Γ  =  f_S  ( v + v₁ ) / ( v - v₂ )  =>  f_Γ  = 930  ( 340 + 20 ) / ( 340 - 30 )  =  930  360 / 310  =  3  360  =  1080 Hz   

      f_Γ '  =  f_S  ( v - v₁ ) / ( v + v₂ )  =>  f_Γ '  = 930  ( 340 - 20 ) / ( 340 + 30 )  =  930  320 / 370  =  804,3 Hz  

δ)    υ₁  =  20  +  2t          f_A  =  f_S  ( v - v₁ ) / ( v - v₂ )  =>  f_A  = 930  ( 340 - 20 - 2t ) / ( 340 - 30 )  =  930  ( 320 - 2t ) / 310  =  3  ( 320 - 2t )  =  960 - 6t   (Hz)    

ε)    dN/dt  =   960 - 6t  =>   dN =  (960 - 6t) dt  =>   N  =  [ 960t  -  3t² ]_{t=0s => 5s}  =  960  5  -  3  5²  

       =>  N  =  4800  -  3  25  =   4800  -  75  =  4725 παλμοί    από  0s   εώς  5s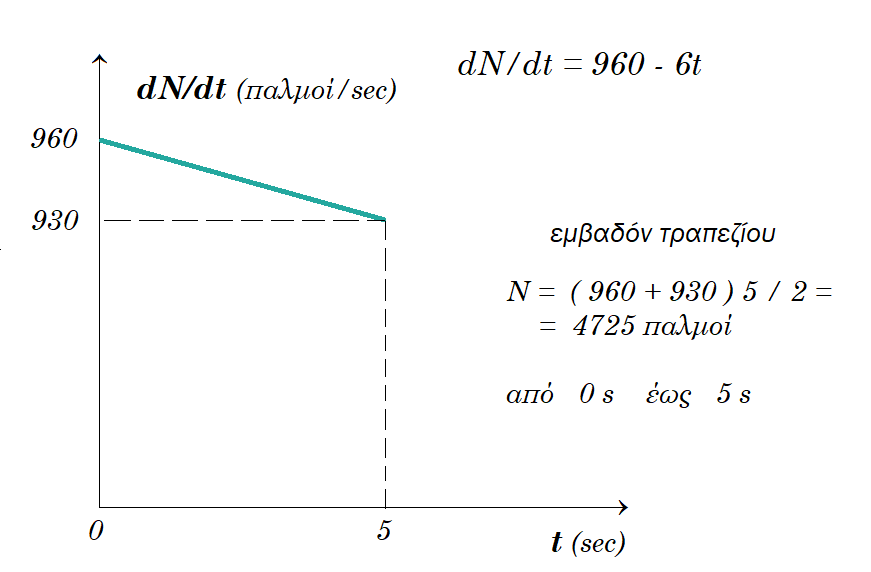     

Γ5.    Σώμα μάζας Μ=2kg ισορροπεί συνδεδεμένο με το άκρο ελατηρίου σταθεράς k=400Ν/m    που κρέμεται από ακλόνητο σημείο.  Βλήμα μάζας m=2kg που κινείται κατακόρυφα προς τα πάνω συγκρούεται με ταχύτητα υ0 = 3½ m/s μετωπικά και πλαστικά με το Μ.  Μετά την κρούση το συσσωμάτωμα κάνει κατακόρυφες ΑΑΤ.

α)  Να υπολογίσετε το πλάτος της ΑΑΤ του συσσωματώματος.
β)  Να γράψετε τη χρονική εξίσωση της ταχύτητας του συσσωματώματος.
γ)  Να υπολογίσετε το ρυθμό μεταβολής της δυναμικής ενέργειας των ταλαντώσεων του   συσσωματώματος εκείνη τη χρονική στιγμή που η δυναμική ενέργεια γίνεται ίση με την κινητική για πρώτη φορά μετά από τη στιγμή που έγινε η κρούση.  Ποιά είναι η  χρονική αυτή στιγμή ;
δ)  Αμέσως μετά την κρούση ενεργοποιείται μηχανισμός που παράγει ήχους σταθερής συχνότητας 1000Ηz.  Εκφράστε την συχνότητα του ήχου που αντιλαμβάνεται ο ακίνητος παρατηρητής Α  συναρτήσει του χρόνου.  Πόση είναι η  μέγιστη / ελάχιστη  συχνότητα που αντιλαμβάνεται για τον ήχο αυτόν.
Να θεωρηθεί ως t0=0 η χρονική στιγμή αμέσως μετά την κρούση και ως θετική, η φορά κατακόρυφα προς τα πάνω.  Το συσσωμάτωμα καθώς ταλαντώνεται δεν προσπερνά τη θέση του παρατηρητή. Δίνονται η ταχύτητα του ήχου υηχ=340m/s,   g=10m/s²  και  3^½ = 1,7.
α. 0,1m, β. υ=συν(10t+π/6) (SI), γ. 20J/s, δ. 1003Ηz

  M g = k x₀  =>  x₀  =  2 10 / 400 =>  x₀  =  0,05 m   επιμήκυνση ελατηρίου στη θέση ισορροπίας του σώματος Μ

κεντρική πλαστική κρούση  -  διατήρηση ορμής :   m v₀  =  (m + M) v₁  =>  v₁  =  2  3^½ / 4  =  3^½/2 m/s         

(m+M) g = k x₁  =>  x₁  =  4 10 / 400 =>  x₁  =  0,1 m   επιμήκυνση ελατηρίου στη θέση ισορροπίας του  συσσώματος   Μ+m    

 αμέσως μετά την κρούση το συσσωμάτωμα  βρίσκεται  υψηλότερα από τη θέση ισορροπίας του  κατά  (x₁ - x₀) = 0,1 - 0,05 = 0,05 m  με ταχύτητα θετική  +3^½/2 m/s (προς τα πάνω)

  ½   k  A²  =   ½  k  (x₁ - x₀)²   +   ½  (m+M) v₁²   =>     400  A²  =   400  0,05 ²   +   4  3/4    =>   400  A²  =   400  0,0025  +  3    =  4  =>   A = 0,1 m     το πλάτος ταλάντωσης του συσσωματώματος    

         k  =  (m+M) ω²  =>  400  =  4  ω²  =>  ω  =  10 rad/s 

  x(t)  =  0,1 ημ(10t + θ)       υ(t)  =  1 συν(10t + θ)  

    x(0)  =  0,05  =>  0,1 ημ(θ) = 0,05  =>  ημθ = 0,5  =  ημ(π/6)   ή   ημ(5π/6)   τότε  συν(π/6) = 3^½/2   ή   συν(5π/6) = - 3^½/2       αλλά επειδή  αμέσως μετά την κρούση το συσσωμάτωμα έχει  ταχύτητα θετική  +3^½/2 m/s (προς τα πάνω)  συμπεραίνουμε ότι  θ = π/6 rad  

  οπότε :    x(t)  =  0,1 ημ(10t + π/6)        υ(t)  =  1 συν(10t + π/6)       α(t)  =  - 10 ημ(10t + π/6)   

  K  =  U  =  E/2    =>   ½  k  x(t)²   =   ½  (m+M) v(t)²   =>   (m+M) ω²  x(t)²   =   (m+M) v(t)²   =>    10²   0,01  ημ² (10t + π/6)   =   συν² (10t + π/6)    =>    ημ(10t + π/6)  =  ± συν(10t + π/6)   =>  εφ(10t + π/6)  =  ± 1   =>   10t + π/6  =  Νπ + π/4  ή  Νπ + 3π/4  

 για 1η φορά  Ν = 0     10t + π/6 = π/4  =>   t =  π/120 s   

x(π/120)  =  0,1 ημ(10 π/120 + π/6)  =  0,1  ημ(π/)  =  0,1  2^½/2       υ(π/120)  =  1 συν(10 π/120 + π/6)  =  συν(π/4)  =   2^½/2 

ρυθμός μεταβολής δυναμικής ενέργειας της ταλάντωσης του συσσωματώματος   dU/dt  =  k  x(t)  v(t)  =  400   0,1 2^½/2   2^½/2   =  20 J/s

δ)    f_A  =  f_S  v_ηχ  / ( v_ηχ + v(t) )  =>  f_A  =  1000  340 / ( 340 + συν(10t + π/6) ) 

μέγιστη συχνότητα συμβαίνει όταν   συν(10t + π/6) = - 1  =>   10t + π/6 = Νπ ,  Ν = 1, 3, 5, ...      τότε    f_A  =  1000  340/339  =  1003 Hz

ελάχιστη συχνότητα συμβαίνει όταν   συν(10t + π/6) = + 1 =>   10t + π/6 = 2Νπ ,  Ν = 0, 1, 2, 3, ...     τότε    f_A  =  1000  340/341  =  997 Hz