Κατά μήκος μιας ελαστικής χορδής, διαδίδεται χωρίς απώλειες, ένα αρμονικό κύμα με ταχύτητα υ=2m/s, πλάτος Α=0,4m και μήκος κύματος λ=2m το οποίο τη στιγμή t_o=0 φτάνει σε ένα σημείο Ο, το οποίο παίρνουμε σαν αρχή του προσανατολισμένο άξονα x΄x, με θετική την προς τα δεξιά κατεύθυνση. Το σημείο Ο απέχει κατά 3m από το άκρο Κ της χορδής, το οποίο έχει προσδεθεί σε κατακόρυφο τοίχο, όπως στο σχήμα, ενώ αρχίζει την ταλάντωσή του κινούμενο προς την θετική κατεύθυνση του άξονα y, προς τα πάνω.

1. Να γράψετε την  εξίσωση της απομάκρυνσης του σημείου Ο, σε συνάρτηση με το χρόνο, καθώς και την εξίσωση του κύματος y₁=f(x,t),για  το κύμα που διαδίδεται προς τα δεξιά.
2. Να βρεθεί η εξίσωση της απομάκρυνσης, εξαιτίας του παραπάνω κύματος, του σημείου Σ στην θέση x₁=2,5m.
3. Αφού βρείτε την εξίσωση y=f(t) για την απομάκρυνση του άκρου Κ της χορδής εξαιτίας του ανακλώμενου κύματος, να βρείτε την εξίσωση y₂=f(x,t) για το κύμα το οποίο ανακλάται στο Κ.
4. Να βρείτε την εξίσωση της απομάκρυνσης του σημείου Σ, εξαιτίας του κύματος το οποίο διαδίδεται προς τα αριστερά, καθώς και την εξίσωση y=f(t) της απομάκρυνσής του, λόγω συμβολής των  δύο κυμάτων.
5. Αφού βρείτε την εξίσωση του στάσιμου κύματος που δημιουργείται πάνω στην χορδή, να σχεδιάσετε την μορφή της στην περιοχή μεταξύ των σημείων Ο και Κ, τη χρονική στιγμή t=2,25s. Να υπολογίσετε την παραπάνω στιγμή την ταχύτητα ταλάντωσης του σημείου Σ.

  v = λ / Τ  =>  Τ = 1 s     f = 1 Hz     ω = 2π rad/s 

y = A ημ2π(t/T – x/λ)  =>  y = 0,4 ημ2π(t – x/2)  =>  y = 0,4 ημ(2πt – πx)          y_(O) = 0,4 ημ(2πt)  t > 0

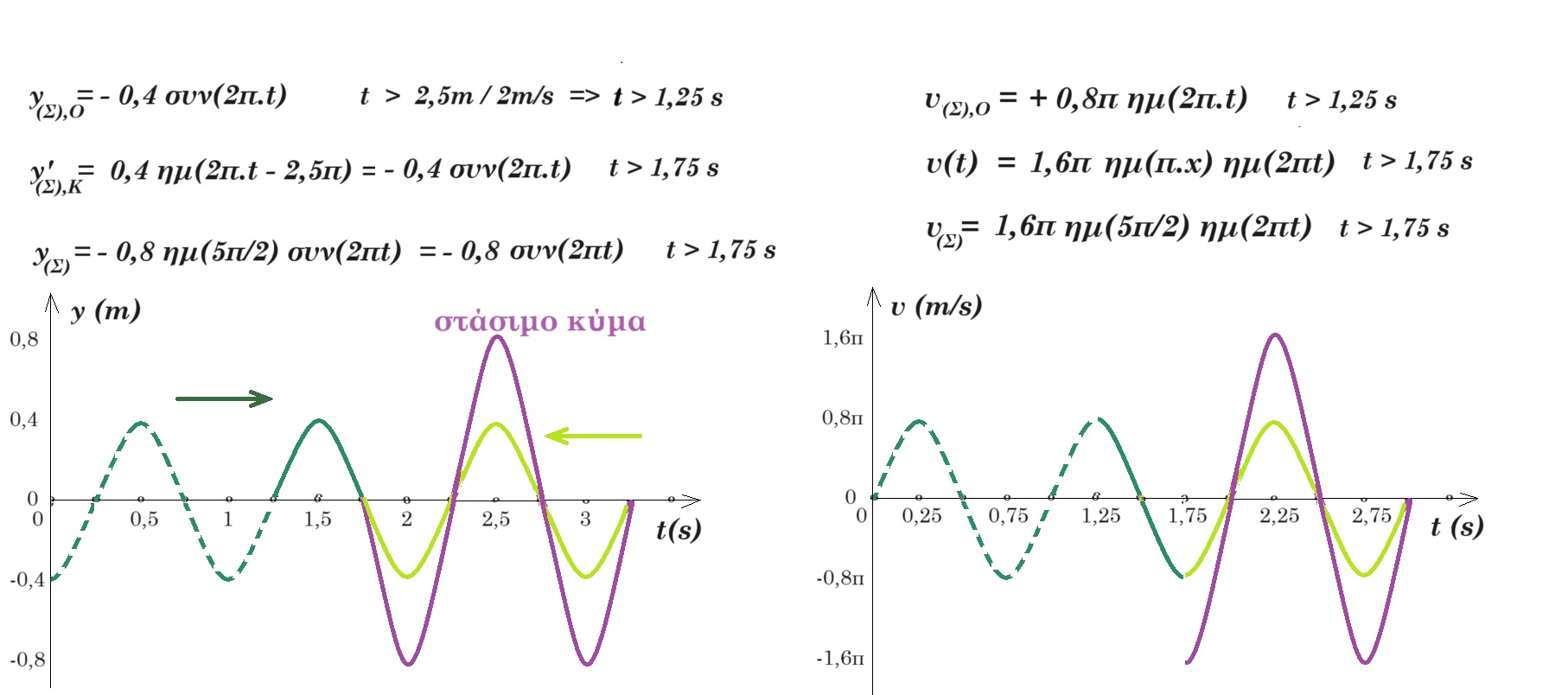
y_(Σ),O = 0,4 ημ(2π.t – π.2,5)  =>  y_(Σ),O = - 0,4 συν(2π.t)    (1)     t > 2,5/2 = 1,25 s 

το κύμα φθάνει στο Κ :  y_(Κ) = 0,4 ημ(2π.t – π.3)    t > 1,5 s  

το κύμα ανακλάται στο Κ  και παρουσιάζει διαφορά φάσης  π  (ακλόνητο σημείο)  y_(Κ) = 0,4 ημ(2π.t – π.3 + π)  =>  y_(Κ) =  0,4 ημ(2π.t - 2π)      t > 1,5 s 

το κύμα από το Κ  φθάνει στο Σ  μετά από χρόνο  τ = (3m - x_(Σ)) / 2m/s = (1,5 - x/2) s = (1,5 - 2,5/2) s = 1/4 s = 0,25 s   και  από το Ο  τ' = 3/2 s + 1/4 s = 7/4 s =  1,75 s

y'_(Σ),K = 0,4 ημ(2π.(t - (1,5 - x_(Σ) /2)) - 2π) =  0,4 ημ(2π.t + π.x_(Σ) - 3π - 2π)  => y'_(Σ),K,  =  0,4 ημ(2π.t + π.x_(Σ) - 5π)    => y'_(Σ),K  =  0,4 ημ(2π.t + π.2,5 - 5π)   => y'_(Σ),K  =  0,4 ημ(2π.t - 2,5π)    t > 1,75 s   (2)       

(1) , (2) =>  y_{(Σ) συνολικά} = 0,8 ημ(2π.t – 5π/2)         έχουμε κοιλία

  υ_(Σ)  = 0,8 2π συν(2π.t – 5π/2)  =  1,6.π συν(2π.t – 5π/2)  

  t = 2,25 s    υ_(Σ)  =  1,6.π συν(2π.2,25 – 2,5.π)  =  1,6.π συν(2π) = + 1,6.π m/s

στο σημείο Σ φθάνουν δύο κύματα  α) από το σημείο Ο  που κινείται προς τα δεξιά  και  β) από το σημείο Κ  που κινείται προς τα αριστερά    τα δύο κύματα συμβάλλουν 

      0,4 ημ(2πt – πx)  +  0,4 ημ(2π.t + π.x - 5π)  = 

=  0,8  ημ(2πt – πx  +  2π.t + π.x - 5π) / 2    συν [ 2πt – πx  -  (2π.t + π.x - 5π) ] / 2  =   

=  0,8  ημ(2πt - 5π/2)   συν(- π.x + 5π/2)  =  0,8  συν(- π.x + 5π/2)  ημ(2πt - 5π/2)   =

=  0,8  συν(5π/2 - π.x)  ημ(2πt - 5π/2)   =  0,8  ημ(π.x)  [ - συν(2πt) ]  =  - 0,8 ημ(π.x) συν(2πt)  =  y_{(Σ) συνολικά}

στο σημείο  - 0,8 ημ(π.x) συν(2πt)  =  y_(Σ)   

  t = 2,25 s     υ_(Σ)  =  - 0,8 ημ(π.2,5) 2π [- ημ(2π. 2,25) ]  =  + 1,6π  1  ημ(4,5π)  = + 1,6π m/s

το κύμα από το σημείο Ο σε χρόνο 2,25 s   διανύει  διάστημα  2,25 s  2 m/s  = 4,5 m = 3 m (= OK)  + 1,5 m         είναι στη θέση   x = 1,5 m             ενώ το κύμα από το σημείο Κ  σε χρόνο 2,25 s - 1,5 s = 0,75 s   διανύει  διάστημα  0,75 s  2 m/s  = 1,5 m          άρα συμβαίνει συμβολή κυμάτων  από τη θέση  x = 1,5 m  έως τη θέση  Κ  x_Κ = 3 m     για χρονικό διάστημα  0,75 s = 3 Τ/4      ενώ  από το σημείο Ο  θέση x = 0 m      έως τη θέση x = 1,5 m      έχουμε τρέχον κύμα που προέρχεται από το σημείο Ο   

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Κατά μήκος μιας ελαστικής χορδής έχει δημιουργηθεί στάσιμο κύμα. Στο άκρο Ο της χορδής που βρίσκεται στη θέση x=0 δημιουργείται κοιλία που τη χρονική στιγμή t=0 βρίσκεται στη θέση ισορροπίας της ταλάντωσής της με υ>0. Η ταχύτητα διάδοσης των τρεχόντων κυμάτων η συμβολή των οποίων δημιούργησε το στάσιμο κύμα είναι υ_δ=2cm/s. Η γραφική παράσταση της απομάκρυνσης ταλάντωσης με το χρόνο ενός σημείου Μ που βρίσκεται στη θέση x=3λ/8, όπου λ το μήκος κύματος των κυμάτων που συμβάλουν, φαίνεται στο διάγραμμα.
Γ1. Να αποδείξετε ότι το πλάτος Α των κυμάτων που συμβάλουν είναι Α=2cm.   [Μονάδες 5]
Γ2. Να γράψετε την εξίσωση του στάσιμου κύματος.   [Μονάδες 5]
Γ3. Να βρείτε πόσες φορές διέρχεται από τη Θ.Ι της ταλάντωσής του το σημείο Μ σε χρονικό
διάστημα 10sec.   [Μονάδες 5]
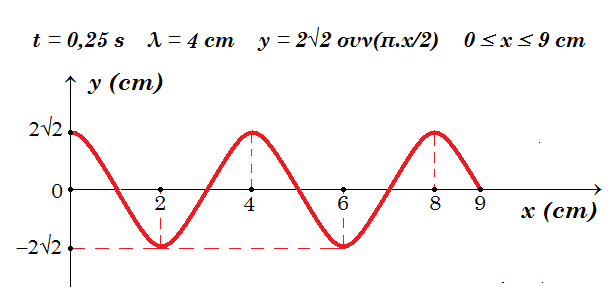
Γ4. Να γίνει το στιγμιότυπο του στάσιμου κύματος από x=0 εως x=9cm τη χρονική στιγμή t=0,25s.
[Μονάδες 5]
Γ5. Να βρεθεί το μέτρο της ταχύτητας ταλάντωσης και το μέτρο της επιτάχυνσης ταλάντωσης του σημείου Μ όταν η απομάκρυνση του από τη Θ.Ι. είναι y= √2cm.   [Μονάδες 5]

  x_M = 3λ/8 = 3/2 cm     t = 3/2 cm / 2 cm/s = 3/4 s

y_M = 2A συν(2π.x_M /λ) ημ(2π.t/Τ)  =>  -2√2 = 2A συν(2π.(3/2)/4) ημ(2π.(1/2)/2)  =>  

     =>  -2√2 = 2A συν(3π/4) ημ(π/2)  =>  -2√2 = 2A (-√2/2)  1  =>  A = 2 cm

2A |συν(2π.x_M /λ)| = |Α'|  =>  2A |συν(2π.(3/2) /4)| = |±2√2|  =>

    =>  2A |συν(3π/4)| = 2√2  =>  A |(-√2/2)| = √2  =>  Α = 2 cm

Γ2.    y = A ημ2π(t/T – x/λ)  =>  y = 2 ημ2π(t/2 – x/4)  =>  y = 2 ημ(πt – πx/2)          

Γ3.    y = 5 ταλαντώσεις   t / T = 10 s / 2 s 

Γ4.     t = 0,25 s    y = 2A συν(2π.x/λ) ημ(2π.t/Τ) = 4 συν(2π.x/4) ημ(2π.0,25/2)  = 4 συν(π.x/2) ημ(π/4) = 4 συν(π.x/2)  √2/2  = 2√2 συν(π.x/2)  

Γ5.     y_M = 2Α συν(2π.x_M /λ) ημ(2π.t/Τ)  =>  √2 = 4 συν(2π.(3/2)/4) ημ(2π.t/Τ)  =>

      =>  √2 =  4 συν(3π/4) ημ(2π.t/Τ)  =>  √2 =  4 (-√2/2) ημ(2π.t/Τ)  =>  - 1/2 = ημ(2π.t/Τ) 

    συν(2π.t/Τ)  =  ± √3/2   

   v_M = 2Α 2π/Τ συν(2π.x_M /λ) συν(2π.t/Τ)   =>   v_M = 4 2π/2 συν(2π.(3/2)/4) (± √3/2 )   =>

               =>   v_M = ± 4.π (±√2/2) (-√3/2)  =>  v_M = ±√6.π cm/s

   a_M = - 2Α (2π/Τ)²  συν(2π.x_M /λ) ημ(2π.t/Τ)  =>  α_M =  - 4  (2π/2)²  συν(2π.(3/2)/4) (-1/2 )  =>

               =>   α_M = - 4 π² (±√2/2) (-1/2)  =>  α_M = ± √2.π² cm/s²    

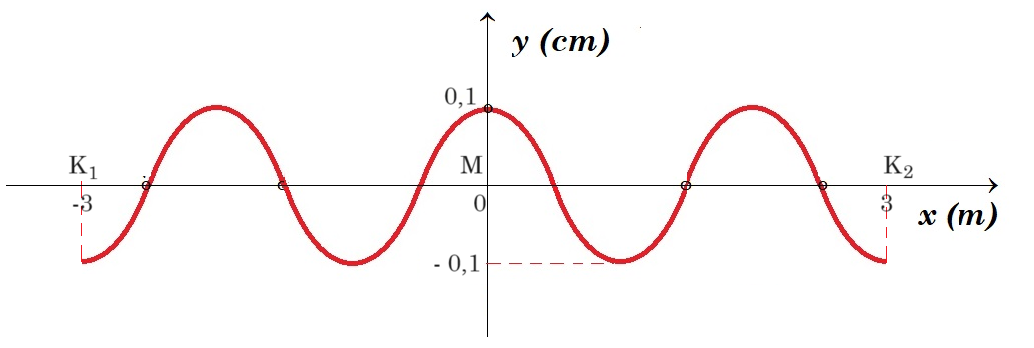
Δύο σημεία Κ1 και Κ2 ενός γραμμικού ομογενούς ελαστικού μέσου απέχουν απόσταση (Κ1Κ2)=6m. Δύο αρμονικά κύματα που διαδίδονται πάνω στην ευθεία Κ1Κ2 με αντίθετες κατευθύνσεις, φτάνουν ταυτόχρονα στο μέσο Μ του ευθύγραμμου τμήματος Κ1Κ2 και αναγκάζουν το υλικό σημείο στο μέσο Μ να κινηθεί προς τα πάνω.
Λαμβάνουμε ως θετική φορά κίνησης προς τα πάνω.
Θεωρούμε ότι τα δύο κύματα έχουν την ίδια ταχύτητα διάδοσης κατά μέτρο, ίδιο πλάτος και την ίδια συχνότητα. Αρχή του άξονα x΄x ορίζουμε το μέσο Μ και θετική φορά από το Μ προς το Κ2. Ως χρονική στιγμή to=0 ορίζουμε τη στιγμή που τα δυο κύματα φτάνουν στο μέσο Μ.
Από τη συμβολή των δυο κυμάτων προκύπτει στάσιμο κύμα για το οποίο παρατηρούμε:
α. Τα σημεία Κ1 και Κ2 είναι κοιλίες.
β. Μεταξύ των σημείων Κ1 και Κ2 δημιουργούνται 5 κοιλίες ( οι κοιλίες στα σημεία Κ1,Κ2 δεν περιλαμβάνονται).
γ. Οι ακραίες θέσεις μιας κοιλίας απέχουν 0,4m.
δ. Ο χρόνος που χρειάζεται μια κοιλία για να περάσει δύο διαδοχικές φορές από τη θέση ισορροπίας της είναι 2s.
Γ1. Να υπολογίσετε το πλάτος, το μήκος κύματος και την ταχύτητα διάδοσης καθενός από τα κύματα που συμβάλουν. (Μονάδες 6)
Γ2. Να γράψετε την εξίσωση του στάσιμου κύματος που δημιουργείται. (Μονάδες 4)
Γ3. Να βρείτε τη χρονική στιγμή που τα δύο κύματα συμβάλουν σε ένα σημείο Ν του γραμμικού ελαστικού μέσου, το οποίο βρίσκεται στη θέση xN=5m
Να υπολογίσετε την επιτάχυνση του σημείου Ν τη χρονική στιγμή t1=5s. (Μονάδες 5)
Γ4. Να γίνει το στιγμιότυπο του στάσιμου κύματος που έχει δημιουργηθεί στο ελαστικό μέσο τη χρονική στιγμή t2 = 7s. (Μονάδες 5)
Γ5. Να βρεθεί το διάστημα που έχει διανύσει το σημείο Μ από τη χρονική στιγμή t0=0s έως τη χρονική στιγμή t3 = 8,5s. (Μονάδες 5)
Δίνεται π²=10 , √2 = 1,4

K₁K₂ = 6 m  = 12 λ/4  =>  λ = 2 m           4A = 0,4 m  =>  A = 0,1 m     T/2 = 2 s => T = 4 s       

    v = λ/T = 2m / 4s = 0,5 m/s     

  κK₁   δ    κ    δ    κ   δ    κM   δ   κ    δ    κ   δ    κΚ₂    

  y = 0,2 συν(2πx/0,5) ημ(2πt/4)  => y = 0,2 συν(4πx) ημ(πt/2)

  y_M = 0,1 ημ(π 8,5/2) = 0,1 ημ(π/4)  = 0,1  0,7 = 0,07 m            0,8 + 0,07 = 0,87 m

  t = 5m / 0,5m/s = 10 s      

   y_N  =  0,1 ημ(2πt/4 + 2πx/0,5) =>   y_N = 0,1 ημ(πt/2 + 4πx)

    y_N = 0,1 ημ(π5/2 + 4π 5) = 0,1 ημ(π/2) = 0,1 m

  v_N = 0,05π συν(πt/2 + 4πx)        

    a_N = - 0,25 ημ(πt/2 + 4πx)             a_N = - 0,25 ημ(π/2) = - 0,25 m/s²       

(α) Να γράψετε ποια σημεία του στάσιμου κύματος ονομάζονται δεσμοί και ποια ονομάζονται κοιλίες.
(β) Το πιο κάτω σχήμα δίνει το στιγμιότυπο ενός στάσιμου κύματος, με περίοδο Τ και μήκος κύματος λ, τη χρονική στιγμή 𝑡 = T/6.

Το σημείο στη θέση x = 0 αντιστοιχεί σε κοιλία του στάσιμου κύματος και τη χρονική στιγμή  t = 0 διέρχεται από τη θέση ισορροπίας με θετική ταχύτητα. Να γράψετε τις εξισώσεις των τρεχόντων κυμάτων που παράγουν το στάσιμο κύμα  αν η ταχύτητα διαδόσεώς τους είναι υ = 0,6 m/s

 εξίσωση στασίμου κύματος :     y(x , t)  =  2A  συν(2πx/λ)  ημ(2πt/Τ)           

   τ = Τ/6   

  y  =  2A  συν(2πx/λ)  ημ(2π (Τ/6) /Τ)  =  2A  συν(2πx/λ)  ημ(π/3)  =  2A  συν(2πx/λ)  3^½/2  =  3^½A  συν(2πx/λ)  

από το σχήμα έχουμε  0,1 3^½ = 3^½ Α  =>  Α = 0,1 m         και    5 λ/4 = 1,5 m  =>  λ  =  1,2 m

   v =  λ / T  =>   0,6 m/s  =  1,2 m / T  =>  T = 2 s

εξισώσεις τρεχόντων κυμάτων :  y₁  =  0,1 ημ(2πt/2 - 2πx/1,2) =  0,1 ημ(πt - 5πx/3)    &   y₂  =  0,1 ημ(πt + 5πx/3)

    στάσιμο κύμα

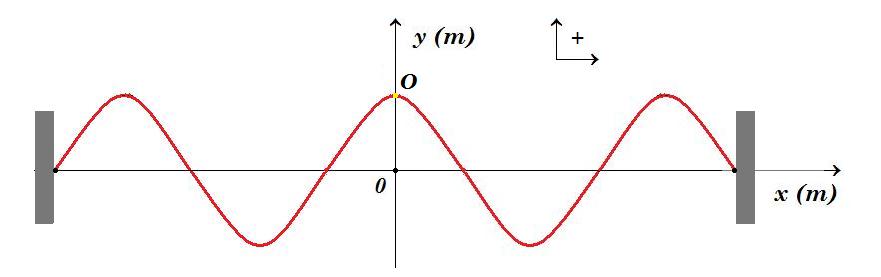
Πάνω σε χορδή μήκους l=1m, με σταθερά τα δυο άκρα της, έχει σχηματισθεί ένα στάσιμο κύμα και στο σχήμα βλέπετε την μορφή της χορδής, μια στιγμή t=0, όπου η κοιλία στο σημείο Ο, βρίσκεται σε μέγιστη απομάκρυνση.  Αν το σημείο Ο αποκτά μέγιστη κατά μέτρο ταχύτητα 0,628m/s τη χρονική στιγμή t₁=0,05s, για πρώτη φορά, ζητούνται:

1. Η ταχύτητα διάδοσης ενός (τρέχοντος) κύματος πάνω στην χορδή αυτή.
2. Να γραφούν οι εξισώσεις της απομάκρυνσης (y=f(t)) και της ταχύτητας του σημείου Ο (υ=f(t)) σε συνάρτηση με τον χρόνο, θεωρώντας τον προσανατολισμό που δίνεται στο σχήμα.
3. Θεωρώντας την θέση του σημείου Ο, σαν αρχή ενός συστήματος αξόνων x,y, όπως στο σχήμα :

• α) Πόσα ακόμη σημεία ταλαντώνονται με το ίδιο πλάτος με το Ο;
• β) Ποια η εξίσωση y=f(x,t) για το στάσιμο κύμα το οποίο έχει δημιουργηθεί πάνω στην χορδή;
• γ) Να βρεθεί η εξίσωση της απομάκρυνσης και της επιτάχυνσης σε συνάρτηση με το χρόνο, για ένα σημείο της χορδής Σ, το οποίο βρίσκεται στην θέση x=-0,2m.
• δ) Να κάνετε τις γραφικές παραστάσεις της απομάκρυνσης σε συνάρτηση με το χρόνο (y=f(t)), για τα σημεία Σ και Ο της χορδής, στους ίδιους άξονες.

1.  6 δεσμοί,  5 κοιλίες    y = 2A συν(2πx/λ) ημ(2πt/Τ)     υ = 2A 2π/Τ συν(2πx/λ) συν(2πt/Τ)    

            Τ/4 = 0,05s  =>  T = 0,2 s                      l = 5 λ/2  =>  λ = 2 l/5 = 2 1/5 m = 0,4 m

   v_max =  0,628 = 2A 2π/0,2 συν(2π0/λ)   =>  0,628 = 2A 10 3,14    =>  A = 0,01 m      

                  υ = λ / Τ  =  0,4m / 0,2s =>  v = 2 m/s     

2.      y_(O) = 2 0,01 συν(2π 0/0,4) συν(2πt/0,2) = 2 0,01  1  συν(10πt) =>    y_(O) =  0,02 συν(10πt)      

          υ_(O) = - 0,2π ημ(10πt)        α_(O) = - 2π² συν(10πt)  

  τη στιγμή t = 0  το σημείο Ο  βρίσκεται σε μέγιστη απομάκρυνση   οπότε η ταχύτητα είναι μηδέν

3α.   συνολικά  5 κοιλίες      

3β.   y = 2A συν(2πx/λ) ημ(2πt/Τ + π/2)  =>    y = 0,02 συν(2πx/0,4) ημ(2πt/0,2 + π/2)   =>    y = 0,02 συν(5πx) ημ(10πt + π/2)   ή     y = 0,02 συν(5πx) συν(10πt) 

υ = 0,2π συν(5πx) συν(10πt + π/2)   ή     υ = - 0,2π συν(5πx) ημ(10πt) 

α = - 2π² συν(5πx) ημ(10πt + π/2)   ή     α = - 2π² συν(5πx) συν(10πt) 

3γ.   y_Σ = 0,02 συν(5π(-0,2)) ημ(10πt + π/2)  =>   y_Σ = 0,02 συν(-π) ημ(10πt + π/2)   =>   y_Σ = - 0,02 ημ(10πt + π/2)   ή   y_Σ = - 0,02 συν(10πt)

         υ_Σ = - 0,2π συν(10πt + π/2)   ή   υ_Σ = + 0,02 ημ(10πt)

         α_Σ =  2π² ημ(10πt + π/2)   ή   α_Σ =  2π² συν(10πt)

3δ.   y_Ο = 0,02 συν(5π(0)) ημ(10πt + π/2)  =>   y_Ο = 0,02 συν(0) ημ(10πt + π/2)   =>   y_Ο = + 0,02 ημ(10πt + π/2)   ή   y_Ο = + 0,02 συν(10πt)

         υ_Ο = + 0,2π συν(10πt + π/2)   ή   υ₀ = - 0,02 ημ(10πt)

         α_Ο = - 2π² ημ(10πt + π/2)   ή   α_Ο = - 2π² συν(10πt)

1.   Μια πηγή κυμάτων παράγει 12 παλμούς σε 2 s.  Ποιά είναι η περίοδος των κυμάτων και ποιά η συχνότητα της πηγής;  Αν χρειάζεστε κύματα με μεγαλύτερο μήκος κύματος θα αυξήσετε ή θα μειώσετε τον αριθμό των παλμών που δίνει η πηγή στα 2 s; 

συχνότητα παλμών =  12 παλμοί / 2 s  =  6 s^-1  =  6 Hz  

 περίοδος κυμάτων :  T = 1/f  = 1/6 s    

τα κύματα διαδίδονται στο μέσο με ταχύτητα  υ = λ/Τ  = λ f

αν θέλουμε κύματα με με μεγαλύτερο μήκος κύματος  λ ,  επειδή η ταχύτητα τους εξαρτάται από το μέσον διάδοσης άρα είναι σταθερή,  θα πρέπει να μειώσουμε την συχνότητα  δηλαδή να μειώσουμε τον αριθμό των παλμών στα  2 s

2.   Σε μια λεκάνη με νερό, στην επιφάνεια, ένα μικρό κομμάτι φελλού μάζας  6 g  ταλαντώνεται  λόγω των κυμάτων που διαδίδονται στην επιφάνεια του νερού με ταχύτητα  υ = 0,2 m/s. Τα κύματα έχουν πλάτος ταλάντωσης  Α = 5 mm και μήκος κύματος  λ = 6 mm.  Να βρεθεί η μέγιστη κινητική ενέργεια του φελλού. 

  m = 6 g = 6 10^-3 kg              v = λ f  =>   0,2 = 0,006  f   =>  f  =  200/6 = 100/3 Hz

   ω  =  2π f  =  200π/3 rad/s        v_max  = ω A  =  200π/3 rad/s  5 10^-3 m  =  π/3 m/s  

  K_max  =  0,5  m  v_max²  =  0,5  6 10^-3   (π/3)²  =   π²/3 10^-3 J  

3.   Ένας μαθητής κάθεται στο λιμάνι και παρατηρεί μια βάρκα που κινείται στον ρυθμό των κυμάτων της θάλασσας.  Διαπιστώνει ότι ο χρόνος ώστε να πάει η βάρκα από το ανώτατο  στο κατώτατο σημείο της ταλάντωσής της  απόσταση περίπου 9 m είναι  Δt = 3 s.  Αν οι διαδοχικές κορυφές απέχουν 9 m να βρεθεί

α)  η ταχύτητα των κυμάτων 

β)  το μέτρο της μέγιστης επιτάχυνσης της βάρκας

η απόσταση από την ανώτατη θέση έως την κατώτατη : 2A = 9m  =>  A = 4,5 m     σε χρόνο μισής περιόδου :  T/2 = 3s  => T = 6s       οι διαδοχικές κορυφές απέχουν  λ = 9m   η ταχύτητα των κυμάτων είναι :   v = λ/T  =  9m / 6s = 1,5m/s   κυκλική συχνότητα  ω = 2π/Τ = 2π/6 = π/3 rad/s   η μέγιστη επιτάχυνση της βάρκας  α_max = ω²Α = (π/3)² 4,5 » 5 m/s²

4.   Σε κάποιο ελαστικό μέσο διαδίδεται γραμμικό αρμονικό κύμα με εξίσωση :  y = A ημ2π( t/Τ - x/λ ).  Ποιά χρονική στιγμή αρχίζει να ταλαντώνεται ένα σημείο Μ του μέσου που βρίσκεται στην ευθεία διάδοσης του κύματος και απέχει από την πηγή Ο  του κύματος απόσταση  χ_Μ = 5λ/4;  Να παρασταθεί γραφικά συναρτήσει του χρόνου η απομάκρυνση του σημείου Μ από τη θέση ισορροπίας του.

    y = A ημ2π( t/Τ - x/λ )               υ  = (2π/Τ) A  συν2π( t/Τ - x/λ )

  το κύμα φθάνει στο σημείο Μ  σε χρόνο  t  =  x_M / v  =  5λ/4  /  λ/Τ  =  5Τ/4 

      y_Μ  =  A ημ2π( t/Τ - x_Μ /λ )   =     A ημ2π( t/Τ - 5/4 )   =  A ημ(2πt/Τ - 5π/2 )      t > 5T/4

       y_M  =  A ημ(2πt/Τ)  συν(5π/2)  -   A συν(2πt/Τ)  ημ(5π/2)  =   - A συν(2πt/Τ)      t > 5T/4

συν(5π/2) = 0     ημ(5π/2) = 1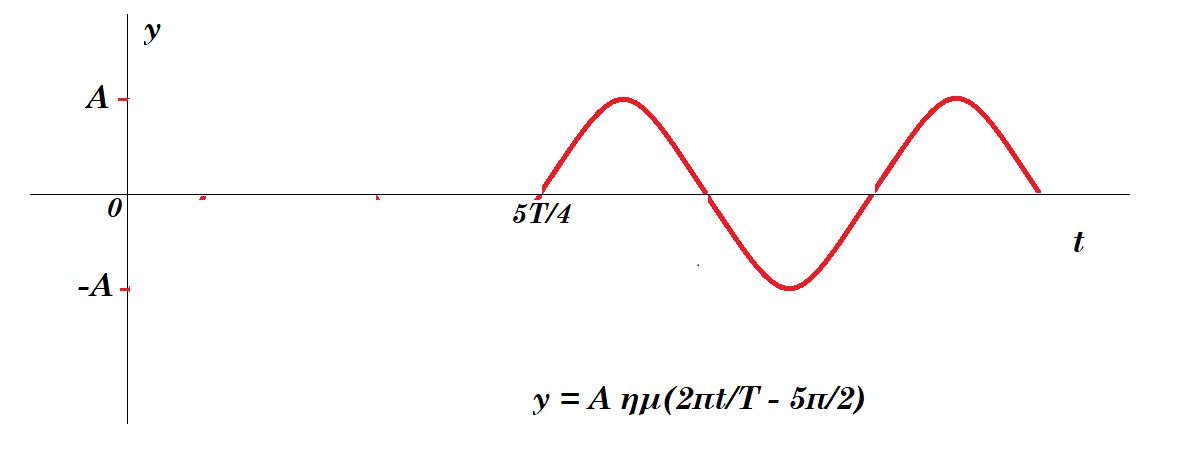       

5.  Έστω η εξίσωση κύματος είναι :    y = 10 ημπ(t - x)    x,y cm   t sec.    Να βρεθεί  η ταχύτητα του κύματος στο μέσον διάδοσής του  και  η ταχύτητα ενός μορίου του μέσου όταν η απομάκρυνσή του από τη θέση ισορροπίας του είναι  y = 6 cm.

y = 10 ημπ(t - x)  =  Α ημ2π(t/Τ - x/λ)            υ  = 10π  συνπ(t - x)

  Α = 10 cm       T = 2 s        λ = 2 cm      υ = λ/Τ =  1 cm/s 

y = 10 ημπ(t - x)  =  6 cm  =>   ημπ(t - x) = 0,6    =>   συνπ(t - x) = ± 0,8    

υ  = 10π  συνπ(t - x) =  ± 8π cm/s    

6.   Κατά μήκος μιας χορδής μεγάλου μήκους, η οποία ταυτίζεται με τον άξονα x′Ox, διαδίδονται ταυτόχρονα δύο αρμονικά κύματα που έχουν εξισώσεις  

        y₁ = 0,1 ημ2π(5t – 2,5x) (S.I.)  και  y₂ = 0,1 ημ2π(5t + 2,5x) (S.I.).
Τα δύο κύματα συμβάλλουν δημιουργώντας στο ελαστικό μέσο στάσιμο κύμα.
α.  Να γράψετε την εξίσωση του στάσιμου κύματος που δημιουργείται στη χορδή,
β.  Να αποδείξετε ότι στην αρχή O(x = 0) του άξονα δημιουργείται κοιλία.
γ.  Να διερευνήσετε αν στο σημείο Ζ(xΖ = 0,5 m) σχηματίζεται δεσμός ή κοιλία,
δ.  Να υπολογίσετε το πλάτος της ταλάντωσης καθώς και τη μέγιστη ταχύτητα ταλάντωσης του υλικού σημείου Μ της χορδής που έχει τετμημένη x_Μ = 1/6 m.

α)   y₁ = 0,1 ημ2π(5t – 2,5x) (S.I.)  και  y₂ = 0,1 ημ2π(5t + 2,5x) (S.I.)      

           y  =  y₁  +  y₂  =  0,2  συν5πx  ημ10πt   

β)  για  x = 0   το πλάτος ταλάντωσης είναι  Α  =  0,2  συν5π0 =  0,2 m  μέγιστο    το σημείο Ο (x = 0) είναι κοιλία

γ)  για  x_Ζ = 0,5 m  το πλάτος ταλάντωσης είναι  Α_Ζ  =  0,2 συν(5π0,5) = 0    άρα το σημείο Ζ (x=0,5m) είναι δεσμός

δ)  για  x_Μ = 1/6 m  το πλάτος ταλάντωσης είναι  Α_Μ =|0,2 συν(5π/6)|= 0,2 |-3^1/2/2| = 0,1 3^1/2 m  

   y  =  0,2  συν5πx  ημ10πt        v  =  2π  συν5πx  συν10πt  

   v_Μ  =  2π  συν(5π/6)  συν10πt  =  2π  ( - 3^1/2 / 2 )  συν10πt  =  - π 3^1/2  συν10πt   

  η μέγιστη ταχύτητα του σημείου Μ είναι :  π 3^1/2 m/s

7.     Σε γραμμικό ελαστικό μέσο μεγάλου μήκους το οποίο ταυτίζεται με τον άξονα x′Ox διαδίδονται δύο εγκάρσια αρμονικά κύματα ίδιας συχνότητας και ίδιου πλάτους.  Τα κύματα διαδίδονται προς αντίθετη κατεύθυνση και συμβάλλοντας δημιουργούν στάσιμο κύμα το οποίο έχει εξίσωση                   y(x,t)  =  0,2· συν(4πx)· ημ(10πt) (S.I.).  Το καθένα από τα τρέχοντα κύματα εξαναγκάζει το υλικό σημείο που βρίσκεται στην αρχή O(x = 0)  του άξονα να εκτελεί ταλάντωση με εξίσωση απομάκρυνσης της μορφής  y = Αημωt.
α.  Να γράψετε τις εξισώσεις των δύο αρμονικών κυμάτων που σχηματίζουν το στάσιμο κύμα.
β.  Να υπολογίσετε την απόσταση από την αρχή Ο ενός σημείου Κ του άξονα που είναι δεσμός, αν μεταξύ των σημείων Ο και Κ υπάρχουν 6 κοιλίες.
γ.  Να γράψετε τις εξισώσεις της ταχύτητας και της επιτάχυνσης ταλάντωσης του υλικού σημείου Ζ   (x_Ζ = 5/12 m)  σε συνάρτηση με το χρόνο.

α)   y(x,t)  =  0,2· συν(4πx)· ημ(10πt)  =  2A· συν(2πx/λ)· ημ(2πft)   

    Α = 0,1 m     f = 5 Hz   T = 0,2 s    λ = 0,5 m

   y₁ = 0,1 ημ2π(5t – 2x)   και   y₂ = 0,1 ημ2π(5t + 2x)   (S.I.)       

  η ταχύτητα των κυμάτων είναι : υ = λ/Τ = 2,5m/s

β)  κΟ   δ    κ    δ    κ   δ    κ   δ   κ    δ    κ   δ    κ    δΚ       (OK)  =  6 λ/2  +  λ/4  =  13/4 λ  =   13/8 m

γ)  y_Ζ (x,t) = 0,2 συν(4π 5/12) ημ(10πt) =  0,2 συν(5π/3) ημ(10πt) = 0,2 1/2 ημ(10πt) = 0,1 ημ(10πt)

      υ_Ζ (x,t)  =  π· συν(10πt)               α_Ζ (x,t)  =  - π² ημ(10πt)

8.  Σε χορδή ΟΑ μήκους L = 1,2 m, η οποία έχει τα δύο άκρα της ακλόνητα στερεωμένα, δημιουργείται στάσιμο κύμα που προέρχεται από τη συμβολή δύο τρεχόντων κυμάτων με μήκος κύματος λ.
α.  Να υπολογίσετε τον αριθμό των υλικών σημείων της χορδής που πάλλονται με μέγιστο πλάτος, αν δίνεται ότι το μήκος κύματος των τρεχόντων κυμάτων ισούται με λ = 0,4 m.
β.  Να σχεδιάσετε το στιγμιότυπο του κύματος τη χρονική στιγμή που η πλησιέστερη κοιλία στο αριστερό άκρο Ο της χορδής βρίσκεται στη θέση μέγιστης θετικής απομάκρυνσης.
γ.  Να υπολογίσετε κατά πόσο πρέπει να μεταβάλλουμε το μήκος κύματος των τρεχόντων κυμάτων, ώστε στη χορδή να δημιουργηθούν 8 κοιλίες.
δ.  Στην περίπτωση όπου στη χορδή δημιουργούνται 8 κοιλίες, να υπολογίσετε το μήκος κύματος του ηχητικού κύματος που δημιουργείται στον αέρα εξαιτίας της ταλάντωσης της χορδής, αν δίνεται ότι η ταχύτητα διάδοσης των τρεχόντων κυμάτων στη χορδή ισούται με υ = 127,5 m/s.
Δίνεται η ταχύτητα του ήχου στον αέρα: υηχ = 340 m/s

  αριθμός κοιλιών :  Ν  =  L / λ/2  =  1,2 / 0,2 =   6  κοιλίες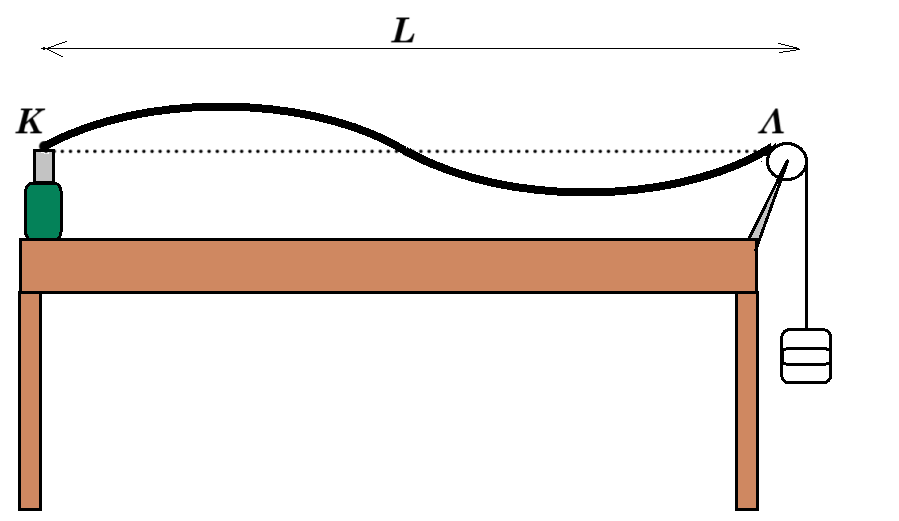 

  Ν'  =  8  κοιλίες   =>   λ'/2 =  L / Ν'  =  1,2 / 8  =>  λ' = 0,3 m   

 η συχνότητα του ηχητικού κύματος που δημιουργείται στον αέρα ισούται με τη συχνότητα ταλάντωσης των υλικών σημείων της χορδής που ταλαντώνονται  

      f  =  υ / λ'  =  υ_ηχ / λ_ηχ  =>     127,5  /  0,3   =   340  / λ_ηχ  =>  λ_ηχ  =  340 0,3 / 127,5  =  0,8 m 

....................................................................................................

ΘΕΜΑ Γ
Το άκρο Ο (x=0) μιας οριζόντιας ελαστικής χορδής αρχίζει τη χρονική στιγμή t=0 να ταλαντώνεται σύμφωνα με την εξίσωση yΟ=Aημωt.  Το εγκάρσιο αρμονικό κύμα που δημιουργείται διαδίδεται κατά μήκος του θετικού ημιάξονα Οx με ταχύτητα μέτρου υ.  Κάθε σημείο της χορδής που ταλαντώνεται κινείται μεταξύ δύο ακραίων θέσεων που απέχουν μεταξύ τους d=0,4m και η δυναμική ενέργεια της ταλάντωσής του μηδενίζεται με συχνότητα 10Hz.  Eπίσης, η οριζόντια απόσταση ενός όρους και της μεθεπόμενης κοιλάδας είναι Δx=3m.
Γ1.  Να γράψετε την εξίσωση του κύματος.
Γ2.  Για το σημείο Κ του ελαστικού μέσου (xK=3m) να βρείτε τη χρονική στιγμή που αρχίζει να ταλαντώνεται και να κάνετε τη γραφική παράσταση της επιτάχυνσής του σε συνάρτηση με το χρόνο σε αριθμημένους άξονες.
Γ3.  Δύο σημεία Μ και Ν της χορδής απέχουν μεταξύ τους οριζόντια απόσταση (ΜΝ)=5m με xN>xM. Τη χρονική στιγμή που το σημείο Ν βρίσκεται σε απομάκρυνση yN=+A για 1η  φορά, να υπολογίσετε τη φάση του σημείου Μ.
Γ4.  Αν η σημειακή μάζα του σημείου (Ο) είναι Δm=10^-6kg, να βρείτε το μέτρο του ρυθμού μεταβολής της δυναμικής ενέργειας ταλάντωσης του σημείου (Ο) τη στιγμή που η απομάκρυνσή τoυ από τη θέση ισορροπίας του είναι yo=+A/2.

Α = d/2 = 0,2 m        T/2 = 1/10Hz  =>  T = 0,2 s    ω = 2π/Τ = 2π/0,2 =  10π rad/s    

   3 λ/2 = 3 m  =>  λ = 2 m              

η ταχύτητα διαδόσεως του κύματος :   υ = λ / Τ = 2m / 0,2s = 10 m/s

  y  =  Α ημ(ωt -  2πx/λ)  =   0,2  ημ(10πt - 2πx/2)  =>  y(x,t) = 0,2 ημ(10πt - πx)

x = 3 m      t = x / v =  3 m / 10 m/s =  0,3 s      y(x=3 , t) = 0,2 ημ(10πt - 3π)   t > 0,3 s      

     v(x=3 , t)  =  2π συν(10πt - 3π)              α(x=3 , t)  =  - 20 π² ημ(10πt - 3π) 

y(x_Ν , t)  =  0,2 ημ(10πt - πx_N )   =   + 0,2   =>   ημ(10πt - πx_N )  =  +1  =  ημ(π/2) 10πt - πx_N  =  φ_Ν  =  π/2   για 1η φορά     

      y(x_M , t)  =  0,2 ημ(10πt - πx_M )         

  φ_Μ  -  φ_Ν  =   (10πt - πx_M )  -  (10πt - πx_Ν )   =   πx_Ν  -  πx_M   =   π (x_Ν  -  x_M )  =  5π  =>

  =>   φ_Μ  -  φ_Ν  =   5π  =>   φ_Μ  -  π/2  =  5π  =>  φ_Μ  =  11π/2 rad  

  y = + A/2  => ημ10πt  =  +1/2  =>   συν10πt  =  ± 3^½/2       

  y(x_ο ,t)  =  0,2 ημ10πt  =  + 0,1             υ(x_ο ,t)  =  2π συν10πt  =   ± π 3^½      

         α(x_ο ,t)  =  - 20 π² ημ10πt  =  -20 π²  ½ = - 10 π²

U  =  ½ Δm υ² =>  dU/dt = Δm v a  = 10^-6 ( ± π 3^½ ) ( -10 π² ) = ± π 3^½ 10^-4 J/s  ( π² = 10 )