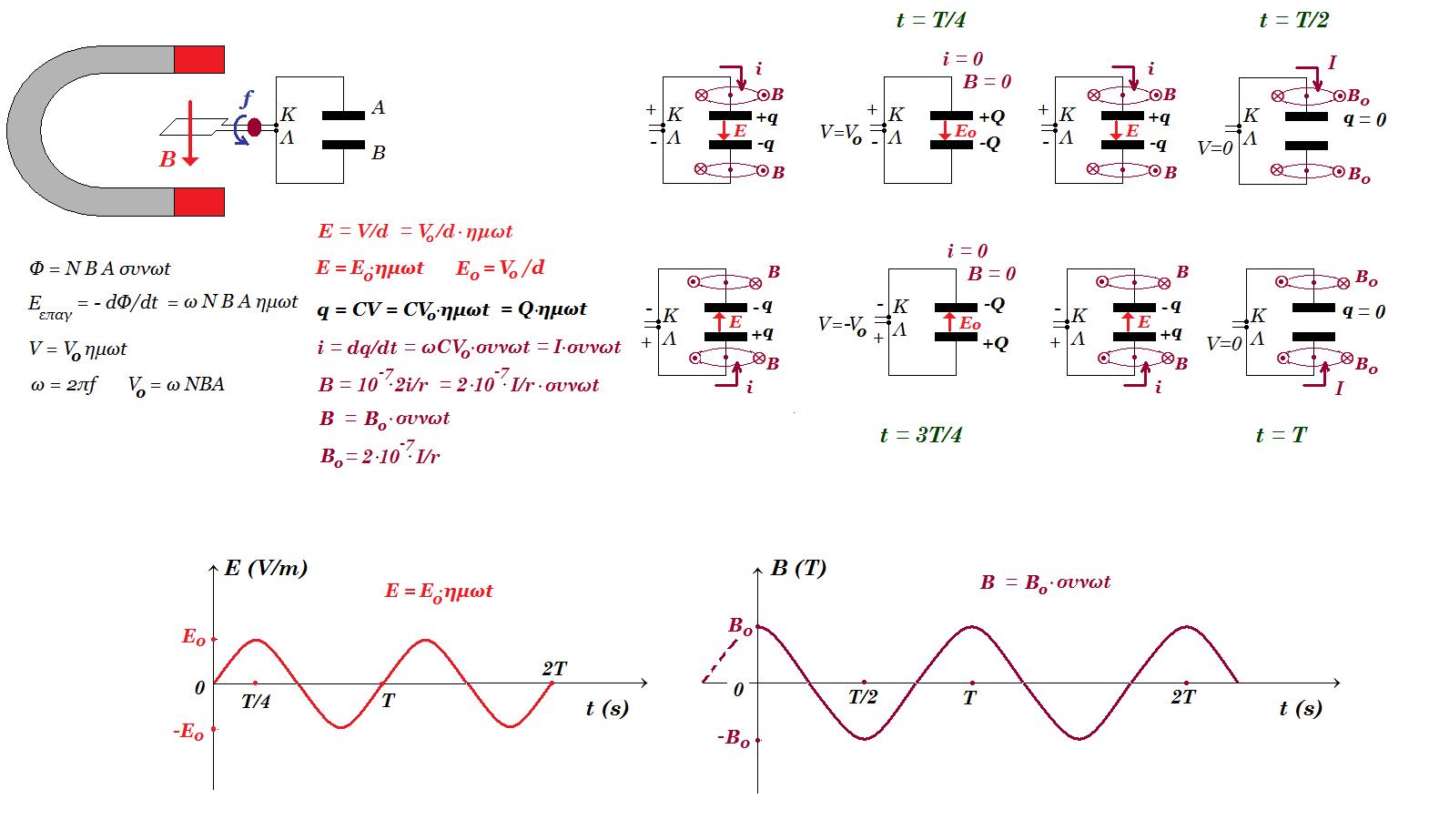
Μεταλλικό πλαίσιο μηδενικής ωμικής αντίστασης, με εμβαδόν επιφάνειας Α,  φέρει  Ν σπείρες,  στρέφεται μέσα σε ομογενές μαγνητικό πεδίο εντάσεως Β  του οποίου οι δυναμικές γραμμές είναι κάθετες στον άξονα του πλαισίου.  Αρχικά η επιφάνεια του πλαισίου είναι κάθετη στις δυναμικές γραμμές του πεδίου.  Τα άκρα Κ, Λ του πλαισίου συνδέονται με καλώδια μηδενικής ωμικής αντίστασης  με  δύo αγωγούς  Α και Β,  αφόρτιστους,  που απέχουν απόσταση d.   Περιστρέφουμε το πλαίσιο με σταθερή γωνιακή ταχύτητα  ω.  Η μαγνητική ροή που διέρχεται μέσα από την επιφάνεια του πλαισίου,  των δυναμικών γραμμών του πεδίου δίνεται από τη σχέση :  Φ =  N B A συνθ  = Ν Α Β συνωt.  ( t = 0  => συνωt = 1 => Φ =  N B A  μέγιστη ροή ).   Επειδή η γωνία θ μεταβάλλεται  με το χρόνο  τότε μεταβάλλεται η ροή Φ  και εμφανίζεται επαγωγική τάση στα άκρα  Κ  Λ  του πλαισίου.  E_επαγ = - ΔΦ/Δt  =  - dΦ/dt  =  - N B A ( συνωt )'  =  ω Ν Β Α ημωt.   Η τάση αυτή μεταβάλλεται αρμονικά ( ημιτονοειδώς ) με το χρόνο   είναι εναλλασσόμενη τάση :  V = V₀ ημωt     όπου V₀ = ω Ν Β Α   είναι η μέγιστη τάση ( πλάτος τάσης ).   Μεταξύ των αγωγών Α και Β  δημιουργείται ηλεκτρικό πεδίο με ένταση  Ε = V / d  =  V₀/d ημωt . 

Τη στιγμή t = 0 η τάση είναι μηδέν  αμέσως μετά  το άκρο Κ του πλαισίου αποκτά  έστω θετικό δυναμικό  και το άκρο Λ αποκτά αρνητικό.  Ηλεκτρόνια κινούνται από το Λ  προς τον αγωγό Β  και από τον αγωγό Α  προς το άκρο Κ.  Δημιουργείται ρεύμα  εντάσεως i  με συνέπεια μαγνητικό πεδίο.  Σε απόσταση  r  η ένταση του μαγνητικού πεδίου είναι : Β = 10^-7 2i/r .  Tη στιγμή  t=T/4   μεταξύ των άκρων Κ, Λ  επικρατεί μέγιστη τάση V₀ ,    η ένταση του ηλεκτρικού πεδίου γίνεται μέγιστη  Ε₀   και  οι αγωγοί Α , Β  αποκτούν μέγιστο φορτίο Q,   με συνέπεια το ρεύμα να μηδενίζεται.

Αμέσως μετά μειώνεται η τάση στα άκρα Κ και Λ, όχι η πολικότητα,  με συνέπεια να μειώνεται το φορτίο q  στους αγωγούς Α και Β  άρα μειώνεται η τάση στους αγωγούς Α και Β  άρα μειώνεται η ένταση Ε του ηλεκτρικού πεδίου,  τα καλώδια διαρρέονται από ρεύμα έντασης  i   ίδιας φοράς   μέχρι τη στιγμή   t=T/2  όπου μηδενίζεται η τάση μεταξύ των άκρων Κ, Λ  άρα  μηδενίζεται το φορτίο  άρα μηδενίζεται η ένταση του ηλεκτρικού πεδίου,  ενώ  η ένταση του ρεύματος γίνεται  Ι  μέγιστη   με συνέπεια η ένταση του μαγνητικού πεδίου να γίνεται μέγιστη Β₀ .      

Αμέσως μετά αλλάζει η πολικότητα των άκρων Κ και Λ  ( το Κ φορτίζεται αρνητικά  και το Λ θετικά )  τα ηλεκτρόνια κινούνται από το άκρο Κ προς τον αγωγό Α  και από τον αγωγό Β  προς το άκρο Λ  ( δηλαδή κινούνται αντίθετα απ' ότι προηγουμένως ),  αυξάνεται η τάση,   αυξάνεται το φορτίο,   αυξάνεται η τάση μεταξύ των αγωγών Α, Β   συνεπώς αυξάνεται  η ένταση  Ε  του ηλεκτρικού πεδίου μεταξύ των αγωγών Α, Β  ( έχει αντίθετη κατεύθυνση απ' ότι προηγουμένως ) ,  επειδή τα ηλεκτρόνια κινούνται αντίθετα απ' ότι προηγουμένως  η φορά του ρεύματος είναι αντίθετη απ' ότι προηγουμένως και συνεχώς μειώνεται η ένταση του  i   συνεπώς μειώνεται η ένταση Β  του μαγνητικού πεδίου ( η φορά είναι αντίθετη απ' ότι προηγουμένως )  μέχρι τη  t=3T/4  όπου μεταξύ των άκρων Κ, Λ  επικρατεί μέγιστη τάση  -V₀  και  οι αγωγοί Α , Β  αποκτούν μέγιστο φορτίο Q, η ένταση του ηλεκτρικού πεδίου γίνεται μέγιστη  -Ε₀  με συνέπεια το ρεύμα να μηδενίζεται  καθώς και η ένταση του μαγνητικού πεδίου.

Αμέσως μετά μειώνεται η τάση στα άκρα Κ και Λ, όχι η πολικότητα,  με συνέπεια να μειώνεται το φορτίο q  στους αγωγούς Α και Β  άρα μειώνεται η τάση στους αγωγούς Α και Β  άρα μειώνεται η ένταση Ε του ηλεκτρικού πεδίου,  τα καλώδια διαρρέονται από ρεύμα  ίδιας φοράς  αυξάνεται η ένταση  i   μέχρι τη στιγμή   t=T  όπου μηδενίζεται η τάση μεταξύ των άκρων Κ, Λ  άρα  μηδενίζεται το φορτίο  άρα μηδενίζεται η ένταση του ηλεκτρικού πεδίου,  ενώ  η ένταση του ρεύματος γίνεται  Ι  μέγιστη   με συνέπεια η ένταση του μαγνητικού πεδίου να γίνεται μέγιστη Β₀ .      

ΠΡΌΒΛΗΜΑ

Μεταλλικός καθρέπτης Κ  συνδέεται στο ελεύθερο άκρο ελατηρίου και μπορεί να ταλαντώνεται σε οριζόντιο επίπεδο. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε ακλόνητο σημείο.  Ο καθρέπτης εκτελεί αρμονικές ταλαντώσεις με εξίσωση απομάκρυνσης  x = 2,2 ημt  (S.I.)  Ο μεταλλικός καθρέπτης μπορεί να λειτουργήσει και σαν ανακλαστήρας ηλεκτρομαγνητικών κυμάτων,  τα οποία εκπέμπονται από πηγή που είναι τοποθετημένη στο σημείο Π.  Στο σημείο Σ  υπάρχει δέκτης κυμάτων  και  τα κύματα μπορούν να φθάσουν σε αυτόν  είτε απευθείας  από την πηγή Π,  είτε από ανάκλαση στον καθρέπτη Κ.  Οι ταλαντώσεις του καθρέπτη γίνονται επάνω στην μεσοκάθετο ΚΜ  του τμήματος ΠΣ.  Τη χρονική στιγμή  t₀ = 0  ο καθρέπτης βρίσκεται σε απόσταση  r = 3 m  από την πηγή Π  και στο σημείο Σ  παρατηρείται ενισχυτική συμβολή. 

(α)  Να βρείτε ποια είναι η επόμενη χρονική στιγμή κατά την οποία παρατηρείται και πάλι ενισχυτική συμβολή στο σημείο Σ. 

(β)  Να γράψετε την εξίσωση  της έντασης του μαγνητικού πεδίου για το Η/Μ κύμα.

Δίνονται η απόσταση  (ΠΣ) = 2 m = 2 (ΠΜ) ,  η συχνότητα του κύματος f = 1,5 10⁸ Hz ,  η μέγιστη ένταση του ηλεκτρικού πεδίου  E₀ = 300 V/m.  Θεωρείστε ότι η θετική κατεύθυνση ταλάντωσης είναι οριζόντια προς τα δεξιά  και  2^½  = 1,4     3^½  = 1,7.

(ΠΣ) = 2 m = 2 (ΠΜ)        x = 2,2 ημt        t₀ = 0     r = 3 m    

    f = 1,5 10⁸ Hz    E₀ = 300 V/m         B₀ = ;         c = 3 10⁸ m/s 

x = 2,2 ημt =>  Α = 2,2 m  πλάτος ταλάντωσης του καθρέπτη   &   ω = 2π/Τ = 1 rad/s  =>  Τ = 2π s  χρόνου περιόδου

c = λ f  =>  λ = c / f  =  (3 10⁸ m/s)  /  (1,5 10⁸ Hz)  =  2 m   μήκος κύματος

Ε₀  =  c B₀  =>   B₀  =  E₀ / c  =  300 V/m /  3 10⁸ m/s =  10^-6  Tesla

          x = 2,2 ημt             υ  = 2,2 συνt          α = - 2,2 ημt

τη στιγμή  t₀ = 0    είναι  x = 2,2 ημt = 0    &    υ = 2,2 m/s > 0 

       ο καθρέτης είναι στην Θ.Ι. του    και   αρχίζει να κινείται οριζόντια προς τα δεξιά

(ΠΚΣ) - (ΠΣ) = Ν λ  =>   6 m  -  2 m = Ν 2 m  =>   Ν = 2  

(ΚΜ)² = (ΠΚ)² - (ΠΜ)²  =  3² - 1² = 8  =>  (ΚΜ) = 8^½ m = 2 2^½ m  = 2,8 m 

 ο καθρέπτης κινείται προς τα δεξιά  συνεπώς η απόσταση  ΚΜ  μειώνεται  κατά  x

t = ;     x =  (ΚΜ) - (ΚΜ)'  =>  2,2 ημt =  2,8 m  -  (ΚΜ)'    

(ΠΚΣ)' - (ΠΣ)' = (Ν-1) λ   =>    2 (ΠΚ)'  -  2 m =  2 m   =>  (ΠΚ)' = 2 m 

(ΚΜ)' ² = (ΠΚ)' ² - (ΠΜ)' ²  =  2² - 1² = 3  =>  (ΚΜ)' = 3^½ m = 1,7 m

 οπότε  2,2 ημt = (ΚΜ) - (ΚΜ)'   =>  2,2 ημt =  2,8  -  1,7   =>   ημt = 1,1 / 2,2 =  0,5  =  ημ(π/6)  =>  t = π/6 s  

γενικά έχουμε ενισχυτική συμβολή όταν :  (ΠΚΣ) - (ΠΣ) = Ν λ  =>  2 (ΠΚ)  -  2 m =  Ν 2 m   =>  (ΠΚ) = (Ν + 1) m

 τότε  (ΚΜ)² = (ΠΚ)² - (ΠΜ)²  =  (Ν + 1)² - 1² = Ν (Ν + 2) 

Ν=0  (ΚΜ)=0 ,      Ν=1  (ΚΜ )=3^½ m = 1,732 m ,     N=2  (KM)=8^½ m = 2,828 m ,    N=3  (KM)=15^½ m = 3,873 m ,     N=4  (KM)=24^½ m = 4,9 m  , ...

ισχύει :  x(t) + (KM)_N  = 8^½ m =  (KM)_N=2  =>   2,2 ημt  +  (N² + 2N)^½   =  8^½  

ο καθρέπης εκτελεί ταλαντώσεις από τη θέση  x = - A = - 2,2 m   

 όταν   2,2 ημt = -2,2  =>   ημt = -1 = ημ(3π/2)  =>  t = 2πΚ + 3π/2   όπου  Κ = 0, 1, 2, 3, ...

 μέχρι τη θέση  x = + A = + 2,2 m   

 όταν   2,2 ημt = +2,2  =>   ημt = +1 = ημ(π/2)  =>  t = 2πΚ + π/2   όπου  Κ = 0, 1, 2, 3, ...

          πρέπει   - 2,2 m  < x(t) <  + 2,2 m  =>   - 2,2 m  <   8^½  -  (N² + 2N)^½   <  + 2,2 m  =>  

     =>   - 2,2   -  2,8  <    - (N² + 2N)^½   <  + 2,2  -  2,8   =>   - 5  <    - (N² + 2N)^½   <  - 0,6   =>  

    =>   0,6  <   (N² + 2N)^½   <  5   =>     0,36  <   N² + 2N   <  25   =>    Ν =  1,  2,  3,  4    ενισχυτική συμβολή

γενικά έχουμε  απόσβεση  όταν :  (ΠΚΣ) - (ΠΣ) = Ν λ + λ/2 =>  2 (ΠΚ)  -  2 m =  Ν 2 + 1 m  =>  (ΠΚ) = (Ν + 1,5) m

 τότε  (ΚΜ)² = (ΠΚ)² - (ΠΜ)²  =  (Ν + 1,5)² - 1² = (Ν + 0,5) (Ν + 2,5) = Ν² + 3Ν + 1,25       

  Ν=0   (ΚΜ)=1,25^½ m = 1,118 m ,       Ν=1   (ΚΜ )=5,25^½ m = 2,29 m ,       N=2   (KM)=11,25^½ m = 3,354 m ,      N=3  (KM)=19,25^½ m = 4,3875 m ,    ...

ισχύει :  x(t) + (KM)_N  = 8^½ m =  (KM)_N=2  =>   2,2 ημt  +  (N² + 3N + 1,25)^½   =  8^½  

ο καθρέπης εκτελεί ταλαντώσεις από τη θέση  x = - A = - 2,2 m   

 όταν   2,2 ημt = -2,2  =>   ημt = -1 = ημ(3π/2)  =>  t = 2πΚ + 3π/2   όπου  Κ = 0, 1, 2, 3, ...

 μέχρι τη θέση  x = + A = + 2,2 m   

 όταν   2,2 ημt = +2,2  =>   ημt = +1 = ημ(π/2)  =>  t = 2πΚ + π/2   όπου  Κ = 0, 1, 2, 3, ...

          πρέπει   - 2,2 m  < x(t) <  + 2,2 m  =>   - 2,2 m  <   8^½  -  (N² + 3N + 1,25)^½   <  + 2,2 m  =>  

    =>   - 2,2   -  2,8  <    - (N² + 3N + 1,25)^½   <  + 2,2  -  2,8   =>   - 5  <   - (N² + 3N + 1,25)^½  <  - 0,6   =>  

    =>   0,6  <   (N² + 3N + 1,25)^½  <  5   =>    0,36  <   N² + 3N + 1,25   <  25   =>   Ν =  0,  1,  2,  3   απόσβεση

 εξίσωση της έντασης του ηλεκτρικού πεδίου     Ε(x,t)  =  E₀   ημ 2π( ft - x/λ )  =  300  ημ 2π( 10⁸ t  -  x/2 )      (S.I.) 

 εξίσωση της έντασης του μαγνητικού πεδίου   Β(x,t)  =  B₀  ημ 2π( ft - x/λ )  =  10^-6  ημ 2π( 10⁸ t  -  x/2 )    (S.I.) 

                            ............................................................................................................................

Πηγή μικροκυμάτων εκπέμπει μπροστά από κατακόρυφο ανακλαστήρα. Τα κύματα συχνότητας  f=10¹⁰Ηz  προσπίπτουν κάθετα στον ανακλαστήρα, ανακλώνται χωρίς απώλειες ενέργειας ή άλλη αλλοίωση και συμβάλλουν με τα προσπίπτοντα. Δέκτης μικροκυμάτων που κινείται πάνω στη νοητή ευθεία που συνδέει πηγή και ανακλαστήρα καταγράφει μηδενική ένταση όταν είναι σε επαφή με τον τοίχο και στη συνέχεια 10 ακόμα μηδενισμούς, για μετατόπιση κατά διάστημα d. Δίνεται η ταχύτητα των κυμάτων c=3·10⁸m/s. 

(α)   Να βρεθεί η απόσταση d.

(β)  Αν για τη λήψη του κύματος αυτού απαιτείται κύκλωμα LC με πυκνωτή C=0,25pF, να υπολογιστεί ο συντελεστής αυτεπαγωγής του πηνίου L. Δίνεται π²=10

      δ    κ   δ   κ   δ   κ   δ   κ   δ   κ   δ    κ   δ   κ   δ   κ   δ   κ   δ   κ   δ   κ    

     1    1                                                                                           11          

       d  =  10 λ/2  =  5 λ  =  5 c / f  =  5 (3 10⁸ m/s)  /  (10¹⁰ Hz)  =  0,15 m                 

πρέπει    ω²  =  4π² · f² = 1 / L·C  =>   L  =  1 /  (4π² · f² · C)  =  1  /  ( 4 ·10· 10²⁰ · 0,25·10^-12 )  =  10^-9 Η

                            ............................................................................................................................

Ηλεκτρομαγνητικό κύμα συχνότητας f ταξιδεύει στον αέρα με ταχύτητα  c = 3·10⁸ m/s  προσπίπτει σε κατακόρυφο τοίχο και ανακλάται χωρίς απώλειες ενέργειας.  Έτσι σχηματίζεται στάσιμο κύμα με δεσμό στον τοίχο. Η πρώτη από το εμπόδιο κοιλία απέχει από τον τέταρτο από τον τοίχο δεσμό, απόσταση d=5·10^-2m και το πλάτος της έντασης του μαγνητικού πεδίου είναι  Β₀=8·10^-7Τ.
α. Να βρεθεί η συχνότητα της ακτινοβολίας.
β. Να γραφούν οι εξισώσεις ως προς x και t που περιγράφουν τις εντάσεις ηλεκτρικού και
μαγνητικού πεδίου.

      δ    κ   δ   κ   δ   κ   δ   κ   δ   κ      

     1    1                       4                    λ/4  +  λ/2  +  λ/2  =  d = 5·10^-2m  =>  5λ/4 = 5·10^-2m  =>  λ = 4·10^-2m

  c = λ f  => f = c / λ  =  (3·10⁸ m/s)  /  (4·10^-2m)   =  0,75·10¹⁰ Hz   =  75·10⁸ Hz  

 Ε₀  =  c B₀  =>   Ε₀  =  3·10⁸ m/s  ·  8·10^-7Τ  =  240 V/m  

 εξίσωση της έντασης του ηλεκτρικού πεδίου     Ε(x,t)  =  E₀  ημ 2π( ft - x/λ )  =  240 · ημ 2π( 75·10⁸ t  -  25x )      (S.I.) 

 εξίσωση της έντασης του μαγνητικού πεδίου   Β(x,t)  =  B₀  ημ 2π( ft - x/λ )  =  8·10^-7 · ημ 2π( 75·10⁸ t  -  25x )    (S.I.) 

                            ............................................................................................................................

H εξίσωση που περιγράφει την ένταση του ηλεκτρικού πεδίου σε ένα ηλεκτρομαγνητικό κύμα είναι, Ε(x,t)=0,03ημ(2π·10¹⁵t - 2π·10⁷x/3) (SI).
α.  Να γραφεί η εξίσωση που περιγράφει την ένταση του μαγνητικού πεδίου.
β.  Να εξεταστεί αν το κύμα αυτό ανήκει στην ορατή περιοχή του φάσματος
γ.  Να υπολογιστεί η διαφορά φάσης Δφ μεταξύ δύο σημείων που απέχουν μεταξύ τους απόσταση
Δx=4,5·10^-7m, την ίδια χρονική στιγμή.
δ.  Να βρεθεί η απόσταση x που έχει φτάσει το κύμα τη χρονική στιγμή, t=500s.
ε.  Να σχεδιαστεί το στιγμιότυπο του ηλεκτρικού κύματος τη χρονική στιγμή t=2·10^-15s.

εξίσωση της έντασης του ηλεκτρικού πεδίου   Ε(x,t)  =  E₀  ημ 2π( ft - x/λ )  =  0,03· ημ 2π(10¹⁵ t  - 10⁷ x/3 )    (S.I.) 

     λ  =  3·10^-7m  =  300 nm  < 400 nm  υπεριώδης ακτινοβολία     

    f  = 10¹⁵ Hz                 c = λ  f  = 3·10^-7m 10¹⁵ Hz =  3·10⁸ m/s 

        B₀  =  Ε₀ / c  =>   Β₀  =  0,03 V/m  /  3·10⁸ m/s  =  10^-10 Τ   

 εξίσωση της έντασης του μαγνητικού πεδίου   Β(x,t)  =  B₀  ημ 2π( ft - x/λ )  =  10^-10· ημ 2π(10¹⁵ t  - 10⁷ x/3 )   (S.I.) 

       Δφ / 2π  =  Δx / λ  =>  Δφ  =  2π  4,5·10^-7m /  3·10^-7m  =  3π rad

      x  =  c t  =  3·10⁸ m/s  500 s  =  15·10¹⁰ m

t=2·10^-15s      Ε(x) =  0,03· ημ 2π(10¹⁵·2·10^-15 - 10⁷ x/3 ) =  0,03· ημ 2π( 2 - 10⁷ x/3 )  =  0,03· ημ (4π - 2π·10⁷·x/3) 

                            ............................................................................................................................