Θετικά φορτισμένο σωματίδιο μάζας m και φορτίου q, κινείται με ταχύτητα υ πάνω σε λείο οριζόντιο επίπεδο. Καθώς κινείται στην περιοχή I του επιπέδου, εισέρχεται στην περιοχή II όπου υπάρχει περιορισμένο ένα ομογενές μαγνητικό πεδίο. Η ένταση του πεδίου είναι κατακόρυφη και η φορά της είναι από τη σελίδα προς τον αναγνώστη, όπως φαίνεται στο σχήμα.

Η περιοχή II είναι ένα ορθογώνιο παραλληλόγραμμα ΓΔΕΖ με αρκετά μεγάλο μήκος και πλάτος D. Η ταχύτητα του σωματιδίου σχηματίζει γωνία θ με την κάθετη στο μήκος ΓΔ της ορθογώνιας περιοχής II, τέτοια ώστε 0°≤θ<90°.

Εάν θ=0°,

Α.        να αποδείξετε ότι για να εξέλθει το σωματίδιο από την πλευρά ΖΕ του ορθογωνίου στην περιοχή III, πρέπει για το μέτρο της ταχύτητάς του να ισχύει ότι υ>DBq/m.

Για υ>DBq/m,

Β.        να προσδιορίσετε τη μικρότερη τιμή του μέτρου της γωνίας θ για την οποία το σωματίδιο δεν εξέρχεται στην περιοχή III, αλλά επιστρέφει στην περιοχή I.

Να αγνοήσετε τριβές, αντιστάσεις και την αλληλεπίδραση του σωματιδίου με το βαρυτικό πεδίο.

το φορτισμένο σωματίδιο εισέρχεται κάθετα (θ = 0°)  στο ομογενές μαγνητικό πεδίο    R = mv / Bq  >  D  =>  v  >  DBq / m 

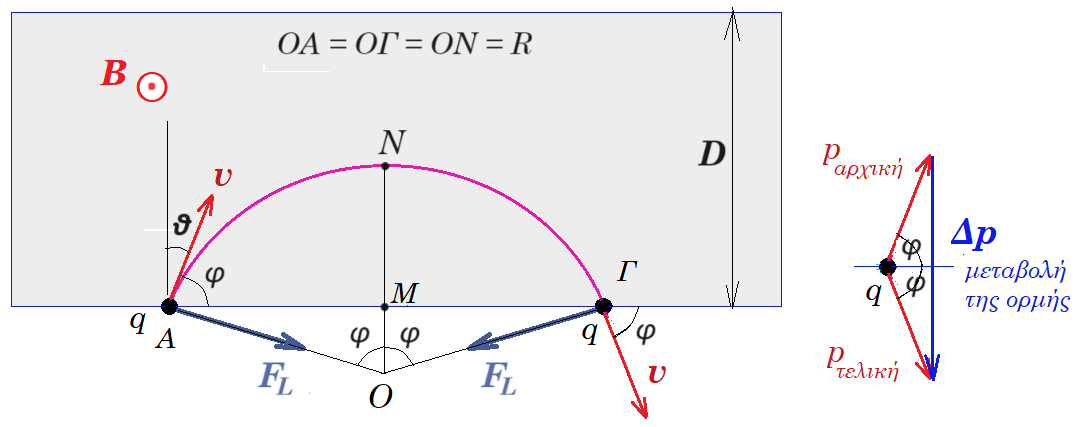
αν  v > DBq / m  =>  1 > DBq / mv              R = mv / Bq          πρέπει    MN < D  =>  R  -  R συνφ  <  D  =>  R  -  R ημθ  <  D  =>  (R  - D) / R  <   ημθ  =>  ημθ  >  1 - D/R  =>  ημθ > 1 - D / (mv/Bq)  =>  ημθ > 1 -  DBq / mv    

 q V = 0,5 m₁ v_0,1²        q V = 0,5 m₂ v_0,2²         v_0,2 = E/B = 10³ / √5∙10^-3  = √5/5∙10⁶ m/s  

 L = v_0,2 t₂  =>  t₂ = L/v_0,2          L/2 = 0,5 a₂ t₂² =  0,5 a₂ ( L/v_0,2 )² =>  a₂ = v_0,2² / L = 10¹²/5 / 0,2 =>  a₂ = 10¹² m/s²  

  a₂ = F/m₂ =>  m₂ = F/a₂  = q E / a₂  = 1,6∙10^-19  10³  /  10¹²  =>  m₂ = 1,6∙10^-28 kg             

  L = v_0,1 t₁  =>  t₁ = L/v_0,1          L/2 = 0,5 a₁ t₁² =  0,5 a₁ ( L/v_0,1 )² =>  a₁ = v_0,1² / L   

R₂ ²  =  L² + (R₂ - L/2)²  =>  R₂ ²  =  L² + R₂ ² + L²/4  -  R₂ L  =>  0  =  5L²/4  -  R₂ L  =>   R₂ = 5L/4  =  5/4 0,2 m =>  R₂ = 0,25 m  

  R₂ = m₂ v_0,2 / Bq  =>  m₂  =  R₂ Bq / v_0,2  = 0,25  √5∙10^-3  1,6∙10^-19  / √5/5∙10⁶  =  2∙10^-28 kg  

 q V = 0,5 m₂ v_0,2²  =>  V = 0,5 m₂ v_0,2² / q  = 0,5 ∙ 2∙10^-28 ∙ 10¹²/5 / 1,6∙10^-19  =  100 Volt

 R₁ ²  =  (L - d)² + (R₁ - L/2)²  =>  R₁ ²  =  15² + (R₁ - 10)²  =>  R₁ ²  =  15² + R₁ ² + 100  - 20 R₁  =>  0  =  225  + 100  - 20 R₁  =>   R₁  =  325/20  =  16,25 cm  =  0,1625 m    

  R₁ = m₁ v_0,1 / Bq  =>  m₁  =  R₁ Bq / v_0,1  = 0,1625  √5∙10^-3  1,6∙10^-19  /   =  kg  

Μονοσθενή ιόντα ισοτόπου στοιχείου εξέρχονται με μηδενική ταχύτητα από μια πηγή ιόντων τους, επιταχύνονται από τάση V, και κατόπιν εισέρχονται στο χώρο του επιλογέα ταχυτήτων διαστάσεων LxL από το μέσο Ο της πλευράς εισόδου. Τότε τα βαρύτερα ιόντα δεν εκτρέπονται και εξέρχονται από τον επιλογέα ταχυτήτων.
Αν καταργήσουμε το μαγνητικό πεδίο Β , τότε εξέρχονται όλα τα ισότοπα από το άκρο Γ του αρνητικού οπλισμού του πυκνωτή, ενώ αν καταργηθεί το ηλεκτρικό πεδίο Ε , τότε τα βαρύτερα ιόντα προσπίπτουν στο άκρο Α του θετικού οπλισμού, ενώ τα ελαφρύτερα προσπίπτουν σε σημείο Δ που απέχει απόσταση d από το Α.
Δίνονται: L=0,2m ,  E=10³ V/m,  B=√5∙10^-3 T,  q=e=1,6∙10^-19 C,   d=5cm .  Να μη ληφθεί υπόψη το βάρος των ιόντων.
1.   Υπολογίστε την μάζα m₂ των βαρύτερων ισοτόπων.
2.   Υπολογίστε την τάση V
3.   Υπολογίστε την μάζα m₁ των ελαφρύτερων ισοτόπων.
4.   Αποδείξτε ότι αν καταργηθεί το μαγνητικό πεδίο , τα ιόντα διαγράφουν την ίδια τροχιά από το Ο έως το Γ, και εξέρχονται με διαφορά χρόνου ΔtE την οποία να υπολογίσετε.
5.   Υπολογίστε τη διαφορά χρόνου κίνησης των ιόντων αν καταργηθεί το ηλεκτρικό πεδίο. Δίνονται ημ0,3π=0,8 και ημ0,37π=0,92
6.   Πόσο πρέπει να μεταβάλλουμε το ηλεκτρικό πεδίο ώστε τα ελαφρύτερα ιόντα να εξέρχονται από τον επιλογέα ταχυτήτων ακολουθώντας ευθύγραμμη πορεία.

1.   Φορτισμένο σωματίδιο αφήνεται χωρίς αρχική ταχύτητα μέσα σε ομογενές μαγνητικό πεδίο. Τι κίνηση θα κάνει;                                                                                                     θα παραμείνει στη θέση του

2.   Ηλεκτρόνιο βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο και δεν δέχεται απ' αυτό καμμία δύναμη.  Τι μπορούμε να συμπεράνουμε για την κίνηση του ηλεκτρονίου;               είτε έχει ταχύτητα μηδέν  είτε κινείται παράλληλα προ τιςδυναμικές γραμμές του πεδίου

3.   Θετικά φορτισμένο σωματίδιο εκτοξεύεται στο εσωτερικό σωληνοειδούς παράλληλα στον άξονά του.  Το σωληνοειδές έχει άπειρο μήκος και διαρρέεται από συνεχές ρεύμα σταθερής έντασης.  Τι κίνηση θα κάνει το σωματίδιο;              θα κινειθεί παράλληλα προς τις δυναμικές γραμμές δηλαδή  παράλληλα προς τον άξονα

4.   Πως μπορούμε να αλλάξουμε την τροχιά ενός ηλεκτρονίου  χωρίς να μεταβληθεί η κινητική του ενέργεια;                      να εκτοξευθεί με ταχύτητα μέσα σε ομογενές μαγνητικό πεδίο  όχι  παράλληλα προς τις δυναμικές του γραμμές

5.   Πρωτόνιο p⁺  κινείται μέσα σε ομογενές μαγνητικό πεδίο σε κυκλική τροχιά.  Πόση κινητική ενέργεια πρέπει να έχει ένα σωματίδιο α  ώστε μέσα στο ίδιο μαγνητικό πεδίο να κινείται σε κυκλική τροχιά ίσης ακτίνας;  Δίνονται οι σχέσεις :  m_a = 4m_p ,  q_a = 2q_p         

      R = m_p v_p / q_p B  =  m_a v_a / q_a B  =>  R = m_p v_p / q_p B  =  4m_p v_a / 2q_p B  =>  v_p  =  2v_a  

       E_p = 0,5 m_p v_p²     E_a = 0,5 m_a v_a²  = 0,5 4m_p v_p²/4   =  E_p          το σωματίδιο  α  έχει την ίδια κινητική ενέργεια με το πρωτόνιο

6.   Δύο πρωτόνια  Α  και  Β  εισέρχονται κάθετα προς τις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου με ταχύτητες μέτρου  υ  και  2υ  αντίστοιχα.  Βρείτε την σχέση :  α)  των ακτίνων των κύκλων που διαγράφουν,    β)  των περιόδων της κυκλικής κκίνησής τους,   γ)  των κινητικών τους ενεργειών όταν έχουν διαγράψει μισό κύκλο.  R = m_p v_p / q_p B     Τ = 2π m_p / q_pB    E_p = 0,5 m_p v_p²    R_Β = 2R_Α ,  Τ_Β = Τ_Α , Ε_Β = 4Ε_Α   

7.   Δύο θετικά φορτισμένα σωματίδια εισέρχονται με την ίδια ταχύτητα υ₀  κάθετα προς στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου.  Αν τα σωματίδια διαγράφουν την ίδια τροχιά ποιά από τις επόμενες προτάσεις είναι λανθασμένη;

    α)  έχουν την ίδια μάζα  και  το ίδιο φορτίο                                                                              σωστή

    β)  έχουν το ίδιο ειδικό φορτίο  q/m.                                                                                          σωστή

8.   Φορτισμένο σωματίδιο εισέρχεται σε ομογενές μαγνητικό πεδίο κάθετα προς στις δυναμικές γραμμές του πεδίου.   Ποιά από τις επόμενες προτάσεις είναι λανθασμένη;

      α)  η κινητική ενέργεια του σωματιδίου παραμένει σταθερή                                             σωστή

      β)  η ορμή του σωματιδίου παραμένει σταθερή                                                                                   λάθος

      γ)  το έργο της δύναμης Laplace  μέσα  σε χρόνο  t = Τ/4  είναι μηδέν.                            σωστή

9.    Δέσμη πρωτονίων εισέρχεται με ταχύτητα  υ₀  σε ομογενές μαγνητικό πεδίο κάθετα προς τις δυναμικές του γραμμές  και διαγράφει κύκλο ακτίνας R.  Τα ιόντα μιας δέσμης μονοσθενών ιόντων εισέρχεται με την ίδια ταχύτητα  υ₀  κάθετα στις δυναμικές γραμμές του ίδιου πεδίου  και  διαγράφουν κύκλο ακτίνας 11R.  Σε ποιό στοιχείο ανήκουν τα ιόντα της δεύτερης δέσμης;                          R_p = m_p v₀ / q_p B        R = m v₀ / q B      q = q_p = |q_e|        R = 11R_p =>   m v₀ / q B = 11 m_p v₀ / q_p B  =>  m = 11 m_p   Na  νάτριο                      

10.  Φορτισμένο σωματίδιο κινείται μέσα σε ομογενές μαγνητικό πεδίο κάθετα προς στις δυναμικές γραμμές του πεδίου.  Κάποια στιγμή το σωματίδιο διέρχεται μέσα από λεπτό μεταλλικό φύλλο  και χάνει τα  3/4  της κινητικής ενέργειας.  Να βρεθεί ο λόγος της αρχικής  και  της τελικής τροχιάς του σωματιδίου.           Ε_τελ = 1/4  Ε_αρχ  =>   υ_τελ²  =  1/4  υ_αρχ²  =>   υ_τελ = υ_αρχ/2  =>   R_τελ  =  R_αρχ/2         διότι  R = m v / q B

11.  Ηλεκτρόνιο εκτοξεύεται στο εσωτερικό σωληνοειδούς  κάθετα προς τον άξονά του.  Το σωληνοειδές έχει άπειρο μήκος και διαρρέεται από συνεχές ρεύμα σταθερής έντασης.  Τι κίνηση θα κάνει το ηλεκτρόνιο;           κυκλική κίνηση γύρω από τον άξονα  σε επίπεδο παράλληλα με τις σπείρες του πηνίου

12.  Η κοσμική ακτινοβολία που αποτελείται από φορτισμένα σωματίδια  δεν  φθάνει όλη στην επιφάνεια της γης.  Ένα μέρος από σωματίδια μικρής ενέργειας  απορροφάται  από την ατμόσφαιρα  ή  εκτρέπεται από το μαγνητικό πεδίο της γης.  Πού νομίζεται ότι φθάνει η περισσότερη ακτινοβολία στον ισημερινό  ή  στους πόλους;                                                                   στον ισημερινό  διότι το μαγνητικό πεδίο της γης είναι ασθενές   στους πόλους το μαγνητικό πεδίο της γης είναι ισχυρό

               ......................................................................................................................................

  Φορτισμένο σωματίδιο  q  μάζας m  με κινητική ενέργεια Κ κατευθύνεται προς μεταλλική επιφάνεια που είναι τοποθετημένη κάθετα στη διεύθυνση κινήσεως του.  Μπροστά από τη μεταλλική επιφάνεια υπάρχει ομογενές μαγνητικό πεδίο με τις δυναμικές του γραμμές παράλληλες στην επιφάνεια.  Το εύρος του μαγνητικού πεδίου είναι D.   Ποια είναι η ελάχιστη τιμή Β του μαγνητικού πεδίου ώστε το σωματίδιο να μην πέφτει πάνω στη μεταλλική επιφάνεια. 

όταν εισέλθει το φορτισμένο σωματίδιο στον χώρο με το μαγνητικό πεδίο  θα δεχθεί δύναμη Lorentz  κάθετη στην ταχύτητα υ  και  κάθετη στην ένταση Β  με συνέπεια να διαγράψει κυκλική τροχιά  ακτίνας R

δύναμη Lorentz = κεντρομόλος δύναη  =>  q v B  =  m v² / R  =>  R = mv / qB 

 για να μην πέσει το φορτίο πάνω στην μεταλλική επιφάνεια  πρέπει :  R < D  =>  mv / qB < D   =>  B > mv / qD

όμως ισχύει η σχέση :  K = ½ m v²  =>  v = (2K/m)^½               συνεπώς :   Β >  (2mK)^½ / qD 

               ......................................................................................................................................

  Θετικά φορτισμένο σωματίδιο  q  μάζας m  που κινείται με ταχύτητα υ = 2 10⁴ m/s  μπαίνει σε
χώρο όπου συνυπάρχουν ομογενές ηλεκτρικό και ομογενές μαγνητικό πεδίο με τις δυναμικές τους γραμμές κάθετες μεταξύ τους.  Το σωματίδιο μπαίνει κάθετα στις δυναμικές γραμμές των δυο πεδίων και  κινείται ευθύγραμμα και ομαλά.   Αν το μαγνητικό πεδίο είναι Β = 0,02 Τ  να υπολογιστεί η ένταση του ηλεκτρικού πεδίου Ε.

όταν εισέλθει το φορτισμένο σωματίδιο στον χώρο με το μαγνητικό  και  το ηλεκτρικό πεδίο  θα δεχθεί δύναμη Lorentz  F_L = q v B   κάθετη στην ταχύτητα υ  και  κάθετη στην ένταση Β    και  δύναμη Coulomb  F_C = q E   ομόρροπη της έντασης Ε του ηλεκτρικού πεδίου              

επειδή το φορτίο κινείται ευθύγραμμα ομαλά  πρέπει  α = 0  =>  ΣF = 0   άρα  οι δυνάμεις F_L , F_C   είναι αντίθετες  =>  F_L = F_C  =>  q v B  =  q E  =>  E = v B  =  2 10⁴ m/s  0,02 Tesla  =  400 Volt/m 

              ......................................................................................................................................

  Φορτισμένο σωματίδιο  q  μάζας m  που κινείται με ταχύτητα υ  μπαίνει σε χώρο όπου υπάρχει  ομογενές μαγνητικό πεδίο  κάθετα στις δυναμικές του γραμμές. Το σωματίδιο εισέρχεται στο πεδίο στο σημείο Α  και  εξέρχεται στο σημείο Γ.  Στο σημείο εισόδου Α  η ταχύτητα σχηματίζει γωνία  θ  με την ευθεία  ΑΓ.   Βρείτε τον χρόνο που κινείται το φορτίο μέσα στο μαγνητικό πεδίο,  το μήκος του ευθυγράμμου τμήματος ΑΓ  και  το μήκος του τόξου (ΑΓ).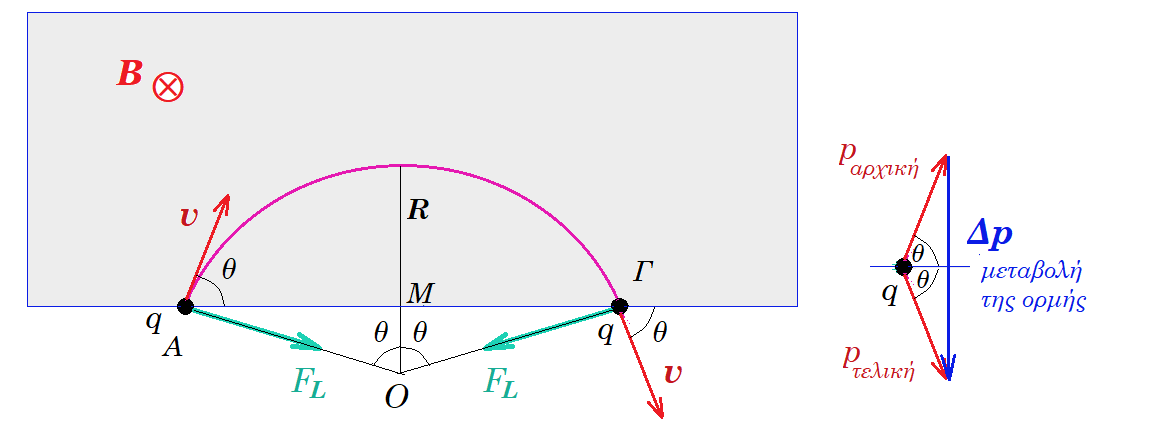

  ακτίνα κυκλικής τροχιάς :   R = mv / qB         χρόνος μιας περιόδου :  T =  2πm / qB        

έστω  Ο  το κέντρο της κυκλικής τροχιάς που διαγράφει το σωματίδιο μέσα στο ομογενές μαγνητικό πεδίο,    έχουμε  (ΟΑ) = (ΟΓ) = R ,      αν  Μ  το μέσον του ευθυγράμμου τμήματος ΑΓ     (ΜΑ) = (ΟΑ) ημθ  = R ημθ = (ΜΓ) ,    οπότε  (ΑΓ) = 2R ημθ  =  2mv ημθ / qB

το μήκος του τόξου (ΑΓ)  είναι :   2θ R  =  2θ mv / qB

σε χρόνο μιας περιόδου T  το φορτίο διανύει διάστημα  2πR,  σε χρόνο  t  διανύει τόξο (ΑΓ)   οπότε :   t  =  T 2θR /  2πR  =  T θ/π  =  ( 2πm / qB )  ( θ/π )  = 2θm / qB    

η αρχική  και η ταχύτητα  σχηματίζουν γωνία 2θ  οπότε  η μεταβολή της ορμής του σωματιδίου είναι :  Δp = 2mv ημθ

η μεταβολή της κινητικής ενέργειας του σωματιδίου  ισούται με μηδέν  διότι η ταχύτητα διατηρεί σταθερό μέτρο

              ......................................................................................................................................

  Στο χώρο μεταξύ δύο κατακόρυφων παράλληλων επιπέδων που απέχουν απόσταση d,  υπάρχει ομογενές μαγνητικό πεδίο Β με δυναμικές γραμμές παράλληλες προς τα επίπεδα αυτά.   Δέσμη φορτισμένων σωματιδίων επιταχύνεται από την ηρεμία με τάση V,  εισέρχεται στο μαγνητικό πεδίο με ταχύτητα κάθετη στο πρώτο επίπεδο.  Όταν η δέσμη εξέρχεται από το δεύτερο επίπεδο έχει εκτραπεί κατά γωνία φ  από την αρχική διεύθυνση.  Βρείτε το ειδικό φορτίο των σωματιδίων  καθώς και  τον χρόνο διέλευσης αυτών μέσα από το πεδίο.

ενέργεια σωματιδίων :   q V  =  1/2 m v²  =>   v  =  (2qV/m)^1/2    (1)

ακτίνα κυκλικής τροχιάς :   R = mv / qB    (2)     χρόνος μιας περιόδου :  T =  2πm / qB   (3)     

έστω  Ο  το κέντρο της κυκλικής τροχιάς που διαγράφει το σωματίδιο μέσα στο ομογενές μαγνητικό πεδίο,    έχουμε  (ΟΑ) = (ΟΓ) = R ,     d  =  R ημφ  =>  R  =  d / ημφ    (4) 

    (2) , (4)  =>    mv / qB  =  d / ημφ  =>   m v ημφ  =  d q B   =>   m² v² ημ²φ  =  d² q² B²   (5)

   (5) , (1)  =>  m² v² ημ²φ  =  d² q² B²  =>  m²  2qV/m  ημ²φ  =  d² q² B²    =>  m  2V  ημ²φ  =  d² q B²   =>

                =>     q/m  =  2V ( ημφ / dB )²    

σε χρόνο Τ  η δέσμη σωματιδίων διαγράφει κύκλο  2πR

σε χρόνο  t   διαγράφει τόξο   s = R φ                  

     t  =  s T / 2πR  =  R φ  T / 2πR  =  φ/2π T  =  φ/2π 2πm / qB  =  φ m / qB  =  φ / 2VB ( d B / ημφ )² =>  

                                                                                            =>    t  =  φ B d² / ( 2V/ημ²φ )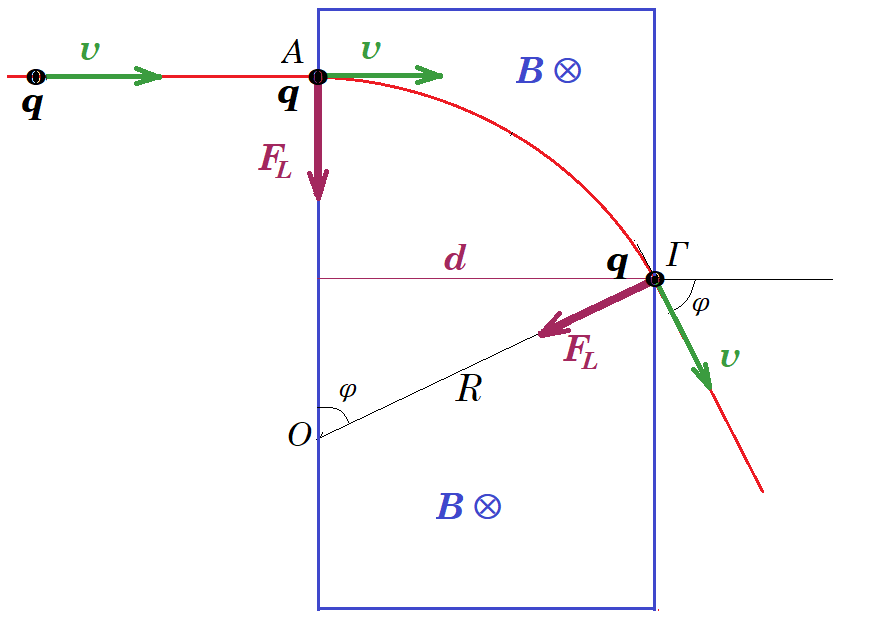   

....................................................................................................................................................

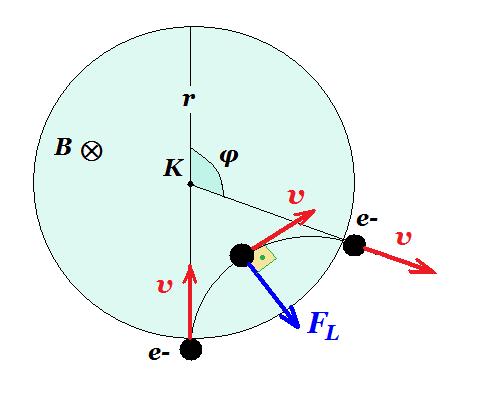Στο  σχήμα δείχνεται η εγκάρσια τομή ενός ομογενούς μαγνητικού πεδίου κυλινδρικής μορφής ακτίνας 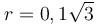m, του οποίου οι μαγνητικές γραμμές έχουν φορά από τον αναγνώστη προς τη σελίδα. Μια δέσμη ηλεκτρονίων εισέρχεται στο πεδίο με ταχύτητα μέτρου  υ=3,2·10⁶m/s  κάθετα στις δυναμικές γραμμές του, με διεύθυνση προς το κέντρο του κύκλου. Τα ηλεκτρόνια της δέσμης λόγω της μαγνητικής δύναμης που δέχονται, εξέρχονται από το πεδίο με γωνιακή εκτροπή φ=120°.
α.  Να βρείτε την ακτίνα της κυκλικής τροχιάς των σωματιδίων.
β.  Να βρείτε το μέτρο της έντασης Β του μαγνητικού πεδίου,
γ.  Να βρείτε τη διάρκεια κίνησης των ηλεκτρονίων μέσα στο μαγνητικό πεδίο.
δ.  Να βρείτε το μέτρο της μεταβολή της ορμής ενός ηλεκτρονίου κατά την κίνησή του στο μαγνητικό πεδίο.

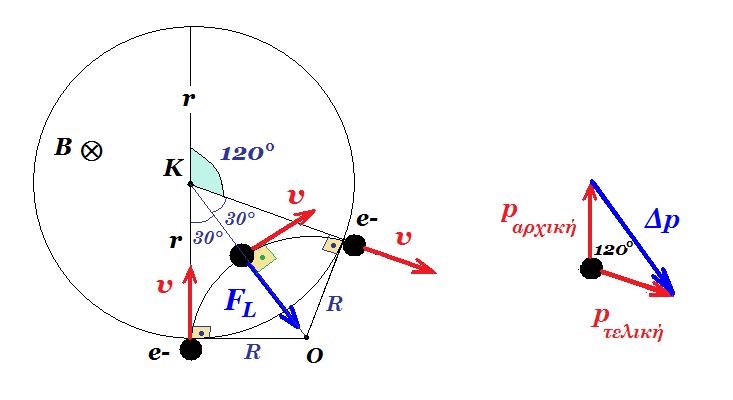  έστω Ο  το κέντρο της κυκλικής τροχιάς του ηλεκτρονίου  μέσα στο μαγνητικό πεδίο Β  και R  η ακτίνα της  από το σχήμα έχουμε :   

εφ30° = R/r  => R = r εφ30°  =  0,1ΧΦ3  Χ 1/Φ3 = 0,1 m

δύναμη  Lorentz  F_L  =  B q v   =   F_{κεντρομόλος}  =  m v² / R  =>   B = mv / Rq  =  ( 9 10^-31 kg  3,2 10⁶ m/s )  /  ( 0,1 m  1,6 10^-19 )  =>   B = 18 10^-5 T   

τα ηλεκτρόνια μέσα στο μαγνητικό πεδίο διαγράφουν τόξο  μήκους  RΧ θ = 0,1 m Χ 120°  =   0,1 m Χ 2π/3 rad  =  0,2π/3 m   = 2π/30 m  =  π/15 m   

 v = 2πR / T  =>  T  = 2πR / v  = 2π 0,1 m / 3,2 10⁶ m/s  =>  T  = π/16 10^-6 sec  

σε χρόνο  Τ = π/16 10^-6 sec   τα ηλεκτρόνια διαγράφουν τόξο  2πR = 2π 0,1 m      

σε            t ;                                                                                           π/15 m   

    t  = π/16 10^-6 sec π/15 m  / 2π 0,1 m  =>  t  = π/48 10^-6 sec  

  p_αρχική  = p_τελικη  =  m v  =  9 10^-31  3,2 10⁶  =  28,8 10^-25 kg m/s  

   Δp²  =  p_αρχική²  +  p_τελική²   -  2  p_αρχική  p_τελική  συν120°  =  3 p_αρχική²  =>   Δp  =  Φ3 p_αρχική  =  Φ3 28,8 10^-25 kg m/s

.................................................................................................................................................................................

Ένα σωληνοειδές έχει μήκος ℓ =0,5m και αποτελείται από  N = 1000 σπείρες  ακτίνας 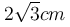. Το σωληνοειδές διαρρέεται από σταθερό ρεύμα έντασης Ι=2Α και το δημιουργούμενο μαγνητικό πεδίο το θεωρούμε ομογενές σε όλο τον εσωτερικό χώρο του πηνίου με τιμή ίση με αυτήν που έχει στο κέντρο του. Ένα θετικό φορτίο με λόγο  q/m = 0,5·10⁸ C/kg  εισέρχεται στο μαγνητικό πεδίο από τη μια άκρη του σωληνοειδούς με αρχική ταχύτητα 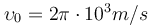, της οποίας το διάνυσμα σχηματίζει γωνία φ=60° με τον άξονα του πηνίου, όπως δείχνεται στο σχήμα.
α.  Να βρείτε την τιμή της έντασης του μαγνητικού πεδίου στο εσωτερικό του σωληνοειδούς.
β.  Να δικαιολογήσετε γιατί το σωμάτιο θα εκτελέσει ελικοειδή κίνηση και δεν θα συγκρουστεί με τα τοιχώματα του σωληνοειδούς.
γ.  Να βρείτε τον χρόνο κίνησης του σωματιδίου μέσα στο σωληνοειδές.
δ.  Να βρείτε τον αριθμό των περιφορών που θα διαγράψει το σωματίδιο μέχρι αυτό να εξέλθει από την άλλη άκρη του πηνίου.

Δίνεται μ₀=4π·10^-7 N/A².    

B = 4π·10^-7 N/A²  i N/l  = 4π·10^-7 N/A²  2· 1000 / 0,5  = 16π·10^-4  T  

 v_0x  =  v₀ συν60°  = 2π·10³ m/s  1/2  =  π·10³ m/s            v_0y  =  v₀ ημ60°  = 2π·10³ m/s Φ3/2 =  Φ3Χπ·10³ m/s        

  R = m v_0y / B q  =  m/q · v_0y/B  = 2·10^-8 kg/C· Φ3Χπ·10³ m/s  /16π·10^-4  T  =  Φ3/80 m  <  2Φ3Χ10^-2 m       1/80 < 1/50

  l = v_0x t  =>  t  =  0,5 m / π·10³ m/s  =  (1/2π)·10^-3 s  

 T = 2πR / v_0y  =  2π Φ3/80 m / Φ3Χπ·10³ m/s  =  0,25 10^-4 s   χρόνος μιας περιόδου  

  το βήμα της έλικας :   β  = v_0x Τ  = π·10³ m/s  0,25 10^-4 s  =  π/40 m   

 N  =  l / β  =  1/2 m / π/40 m =  20/π  περιφορές

.......................................................................................................................

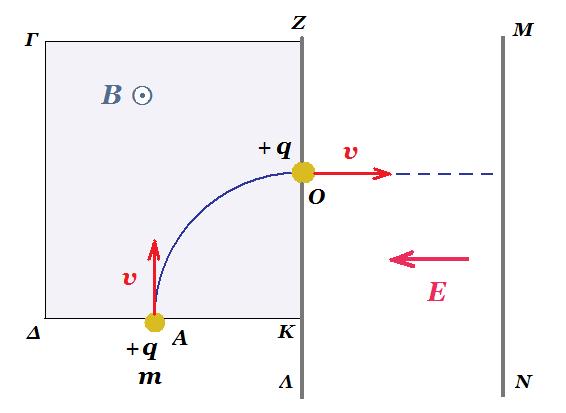
Στο σχήμα δείχνονται ένα ομογενές ηλεκτρικό και ένα ομογενές μαγνητικό πεδίο που το ένα είναι συνέχεια του άλλου. Το μαγνητικό πεδίο περιορίζεται από το ορθογώνιο ΓΖΚΔ, έχει φορά από τη σελίδα προς τον αναγνώστη και μέτρο Β=10^-2Τ. Το ηλεκτρικό πεδίο περιορίζεται από το ορθογώνιο ΖΜΝΛ, έχει φορά από τα δεξιά προς τα αριστερά και ένταση μέτρου Ε=2,5·10³Ν/C.
Ένα θετικά φορτισμένο σωματίδιο με μάζα m=1,6·10^-27 kg και φορτίο q= 1,6·10^-19C εισέρχεται στην περιοχή του μαγνητικού πεδίου με ταχύτητα μέτρου 10⁶ m/s που το διάνυσμά της είναι κάθετο στις μαγνητικές γραμμές και κάθετο στη πλευρά ΔΚ.
Το σωματίδιο αφού διαγράψει τεταρτοκύκλιο μέχρι το σημείο Ο, εξέρχεται από το μαγνητικό πεδίο και εισέρχεται στο ηλεκτρικό σε διεύθυνση παράλληλη στις ηλεκτρικές δυναμικές γραμμές του.
α.  Να βρείτε το μέτρο υ_Ο της ταχύτητας του σωματιδίου, όταν εισέρχεται στο ηλεκτρικό πεδίο.
β.  Να υπολογίσετε την ακτίνα της κυκλικής τροχιάς που διαγράφει το σωματίδιο μέσα στο μαγνητικό πεδίο.
γ.  Να υπολογίσετε τη διαφορά δυναμικού μεταξύ των πλακών ΖΛ και ΜΝ, ώστε το σωματίδιο να φθάσει με μηδενική ταχύτητα στην πλάκα ΜΝ.
δ.  Να βρεθεί ο συνολικός χρόνος κίνησης του σωματιδίου από τη στιγμή της εισόδου στο μαγνητικό πεδίο μέχρι να φθάσει στην πλάκα ΜΝ.
Η επίδραση του πεδίου βαρύτητας να θεωρηθεί αμελητέα.

 R = mv / Bq  =  ( 1,6 10^-27 10⁶ ) / ( 10^-2 1,6 10^-19 )  =  1 m  

 T  =  2πR / v  =   2π 1 / 10⁶  = 2π 10^-6 s               t₁ = T/4 = π/2 10^-6 s   

  F  =  E q = 2,5·10³Ν/C  1,6·10^-19C  = 4·10^-16 N                  a  =  F / m  = 4·10^-16 N / 1,6·10^-27  =  2,5·10¹¹ m/s²        

  v  =   v_O  -  a t  =>  0  =  10⁶  -  2,5 10¹¹ t  =>  t₂  = 4·10^-6 s     

  t_ολικό  =  t₁  +  t₂  =  (π/2 + 4)·10^-6 s          

  x  =  v_O t -  ½ a t²  =  10⁶  4·10^-6  -  ½  2,5·10¹¹  (4·10^-6 )²  =   4  - 2 = 2 m

  V  =  E x  = 2,5·10³ V/m  2 m  =  5000 V  =  V_MZ    

Ενας επιλογέας ταχυτήτων αποτελείται από δύο ομογενή πεδία, ένα ηλεκτρικό έντασης Ε=100Ν/m και ένα μαγνητικό πεδίο έντασης Β = 10^-2Τ. Τα δύο πεδία έχουν τις δυναμικές γραμμές κάθετες μεταξύ τους
Α.  Να βρείτε την ταχύτητα υ με την οποία πρέπει να κινείται ένα θετικά φορτισμένο σωματίδιο κάθετα στις δυναμικές γραμμές των πεδίων, ώστε να μην εκτρέπεται από αυτά.
Β.  Το προηγούμενο φορτισμένο σωματίδιο έχει λόγο q/m=10⁶C/kg και κινούμενο με ταχύτητα 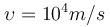εισέρχεται με τον ίδιο τρόπο στον προηγούμενο χώρο, στον οποίο τώρα υπάρχει μόνο το ηλεκτρικό πεδίο. Αν το μήκος των πλακών του πυκνωτή είναι ℓ=40cm να βρείτε:
  i.   την επιτάχυνση που αποκτά το φορτισμένο σωματίδιο εξαιτίας του ηλεκτρικού πεδίου.
  ii.  την κατακόρυφη γραμμική εκτροπή του φορτίου, όταν αυτό εξέλθει από τον πυκνωτή.

  iii.  την διαφορά δυναμικού μεταξύ των σημείων εισόδου και εξόδου από το ηλεκτρικό πεδίο του πυκνωτή.

 ΣF = 0  =>  F_E  =  F_L  =>  q E  =  B q v   =>   Ε  =  Β υ  =>  υ  =  Ε / Β =  100 / 0,01 =  10⁴ m/s

  F_E  =  q E  =  m a  =>  a  = E q / m  =  100  10⁶  =  10⁸ m/s²   

  l  =  v t  =>  t  =  l / v  =  0,4 / 10⁴  =  4 10^-5 s          

  y  =  0,5  a  t²  =  0,5   10⁸  (  4 10^-5  )²   =  8 10^-2 m  =  8 cm   =  0,08 m

  V  =  E y  =  100  0,08  =  8 Volt