|
|
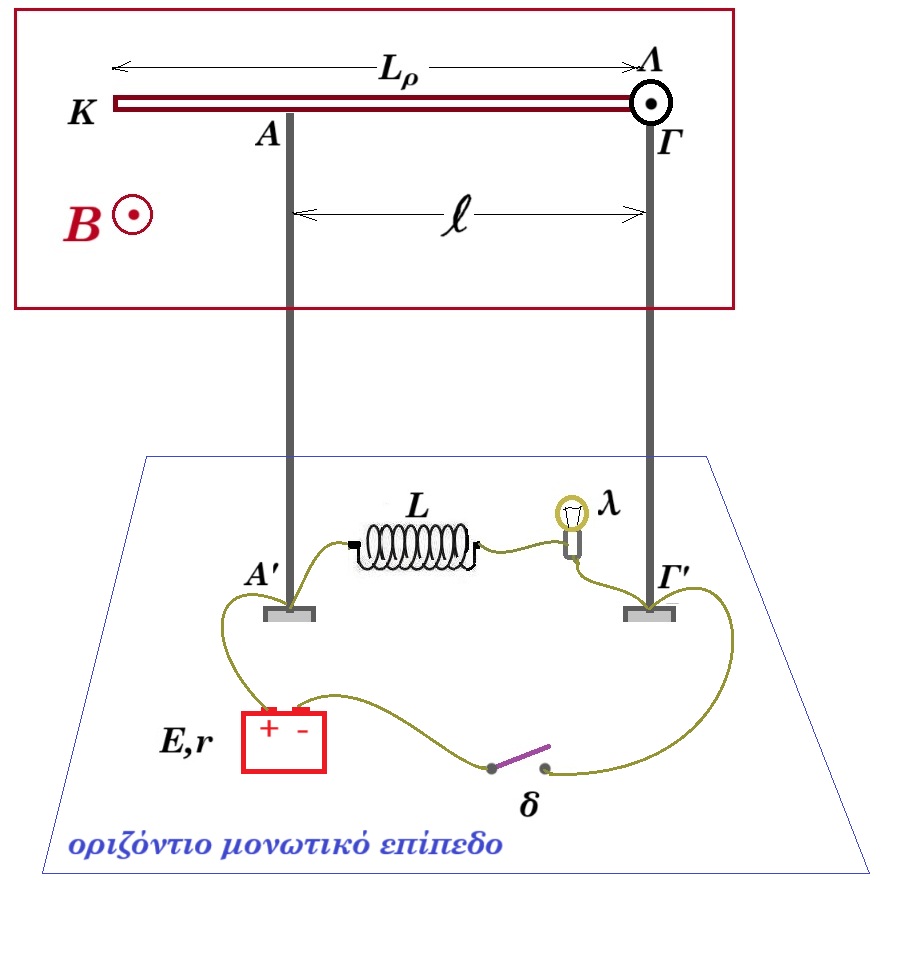
AA' // ΓΓ' αγωγοί (ΑΓ) = (Α'Γ΄) = 0,3 m στο σημείο Γ έχουμε άρθρωση όπου είναι το άκρο Λ της μεταλλικής ράβδου ΚΛ
ράβδος μεταλλική (ΚΛ) = 0,5 m RΚΛ = 10 Ω m = 0,3 kg
πηγή ρεύματος E = 12 V r = 0 B = 1 T
πηνίο ιδανικό L = 1 H λαμπτήρας ( 12 V, 48 W )
τη στιγμή t = 0 κλείνουμε τον διακόπτη
(α) να υπολογισθούν τα ρεύματα αμέσως μόλις κλείσει ο διακόπτης
(β) να υπολογισθούν τα ρεύματα μετά από αρκετό χρόνο
(γ) τη στιγμή που το ρεύμα στον κλάδο της πηγής είναι 4Α να υπολογισθεί ο ρυθμός αύξησης της ενέργειας του μαγνητικού πεδίου στο πηνίο
Αφού αποκατασταθούν τα ρεύματα ανοίγουμε τον διακόπτη χωρίς να δημιουργηθεί σπινθήρας
(δ) να βρεθεί η ελάχιστη τιμή που δέχεται η ράβδος στο σημείο επαφής Α κατά την διάρκεια του φαινομένου από τη στιγμή t = 0 και μετά
|
(α) τη στιγμή που κλείνουμε τον διακόπτη το πηνίο δεν διαρρέεται από ρεύμα ο λαμπτήρας δεν φωτοβολεί
E = i R => 12V = i 6Ω => i = 2 A η ράβδος δέχεται δύναμη Laplace FL = B l i = 1 0,3 2 = 0,6 N προς τα κάτω
ροπές ως προς Λ : Στ(Λ) = 0 => mg (ΚΛ)/2 + FL (ΑΓ)/2 + FΑ (ΑΓ) = 0 =>
=> 0,3 10 0,5/2 + 0,6 0,3/2 + FΑ 0,3 = 0 => 2,5 + 0,3 + FΑ = 0 => FA = - 2,8 N προς τα πάνω
(β) αργότερα το κύκλωμα διαρρέεται από ρεύμα η αντίσταση του λαμπτήρα Rλ = 122 / 48 = 3 Ω ρεύμα λειτουργίας του λαμπτήρα iλ = 48 / 12 = 4 Α η πηγή δίνει στο κύκλωμα ρεύμα 2Α + 4Α = 6Α
(γ) όταν η πηγή διαρρέεται από ρεύμα 4Α ο λαμτήρας και το πηνίο διαρρέονται από 4Α - 2Α = 2Α
Ε - L di/dt = i Rλ => 12 - 1 di/dt = 2 3 => di/dt = 12 - 6 = 6 A/s
dU/dt = L i di/dt = 1 2 6 = 12 J/s
(δ) όταν ανοίξουμε τον διακόπτη - L di/dt = i (Rλ + R) => - 1 di/dt = i (3 + 6) => - di/dt = 9i =>
=> di/i = - 9dt => ln(i / 4) = - 9t => i(t) = 4 e-9t (S.I.)
η αρχική τιμή του ρεύματος που διαρρέει το πηνίο είναι 4Α (δεξιά) η ράβδος διαρρέεται από 4Α (αριστερά) τότε δέχεται δύναμη Laplace FL = B l i = 1 0,3 4 = 1,2 N προς τα πάνω
ροπές ως προς Λ : Στ(Λ) = 0 => mg (ΚΛ)/2 - FL (ΑΓ)/2 + FΑ (ΑΓ) = 0 =>
=> 0,3 10 0,5/2 - 1,2 0,3/2 + FΑ 0,3 = 0 => 0,75 - 0,18 + FΑ 0,3 = 0 => FA = - 1,9 N προς τα πάνω
όταν σβήσει ο λαμπτήρας ροπές ως προς Λ : Στ(Λ) = 0 => mg (ΚΛ)/2 + FΑ (ΑΓ) = 0 => 0,3 10 0,5/2 + FΑ 0,3 = 0 => FA = - 2,5 N προς τα πάνω
Στο κύκλωμα οι λαμπτήρες Λ1, Λ2, Λ3 είναι όμοιοι. Η πηγή έχει ΗΕΔ Ε και εσωτερική αντίσταση r = 0. το πηνίο είναι ιδανικό τα καλώδια σύνδεσης δεν παρουσιάζουν αντίσταση. Την t0 = 0 κλείνουμε το διακόπτη. Τη στιγμή που ο ρυθμός αύξησης της ενέργειας του μαγνητικού πεδίου του πηνίου είναι dUL/dt = E2/4R όπου R η αντίσταση κάθε λαμπτήρα τότε:
α. Ο Λ1 φωτοβολεί πιο έντονα από τους Λ2 και Λ3 που φωτοβολούν το ίδιο.
β. Όλοι οι λαμπτήρες φωτοβολούν το ίδιο.
γ. Οι Λ2 και Λ3 φωτοβολούν το ίδιο και ο Λ1 λιγότερο από τους Λ2 και Λ3.
Όλοι οι λαμπτήρες συμπεριφέρονται ως ωμικοί αντιστάτες και η φωτοβολία είναι ανάλογη της ισχύος τους.
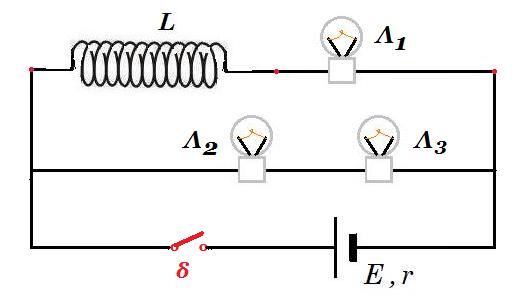
E - L di1/dt = i1 R (1) E = i2 2R => i2 = E / 2R (2) i = i1 + i2 (3)
E - L di1/dt = i1 R => - L di1/dt = i1 R - E => - L di1/dt = R ( i1 - E/R ) => di1 / ( i1 - E/R ) = - R/L dt =>
=> ln { ( i1 - E/R ) / (- E/R) } = - R/L t => ( i1 - E/R ) = (- E/R) e-R/L t => i1 (t) = E/R ( 1 - e-R/L t )
UL = 0,5 L i12 dUL / dt = L i1 di1/dt = L E/R ( 1 - e-R/L t ) E/L e-R/L t = E2 /R ( 1 - e-R/L t ) e-R/L t
dUL / dt = E2 / 4R => E2 /R ( 1 - e-R/L t ) e-R/L t = E2 / 4R => ( 1 - e-R/L t ) e-R/L t = 1/4 =>
=> e-2R/L t - e-R/L t + 1/4 = 0 Δ = 1 - 4 1/4 = 0 e-R/L t = 1/2
οπότε i1 = E/R ( 1 - e-R/L t ) = E/R ( 1 - 1/2 ) = E / 2R = i2 από σχέση (2)
dUL / dt = L i1 di1/dt => E2 / 4R = i1 ( Ε - i1 R ) => E2 / 4R = E i1 - i12 R => E2 - 4R E i1 + i12 4R2 = 0 => ( 2R i1 - E )2 = 0 => i1 = E / 2R = i2
................................................................................................................................................................
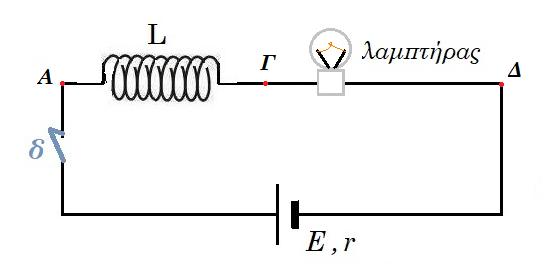
Στο κύκλωμα του σχήματος υπάρχει λαμπτήρας με αντίσταση RΛ = 1 Ω, πηγή με Η.Ε.Δ. Ε = 18 V και εσωτερική αντίσταση r = 0,5 Ω και ιδανικό πηνίο με συντελεστή αυτεπαγωγής L = 0,24 H και αριθμό σπειρών Ν = 200. Τη χρονική στιγμή t0 = 0 κλείνουμε τον διακόπτη. Όταν σταθεροποιηθεί η ένταση του ρεύματος ο λαμπτήρας λειτουργεί κανονικά.
1) Να υπολογίσετε τα στοιχεία κανονικής λειτουργίας του λαμπτήρα.
2) Να υπολογίσετε την τάση στα άκρα του λαμπτήρα όταν ο ρυθμός μεταβολής της έντασης του ρεύματος είναι ίσος με το ένα τρίτο της μεγίστης τιμής του.
Όταν σταθεροποιηθεί η ένταση του ρεύματος στο κύκλωμα ανοίγουμε τον διακόπτη, αποσυνδέουμε το πηνίο και το χωρίζουμε σε δυο νέα πηνία με το ένα να έχει αριθμό σπειρών Ν1 = 50. Συνδέουμε τα δυο πηνία με κατάλληλο τρόπο και το σύστημα τους τοποθετείται στην θέση του αρχικού πηνίου. Όταν κλείσουμε τον διακόπτη η αρχική τιμή του ρυθμού μεταβολής της έντασης που διαρρέει την πηγή είναι διαφορετική σε σχέση με την τιμή που είχε όταν κλείσαμε τον διακόπτη στο αρχικό κύκλωμα.
3) Να βρείτε τον τρόπο σύνδεσης των δυο πηνίων και την αρχική τιμή του ρυθμού μεταβολής της έντασης του ρεύματος που διαρρέει την πηγή.
4) Να βρείτε την ενέργεια που είναι αποθηκευμένη σε κάθε πηνίο όταν σταθεροποιηθούν οι τιμές τους και να σχεδιάσετε τις καμπύλες των ρευμάτων που διαρρέουν τους κλάδους του κυκλώματος σε σχέση με το χρόνο σε κοινό σύστημα αξόνων.
E = i (RΛ + r) => 18 V = i (1 Ω + 0,5 Ω) => i = 12 A
VΛ = i RΛ = 12 A 1 Ω = 12 V τάση λειτουργείας του λαμπτήρα
PΛ = VΛ i = 12 V 12 A = 144 Watt ισχύς κατανάλωσης του λαμπτήρα
Ε - L di/dt = i (RΛ + r)
αρχικά t = 0 i = 0 Ε = L di/dt => 18 = 0,24 di/dt => di/dt|max = 18 / 0,24 = 75 A/s
di/dt = 1/3 75 A/s = 25 A/s
Ε - L di/dt = i (RΛ + r) => 18 - 0,24 25 = i (1 Ω + 0,5 Ω) => i = 8 Α οπότε VΛ = i RΛ = 8 A 1 Ω = 8 V
πηνίο 1 Ν1 = 50 σπείρες L1 = 50/200 L = 1/4 0,24 H = 0,06 H Ε - L1 di1 /dt = i (RΛ + r) (1)
πηνίο 2 Ν2 = 150 σπείρες L2 = 150/200 L = 3/4 0,24 H = 0,18 H Ε - L2 di2 /dt = i (RΛ + r) (2)
αρχικά t = 0 i = 0 Ε = L1 di1 /dt => 18 = 0,06 di1 /dt => di1 /dt |max = 18 / 0,06 = 300 A/s
αρχικά t = 0 i = 0 Ε = L2 di2 /dt => 18 = 0,18 di2 /dt => di2 /dt|max = 18 / 0,18 = 100 A/s
i = i1 + i2 => di/dt = di1/dt + di2/dt = 300 + 100 = 400 A/s
(1) , (2) => L1 di1 /dt = L2 di2 /dt => L1 ( i1 - i1,0 ) / dt = L2 ( i2 - i2,0 ) / dt => L1 i1 = L2 i2 =>
=> 0,06 i1 = 0,18 i2 => i1 = 3 i2
όταν αποκατασταθεί το ρεύμα στο κύκλωμα E = i (RΛ + r) => 18 V = i (1 Ω + 0,5 Ω) => i = 12 A
i1 = 3/4 i = 9 Α i2 = 1/4 i = 3 Α
U1 = ½ L1 i12 = ½ 0,06 92 = 2,43 J U2 = ½ L2 i22 = ½ 0,18 32 = 0,81 J
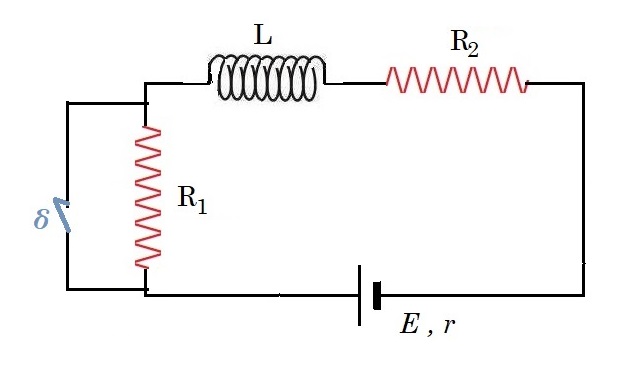 Θεωρούμε το κύκλωμα του σχήματος όπου R1 = 4Ω, R2 = 2Ω, E = 12V, r = 0, L = 0,1 H ο διακόπτης αρχικά είναι ανοικτός και τη στιγμή t = 0 κλείνουμε αυτόν.
Θεωρούμε το κύκλωμα του σχήματος όπου R1 = 4Ω, R2 = 2Ω, E = 12V, r = 0, L = 0,1 H ο διακόπτης αρχικά είναι ανοικτός και τη στιγμή t = 0 κλείνουμε αυτόν.
i) Να βρεθεί η ενέργεια που έχει αποθηκευτεί στο μαγνητικό πεδίο του πηνίου.
ii) Σε μια στιγμή t0=0 κλείνουμε το διακόπτη δ.
α) Να βρεθεί η τάση στα άκρα κάθε αντιστάτη και η τάση στα άκρα του πηνίου, αμέσως μετά το κλείσιμο του διακόπτη, καθώς και τη στιγμή t1 που η ένταση του ρεύματος έχει την τιμή i1=5Α.
β) Ποια η ισχύς της πηγής και του πηνίου τις δυο παραπάνω χρονικές στιγμές;
iii) Αφού σταθεροποιηθεί ξανά η ένταση του ρεύματος, την στιγμή t2 ανοίγουμε το διακόπτη δ. Να υπολογιστεί η ισχύς της πηγής, η ισχύς κάθε αντιστάτη και η ισχύς του πηνίου, αμέσως μετά το άνοιγμα του διακόπτη.
t = 0 E = I (R1 + R2) => 12 = I 6 => I = 2A UL = ½ L I2 = ½ 0,1 22 = 0,2 J
όταν κλείσουμε τον διακόπτη βρχυκυκλώνουμε την αντίσταση R1 οπότε μεταβάλλεται η ένταση του ρεύματος που διαρρέει το πηνίο άρα μεταβάλλεται η ένταση του μαγνητικού πεδίου στο εσωτερικό του πηνίου με συνέπεια να μεταβάλλεται η μαγνητική ροή και εμφανίζεται επαγωγική τάση στα άκρα του πηνίου E - L di/dt = Ι R2 => 12 - L di/dt = 2 2 => - L di/dt = Εαυτεπ = - 8V αντίθετη πολικότητα από την πηγή
E - L di/dt = i R2 => 12 - 0,1 di/dt = i 2 => - 0,1 di/dt = 2 (i - 6) => di / (i - 6) = - 20 dt => ln [ (i - 6) / (2 - 6) ] = - 20 t => i - 6 = - 4 e-20t => i(t) = 6 - 4 e-20t di/dt = 80 e-20t
t = 0 i = 6 - 4 = 2A t ® ¥ i = 6A
i(t) = 6 - 4 e-20t = 5A => 4 e-20t = 6 - 5 = 1 => e-20t = 1/4 => 20t = ln4 => t = 0,1 ln2 s
PL = L i di/dt = 0,1 ( 6 - 4 e-20t ) 80 e-20t = 8 e-20t ( 6 - 4 e-20t ) = 8 1/4 5 = 10 J/s
PE = E i = 12V 5A = 60 Watt PR2 = i2 R2 = 25 2 = 50 W 60 = 50 + 10
E - L di/dt = i (R1 + R2) => 12 - 0,1 di/dt = i 6 => - 0,1 di/dt = 6 (i - 2) =>
=> di / (i - 2) = - 60 dt => ln [ (i - 2) / (6 - 2) ] = - 60 t => i - 2 = 4 e-60t => i(t) = 2 + 4 e-60t
t = 0 i = 2 + 4 = 6A t ® ¥ i = 2A

Α. Για το κύκλωμα του σχήματος το πηνίο είναι ιδανικό, με συντελεστή αυτεπαγωγής L=0,2H, η πηγή έχει Ε=100V, r=2Ω και ο αντιστάτης R=8Ω. Τη χρονική στιγμή t=0 περνάμε τον μεταγωγό στη θέση A. Να υπολογίσετε:
α. την τελική τιμή Ι0 του ρευματος.
β. τη μέγιστη ενέργεια μαγνητικου πεδίου που αποθηκευτηκε στο πηνίο.
γ. τον μέγιστο ρυθμό μεταβολής της έντασης του ρεύματος.
δ. την ελάχιστη τιμή της πολικής τάσης.
Τη στιγμή που ο αντιστάτης διαρρέεται από ρεύμα ένταςης i=2Α να υπολογίσετε:
ε. την EAYT που αναπτύσσεται στο πηνίο.
στ. τον ρυθμό μεταβολής της έντασης του ρεύματος.
ζ. την πολική τάση της πηγής.
η. την ισχύ σε κάθε στοιχείο του κυκλώματος: Pπηγής, Pr, PR, PL.
E - L di/dt = i (R + r) => - 0,2 di/dt = i 10 - 100 => - 0,2 di/dt = 10 (i - 10) => di / (i - 10) = - 50 dt =>
=> ln { (i - 10) / (- 10) } = - 50 t => i - 10 = - 10 e-50t => i(t) = 10 (1 - e-50t)
i(0) = 0 αρχική τιμή του ρεύματος i(¥) = 10 Α = I0 τελική τιμή του ρεύματος
U = 0,5 L I02 = 0,5 0,2 102 = 10 Joule
di(t)/dt = 50 e-50t t=0 di/dt = 50 A/s
Vπολική = Ε - i r = 100 - 10 (1 - e-50t) 2 = 80 + 20 e-50t t = 0 Vπολική = 100 V t = ¥ Vπολική = 80 V
E - L di/dt = i (R + r) => 100 + ΕΑΥΤ = 2 10 => ΕΑΥΤ = - 80 V
ΕΑΥΤ = - L di/dt => - 80 = - 0,2 di/dt => di/dt = 400 A/s
Vπολική = Ε - i r = 100 - 2 2 = 96 V
Ρπηγής = Ε i = 100 V 2 A = 200 Watt Pr = i2 r = 22 2 = 8 W PR = i2 R = 22 8 = 32 W
PL = L i di/dt = 0,2 2 400 = 160 W 200 = 8 + 32 + 160
..........................................................................................................

Β. Για το κύκλωμα του σχήματος το πηνίο είναι ιδανικό, με συντελεστή αυτεπαγωγής L=0,1H, η πηγή έχει Ε=100V, r=1Ω και ο αντιστάτης R=9Ω. Τη χρονική στιγμή t=0 περνάμε τον μεταγωγό από τη θέση A στη θέση B. Να υπολογίσετε:
α. την αρχική τιμή Ι0 του ρεύματος.
β. τη μέγιστη ενέργεια μαγνητικου πεδίου που αποθηκεύτηκε στο πηνίο.
γ. την αρχική τιμή της τάσης από αυτεπαγωγή στο πηνίο.
δ. τον ελάχιστο ρυθμό μεταβολής της έντασης του ρεύματος.
Τη στιγμή που ο αντιστάτης διαρρέεται από ρεύμα έντασης i=5Α να υπολογίςετε:
ε. την EAYT που αναπτύσσεται στο πηνίο.
ςτ. τον ρυθμό μεταβολής της έντασης του ρεύματος.
ζ. την ισχύ σε κάθε στοιχείο του κυκλώματος: PR, PL.
E = I0 (r + R) => 100 = I0 10 => I0 = 10 A αρχική τιμή του ρεύματος
- L di/dt = i R => - 0,1 di/dt = i 9 => - 0,1 di/dt = 9 i => di / i = - 90 dt =>
=> ln (i / 10) = - 90 t => i(t) = 10 e-90t
i(0) = 10 A = I0 αρχική τιμή του ρεύματος i(¥) = 0 τελική τιμή του ρεύματος
U = 0,5 L I02 = 0,5 0,1 102 = 5 Joule
ΕΑΥΤ = - L di/dt = I0 R = 10 A 9 Ω = 90 Volt = 100 - 10 = E - I0 r
i(t) = 10 e-90t di/dt = - 900 e-90t t = 0 di/dt = - 900 A/s t = ¥ di/dt = 0
ΕΑΥΤ = - L di/dt = i R = 5 9 = 45 V di/dt = - 45 V / 0,1 H = - 450 A/s
PR = i2 R = 52 9 = 225 W PL = L i di/dt = 0,1 5 (- 450) = - 225 W
Διαθέτουμε μία πηγή συνεχούς τάσης, ένα αμπερόμετρο, ένα βολτόμετρο, δύο διακόπτες, ένα ιδανικό πηνίο (δηλαδή δεν έχει ωμική αντίσταση) με συντελεστή αυτεπαγωγής L=0,2H και αριθμό σπειρών ανά μονάδα μήκους n=40σπείρες/cm, έναν αντιστάτη αντίστασης R=6Ω και φτιάχνουμε το κύκλωμα του παρακάτω σχήματος. Τα όργανα μέτρησης θεωρούνται ιδανικά.

Αρχικά, οι διακόπτες δ1 και δ2 είναι ανοικτοί και η ένδειξη του βολτομέτρου είναι ίση με V0=20V. Κάποια στιγμή, κλείνουμε το διακόπτη δ1 (διατηρώντας τον δ2 ανοικτό) και μετά τη σταθεροποίηση του ρεύματος, η ένδειξη του αμπερομέτρου ισούται με 5A.
Α. Να υπολογίσετε την ηλεκτρεγερτική δύναμη E της πηγής και την εσωτερική της αντίσταση r.
Β. Να κατασκευάσετε τη χαρακτηριστική καμπύλη της πηγής.
Γ. Να υπολογίσετε την ένταση του μαγνητικού πεδίου στο εσωτερικό του πηνίου κατά την παραπάνω σταθεροποιημένη κατάσταση.
Κάποια χρονική στιγμή t=t1, και ενώ βρισκόμαστε στην παραπάνω σταθεροποιημένη κατάσταση, ανοίγουμε τον διακόπτη δ1 και ταυτόχρονα κλείνουμε το διακόπτη δ2.
Δ. Να υπολογίσετε τη θερμότητα που αποδίδεται στο περιβάλλον, από τη χρονική στιγμήt=t1 μέχρι να μηδενιστεί το ρεύμα στο κύκλωμα.
Ενώ το ρεύμα στο κύκλωμα έχει μηδενιστεί, κάποια χρονική στιγμή t=t2 κλείνουμε το διακόπτη δ1, διατηρώντας κλειστό και το διακόπτη δ2.
Ε. Να προσδιορίσετε τις ενδείξεις των οργάνων μέτρησης αμέσως μετά το κλείσιμο του διακόπτη δ1 (την t=t2+) και μετά από αρκετό χρόνο, όταν θα έχουν αποκατασταθεί οι τελικές τιμές.
ο διακόπτης δ1 είναι ανοικτός οπότε το βολτόμετρο μετρά την ΗΕΔ της πηγής άρα Ε = V0 = 20 V
κλείνει ο διακόπτης δ1 τότε E = I r => 20 V = 5 A . r => r = 4 Ohm
Vπολική = E - i r => Vπολική = 20 - 4 i 0 £ i £ 5 A εξίσωση ευθείας με κλίση α = - 4 V/A
B = 4π 10-7 I n = 4π 10-7 N/A2 5 A 4000 σπείρες/m = 8π 10-3 Ν/Αm = 8π 10-3 Tesla
στο πηνίο αποθηκεύεται ενέργεια UL = ½ L I2 = 0,5 0,2 H 25 A2 = 2,5 Joule
αυτή η ενέργεια καταναλώνεται στην αντίσταση R όταν ανοίξουμε τον διακόπτη δ1 και ταυτόχρονα κλείσουμε τον διακόπτη δ2
ανοίγουμε τον διακόπτη δ1 και ταυτόχρονα κλείνουμε τον διακόπτη δ2
- L di/dt = i R => di/i = - R/L dt => i(t) = I e-R/L.t => i(t) = 5 e-6/0,2.t => i(t) = 5 e-30.t
οι δύο διακόπτες είναι κλειστοί το πηνίο αντιδρά και δεν διαρρέεται από ρεύμα ( στα άκρα του πηνίου αναπτύσεται τάση εξ'επαγωγής - L di/dt )
νόμος του Ohm για κλειστό κύκλωμα E = i ( R + r ) => 20 = i ( 6 + 4 ) => i = 2 A
Vπολική = E - i r = 20 - 2 4 = 12 Volt πολική τάση πηγής
μετά από αρκετό χρόνο το πηνίο γίνεται βραχυκύκλωμα και η αντίσταση R τίθεται εκτός κυκλώματος οπότε E = i r => 20 V = i . 4 Ohm => i = 5 A
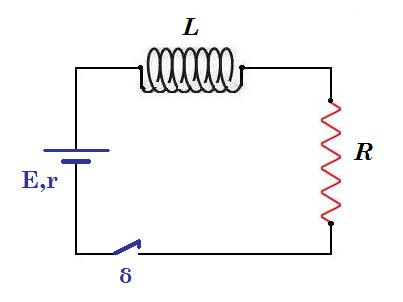 E = 40 V r = 0 R = 10 KΩ L = 0,05 H
E = 40 V r = 0 R = 10 KΩ L = 0,05 H
κλείνει ο διακόπτης δ : E - L di/dt = i R => L di/dt = E - i R = - R ( i - E/R ) =>
=> di /( i - E/R ) = - R/L dt => ln [( i - E/R ) / (- E/R )] = -R/L.t => i(t) = E/R ( 1 - e-R/L.t )
i(t) = 40/104 ( 1 - e-10000/0,05.t ) = 4 10-3 ( 1 - e-200000.t )
t = 0 i = 0 E - L di/dt = i R = 0 => di/dt = E/L = 40 / 0,05 = 800 A/s
t ® ¥ i = 4 mA
t = 3 10-6 s i = 4 10-3 ( 1 - e-200000.3 10-6 ) = 4 10-3 (1 - e-0,6) = 4 10-3 (1 - 0,55) = 4 10-3 0,45 = 1,8 10-3 A = 1,8mA
ανοίγει ο διακόπτης δ : - L di/dt = i R => L di/dt = - i R => di / i = - R/L dt => ln( i / Ι ) = -R/L.t
=> i(t) = Ι e-R/L.t Ι = 4 mA = 4 10-3 A i(t) = 4 10-3 e-10000/0,05.t = 4 10-3 e-200000.t
t = 0 i = 4 10-3 A - L di/dt = i R => di/dt = - i R/L = - 4 10-3 104 / 0,05 = - 400 A/s
t ® ¥ i = 0
..........................................................................................................................
 E = 10 V r = 0 R = 15 Ω L = 5 H η ιδανική ασφάλεια είναι των 3 Α
E = 10 V r = 0 R = 15 Ω L = 5 H η ιδανική ασφάλεια είναι των 3 Α
κλείνει ο διαόπτης δ :
το ρεύμα από την πηγή δεν διαρρέει την αντίσταση αλλά διέρχεται από την ασφάλεια και διαρρέει το πηνίο : Ε - L di/dt = 0 => 10 - 5 di/dt => di/dt = 2 A/s
το ρεύμα είναι ανάλογο του χρόνου => i = 2 t
όταν το ρεύμα γίνει 3 Α τότε t = 3/2 = 1,5 s
μετά η ασφάλεια λιώνει ( κομμένο σύρμα ) οπότε το ρεύμα από την πηγή διαρρέει την αντίσταση :
Ε - L di/dt = i R => 10 - 5 di/dt = i 15 => - 5 di/dt = 15 i - 10 => - di/dt = 3 (i - 2/3) => di / (i - 2/3) = -3 dt => ln[ (i - 2/3)/(3 - 2/3) ] = -3(t - 1,5) => (i - 2/3)/(7/3) = e-3(t - 1,5) => i(t) = 2/3 + 7/3 e-3(t - 1,5) t ³ 1,5 s di/dt = -7 e-3(t -1,5)
t = 1,5 s i = 2/3 + 7/3 = 3 A di/dt = -7 A/s
t ® ¥ i ® 2/3 A di/dt ® 0
..........................................................................................................................
 E = 12 V r = 0 R1 = 10 Ω R2 = 20 Ω L = 0,01 H
E = 12 V r = 0 R1 = 10 Ω R2 = 20 Ω L = 0,01 H
ο διακόπτης δ είναι ανοικτός, να υπολογισθούν τα ρεύματα που διαρρέουν τους κλάδους του κυκλώματος
(α) αμέσως μετά το κλείσιμο του διακόπτη δ
(β) όταν το ρεύμα που διαρρέει την μπαταρία έχει ένταση 0,5 Α
(γ) μετά από αρκετό χρόνο μετά το κλείσιμο του διακόπτη δ
κλείνει ο διακόπτης δ : i = i1 + iL L diL /dt = i1 R1 E = i R2 + i1 R1
E - L diL /dt = i R2 =>
=> E - L diL /dt = ( i1 + iL ) R2 => E - L diL /dt = ( L/R1 diL /dt + iL ) R2 =>
=> E - L diL /dt = LR2/R1 diL /dt + iL R2 => - L diL /dt - LR2/R1 diL /dt = iL R2 - E =>
=> - L ( 1 + R2/R1 ) diL /dt = R2 ( iL - E/R2 ) => diL / ( iL - E/R2 ) = - R2 / L( 1 + R2/R1 ) dt =>
=> ln[ ( iL - E/R2 )/ (- E/R2 ) ] = - R1R2 / L(R1 + R2) t => ( iL - E/R2 )/ (- E/R2 ) = e- R1R2 / L(R1 + R2) t =>
=> iL (t) = E/R2 [ 1 - e- R1R2 / L(R1 + R2) t ] iL (0) = E/R2 [ 1 - e 0 ] = 0 iL (¥) = E/R2
iL (t) = E/R2 [ 1 - e- R1R2 / L(R1 + R2) t ] => diL /dt = - E/R2 [ - R1R2 / L(R1 + R2) ] e- R1R2 / L(R1 + R2) t =>
=> diL /dt = ER1/ L(R1 + R2) e- R1R2 / L(R1 + R2) t
i1(t) = L/R1 diL /dt = E/(R1 + R2) e- R1R2 / L(R1 + R2) t
i = i1 + iL = E/(R1 + R2) e- R1R2 / L(R1 + R2) t + E/R2 [ 1 - e- R1R2 / L(R1 + R2) t ] =
= E/R2 + ( E/(R1 + R2) - E/R2 ) e- R1R2 / L(R1 + R2) t => i(t) = E/R2 - ER1 /(R1 + R2)R2 . e- R1R2 / L(R1 + R2) t
iL(t) = 12/20 [ 1 - e-200/ (0,01 30) .t ] = 0,6 [ 1 - e-2000/3 .t ]
diL /dt = ER1/ L(R1 + R2) e- R1R2 / L(R1 + R2) t = 12 10 / (0,01 30) e-200/ (0,01 30) .t = 400 e-2000/3 .t
i1(t) = 12/30 e-2000/3 t = 0,4 e-2000/3 t
i(t) = 12/20 - (12 10) / (30 20) . e-2000/3 t = 0,6 - 0,2 . e-2000/3 t = iL(t) + i1(t)
iL0) = 0,6 [ 1 - e0 ] = 0 diL /dt = 400 Α/s , iL (¥) = 0,6 A diL /dt = 0
i1(0) = 0,4 e0 = 0,4 A i1(¥) = 0
i(0) = 0,6 - 0,2 e0 = 0,6 - 0,2 = 0,4 A i(¥) = 0,6 A

i(t) = 0,6 - 0,2 . e-2000/3 t = 0,5 => 0,2 . e-2000/3 t = 0,6 - 0,5 = 0,1 => e-2000/3 t = 0,5
diL /dt = 400 e-2000/3 .t = 400 0,5 = 200 A/s
iL(t) = 0,6 [ 1 - e-2000/3 .t ] = 0,6 [ 1 - 0,5 ] = 0,3 A
i1(t) = 0,4 e-2000/3 t = 0,4 0,5 = 0,2 A
L diL /dt = i1 R1
E - L diL /dt = i R2 => 12 - 0,01 diL /dt = 0,5 20 => diL /dt = (12 - 10) / 0,01 = 200 A/s E = i R2 + i1 R1 => 12 = 0,5 20 + i1 10 => i1 = (12 - 10) / 10 = 0,2 A
i = i1 + iL => 0,5 = 0,2 + iL => iL = 0,3 A
ανοίγει ο διακόπτης δ :
- L di/dt = i R1 => L di/dt = - i R1 => di / i = - R1/L dt => ln( i / Ι ) = -R1/L.t =>
=> i(t) = Ι e-R1/L.t Ι = 0,6 A i(t) = 0,6 e-10/0,01.t = 0,6 e-1000.t
t = 0 i = 0,6 A - L di/dt = i R1 => - 0,01 di/dt = 0,6 10 => di/dt = - 600 A/s
t ® ¥ i = 0

....................................................................................................
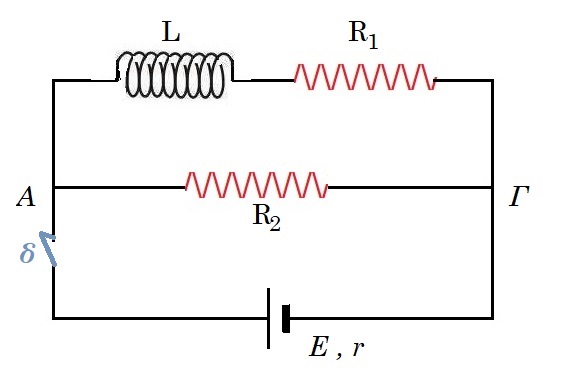 Στο κύκλωμα η μπαταρία είναι ιδανική με ΗΕΔ Ε = 10 V , r = 0 και R1 = 10 Ω, R2 = 5 Ω, L = 5 H. Κάποια στιγμή κλείνουμε τον διακόπτη. Αμέσως μετά να υπολογισθούν :
Στο κύκλωμα η μπαταρία είναι ιδανική με ΗΕΔ Ε = 10 V , r = 0 και R1 = 10 Ω, R2 = 5 Ω, L = 5 H. Κάποια στιγμή κλείνουμε τον διακόπτη. Αμέσως μετά να υπολογισθούν :
(α) τα ρεύματα που διαρρέουν τους κλάδους
(β) τη διαφορά δυναμικού στα άκρα της R1 , στα άκρα της R2 και στα άκρα του πηνίου
(γ) το ρυθμό μεταβολής του ρεύματος που διαρρέει το πηνίο.
Αρκετό χρόνο αργότερα από το κλείσιμο του διακόπτη να υπολογισθούν :
(δ) τα ρεύματα που διαρρέουν τους κλάδους
(ε) τη διαφορά δυναμικού στα άκρα της R1 , στα άκρα της R2 και στα άκρα του πηνίου
(στ) το ρυθμό μεταβολής του ρεύματος που διαρρέει το πηνίο.
Ε = i2 R2 E - L di1/dt = i1 R1 i = i1 + i2
Ε = i2 R2 => i2 = E/R2 = 10V / 5 Ω => i2 = 2 A
το πηνίο δεν διαρρέεται από ρεύμα λόγω αυτεπαγωγής i1 = 0 οπότε E - L di1/dt = 0 => di1/dt = E/L = 10 / 5 = 2 A/s
V2 = i2 R2 = E = 10 V και V1 = i1 R1 = 0
αρκετό χρόνο μετά το κλείσιμο του διακόπτη το πηνίο λειτουργεί σαν βραχυκύκλωμα οι αντιστάσεις R1 R2 συνδέονται παράλληλα R1,2 = R1 R2 / (R1 + R2 ) = 10 5 / 15 = 10/3 Ω
Ε = i2 R2 => i2 = E/R2 = 10V / 5 Ω => i2 = 2 A
Ε = i1 R1 => i1 = E/R1 = 10V / 10 Ω => i1 = 1 A di1/dt = 0 i = i1 + i2 = 3 Α
V2 = i2 R2 = E = 10 V V1 = i1 R1 = E = 10 V
.....................................................................................
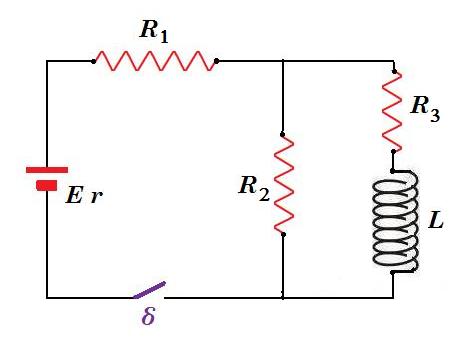
Στο κύκλωμα η μπαταρία είναι ιδανική με ΗΕΔ Ε = 10 V , r = 0 και R1 = 1 Ω, R2 = 3 Ω, R3 = 3 Ω, L = 2 H. Κάποια στιγμή κλείνουμε τον διακόπτη. Αμέσως μετά να υπολογισθούν :
(α) τα ρεύματα που διαρρέουν τους κλάδους
(β) τη διαφορά δυναμικού στα άκρα της R1 , στα άκρα της R2 , στα άκρα της R3 και στα άκρα του πηνίου
(γ) το ρυθμό μεταβολής του ρεύματος που διαρρέει το πηνίο.
Αρκετό χρόνο αργότερα από το κλείσιμο του διακόπτη να υπολογισθούν :
(δ) τα ρεύματα που διαρρέουν τους κλάδους
(ε) τη διαφορά δυναμικού στα άκρα της R1 , στα άκρα της R2 , στα άκρα της R2 και στα άκρα του πηνίου
(στ) το ρυθμό μεταβολής του ρεύματος που διαρρέει το πηνίο.
Ε = i1 R1 + i2 R2 E - L di1/dt = i1 R1 + i3 R3 i1 = i2 + i3
Ε = i2 R2 => i2 = E/R2 = 10V / 5 Ω => i2 = 2 A
το πηνίο δεν διαρρέεται από ρεύμα λόγω αυτεπαγωγής i3 = 0 οπότε i1 = i2 Ε = i1 R1 + i2 R2 = i1 ( R1 + R2 ) => i1 = i2 = E / ( R1 + R2 ) = 10 / 4 = 2,5 A
V1 = i1 R1 = 2,5A 1Ω = 2,5 V , V2 = i2 R2 = 2,5A 3Ω = 7,5 V και V3 = i3 R3 = 0
E - L di1/dt = i1 R1 => di1/dt = ( E - i1 R1 ) / L = ( 10 - 2,5 1 ) / 2 = 3,75 A/s
αρκετό χρόνο μετά το κλείσιμο του διακόπτη το πηνίο λειτουργεί σαν βραχυκύκλωμα οι αντιστάσεις R3 R2 συνδέονται παράλληλα R3,2 = R3 R2 / (R3 + R2 ) = 3 3 / 6 = 1,5 Ω η συνολική αντίσταση είναι Rολ = R1 R3,2 = 1 + 1,5 = 2,5 Ω
Ε = i1 Rολ => i1 = Ε/Rολ = 10/2,5 = 4 Α
V1 = i1 R1 = 4 1 = 4 V V2 = i1 R2,3 = 4 1,5 = 6 V = V3
i2 = V2 / R2 = 6V / 3 Ω => i2 = 2 A = i3 di3/dt = 0
η ενέργεια μαγνητικού πεδίου του πηνίου : UL = ½ L i32 = ½ 2 22 = 4 J
P1 = i12 R1 = 42 1 = 16 Watt P2 = i22 R2 = 22 3 = 12 Watt P3 = i32 R3 = 22 3 = 12 Watt
ανοίγουμε τον διακόπτη δ : L di/dt + i (R2 + R3) = 0 => L di/dt = - i (R2 + R3) => di / i = - (R2 + R3)/L dt => ln(i / i3) = - (R2 + R3)/L t => ln(i / 2) = - (3 + 3)/2 t => i(t) = 2 e-3t di/dt = -6 e-3t
dUL /dt = L i di/dt = 2 2 e-3t ( -6 e-3t ) = -24 e-6t
t = 0 dUL /dt = -24 Watt
P2 = i2 R2 = 22 e-6t 3 = 12 e-6t t = 0 P2 = 12 W
P3 = i2 R3 = 22 e-6t 3 = 12 e-6t t = 0 P3 = 12 W
η αποθηκευμένη ενέργεια στο πηνίο κατανέμεται σαν θερμότητα πάνω στις αντιστάσεις R2 και R3

Θεωρούμε τα κυκλώματα του σχήματος. Βρείτε την ένταση του ρεύματος που διαρρέει κάθε κύκλωμα
(α) αμέσως μόλις κλείσουμε τον διακόπτη δ
(β) αρκετό χρόνο μετά το κλείσιμο του διακόπτη δ
(γ) αμέσως μόλις ανοίξουμε τον διακόπτη δ
(δ) αρκετό χρόνο μετά το άνοιγμα του διακόπτη δ
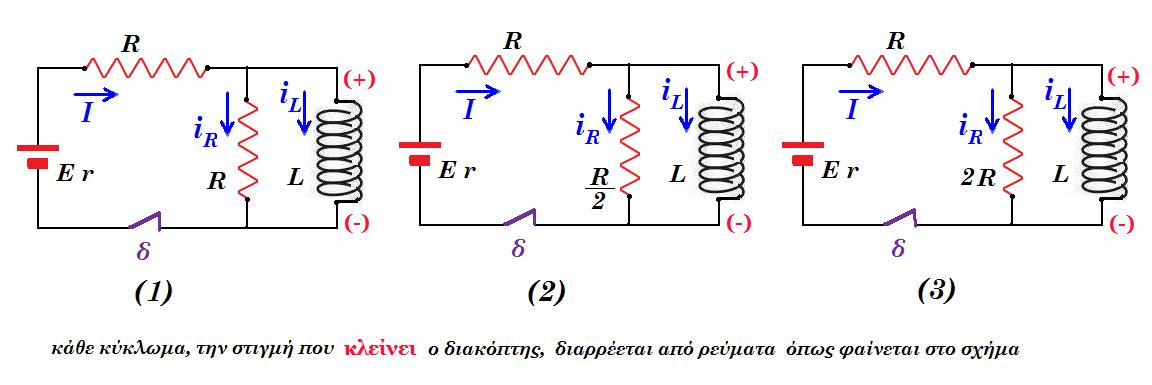
κύκλωμα (1) κλείνει ο διακόπτης :
I = iR + iL
E = I (R + r) + iR R
L diL/dt = iR R => L/R diL/dt = iR
E - L diL/dt = I (R + r) = ( iR + iL ) (R + r) = ( L/R diL/dt + iL ) (R + r) =>
=> E - L diL/dt = L diL/dt + Lr/R diL/dt + iL (R + r) =>
=> 2L diL/dt + Lr/R diL/dt = E - iL (R + r) =>
=> L(2 + r/R) diL/dt = -(R + r) [ iL - E/(R + r) ] =>
=> diL / [ iL - E/(R + r) ] = -(R + r)/ L(2 + r/R) dt =>
=> ln [ iL - E/(R + r) ] - ln [ - E/(R + r) ] = -(R + r)/ L(2 + r/R) . t =>
=> [ iL - E/(R + r) ] = [ - E/(R + r) ] . e -(R + r)/ L(2 + r/R) . t =>
=> iL (t) = E/(R + r) . [ 1 - e -(R + r)/ L(2 + r/R) . t ]
diL/dt = E/(R + r) . [ - (R+r)/ L(2+r/R) ] . [ - e -(R + r)/ L(2 + r/R) . t ] =>
=> diL/dt = ER/ L(2R+r) . e -(R + r)/ L(2 + r/R) . t
iR (t) = L/R diL/dt = E/(2R+r) . e -(R + r)/ L(2 + r/R) . t
I = iR + iL = E/(2R+r) . e -(R + r)/ L(2 + r/R) . t + E/(R + r) . [ 1 - e -(R + r)/ L(2 + r/R) . t ] =
= E/(2R+r) . e -(R + r)/ L(2 + r/R) . t + E/(R + r) - E/(R + r) . e -(R + r)/ L(2 + r/R) . t =
= E/(R + r) + [ E/(2R+r) - E/(R + r) ] . e -(R + r)/ L(2 + r/R) . t =
= E/(R + r) + E (R + r - 2R - r) / (2R+r)(R + r) . e -(R + r)/ L(2 + r/R) . t =>
I (t) = E/(R + r) - ER / (2R+r)(R + r) . e -(R + r)/ L(2 + r/R) . t
t = 0 iL (0) = E/(R + r) . [ 1 - e -(R + r)/ L(2 + r/R) . 0 ] = E/(R + r) . [ 1 - 1 ] = 0
iR (0) = E/(2R+r) . e -(R + r)/ L(2 + r/R) . 0 = E/(2R+r)
I (0) = E/(R + r) - ER / (2R+r)(R + r) . e -(R + r)/ L(2 + r/R) . 0 = E/(R + r) - ER / (2R+r)(R + r) =
= [ E(2R + r) - ER ] / (2R+r)(R + r) = E(R + r) / (2R+r)(R + r) = E / (2R+r) = iR(0)
μόλις κλείσει ο διακόπτης το πηνίο δεν διαρρέται από ρεύμα λόγω αυτεπαγωγής και η αντίσταση που συνδέεται στα άκρα του πηνίου διαρρέεται από το ρεύμα Ι = E/(2R+r)
t ® ¥ iL ® E/(R + r) . [ 1 - 0 ] = E/(R + r)
iR ® E/(2R+r) . 0 = 0
I ® E/(R + r) - ER / (2R+r)(R + r) . 0 = E/(R + r) iL = I
μετά από αρκετό χρόνο η αντίσταση που συνδέεται στα άκρα του πηνίου βραχυκυκλώνεται είναι σαν να μην υπάρχει οπότε το πηνίο διαρρέεται από το ρεύμα Ι = E/(R + r)
κύκλωμα (2) κλείνει ο διακόπτης :
I = iR + iL
E = I (R + r) + iR R/2
L diL/dt = iR R/2 => 2L/R diL/dt = iR
E - L diL/dt = I (R + r) = ( iR + iL ) (R + r) = ( 2L/R diL/dt + iL ) (R + r) =>
=> E - L diL/dt = 2L diL/dt + 2Lr/R diL/dt + iL (R + r) =>
=> 3L diL/dt + 2Lr/R diL/dt = E - iL (R + r) =>
=> L(3 + 2r/R) diL/dt = -(R + r) [ iL - E/(R + r) ] =>
=> diL / [ iL - E/(R + r) ] = -(R + r)/ L(3 + 2r/R) dt =>
=> ln [ iL - E/(R + r) ] - ln [ - E/(R + r) ] = -(R + r)/ L(3 + 2r/R) . t =>
=> [ iL - E/(R + r) ] = [ - E/(R + r) ] . e -(R + r)/ L(3 + 2r/R) . t =>
=> iL (t) = E/(R + r) . [ 1 - e -(R + r)/ L(3 + 2r/R) . t ]
diL/dt = E/(R + r) . [ - (R+r)/ L(3 + 2r/R) ] . [ - e -(R + r)/ L(3 + 2r/R) . t ] =>
=> diL/dt = ER/ L(3R + 2r) . e -(R + r)/ L(3 + 2r/R) . t
iR (t) = 2L/R diL/dt = 2E/(3R + 2r) . e -(R + r)/ L(3 + 2r/R) . t
η τάση στα άκρα της αντίστασης R/2 είναι :
V = iR R/2 = 2E/(3R + 2r) . e -(R + r)/ L(3 + 2r/R) . t R/2 = ER/(3R + 2r) . e -(R + r)/ L(3 + 2r/R) . t
κάθε αντίσταση R που συνδέεται παράλληλα στο πηνίο διαρρέεται από ρεύμα
iR' = V / R = E/(3R + 2r) . e -(R + r)/ L(3 + 2r/R) . t
I = iR + iL = 2E/(3R + 2r) . e -(R + r)/ L(3 + 2r/R) . t + E/(R + r) . [ 1 - e -(R + r)/ L(3 + 2r/R) . t ] =
= 2E/(3R + 2r) . e -(R + r)/ L(3 + 2r/R) . t + E/(R + r) - E/(R + r) . e -(R + r)/ L(3 + 2r/R) . t =
= E/(R + r) + [ 2E/(3R + 2r) - E/(R + r) ] . e -(R + r)/ L(3 + 2r/R) . t =
= E/(R + r) + E (2R + 2r - 3R - 2r) / (3R + 2r)(R + r) . e -(R + r)/ L(3 + 2r/R) . t =>
I (t) = E/(R + r) - ER / (3R + 2r)(R + r) . e -(R + r)/ L(3 + 2r/R) . t
t = 0 iL (0) = E/(R + r) . [ 1 - e -(R + r)/ L(3 + 2r/R) . 0 ] = E/(R + r) . [ 1 - 1 ] = 0
iR (0) = 2E/(3R + 2r) . e -(R + r)/ L(3 + 2r/R) . 0 = 2E/(3R + 2r) = E/(R + R/2 + r)
I (0) = E/(R + r) - ER / (3R + 2r)(R + r) . e-(R + r)/ L(3 + 2r/R) . 0 = E/(R + r) - ER / (3R + 2r)(R + r) =
= [ E(3R + 2r) - ER ] / (3R + 2r)(R + r) = 2E(R + r) / (3R + 2r)(R + r) = 2E / (3R + 2r) = iR(0)
μόλις κλείσει ο διακόπτης το πηνίο δεν διαρρέται από ρεύμα λόγω αυτεπαγωγής και η αντίσταση που συνδέεται στα άκρα του πηνίου διαρρέεται από το ρεύμα Ι = 2E/(3R + 2r)
t ® ¥ iL ® E/(R + r) . [ 1 - 0 ] = E/(R + r)
iR ® E/(2R+r) . 0 = 0
I ® E/(R + r) - ER / (3R + 2r)(R + r) . 0 = E/(R + r) iL = I
μετά από αρκετό χρόνο η αντίσταση που συνδέεται στα άκρα του πηνίου βραχυκυκλώνεται είναι σαν να μην υπάρχει οπότε το πηνίο διαρρέεται από το ρεύμα Ι = E/(R + r)
κύκλωμα (3) κλείνει ο διακόπτης :
I = iR + iL
E = I (R + r) + iR 2R
L diL/dt = iR 2R => L/2R diL/dt = iR
E - L diL/dt = I (R + r) = ( iR + iL ) (R + r) = ( L/2R diL/dt + iL ) (R + r) =>
=> E - L diL/dt = L/2 diL/dt + Lr/2R diL/dt + iL (R + r) =>
=> 3L/2 diL/dt + Lr/2R diL/dt = E - iL (R + r) =>
=> L(3/2 + r/2R) diL/dt = -(R + r) [ iL - E/(R + r) ] =>
=> diL / [ iL - E/(R + r) ] = -(R + r)/ L(3/2 + r/2R) dt =>
=> ln [ iL - E/(R + r) ] - ln [ - E/(R + r) ] = -(R + r)/ L(3/2 + r/2R) . t =>
=> [ iL - E/(R + r) ] = [ - E/(R + r) ] . e -(R + r)/ L(3/2 + r/2R) . t =>
=> iL (t) = E/(R + r) . [ 1 - e -(R + r)/ L(3/2 + r/2R) . t ]
diL/dt = E/(R + r) . [ - (R+r)/ L(3/2 + r/2R) ] . [ - e -(R + r)/ L(3/2 + r/2R) . t ] =>
=> diL/dt = 2ER/ L(3R + r) . e -(R + r)/ L(3/2 + r/2R) . t
iR (t) = L/2R diL/dt = E/(3R + r) . e -(R + r)/ L(3/2 + r/2R) . t
I = iR + iL = E/(3R+r) . e -(R + r)/ L(3/2 + r/2R) . t + E/(R + r) . [ 1 - e -(R + r)/ L(3/2 + r/2R) . t ] =
= E/(3R+r) . e -(R + r)/ L(3/2 + r/2R) . t + E/(R + r) - E/(R + r) . e -(R + r)/ L(3/2 + r/2R) . t =
= E/(R + r) + [ E/(3R+r) - E/(R + r) ] . e -(R + r)/ L(3/2 + r/2R) . t =
= E/(R + r) + E (R + r - 3R - r) / (3R + r)(R + r) . e -(R + r)/ L(3/2 + r/2R) . t =>
I (t) = E/(R + r) - 2ER / (3R + r)(R + r) . e -(R + r)/ L(2 + r/R) . t
t = 0 iL (0) = E/(R + r) . [ 1 - e -(R + r)/ L(3/2 + r/2R) . 0 ] = E/(R + r) . [ 1 - 1 ] = 0
iR (0) = E/(3R+r) . e -(R + r)/ L(3/2 + r/2R) . 0 = E/(3R+r)
I (0) = E/(R + r) - 2ER / (3R+r)(R + r) . e -(R + r)/ L(3/2 + r/2R) . 0 = E/(R + r) - 2ER / (3R + r)(R + r) =
= [ E(3R + r) - 2ER ] / (3R+r)(R + r) = E(R + r) / (3R+r)(R + r) = E / (3R+r) = iR(0)
μόλις κλείσει ο διακόπτης το πηνίο δεν διαρρέται από ρεύμα λόγω αυτεπαγωγής και η αντίσταση που συνδέεται στα άκρα του πηνίου διαρρέεται από το ρεύμα Ι = E/(3R+r)
t ® ¥ iL ® E/(R + r) . [ 1 - 0 ] = E/(R + r)
iR ® E/(3R+r) . 0 = 0
I ® E/(R + r) - 2ER / (3R+r)(R + r) . 0 = E/(R + r) iL = I
μετά από αρκετό χρόνο η αντίσταση που συνδέεται στα άκρα του πηνίου βραχυκυκλώνεται είναι σαν να μην υπάρχει οπότε το πηνίο διαρρέεται από το ρεύμα Ι = E/(R + r)
................................................................................
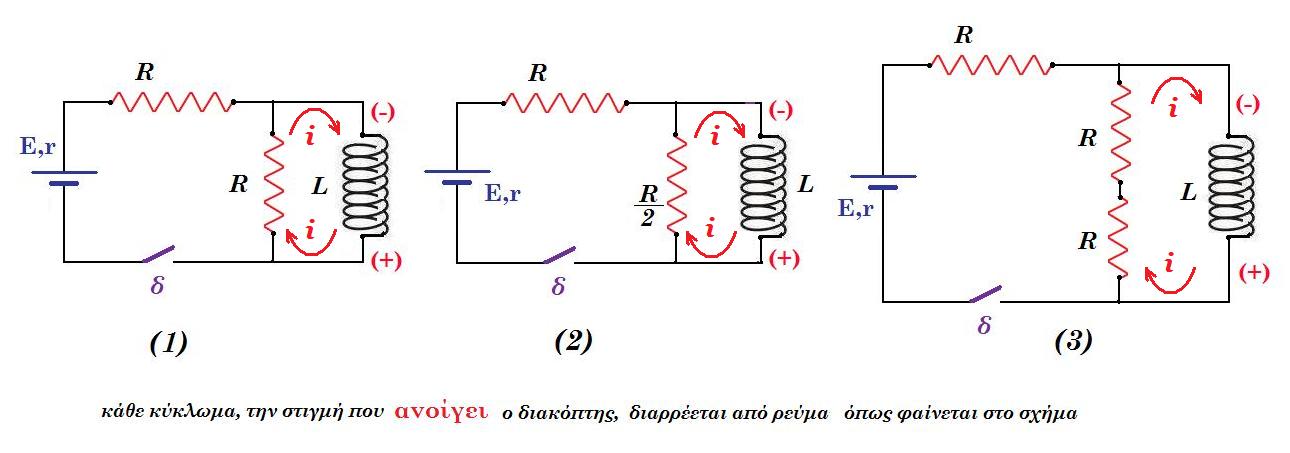
κύκλωμα (1) ανοίγει ο διακόπτης :
ο διακόπτης κλειστός πολύ χρόνο Ι = Ε / (R + r) όταν ανοίγει ο διακόπτης η πηγή τίθεται εκτός κυκλώματος και ο βρόχος που αποτελείται από το πηνίο και την αντίσταση στα άκρα του διαρρέεται από ρεύμα i
L di/dt + i R = 0 => di / i = - R/L dt => ln (i / I) = - R/L t => i(t) = I e-R/L t = Ε/(R + r) e-R/L t
κύκλωμα (2) ανοίγει ο διακόπτης :
ο διακόπτης κλειστός πολύ χρόνο Ι = Ε / (R + r) όταν ανοίγει ο διακόπτης η πηγή τίθεται εκτός κυκλώματος και ο βρόχος που αποτελείται από το πηνίο και την σύνθετη αντίσταση στα άκρα του διαρρέεται από ρεύμα i
L di/dt + i R/2 = 0 => di / i = - R/2L dt => ln (i / I) = - R/2L t => i(t) = I e-R/2L t = Ε/(R + r) e-R/2L t
κάθε παράλληλα συνδεδεμένη αντίσταση R στα άκρα του πηνίου διαρρέεται από ρεύμα iR (t) = Ε/2(R + r) e-R/2L t
κύκλωμα (3) ανοίγει ο διακόπτης :
ο διακόπτης κλειστός πολύ χρόνο Ι = Ε / (R + r) όταν ανοίγει ο διακόπτης η πηγή τίθεται εκτός κυκλώματος και ο βρόχος που αποτελείται από το πηνίο και την σύνθετη αντίσταση στα άκρα του διαρρέεται από ρεύμα i
L di/dt + i 2R = 0 => di / i = - 2R/L dt => ln (i / I) = - 2R/L t => i(t) = I e-2R/L t = Ε/(R + r) e-2R/L t
κάθε εν σειρά συνδεδεμένη αντίσταση R στα άκρα του πηνίου διαρρέεται από ρεύμα iR (t) = Ε/(R + r) e-2R/L t
.......................................................................................................................................................
Αυτεπαγωγή κλείσιμο - άνοιγμα διακόπτη
Για το κύκλωμα του σχήματος δίνονται R1=2Ω, L=0,4Η, ενώ η πηγή έχει Ε=30V και εσωτερική αντίσταση r=0 και ο διακόπτης δ κλείνει τη χρονική στιγμή t=0. Η αρχική τιμή της έντασης του ρεύματος που διαρρέει την πηγή είναι 10Α.
i) Να υπολογιστεί η αντίσταση R2 καθώς και η ισχύς που καταναλώνει μόλις κλείσουμε τον διακόπτη.
ii) Ποια η αρχική ένταση του ρεύματος που διαρρέει το πηνίο και ποιος ο αντίστοιχος ρυθμός μεταβολής της έντασης (di/dt); 
Αφού σταθεροποιηθεί η ένταση του ρεύματος που διαρρέει το πηνίο την χρονική στιγμή t1=2,5s, ανοίγουμε τον διακόπτη.
iii) Πόση θερμότητα, λόγω φαινομένου Joule παράγεται στον αντιστάτη R2 μετά το άνοιγμα του διακόπτη;
iv) Να κάνετε τη γραφική παράσταση (ποιοτικό διάγραμμα) της έντασης του ρεύματος που διαρρέει τον αντιστάτη R2 σε συνάρτηση με το χρόνο, μέχρι να μηδενιστεί η ένταση του ρεύματος που τον διαρρέει.
v) Πως μεταβάλλεται η μαγνητική ροή που διαρρέει τις σπείρες του πηνίου συναρτήσει του χρόνου καθ' όλην τη διάρκεια ;
κλείσιμο διακόπτη : Ε - L di1 /dt = i1 R1 (1) Ε = i2 R2 (2) i = i1 + i2 (3)
Ε - L di1 /dt = i1 R1 => - L di1 /dt = i1 R1 - Ε = R1 ( i - E/R1 ) => di1 / ( i - E/R1 ) = - R1/L dt =>
=> i1 (t) = E/R1 ( 1 - e - R1/L t ) i1(0) = 0 i1(¥) = E/R1
τ = L/R1 = 0,4/2 = 0,2s από τη στιγμή t = 5τ = 5 0,2s = 1s και μετά το ρεύμα που διαρρέει το πηνίο και την αντίσταση R1 σταθεροποιείται i1(¥) = E/R1 = 30 / 2 = 15 Α i1 (t) = 15 ( 1 - e -5t )
μόλις κλείσει ο διακόπτης το πηνίο δεν διαρρέεται από ρεύμα λόγω αυτεπαγωγής οπότε το ρεύμα της πηγής θα περάσει από την αντίσταση R2 από τη σχέση (2) έχουμε 30 V = 10 A R2 => R2 = 3 Ω
η ισχύς που καταναλώνεται PR2 = 102 3 = 300 Watt
από τη σχέση (1) : Ε - L di1 /dt = i1 R1 => 30V - 0,4H di1 /dt = 0 2Ω => di1 /dt = 30/0,4 = 75 Α/s
από τη στιγμή που θα κλείσουμε τον διακόπτη μέχρι να αποκατασταθούν τα ρεύματα στο κύκλωμα η αντίσταση R2=3Ω διαρρέεται από σταθερό ρεύμα i2 = 10 Α διότι συνδέεται παράλληλα στην πηγή ενώ το πηνίο και η αντίσταση R1 διαρρέονται από ρεύμα που μεταβάλλεται από 0 έως 15 Α οπότε η πηγή "στέλνει" στο κύκλωμα ρεύμα που μεταβάλλεται από 10 Α έως 25 Α τελικά οι αντιστάσεις R1 και R2 συνδέονται παράλληλα με ισοδύναμη αντίσταση R1,2 = 3Ω 2Ω / (3Ω + 2Ω) = 1,2Ω και το ρεύμα έχει ένταση i = E / R1,2 = 30V / 1,2Ω = 25 A
i1 (t) = E/R1 ( 1 - e - R1/L t ) => di1 /dt = E/R1 ( - R1/L ) ( - e - R1/L t ) = E/L e - R1/L t
Εεπαγ = - dΦ / dt => - L di1 /dt = - dΦ / dt => dΦ/dt = L E/L e - R1/L t => dΦ/dt = E e - R1/L t =>
=> dΦ = Ε e - R1/L t dt => dΦ = Ε / (- R1/L) e - R1/L t d(- R1/L)t => dΦ = - Ε L/R1 e - R1/L t d(- R1/L)t =>
ολοκληρώνουμε από t=0 Φ(0)=0 έως t=t => Φ(t) = - Ε L/R1 ( e - R1/L t - 1 ) => Φ(t) = Ε L/R1 ( 1 - e - R1/L t )
Φ(0) = 0 αρχική μαγνητική ροή Φ(¥) = Ε L/R1 μαγνητική ροή μετά την σταθεροποίηση των ρευμάτων
Φ(t) = Ε L/R1 ( 1 - e - R1/L t ) = 30 0,4 / 2 ( 1 - e - 2/0,4 t ) => Φ(t) = 6 ( 1 - e-5t )
άνοιγμα διακόπτη : - L di /dt = i ( R1 + R2 ) => di / i = - (R1 + R2)/L dt => ln ( i / I0 ) = - (R1 + R2)/L (t-2,5) => i(t) = I0 e - (R1 + R2)/L (t-2,5) όπου Ι0 = E/R1
i(t) = I0 e - (R1 + R2)/L (t-2,5) => i(t) = 15 e - (2 + 3)/0,4 (t-2,5) => i(t) = 15 e - 12,5 (t-2,5) t ³ 2,5s
τ = 1/12,5 = 0,08s από τη στιγμή t = 2,5 + 5τ = 2,5 + 5 0,08s = 2,5 + 0,4s = 2,9s και μετά το ρεύμα που διαρρέει το πηνίο και τις αντιστάσεις R1 και R2 σταθεροποιείται ( μηδενίζεται )
όταν είναι κλειστός ο διακόπτης το πηνίο διαρρέεται από ρεύμα 15 Α οπότε έχει αποθηκευμένη ενέργεια μαγνητικού πεδίου UL = 0,5 i2 L = 0,5 152 0,4 = 45 Joule
όταν ανοίξει ο διακόπτης η αποθηκευμένη ενέργεια χάνεται στις αντιστάσεις Q1 + Q2 = 45J (1)
Q1 = i2 R1 t Q2 = i2 R2 t => Q1 / Q2 = R1 / R2 = 2 / 3
(1) => 2/3 Q2 + Q2 = 45 J => 5/3 Q2 = 45 J => Q2 = 27 J
από τη στιγμή που ανοίγουμε τον διακόπτη και μετά το κύκλωμα αποτελείται από το πηνίο και τις δύο αντιστάσεις το πηνίο λόγω αυτεπαγωγής γίνεται πηγή με αντίθετη πολικότητα απ' ότι προηγουμένως και το ρεύμα μεταβάλλεται από αρχική τιμή 15 Α μέχρι να μηδενισθεί
i(t) = E/R1 e - (R1 + R2)/L (t-2,5) => di/dt = E/R1 ( - (R1 + R2)/L ) e - (R1 + R2)/L (t-2,5) = - E(R1 + R2)/R1L e - (R1 + R2)/L (t-2,5)
Εεπαγ = - dΦ / dt => - L di/dt = - dΦ / dt => dΦ/dt = L { - E(R1 + R2)/R1L } e - (R1 + R2)/L (t-2,5) =>
=> dΦ/dt = - E(R1 + R2)/R1 e - (R1 + R2)/L (t-2,5) => dΦ = - E(R1 + R2)/R1 e - (R1 + R2)/L (t-2,5) dt =>
=> dΦ = - E(R1 + R2)/R1 / { - (R1 + R2)/L } e - (R1 + R2)/L (t-2,5) d{- (R1 + R2)/L}t =>
=> dΦ = E L/R1 e - (R1 + R2)/L (t-2,5) d{- (R1 + R2)/L}(t-2,5) =>
ολοκληρώνουμε από t=2,5s Φ(2,5)=Ε L/R1 έως t=t => Φ(t) - Φ(2,5) = Ε L/R1 ( e - (R1 + R2)/L (t-2,5) - 1 ) =>
=> Φ(t) - Ε L/R1 = Ε L/R1 e - (R1 + R2)/L (t-2,5) - Ε L/R1 => Φ(t) = Ε L/R1 e - (R1 + R2)/L (t-2,5)
Φ(2,5) = Ε L/R1 αρχική μαγνητική ροή Φ(¥) = 0 τελική μαγνητική ροή
Φ(t) = Ε L/R1 e - (R1 + R2)/L (t-2,5) = 30 0,4 / 2 e - (2 + 3)/0,4 (t-2,5) => Φ(t) = 6 e-12,5 (t-2,5)


............................................................................................................................................................................
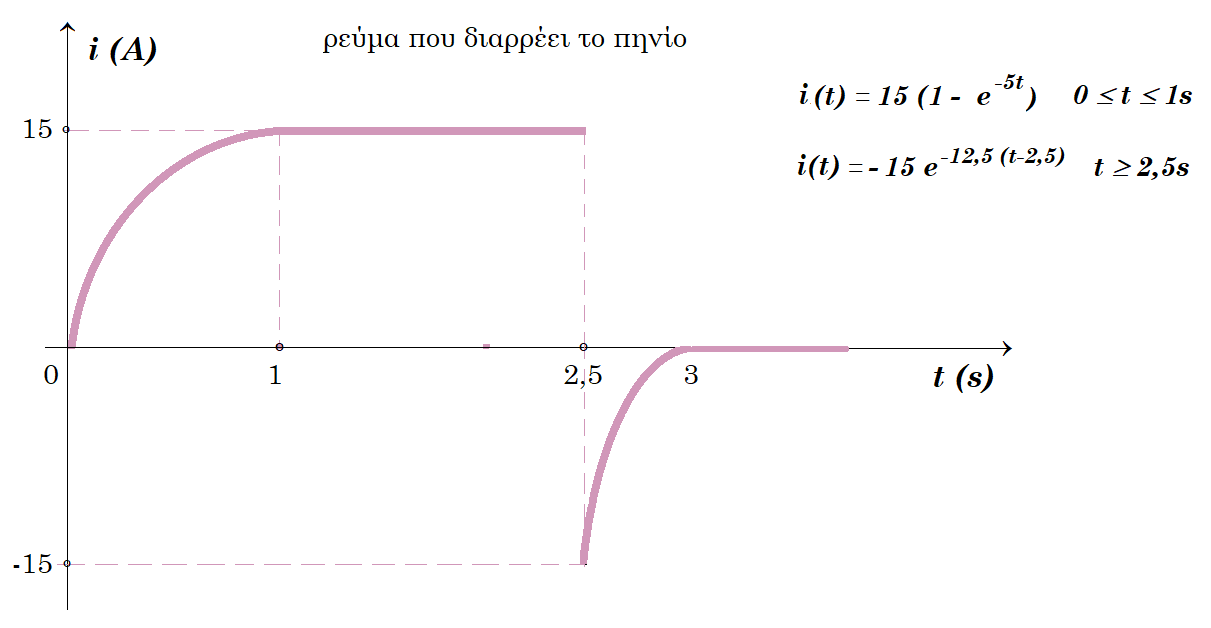
κλείνει ο διακόπτης δ1
Ε - L di/dt = i (R + r) => - L di/dt = i (R + r) - E => - L di/dt = (R + r) [ i - E/(R + r) ] =>
=> di / [ i - E/(R + r) ] = - (R + r)/L dt => ln { [ i - E/(R + r) ] / [ - E/(R + r) ] } = - (R + r)/L t =>
=> i - E/(R + r) = [ - E/(R + r) ] e- (R + r)/L t => i(t) = E/(R + r) [ 1 - e- (R + r)/L t ]
di/dt = - E/(R + r) e- (R + r)/L t { - (R + r)/L } = Ε/L e- (R + r)/L t Εαυτεπαγ(t) = - L di/dt = - Ε e- (R + r)/L t
ισχύς πηγής Ρ = Ε i => Ρ = Ε E/(R + r) [ 1 - e- (R + r)/L t ] => Ρ(t) = E2/(R + r) [ 1 - e- (R + r)/L t ]
ρυθμός αποθήκευσης ενέργειας στο πηνίο ΡL = L di/dt i = L Ε/L e- (R + r)/L t E/(R + r) [ 1 - e- (R + r)/L t ] =>
=> ΡL (t) = Ε2/(R + r) e- (R + r)/L t [ 1 - e- (R + r)/L t ]
ισχύς που καταναλώνεται στην αντίσταση R PR (t) = i(t)2 R = E2R/(R + r)2 [ 1 - e- (R + r)/L t ]2
ισχύς που καταναλώνεται στην αντίσταση r Pr (t) = i(t)2 r = E2r/(R + r)2 [ 1 - e- (R + r)/L t ]2
i(t) = E/(R + r) [ 1 - e- (R + r)/L t ] = 40/(4 + 2) [ 1 - e- (4 + 2)/0,2 t ] => i(t) = 20/3 [ 1 - e-30.t ]
5 = 20/3 ( 1 - e- 30 t ) => e- 30 t = 1/4
di/dt = - 20/3 e- (R + r)/L t (- 30) = 200 e-30.t Εαυτεπαγ(t) = - L di/dt = - 0,2 200 e-30.t = - 40 e-30.t
ισχύς πηγής Ρ = Ε i => Ρ = 40V 5A = 200 Watt
ρυθμός αποθήκευσης ενέργειας στο πηνίο ΡL = L di/dt i1 = 0,2 200 e-30t 5 => PL = 200 1/4 = 50 Watt
ισχύς που καταναλώνεται στην αντίσταση R PR = i12 R = 52 4 = 100 Watt
ισχύς που καταναλώνεται στην αντίσταση r Pr = i12 r = 52 2 = 50 Watt
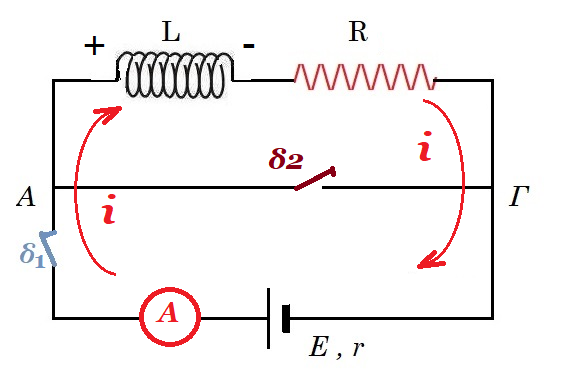
μετά το κλείσιμο του δ2
0 = L di/dt + i R => L di/dt = - i R => di / i = - R/L dt => ln i/i1 = - R/L t => i(t) = i1 e-R/L.t
di/dt = - R/L i1 e-R/L.t Εαυτεπαγ(t) = - L di/dt = R i1 e- R/L t
i(t) = i1 e-R/L.t => i(t) = 5 e-4/0,2.t => i(t) = 5 e-20.t
di/dt = -100 e-20.t Εαυτεπαγ(t) = - L di/dt = 20 e- 20 t
I = E/r = 40V / 2Ω = 20Α
I = i + i2 => i2 (t) = 20 - 5 e-20.t ρεύμα που διαρρέει τον κλάδο ΑΓ
i2 (0) = 20 - 5 e-20.0 = 20 - 5 = 15 A i(¥) = 20 Α

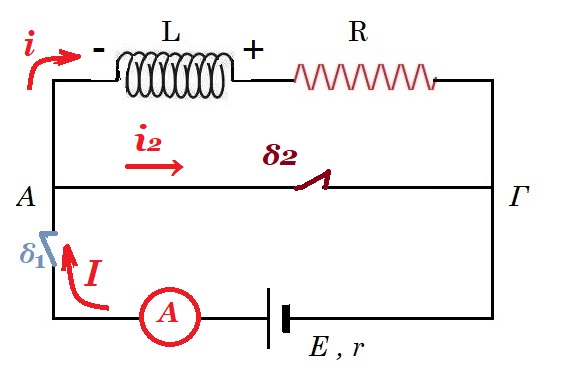
Αυτεπαγωγή άνοιγμα διακόπτη
Για το κύκλωμα του σχήματος δίνονται R1=4Ω, R2= 10Ω, L=0,2Η, ενώ η πηγή έχει Ε=20V και εσωτερική αντίσταση r=0 και ο διακόπτης δ κλείνει τη χρονική στιγμή t=0. Αφού σταθεροποιηθεί η ένταση του ρεύματος που διαρρέει το πηνίο την χρονική στιγμή t1=5s, ανοίγουμε τον διακόπτη.
α) Ποια είναι η ένταση του ρεύματος που διαρρέει κάθε κλάδο του κυκλώματος λίγο πριν το άνοιγμα του διακόπτη;
β) Βρείτε την ΗΕΔ από αυτεπαγωγή που αναπτύσσεται στο πηνίο αμέσως μετά το άνοιγμα του διακόπτη.
γ) Ποιος ο ρυθμός μεταβολής της ενέργειας του μαγνητικού πεδίου του πηνίου αμέσως μετά το άνοιγμα του διακόπτη;
δ) Να κάνετε το διάγραμμα της τάσης στα άκρα του αντιστάτη R2 (ποιοτικό διάγραμμα).
α) έστω Ι1 η ένταση του ρεύματος που διαρρέει το πηνίο όταν σταθεροποιηθεί και Ι2 η ένταση του ρεύματος που διαρρέι την αντίσταση R2 επειδή οι κλάδοι συνδέονται παράλληλα έχουμε : Ι1 = Ε / R1 = 20V / 4Ω = 5 Α και Ι2 = Ε / R2 = 20V / 10Ω = 2 Α το συνολικό ρεύμα έχει έωταση Ι = Ι1 + Ι2 = 5 + 2 = 7 Α
β) αμέσως μετά το άνοιγμα του διακόπτη στα άκρα του πηνίου αναπτύσσεται τάση από επαγωγή διότι το ρεύμα ελαττώνεται άρα ελαττώνεται η ένταση του μαγνητικού πεδίου του πηνίου άρα ελαττώνεται η μαγνητική ροή που διέρχεται μέσα από τις σπείρες του πηνίου, οπότε από τον νόμο του Ohm με αρχική τιμή Ι1 = 5 Α έχουμε : Εαυτεπαγ = I1 ( R1 + R2 ) = 5A ( 4Ω + 10Ω ) = 70 Volt το πηνίο "γίνεται" πηγή και έχουμε σε σειρά σύνδεση τις αντιστάσεις η τάση που βρίκαμε είναι αρχική μετά μειώνεται μέχρι να μηδενισθεί
από τη σχέση : Εαυτεπαγ = - L ΔΙ/Δt => 70 V = - 0,2 H (0 - 5A) / Δt => Δt = 1/70 sec
γ) ο ρυθμός μεταβολής του ρεύματος αρχικά είναι : ΔΙ/Δt = - Εαυτεπαγ / L = - 70V / 0,2H = - 350 Α/s
αρχική ενέργεια του μαγνητικού πεδίου του πηνίου : UL = 0,5 L I2 = 0,5 0,2 52 = 2,5 Joule
ο ρυθμός μεταβολής της ενέργειας του μαγνητικού πεδίου του πηνίου :
dUL / dt = L I dI/dt = 0,2H 5A ( -70V / 0,2H ) = - 350 J/s
δ) VΑΓ = E = 20 Volt πριν το άνοιγμα του διακόπτη
όταν ανοίξει ο διακόπτης έχουμε :
Eαυτεπαγ = - L di/dt = i ( R1 + R2 ) => di/dt = - i ( R1 + R2 )/L => di/i = - ( R1 + R2 )/L dt =>
=> ln (i / I1) = - ( R1 + R2 )/L t => i(t) = I1 e-( R1 + R2 )/L t το ρεύμα i έχει την φορά του Ι1
VΑΓ (t) = - VΓΑ (t) = - i(t) R2 = - I1 R2 e-( R1 + R2 )/L t = - 5 10 e-14/0,2 t => VΑΓ (t) = - 50 e-70 t 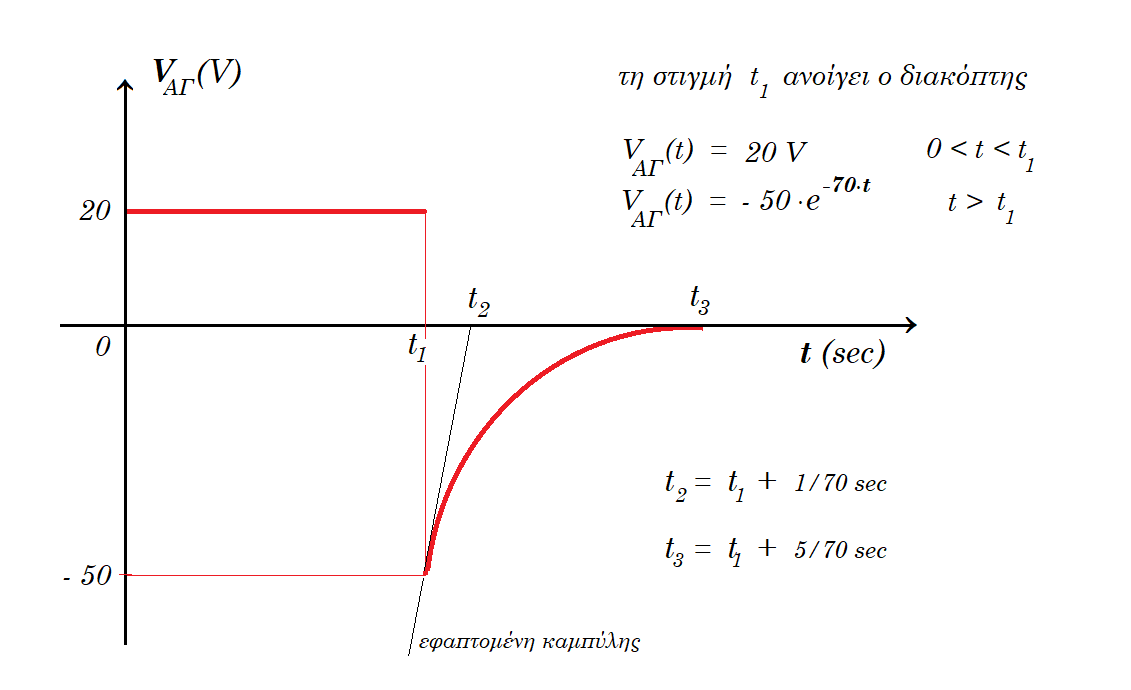
Αυτεπαγωγή κλείσιμο διακόπτη
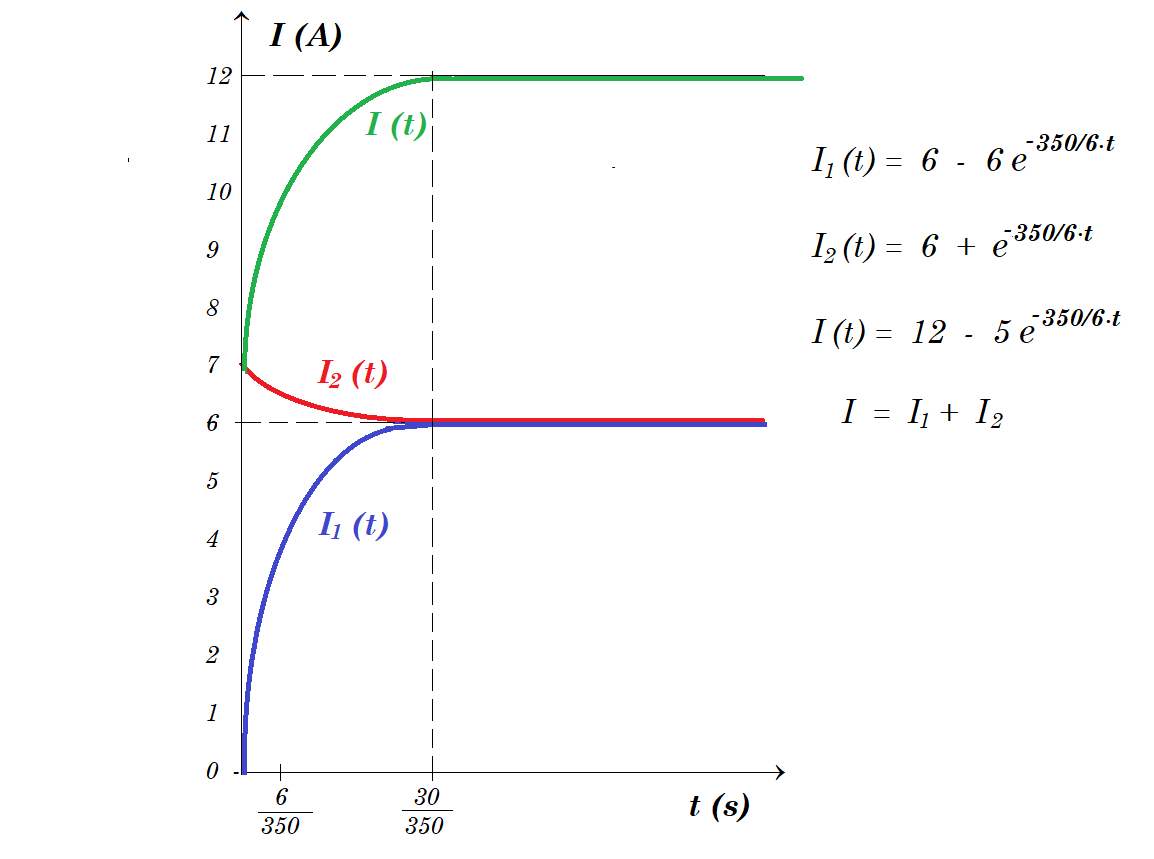
Για το κύκλωμα του σχήματος δίνονται R1=10Ω, R2= 10Ω, L=0,2Η, ενώ η πηγή έχει Ε=84V και εσωτερική αντίσταση r=2Ω και ο διακόπτης δ είναι ανοικτός. Σε μια στιγμή t=0 κλείνουμε τον διακόπτη δ.  Αμέσως μετά το κλείσιμο του διακόπτη:
Αμέσως μετά το κλείσιμο του διακόπτη:
- Ποια η ένταση του ρεύματος που διαρρέει κάθε κλάδο του κυκλώματος;
- Πόση είναι η πολική τάση της πηγής και ποια η τάση στα άκρα του πηνίου;
- Με ποιο ρυθμό αυξάνεται το ρεύμα που διαρρέει το πηνίο;
- Πόση ενέργεια τελικά αποθηκεύεται στο πηνίο;
μόλις κλείσει ο διακόπτης δ ο κλάδος με το πηνίο δεν διαρρέεται από ρεύμα έτσι έχουμε : Ε = Ι (R2 + r) => I = 84V/12Ω = 7 Α
Vπολική = E - I r = 84 - 7 2 = 70 V = VΑΓ = Vπηνίου
Vπηνίου = |Εαυτεπαγ| = L ΔΙ/Δt => ΔΙ/Δt = Vπηνίου / L = 70 V / 0,2 H = 140 A/s
οταν αποκατασταθούν τα ρεύματα Ε = Ι ( r + R1R2/(R1+R2) ) => I = 84 / ( 2 + 5 ) = 12 A
Vπολική = E - I r = 84 - 12 2 = 60 V = VΑΓ
οι αντιστάσεις διαρρέονται από ρεύματα : Ι1 = VΑΓ / R1 = 60 / 10 = 6 Α και Ι2 = VΑΓ / R2 = 60 / 10 = 6 Α
ενέργεια του μαγνητικού πεδίου του πηνίου : UL = 0,5 L I2 = 0,5 0,2 62 = 3,6 Joule
I = I1 + I2 (1)
Vπολική = E - Ι r = Ι2 R2 = VΑΓ = L dI1 /dt + I1 R1 => 84 - Ι 2 = I2 10 = 0,2 dI1 /dt + I1 10 =>
=> 42 - Ι = 5 I2 = 0,1 dI1 /dt + 5 I1 (2)
(2),(1) => 42 - I1 - I2 = 5 I2 = 0,1 dI1 /dt + 5 I1
οπότε 42 - I1 - I2 = 5 I2 => 42 - I1 = 6 I2 => 7 - I1 /6 = I2
και 5 I2 = 0,1 dI1/dt + 5 I1 => 5 (7 - I1/6) = 0,1 dI1/dt + 5 I1 =>
=> 35 - 5/6 I1 = 0,1 dI1/dt + 5 I1 => 0,1 dI1/dt = 35 - 5 I1 - 5/6 I1 =>
=> 0,1 dI1/dt = - 35/6 I1 + 35 => dI1/dt = - 350/6 ( I1 - 6 ) =>
=> dI1 / ( I1 - 6 ) = - 350/6 dt => ln ( ( I1 - 6 ) / ( - 6 ) ) = - 350/6 . t => I1(t) = 6 - 6 e-350/6 t
I2 = 7 - I1/6 = 7 - 1/6 ( 6 - 6 e-350/6 t ) = 7 - 1 + e-350/6 t => I2(t) = 6 + e-350/6 t
I = I1 + I2 => I(t) = 12 - 5 e-350/6 t
t = 0 I1(0) = 6 - 6 e0 = 6 - 6 = 0 I2(0) = 6 + e0 = 6 + 1 = 7 A I(0) = 7 A
t ® ¥ Ι1 = 6 Α Ι2 = 6 Α Ι = 12 Α
...................................................................................................................................................................................
Στο κύκλωμα του σχήματος βλέπετε μια ηλεκτρική πηγή χωρίς εσωτερική αντίσταση, που τροφοδοτεί δύο κλάδους παράλληλους. Ο ένας περιλαμβάνει ένα λαμπτήρα και ο άλλος ένα ιδανικό πηνίο και έναν αντιστάτη σε σειρά.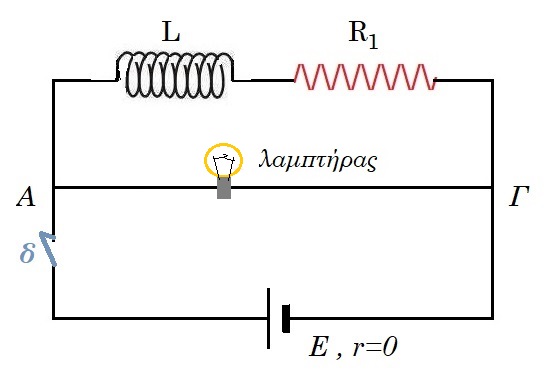
α) Μόλις κλείσουμε το διακόπτη:
i) Ο κλάδος ΑΓ διαρρέεται από ρεύμα με φορά από το Α --> Γ που η αρχική του τιμή είναι Ε/R1 .
ii) Ο λαμπτήρας διαρρέεται από ρεύμα σταθερής έντασης.
iii) Στο πηνίο αναπτύσσεται ΗΕΔ από αυτεπαγωγή με αρνητικό πόλο το άκρο Α.
iv) Η τελική διαφορά δυναμικού στα άκρα του αντιστάτη R1 είναι μικρότερη από Ε.
β) Αφήνουμε για αρκετό χρόνο κλειστό το διακόπτη και αφού σταθεροποιηθεί η ένταση του ρεύματος σε μια στιγμή, έστω t=0, ανοίγουμε το διακόπτη δ.
i) Ο λαμπτήρας θα σβήσει αμέσως.
ii) Το πηνίο διαρρέεται από σταθερό ρεύμα με φορά από το Α --> Γ.
iii) Η ενέργεια του μαγνητικού πεδίου του πηνίου μετατρέπεται εξολοκλήρου σε θερμότητα πάνω στον αντιστάτη R.
iv) Η αρχική ΗΕΔ από αυτεπαγωγή που αναπτύσσεται στο πηνίο είναι ίση με: Εαυτ= Ε·(R1+RΛ)/R1
Ποια πρόταση είναι σωστή σε κάθε υποερώτημα;
α (ii)
b (iv) τη στιγμή που ανοίγουμε τον διακόπτη ο πάνω κλάδος διαρρέεται από μέγιστο ρεύμα Ι0=Ε/R. το ρεύμα αυτό θα περάσει και από τον λαμπτήρα. Έτσι λόγω επαγωγής το κύκλωμα θα συνεχίσει να διαρρέεται από ρεύμα και αιτία θα είναι η ΗΕΔ από αυτεπαγωγή με τιμή: Εαυτ=Ι0·(R+RΛ)= Ε·(R+RΛ)/R.
...............................................................................................................................................................
Στο κύκλωμα του σχήματος η πηγή έχει ηλεκτρεγερτική δύναμη E = 24 V και αμελητέα εσωτερική αντίσταση. Ο αντιστάτης έχει αντίσταση R = 10 Ω. Το πηνίο είναι ιδανικό και έχει συντελεστή αυτεπαγωγής L = 0,02 Η. Αρχικά ο μεταγωγός μ βρίσκεται τη θέση Α και το κύκλωμα διαρρέεται με σταθερό ρεύμα Ι0. Να υπολογισθεί η τιμή Ι0.
Αρχικά ο μεταγωγός μ βρίσκεται τη θέση Α και το κύκλωμα διαρρέεται με σταθερό ρεύμα Ι0. Να υπολογισθεί η τιμή Ι0.
α) Ο μεταγωγός απότομα μεταφέρεται στη θέση Β. Κάποια στιγμή, το ρεύμα στο κύκλωμα έχει τιμή i = 1 Α. Να υπολογιστεί η ηλεκτρεγερτική δύναμη από αυτεπαγωγή στο πηνίο , ο ρυθμός μεταβολής του ρεύματος και ο ρυθμός μεταβολής της ενέργειας του μαγνητικού πεδίου του πηνίου την ίδια στιγμή.
β) Να υπολογισθεί η θερμότητα που παράγεται στο κύκλωμα, από τη στιγμή που ο μεταγωγός μεταφέρεται στη θέση Β μεχρι να μηδενιστεί το ρεύμα στο κύκλωμα.
γ) Μετά από αρκετό χρόνο μεταφέρεται απότομα ο μεταγωγός από τη θέση Β στη θέση Α.
γ1) Να υπολογισθεί η τελική τιμή του ρεύματος.
γ2) Κάποα στιγμή το ρεύμα έχει ένταση i = 2 Α. Να υπολογιστεί η ηλεκτρεγερτική δύναμη από αυτεπαγωγή στο πηνίο , ο ρυθμός μεταβολής του ρεύματος τη στιγμή αυτή και ο ρυθμός με τον οποίο αποθηκεύεται ενέργεια στο μαγνητικό πεδίο του πηνίου την ίδια στιγμή.
Ι0 = E / R = 24 V / 10 Ohm = 2,4 A
(α) όταν ο μεταγωγός μεταφερθεί στη θέση Β το πηνίο αντιδρά στη μεταβολή της μαγνητικής ροής ( μειώνεται ) που διέρχεται μέσα από τις σπείρες του με συνέπεια να αναπτυχθεί επαγωγική τάση στις άκρες του και το επαγωγικό ρεύμα έχει την ίδια φορά με το αρχικό ισχύει η σχέση : Εαυτεπαγ = i R => - L di/dt = i R => di/i = - R/L dt => ln ( i/I0) = - R/L t => i(t) = I0 e-R/L t η ένταση του ρεύματος μειώνεται εκθετικά με το χρόνο
i(t) = I0 e-R/L t => di/dt = - I0 R/L e-R/L t
όταν η ένταση i = 1 Α η πτώση τάσης στα άκρα της αντίστασης είναι VR = i R = 1 A 10 Ohm = 10 Volt τόση είναι και η τάση αυτεπαγωγής του πηνίου - L di/dt = i R => - 0,02 di/dt = 10 => di/dt = - 500 Α/s εκείνη τη στιγμή το ρεύμα μειώνεται κατά 500 αμπέρ κάθε δευτερόλεπτο
η ενέργεια του μαγνητικού πεδίου του πηνίου είναι : UL = 0,5 L i2 = 0,5 0,02 12 = 0,01 J
ο ρυθμός μεταβολής της είναι : dUL / dt = L i di/dt = 0,02 1 (-500) = - 10 J/s < 0
η ισχύς του ηλεκτρικού ρεύματος που καταναλώνεται στο κύκλωμα : PR = i2 R = 12 10 = 10 Watt = VR i
συμπέρασμα |dUL / dt| = PR = 10 Watt = |- 10 J/s|
ο ρυθμός που μειώνεται η ενέργεια του μαγνητικού πεδίου του πηνίου ισούται με την ισχύς του ηλεκτρικού ρεύματος που καταναλώνεται στο κύκλωμα ( πάνω στην R )
(β) όταν ο μεταγωγός ήταν στη θέση Β το πηνίο είχε δυναμική ενέργεια μαγνητικού πεδίου UL = 0,5 L I02 = 0,5 0,02 2,42 = 0,0576 Joule η ενέργεια αυτή μετατρέπεται σε θερμότητα πάνω στην αντίσταση
(γ) όταν ο μεταγωγός μεταφερθεί από θέση Β στη θέση Α το πηνίο αντιδρά λόγω της μεταβολής της μαγνητικής ροής ισχύει η σχέση : Ε + Εαυτεπαγ = i R => Ε - L di/dt = i R => Ε - i R = L di/dt => L di/dt = - R(i - Ε/R) => di / (i - Ε/R) = - R/L dt => ln [ (i - Ε/R) / (- Ε/R) ] = - R/L t => (i - Ε/R) / (- Ε/R) = e - R/L t => => (i - Ε/R) = (- Ε/R) e - R/L t => i(t) = Ε/R ( 1 - e - R/L t ) η ένταση του ρεύματος αυξάνεται εκθετικά με το χρόνο (γ1) η τελική τιμή του ρεύματος είναι : Ι = E / R = 24 V / 10 Ohm = 2,4 A
i(t) = Ε/R ( 1 - e - R/L t ) => di/dt = + E/L e - R/L t
(γ2) όταν i = 2 Α τότε έχουμε τη σχέση : Ε + Εαυτεπαγ = i R => 24 + Εαυτεπαγ = 2 10 => Εαυτεπαγ = - 4 V - L di/dt = - 4 V => - 0,02 di/dt = - 4 => di/dt = + 200 Α/s εκείνη τη στιγμή το ρεύμα αυξάνεται κατά 200 αμπέρ κάθε δευτερόλεπτο
η ενέργεια του μαγνητικού πεδίου του πηνίου είναι : UL = 0,5 L i2 = 0,5 0,02 22 = 0,04 J
ο ρυθμός μεταβολής της είναι : dUL / dt = L i di/dt = 0,02 2 (+200) = + 8 J/s
η ισχύς του ηλεκτρικού ρεύματος που καταναλώνεται στο κύκλωμα : PR = i2 R = 22 10 = 40 Watt
η ισχύς που παρέχει η πηγή στο κύκλωμα : Pπηγής = E i = 24 V 2 A = 48 Watt
συμπέρασμα |dUL / dt| + PR = + 8 J/s + 40 W = 48 Watt = Pπηγής
ο ρυθμός που αποθηκεύεται ενέργεια στο μαγνητικό πεδίο του πηνίου συν την ισχύ του ηλεκτρικού ρεύματος που καταναλώνεται στο κύκλωμα ( πάνω στην R ) ισούται με την ισχύ που παρέχει η πηγή στο κύκλωμα
.................................................................................................................................................
Στο κύκλωμα του σχήματος η πηγή έχει ηλεκτρεγερτική δύναμη E = 10 V και εσωτερική αντίσταση r = 1 Ω, το πηνίο είναι ιδανικό με συντελεστή αυτεπαγωγής L = 0,2 H φέρει σιδηροπυρήνα με μαγνητική διαπερατότητα μ = 105 /8π και Ν/l = 100 σπείρες / μέτρο μήκους, ο αντιστάτης έχει ωμική αντίσταση R = 3 Ω. Ο άξονας του πηνίου είναι κάθετος στο επίπεδο του κυκλικού αγωγού εμβαδού = 10 cm2 που βρίσκεται κοντά στο άκρο του πηνίου. Σε μια στιγμή t=0 κλείνουμε τον διακόπτη. Την στιγμή t1 ο αντιστάτης διαρρέεται από ρεύμα i1 = 0,5 A . Για τη στιγμή αυτή να βρεθούν :
α) η ΗΕΔ από αυτεπαγωγή που αναπτύσσεται στο πηνίο
β) ο ρυθμός μεταβολής της έντασης του ρεύματος που διαρρέει το κύκλωμα
γ) η ενέργεια του μαγνητικού πεδίου του πηνίου καθώς και ο ρυθμός μεταβολής της.
δ) αν ο κυκλικός αγωγός έχει ωμική αντίσταση r2 = 0,1 Ω να βρεθεί η ένταση i2 του ρεύματος που τον διαρρέει και το φορτίο που διέρχεται από μια διατομή του κυκλικού αγωγού
ε) με ποιο ρυθμό μεταφέρεται ενέργεια από το πηνίο στον κυκλικό αγωγό μέσω του μαγνητικού πεδίου;
Το μαγνητικό πεδίο του κυκλικού αγωγού έχει αμελητέα επίδραση στο πηνίο.
νόμος του Οhm : Ε + Εαυτεπαγ = i1 ( R + r ) => 10V + Εαυτεπαγ = 0,5A ( 3Ω + 1Ω ) => Εαυτεπαγ = - 10V + 2V = - 8V
Εαυτεπαγ = - L di/dt => di/dt = - Εαυτεπαγ / L = - (- 8V) / 0,2H = + 40 A/s
Δi1 / Δt = 0,5/Δt = 40 A/s => Δt = 1/80 s
UL = 0,5 L i12 = 0,5 0,2 0,52 = 0,025 J dUL / dt = L i1 di/dt = 0,2 0,5 (+40) = + 4 J/s
B1 = μ 4π 10-7 i1 N/l = 105/ 8π 4π 10-7 0,5 100 = 0,25 Tesla στο άκρο του πηνίου : Β = 0,125 Τ
Φ1 = Β Α = 0,125 Τ 10-3 m2 = 125 10-6 Wb
Eεπαγ = - dΦ/dt = - A dB/dt = - A ½ 4π 10-7 N/l di1/dt = - 10-3 ½ 4π 10-7 107/8π 40 = - 0,01 Volt
i2 = Eεπαγ / r2 = - 0,01V / 0,1Ω = - 0,1 A
το πηνίο διαρρέεται από ρεύμα και εμφανίζεται μαγνητικό πεδίο οριζόντιο προς τα δεξιά ο βόρειος πόλος η μαγνητική ροή που διέρχεται μέσα από τον κυκλικό αγωγό αυξάνεται οπότε ο αγωγός αντιδρά και προσπαθεί να διώξει το μαγνητικό πεδίο του πηνίου έτσι διαρρέεται από ρεύμα i2 που δημιουργεί μαγνητικό πεδίο οριζόντιο προς τα αριστερά ο βόρειος πόλος
q = ΔΦ / r2 = Α Β / r2 = 10-3 m2 0,125 T / 0,1 Ω = 125 10-5 C
η πηγή παρέχει ισχύ : Ε i1 = 10V 0,5A = 5 Watt
στις ααντιστάσεις καταναλώνεται ισχύς : i12 ( R + r ) = 0,52 4 = 1 Watt άρα 5 W - 1 W = 4 J/s = dUL/dt
...................................................................................................................................
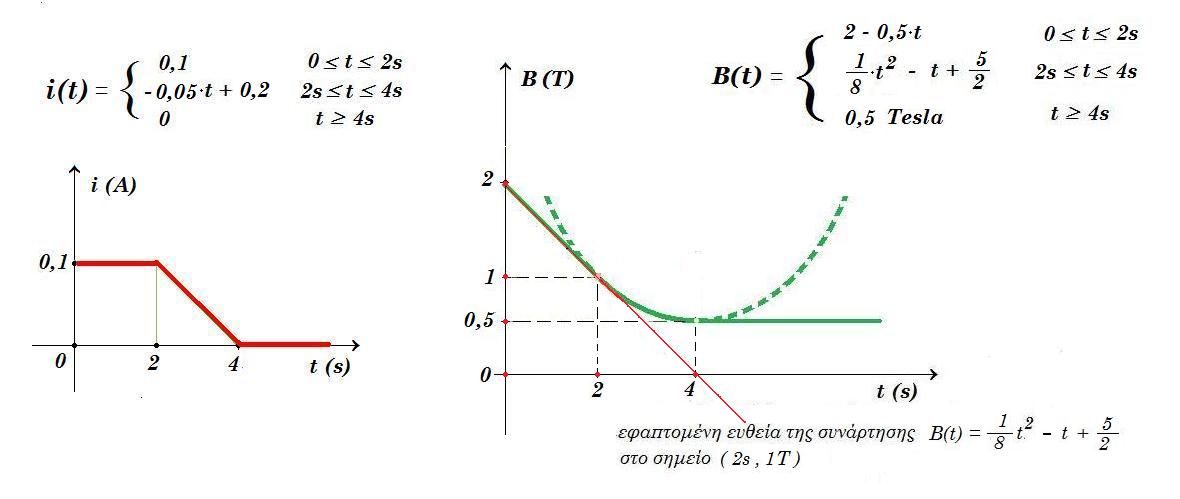
Στο σχήμα, το σωληνοειδές που έχει Ν = 100 σπείρες με εμβαδόν Α = 0,01 m2 η κάθε μία, βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο (εξωτερικό) εντάσεως Β0 = 2 Τ, με τον άξονά του παράλληλο στις δυναμικές γραμμές. Το πηνίο έχει ωμική αντίσταση r = 2 Ω ενώ τα άκρα του συνδέονται με αντιστάτη που έχει ωμική αντίσταση R = 3 Ω, παράλληλα στον οποίο συνδέεται ιδανικό βολτόμετρο.
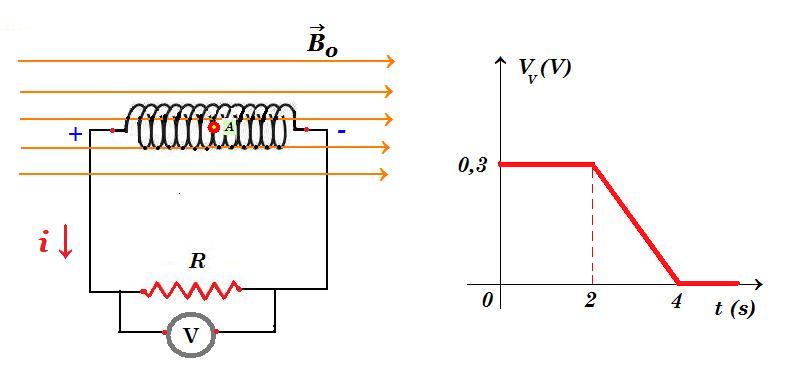
Κάποια στιγμή t = 0 αρχίζουμε να μεταβάλλουμε το μέτρο της έντασης του εξωτερικού μαγνητικού πεδίου, με αποτέλεσμα ο αντιστάτης να διαρρέεται από ρεύμα με φορά όπως στο σχήμα, ενώ η ένδειξη του βολτομέτρου μεταβάλλεται όπως στο διάγραμμα.
Α) Εξηγήστε γιατί δημιουργείται τάση στα άκρα του αντιστάτη.
Β) Πως μεταβάλλεται η ένταση του εξωτερικού μαγνητικού πεδίου από t=0 έως t=4s; Αυξάνεται ή μειώνεται η ένταση;
Γ) Τη στιγμή t = 2s η ένταση του εξωτερικού μαγνητικού πεδίου είναι Β1, τότε στο σημείο Α, το μέσον του πηνίου, το συνολικό μαγνητικό πεδίο ΒΑ είναι :
α) ΒΑ < Β1 β) ΒΑ = Β1 γ) ΒΑ > Β1
Α) μεταβάλλοντας την ένταση του εξωτερικού μαγνητικού πεδίου μεταβάλλεται η μαγνητική ροή των δυναμικών γραμμών που διέρχονται μέσα από τις σπείρες του πηνίου, οπότε το πηνίο αντιδρά και γίνεται "ηλεκτρική πηγή" αναπτύσσεται επαγωγική τάση Εεπαγ οπότε διαρρέεται από ρεύμα τέτοιο ώστε να δημιουργηθεί μαγνητικό πεδίο με σκοπό να αναιρέσει την μεταβολή της μαγνητικής ροής
Β) η φορά του ρεύματος μας που διαρρέει το πηνίο δείχνει ότι στο πηνίο επάγεται μαγνητικό πεδίο ομόρροπο του εξωτερικού μαγνητικού πεδίου που σημαίνει ότι το εξωτερικό μαγνητικό πεδίο μειώνεται ( dB/dt < 0 )
0 £ t £ 2s i = VV / R = 0,3 V / 3 Ω => i = 0,1 A
Εεπαγ = i (r + R) = 0,1 ( 2 + 3 ) = 0,5 V => Εεπαγ = 0,5 Volt επαγωγική τάση πηνίου
Εεπαγ = - Ν ΔΦ/Δt = - N Α ΔΒ/Δt => ΔB/Δt = - Εεπαγ / Ν.A = - 0,5 / 1 = - 0,5 T/s => ΔΒ/Δt = - 0,5 T/s
dB/dt = -0,5 => dB = -0,5 dt => B(t) - B(0) = -0,5 (t - 0) => B(t) = B(0) - 0,5 t = 2 - 0,5 t 0 £ t £ 2s
B(0) = 2 Tesla (δεξιά) B(2) = 2 - 0,5 2 = 1 Tesla (δεξιά)
2s £ t £ 4s VV(t) = - 0,15 t + 0,6 => i = VV / R = (- 0,15 t + 0,6) / 3 => i(t) = - 0,05 t + 0,2
Εεπαγ(t) = i(t) (r + R) => Εεπαγ(t) = (- 0,05 t + 0,2) ( 2 + 3 ) = - 0,25 t + 1
Εεπαγ = - Ν ΔΦ/Δt = - N Α ΔΒ/Δt => ΔB/Δt = - Εεπαγ / Ν.A = - (- 0,25 t + 1) / 1 = 0,25 t - 1
=> ΔΒ/Δt = 0,25 t - 1 2s £ t £ 4s
dB/dt = 0,25 t - 1 => dB = (1/4 t - 1) dt => B(t) - B(2) = 1/8 (t2 - 22) - 1 (t - 2) =>
=> B(t) - 1 = 1/8 t2 - 1/2 - t + 2 => B(t) = 1/8 t2 - t + 5/2 2s £ t £ 4s
B(2) = 1/8 22 - 2 + 2,5 = 0,5 - 2 + 2,5 = 1 Τ
B(4) = 1/8 42 - 4 + 2,5 = 2 - 4 + 2,5 = 0,5 Τ
Γ) η φορά του ρεύματος μας που διαρρέει το πηνίο δείχνει ότι στο πηνίο επάγεται μαγνητικό πεδίο ομόρροπο του εξωτερικού μαγνητικού πεδίου του οποίου η ένταση μειώνεται
το πηνίο αντιδρά στη μεταβολή του εξωτερικού μαγνητικού πεδίου έτσι ώστε να διατηρήσει αμετάβλητη την αρχική μαγνητική ροή που διέρχεται μέσα από τις σπείρες του, η οποία είναι : Φαρχική = 2 Τ 0,01 m2 = 0,02 Wb για αυτό το λόγο εμφανίζεται επαγωγική τάση και διαρρέεται από ρεύμα το οποίο δημιουργεί μαγνητικό πεδίο Βπην η συνολική ένταση του μαγνητικού πεδίου στο μέσον Α του πηνίου είναι ΒΑ = Βεξ + Βπην
η συνολική ένταση του μαγνητικού πεδίου στο μέσον Α του πηνίου πρέπει να είναι ΒΑ = 2 Τ
τη στιγμή t = 2s η τιμή του εξωτερικού μαγνητικού πεδίου είναι Β1 = 1Τ οπότε ΒΑ > Β1