Στο σχήμα απεικονίζονται ένας ευθύγραμμος αγωγός πολύ μεγάλου μήκους που διαρρέεται από σταθερό ρεύμα έντασης  I₁ = 20 A  και σε απόσταση  d = 0,1 m  ένα τετραγωνικό πλαίσιο ΚΛΜΝ, ομοεπίπεδο με τον ευθύγραμμο αγωγό.  Ο αγωγός και το πλαίσιο βρίσκονται πάνω σε λείο οριζόντιο επίπεδο.  Το πλαίσιο έχει πλευρά μήκους   l = 0,1 m  μάζα m = 0,1 kg   και διαρρέεται με ρεύμα έντασης  I₂ = 10 A  με φορά ίδια με αυτήν των δεικτών του ρολογιού.  Στην περιοχή που ορίζουν οι ευθείες Ay και A΄y΄ υπάρχει κατακόρυφο ομογενές μαγνητικό πεδίο έντασης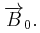  
Το πλαίσιο ισορροπεί λόγω των δυνάμεων που δέχεται από τον ευθύγραμμο αγωγό και το μαγνητικό πεδίο 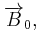ενώ ο ευθύγραμμος κρατιέται ακίνητος από εμάς.
Α1)  Να υπολογίστε τις δυνάμεις που δέχονται οι πλευρές ΚΛ και ΜΝ από τον ευθύγραμμο αγωγό, καθώς και τη δύναμη που δέχεται ο ευθύγραμμος αγωγός από το πλαίσιο.
Α2)  Να προσδιορίσετε την κατεύθυνση των δυναμικών γραμμών του μαγνητικού πεδίου 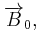καθώς και το μέτρο της έντασής του.
Διπλασιάζουμε την ένταση του ρεύματος που διαρρέει τον ευθύγραμμο αγωγό.
Β1)  Να προσδιορίσετε προς ποια κατεύθυνση θα κινηθεί το πλαίσιο και το μέτρο της αρχικής του επιτάχυνσης.
Β2)  Να υπολογίσετε τη δύναμη που δέχεται το πλαίσιο, τη στιγμή που εξέρχεται του μαγνητικού πεδίου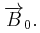

Α)       F_L,ΚΛ  =  10^-7  2 Ι₁ Ι₂ l / d  =  10^-7  2  20  10  0,1 / 0,1   =  4 10^-5 N        ¬

           F_L,ΜΝ  =  10^-7  2 Ι₁ Ι₂ l / (d+l)  =  10^-7  2  20  10  0,1 / 0,2   =  2 10^-5 N     ®  

           F_L,ΜΝ,2  =  Β₀  Ι₂  l     ®   για να ισορροπεί το πλαίσιο 

ΣF_{πλαισίου}  =   F_L,ΜΝ  +  F_L,ΜΝ,2  -  F_L,ΚΛ  =>  0  =  2 10^-5  +  F_L,ΜΝ,2  -  4 10^-5  =>    F_L,ΜΝ,2  =  2 10^-5 Ν  =>  

                     =>    Β₀  Ι₂  l  =  2 10^-5 Ν  =>   Β₀  10  0,1  =  2 10^-5 Ν  =>  Β₀=  2 10^-5 Τ    Δ          

Β)       F_L,ΚΛ  =   10^-7  2 Ι₁ Ι₂ l / d  =   10^-7  2  40  10  0,1 / 0,1   =  8 10^-5 N        ¬

           F_L,ΜΝ  =   10^-7  2 Ι₁ Ι₂ l / (d+l)  =   10^-7  2  40  10  0,1 / 0,2   =  4 10^-5 N     ®  

           F_L,ΜΝ,2  =  Β₀  Ι₂  l  = 2 10^-5  10  0,1  = 2 10^-5 Ν   ®    

ΣF_{πλαισίου}  =   F_L,ΜΝ  +  F_L,ΜΝ,2  -  F_L,ΚΛ  =  4 10^-5  +  2 10^-5  -  8 10^-5  =>   ΣF_{πλαισίου}  =  - 2 10^-5 Ν   ¬   

το πλαίσιο θα κινηθεί προς τα αριστερά με αρχική επιτάχυνση   α = ΣF_{πλαισίου} / m  = 2 10^-5 / 0,1  = 2 10^-4 m/s²         

           F_L,ΚΛ  =   10^-7  2 Ι₁ Ι₂ l / (d/2)  =   10^-7  2  40  10  0,1 / 0,05   =  16 10^-5 N        ¬

           F_L,ΜΝ  =   10^-7  2 Ι₁ Ι₂ l / (3d/2)  =   10^-7  2  40  10  0,1 / 0,15   =  16/3 10^-5 N     ®  

ΣF_{πλαισίου}  =   F_L,ΜΝ  -  F_L,ΚΛ  =  16/3 10^-5   -  16 10^-5  =>   ΣF_{πλαισίου}  =  - 32/3 10^-5 Ν   ¬                          

....................................................................................................................................................................................................................................

Ένα πηνίο έχει Ν = 500 σπείρες, αντίσταση R₁= 1Ω και κάθε σπείρα του έχει εμβαδόν S =20cm². Το πηνίο βρίσκεται με τον άξονά του παράλληλο σε ομογενές μαγνητικό πεδίο έντασης Β=0,1 Τ. Συνδέουμε τις άκρες του πηνίου με αμπερόμετρο αντίστασης R₂= 1Ω και σε χρονικό διάστημα Δt=0,05s διπλασιάζουμε την ένταση του μαγνητικού πεδίου με σταθερό ρυθμό. Να υπολογίσετε: 

α)  την μαγνητική ροή που διέρχεται αρχικά από μία σπείρα του πηνίου.
β)  την ΗΕΔ από επαγωγή που αναπτύσσεται στα άκρα του πηνίου.
γ)  την ένδειξη του αμπερομέτρου.
δ)  το φορτίο που θα περάσει μέσα από το αμπερόμετρο.
ε)  την ηλεκτρική ισχύ στη αντίσταση R₁ του πηνίου.

  Φ_αρχική  =  Β S  =  0,1 T  20 10^-4 m²   = 2 10^-4  Wb

  Φ_τελική  =  2Β S  =  0,2 T  20 10^-4 m²   = 4 10^-4  Wb    

  ΔΦ = Φ_τελική  - Φ_αρχική  = 2 10^-4  Wb      

  Ε_επαγ  =  - N ΔΦ / Δt  =  - 500 2 10^-4  Wb  /  0,05 s  =  - 2 Volt 

  i  = Ε_επαγ  / (R₁ + R₂)  =  - 2V / 2 Ohm  =  - 1 A   

  q  =  i t  =  1 A  0,05 s  =  0,05 Coulomb  

  P_R1  =  i² R₁  =  1²  1  =  1 Watt  

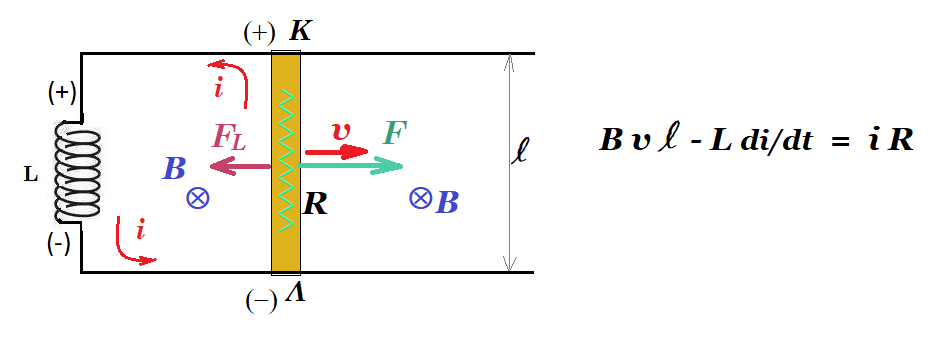
Δύο παράλληλοι οριζόντιοι αγωγοί Ax και A'x', χωρίς αντίσταση, που απέχουν μεταξύ τους  l = 0,5 m, συνδέονται στα άκρα τους με ιδανικό πηνίο συντελεστή αυτεπαγωγής  L = 0,025 H.   Ένας αγωγός ΚΛ, με μάζα  m = 150 g  και αντίσταση  R = 0,05 Ω, μπορεί να ολισθαίνει χωρίς τριβές μένοντας κάθετος και σε επαφή με τους παράλληλους αγωγούς. Το σύστημα βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο B = 0,1 T.  Ασκώντας στον αγωγό ΚΛ κάποια δύναμη F,  παράλληλη με τους οριζόντιους αγωγούς, τον κινούμε με τρόπο ώστε η ένταση του ρεύματος στο κύκλωμα να δίνεται από τη σχέση  i  =  2t + 3 (SI).

α)   Να υπολογιστεί η ηλεκτρεγερτική δύναμη από αυτεπαγωγή που δημιουργείται στο πηνίο κατά τη διάρκεια του φαινομένου.
β)   Να βρεθεί και να αποδοθεί γραφικά η σχέση που συνδέει την ταχύτητα του αγωγού ΚΛ με το χρόνο.
γ)   Να υπολογιστεί ο ρυθμός Δυ/Δt με τον οποίο αυξάνεται η ταχύτητα του αγωγού κατά τη διάρκεια του φαινομένου.
δ)   Να υπολογιστεί ο ρυθμός με τον οποίο προσφέρεται ενέργεια στο κύκλωμα μέσω του έργου της F, τη χρονική στιγμή t = 4s.

  i = 2t + 3     di/dt = 2 A/s          Ε_{αυτεπαγ}  =  - L di/dt  =  -  0,025  2  =  - 0,05 Volt   

  Ε_επαγ  =  B l v             Ε_επαγ + Ε_{αυτεπαγ}  =  i R  =>   B l v  +  (- L di/dt)  =  i R  =>   0,1  0,5  v  -  0,05  =  ( 2t + 3 ) 0,05    =>       v  -  1  =  2t + 3  =>  v  =  2t + 4  

  dv/dt  =  2 m/s²  =  a    

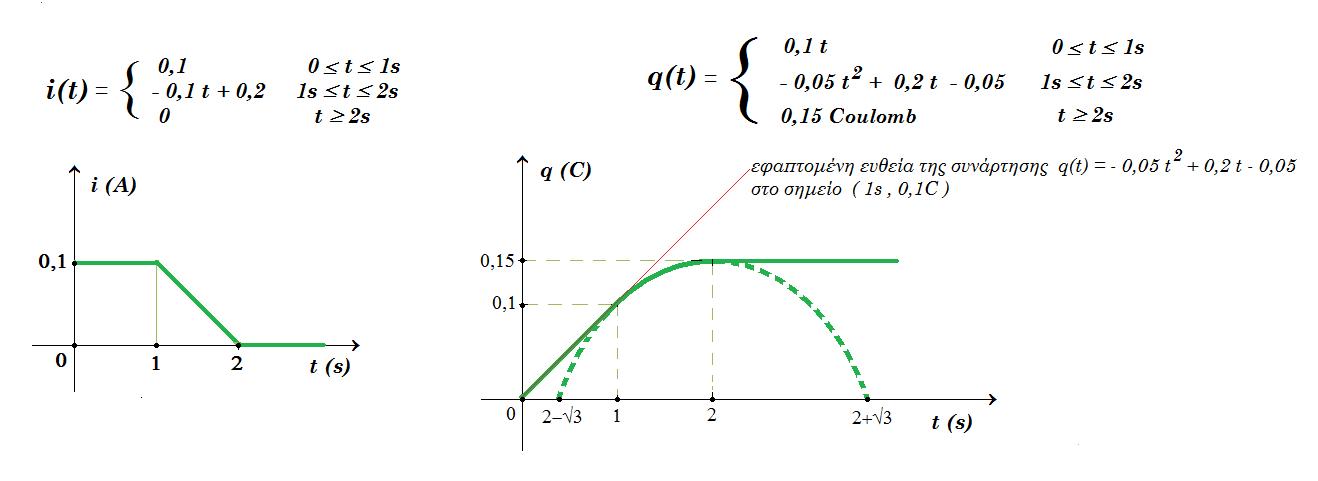
 F_L (t) =  B l i  =  0,1  0,5  (2t + 3)  =  0,1 t  +  0,15  

 P_FL(t)  =  F_L(t)  v(t)  =  ( 0,1t + 0,15)  ( 2t + 4 )  =>   P_FL(t)  =  0,2 t²  +  0,7 t  +  0,6    (1)

      ΣF  =  m a   =>   F  -  F_L  =  m a  =>   F  -  ( 0,1 t  +  0,15 )  =  0,15  2  =>   F  =   0,1 t  +  0,45 

      P_F (t)  =  F(t)  v(t)  =  ( 0,1 t  +  0,45 )  ( 2t + 4 )  =>   P_F (t)  =  0,2 t²  +  1,3 t  +  1,8    (2)

      P_F (4)  =  0,2 4²  +  1,3  4  +  1,8  =   3,2  +  5,2  +  1,8  =  10,2 J/s   

  K  =  0,5 m v²             dK/dt  =  m  v  dv/dt  =  0,15  ( 2t + 4 )  2  =>  dK/dt  =  0,6 t  +  1,2    (3)  

    (1) , (2) , (3)  =>   P_F (t)  = P_FL(t)  +  dK/dt

  P_R(t)  =  i²  R  =  ( 2t + 3)²  0,05  =>   P_R(t)  =  0,2 t²  +  0,6 t  +  0,45      (4)

  U_L  =  0,5  i²  L         dU_L/dt  =  L  i  di/dt  =  0,025  (2t + 3)  2  =  0,1t  0,15   (5)

    (1) , (4) , (5)  =>   P_FL(t)  = P_R(t)  + dU_L/dt      

.....................................................................................................................................................

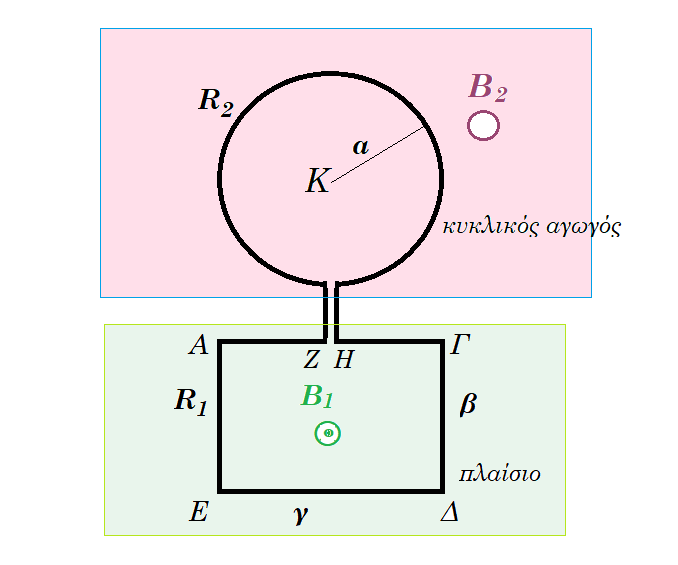
Το πλαίσιο ΑΓΔΕ του σχήματος έχει μορφή ορθογωνίου παραλληλογράμμου με διαστάσεις β=40cm και γ=50cm και ωμική αντίσταση R1= 0,12Ω.
Το επίπεδό του είναι κάθετο στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου έντασης Β₁ με φορά από τη σελίδα προς τον αναγνώστη.
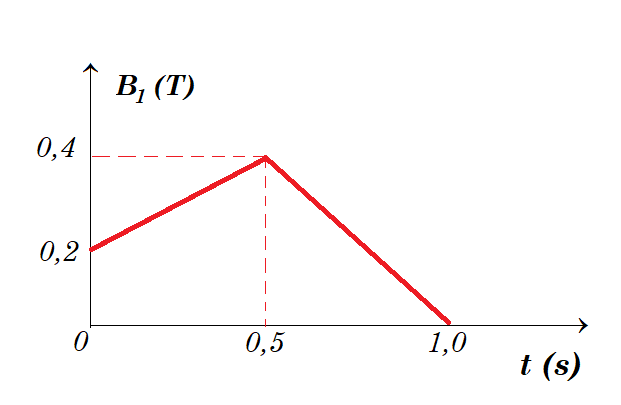
Τα άκρα ΖΗ του πλαισίου συνδέονται μέσω αγωγών αμελητέας αντίστασης με κυκλικό αγωγό ακτίνας α=20cm και ωμικής αντίστασης R2=0,04Ω και του οποίου το επίπεδο είναι κάθετο σε ένα δεύτερο ομογενές μαγνητικό πεδίο, Β₂ , σταθερού μέτρου και με φορά η οποία δεν είναι γνωστή.  Από τη χρονική στιγμή t=0s το μέτρο του μαγνητικού πεδίου Β₁ αρχίζει να μεταβάλλεται όπως δείχνεται στο διάγραμμα.  Για το χρονικό διάστημα από 0 έως 0,5s η συνολική ένταση του μαγνητικού πεδίου στο κέντρο Κ του κυκλικού αγωγού είναι μηδέν.
Γ1.  Να προσδιορίσετε τη φορά της έντασης του σταθερού μαγνητικού πεδίου Β₂.
Γ2.  Να σχεδιάσετε τη γραφική παράσταση της έντασης του επαγωγικού ρεύματος σε συνάρτηση με το χρόνο για το χρονικό διάστημα 0 έως 1 s.  
Γ3.  Να υπολογίσετε το μέτρο της συνολικής έντασης του μαγνητικού πεδίου στο κέντρο Κ του κυκλικού αγωγού για το χρονικό διάστημα από 0,5s έως 1 s.
Γ4.  Να υπολογίσετε τη χρονική στιγμή που στη διάταξη είχε αναπτυχθεί ποσό θερμότητας ίσο με Q/2, όπου με Q συμβολίζουμε το ποσό της θερμότητας που αναπτύχθηκε στη διάταξη μέχρι τη χρονική στιγμή 1,0 s.
Γ5.  Πόσο φορτίο περνά από μια διατομή του σύρματος του πλαισίου  από  0  έως  0,5s  και  από  0,5s  έως  1s;

Να αγνοήσετε φαινόμενα αμοιβαίας επαγωγής μεταξύ του πλαισίου και του κυκλικού αγωγού.   Δίνεται η μαγνητική σταθερά k_μ=10^-7Ν/Α²  

Γ1.  από  0  έως  0,5s  η ένταση του μαγνητικό πεδίο Β₁  αυξάνεται γραμμικά  από  0,2 Τ  έως  0,4 Τ  οπότε η μαγνητική ροή που διέρχεται από το πλαίσιο  ΑΓΔΕ  να αυξάνεται   ΔΦ  =  ΔΒ Α =  ΔΒ  β γ  =  (0,4Τ - 0,2Τ)  0,4m 0,5m  =  0,04 Wb    με συνέπεια  να αναπτυχθεί  επαγωγική τάση  στα άκρα του πλαισίου ΑΓΔΕ    Ε_επαγ  =  - ΔΦ/Δt  =  - 0,04 Wb / 0,5 s  =  - 0,08 Volt   έτσι το πλαίσιο διαρρέεται από ρεύμα  i_επαγ  =  E_επαγ / (R₁ + R₂)  =  - 0,08 / 0,16 =  - 0,5 A          

η ένταση του μαγνητικό πεδίο Β₁  αυξάνεται  οπότε  το επαγωγικό ρεύμα έχει τέτοια φορά  ώστε  να  μειώσει  την μαγνητική ροή  η οποία αυξάνεται   συνεπώς θα έχει δεξιόστροφη φορά  ώστε το μαγνητικό πεδίο που δημιουργεί να είναι αντίρροπο του  Β₁    

έτσι ο κυκλικός αγωγός διαρρέεται από το επαγωγικό ρεύμα  και   δημιουργείται μαγνητικό πεδίο  του οποίου η ένταση   στο κέντρο του  είναι   Β_κ  κάθετη στο επίπεδο  με φορά προς τα μέσα   Β_κ  =  10^-7 2π i_επαγ / α  =  10^-7 2π  0,5 / 0,2  =  5π 10^-7 Τ         επειδή η συνολική ένταση του μαγνητικού πεδίου στο κέντρο Κ  του κυκλικού αγωγού είναι  μηδέν  συμπεραίνουμε ότι  το μαγνητικό πεδίο Β₂  είναι  αντίθετο του  Β_κ  =  5π 10^-7 Τ   ( κάθετο στο επίπεδο  με φορά προς τα έξω ) 

Γ2.  από  0,5s  έως  1s  η ένταση του μαγνητικό πεδίο Β₁  μειώνεται γραμμικά  από  0,4 Τ  έως  0 Τ  οπότε η μαγνητική ροή που διέρχεται από το πλαίσιο  ΑΓΔΕ  να μειώνεται   ΔΦ  =  ΔΒ Α =  ΔΒ  β γ  =  (0 Τ - 0,4 Τ)  0,4m 0,5m  = - 0,08 Wb    με συνέπεια  να αναπτυχθεί  επαγωγική τάση  στα άκρα του πλαισίου ΑΓΔΕ    Ε_επαγ  =  - ΔΦ/Δt  =  - (- 0,08 Wb) / 0,5 s  =  + 0,16 Volt   έτσι το πλαίσιο διαρρέεται από ρεύμα  i_επαγ  =  E_επαγ / (R₁ + R₂)  =  + 0,16 / 0,16 =  + 1 A            

η ένταση του μαγνητικό πεδίο Β₁  μειώνεται  οπότε  το επαγωγικό ρεύμα έχει τέτοια φορά  ώστε να  αυξήσει  την μαγνητική ροή  η οποία  μειώνεται    συνεπώς θα έχει αριστερόστροφη φορά  ώστε το μαγνητικό πεδίο που δημιουργεί να είναι  ομόρροπο του  Β₁  

Γ3.    έτσι ο κυκλικός αγωγός διαρρέεται από το επαγωγικό ρεύμα  και   δημιουργείται μαγνητικό πεδίο  του οποίου η ένταση   στο κέντρο του  είναι   Β_κ  κάθετη στο επίπεδο  με φορά προς τα  έξω   Β_κ  =  10^-7 2π i_επαγ / α  =  10^-7 2π  1 / 0,2  =  π 10^-6 Τ            τα  Β_κ  και  Β₂  είναι τώρα ομόρροπα  με φορά προς τα έξω    Β_ΟΛΙΚΌ  =  Β_κ  +  Β₁  =  π 10^-6 Τ  +  5π 10^-7 Τ  =  1,5π 10^-6 Τ  =  1,5π μΤ    για το χρονικό διάστημα από  0,5s  έως 1s

Γ4.    η θερμότητα που αναπτύσσεται στο κύκλωμα   από  0  έως 1 s   είναι :   Q  =  i² R  t  =   0,5²   0,16  0,5  +   1²  0,16  0,5  =   0,02  +  0,08  =  0,1 Joule  

  Q / 2  =  0,05 J    =   1²  0,16  t  =>   t  =  0,05 / 0,16  =  0,3125 sec                  1 s  -  0,3125 s  =  0,6875 s

     0,5²  0,16  0,5  +   1²  0,16  (0,6875 - 0,5)  =    0,02 J  +  0,03 J  =  0,05 J

 Γ5.    ΔΦ / (R₁ + R₂)   =  0,04 Wb / 0,16 Ω  =  0,25 Coulomb  =  0,5 A  0,5 sec  =  i_επαγ  Δt     

          ΔΦ / (R₁ + R₂)   =  0,08 Wb / 0,16 Ω  =  0,5 Coulomb  =  1 A  0,5 sec  =  i_επαγ  Δt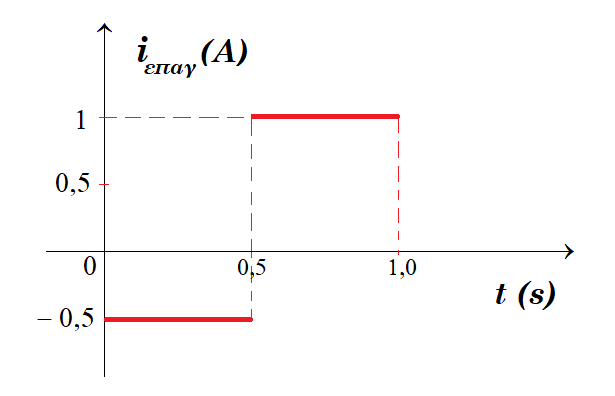  

Ο ευθύγραμμος απείρου μήκους αγωγός  ε, διαρρέεται από ρεύμα εντάσεως Ι  ενώ σε ένα σημείο του διακόπτεται  σχηματίζοντας κυκλικό αγωγός ακτίνας ρ   και κέντρου Ο.    Α) Η ένταση του μαγνητικού πεδίου στο κέντρο Ο του κυκλικού αγωγού είναι:    α)   παράλληλη στον αγωγό ε    β)   κάθετη στο επίπεδο του σχήματος με φορά προς τα έξω    γ)   κάθετη στο επίπεδο του σχήματος με φορά προς τα μέσα.  Β) Το μέτρο της έντασης Β του μαγνητικού πεδίου στο κέντρο Ο έχει μέτρο:    α)   Β < 10-7 4Ι / ρ         β)   Β = 10-7 4Ι / ρ          γ)   Β > 10-7 4Ι / ρ

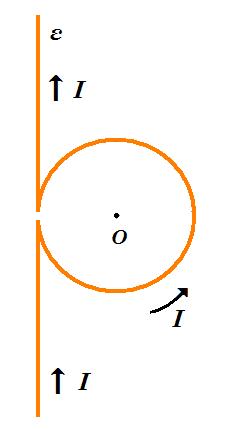   Β_ε = 10^-7 2Ι/ρ   κάθετα στο επίπεδο προς τα μέσα           Β_κ = 10^-7 2πΙ/ρ   κάθετα στο επίπεδο προς τα έξω

  Β_ολικό =  Β_κ - Β_ε  =  10^-7 2πΙ/ρ  - 10^-7 2Ι/ρ =  10^-7 2Ι(π-1)/ρ  > 10^-7 4Ι/ρ   κάθετα στο επίπεδο προς τα έξω

.......................................................................................................................................................................

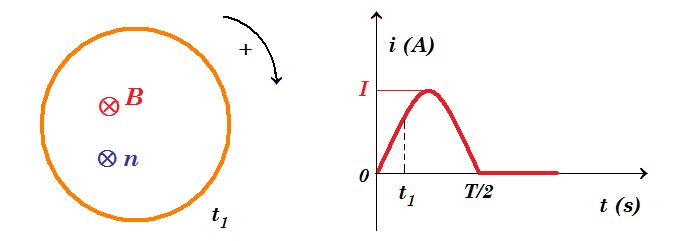Κυκλικός αγωγός ακτινας  ρ  και  ωμικής αντίστασης R  βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο  κάθετα στις δυναμικές γραμμές του.  Κάποια στιγμή έχουμε μεταβολή της έντασης του πεδίου με αποτέλεσμα ο αγωγός να διαρρέεται από επαγωγικό ρεύμα  η ένταση του οποίου μεταβάλλεται όπως στο διάγραμμα  ( i = I ημωt ). 

Τη στιγμή t₁  η ένταση του μαγνητικού πεδίου αυξάνεται  ή   μειώνεται ;

Εκφράστε την μαγνητική ροή Φ που διέρχεται από το επίπεδο το κυκλικού  αγωγού συναρτήσει του χρόνου.

  τη στιγμή t₁   η φορά του επαγωγικού ρεύματος είναι θετική   και  από το διάγραμμα φαίνεται ότι η ένταση του αυξάνεται  που σημαίνει ότι  δημιουργεί  μαγνητικό πεδίο ομόρροπο στο αρχικό  με την ένταση του να αυξάνεται   που σημαίνει ότι η ένταση του αρχικού μαγνητικού πεδίου  μειώνεται

  i_επαγ  =  I ημωt  =>  Β_επαγ  = 10^-7 2π i_επαγ /ρ  =>   Β_επαγ (t)  =  10^-7 2πΙ/ρ ημωt       

  i_επαγ = I ημωt  =  Ε_επαγ / R  =>  Ε_επαγ = IR ημωt  = - dΦ / dt  =>  dΦ  = - IR ημωt  dt   =>  Φ(t) = IR/ω συνωt    0<t<Τ/2          Φ(0) = IR/ω       Φ(Τ/4) = 0      Φ(Τ/2) = - IR/ω  

    t > Τ/2     i = 0   =>  Ε_επαγ = 0  =>  Φ = σταθερή   

..........................................................................................................................................................

Ο αγωγός ΑΓ μάζας  m = 0,1 kg, μήκους  l = 1 m  παρουσιάζει ωμική αντίσταση  r = 0,8 Ω  και μπορεί να κινείται σε επαφή με δύο μεταλλικούς κατακόρυφους στύλους, χωρίς αντίσταση, χωρίς τριβές.  Τα πάνω άκρα των δύο στύλων συνδέονται μέσω διακόπτη με ωμική αντίσταση  R,  ενώ στα κάτω άκρα συνδέουμε ένα ιδανικό βολτόμετρο.  Κάθετα στο επίπεδο του σχήματος υπάρχει ομογενές μαγνητικό πεδίο εντάσεως  Β = 1 Τ.  Με ανοικτό τον διακόπτη δ  κάποια στιγμή  t = 0,  αφήνουμε τον αγωγό ΑΓ να πέσει  και τη στιγμή  t = 0,5s  κλείνουμε τον διακόπτη.  Στο διάγραμμα φαίνεται η ένδειξη του βολτομέτρου, όπου πρακτικά τη στιγμή  t = 1,5s  έχει σταθεροποιηθεί η ένδειξή του.

Α)  Εξηγήστε τη μορφή της  γραφικής παράστασης της τάσης από  0 - 0,5s  και υπολογίστε την αντίσταση  R.

Β)  Βρείτε την επιτάχυνση του αγωγού ΑΓ  αμέσως μετά το κλείσιμο του διακόπτη  καθώς και τον ρυθμό μεταβολής της κινητικής ενέργειας τις στιγμές που το βολτόμετρο δείχνει ένδειξη 2 V.  

Γ)  Ποιά είναι η ένδειξη του βολτομέτρου τη στιγμή  t = 1,5s.

ελεύθερη πτώση αγωγού ΑΓ :   h = 0,5  g t²  =  0,5  10  0,5²  =  0,0125 m         v₀  =  g t =  10 0,5  =  5 m/s    

   Ε_επαγ   =  Β l v  =  B l g t      

  V  =  V_ΓΑ  = V_πολική  =  Ε_επαγ  - i r  => V  = B l g t  - i r  => 3V  = 1T  1m  5m/s  -  i  0,8Ω    =>  i  =  2/0,8 A =  2,5 A   

από 0  έως  0,5s   το βολτόμετρο δείχνει την  ΗΕΔ  δηλαδή την  Ε_επαγ  διότι το κύκλωμα είναι ανοικτό   έτσι  η ένδειξη του βολτομέτρου μεταβάλλεται  από  0  έως  5V 

όταν κλείνει ο διακόπτης δ  το κύκλωμα διαρρέεται από ρεύμα  έχουμε :  Ε_επαγ  =  i ( R + r )      

τότε    V  =  V_ΓΑ  = V_πολική  =  Ε_επαγ  - i r  =  i R  =>  3V = 2,5A R  =>  R = 1,2 Ω

 άλλος τρόπος   Ε_επαγ  =  i ( R + r )  =  V/R  ( R + r )  =>  Ε_επαγ  =  V  ( 1 + r/R )  =>   5V  =  3V  ( 1 + 0,8Ω/R )  =>

                                                    =>    5V  -  3V = 3V  0,8Ω/R   =>  R = 2,4/2 Ω = 1,2 Ω             

από  0 - 0,5s  :   V  =  Ε_επαγ  =  Β l v  =  B l g t   =  10 t  

                     όταν το βολτόμετρο δείχνει 2 V  έχουμε :   2 V = 10 t  =>  t = 0,2s    =>  v = g t = 10  0,2 = 2 m/s    

              ο ρυθμός μεταβολής της κινητικής ενέργειας τότε είναι :  dK/dt  =  m v g  =  0,1 kg  2 m/s  10 m/s²   =  2 J/s

  t > 0,5s  :     ΣF = m a  =>  m g  -  F_L  =  m a                    Ε_επαγ  =  i ( R + r )              Ε_επαγ   =  Β l v

                     i  =  Ε_επαγ / ( R + r )  =  B l v / (R+r)   (1)            F_L  =  B l  i  = B² l² v / (R+r)  

      m g  -  F_L  =  m a  =>   m g  -  B² l² v / (R+r)  =  m a  =>   1  -  1² 1² v / 2  =  0,1 a  =>  1  -  v/2  =  0,1 a   (2)     

 τη στιγμή που ο διακόπτης δ  κλείνει  η ράβδος έχει αποκτήσει ταχύτητα   v₀  =  g t =  10 0,5  =  5 m/s  

 οπότε  η (2) =>  1  -  5/2  =  0,1 α  =>  α  =  - 15 m/s²    αρχική επιτάχυνση

όταν η τάση   V = 2V  =>  i R  =  2V  =>  i  =  2V / 1,2Ω  =  20/12 = 5/3 A ,  

 η (1) => i  =  B l v / (R+r)  =>    5/3  =  1  1 v / 2   =>  υ  =  10/3 m/s      

και  η (2) => 1  -  (10/3)/2  =  0,1 α  =>   1  -  5/3  =  0,1 α  =>   α  =  - 20/3 m/s²      ο ρυθμός μεταβολής της κινητικής ενέργειας τότε είναι :  dK/dt  =  m v a  =  0,1 kg  10/3 m/s  (- 20/3 m/s² )  =  - 20/9 J/s

τη στιγμή  t = 1,5s  η τάση στα άκρα του βολτομέτρου έχει σταθεροποιηθεί,  η ράβδος έχει αποκτήσει την οριακή ταχύτητα  διότι η επιτάχυνση έχει μηδενισθεί   α = 0  =>  ⁽²⁾  1  -  υ/2 = 0  =>  υ = 2 m/s   =  υ_οριακή    

 τότε   η (1) =>   i  =  B l v / (R+r)  =>   i  =  1 1 2 / 2  = 1 Α  

 οπότε   η τάση του βολτομέτρου είναι :  V = i R  =  1 A  1,2 Ω   =  1,2 V  

    (2) =>  1  -  v/2  =  0,1  dv/dt  =>    - 1/2 ( v - 2 )  =  0,1  dv/dt  =>   dv / (v - 2) = - 5 dt   =>

         =>  ln [ (v - 2)/(5 - 2) ]  = - 5 (t - 0,5)    =>  v(t)  =  2 + 3 e^{-5 (t - 0,5)}      t > 0,5s        

  a = dv/dt =>  a(t)  =  - 15 e^{-5 (t - 0,5)}        t > 0,5s

  v = dx/dt  =>  dx  =  v dt  = ( 2 + 3 e^{-5 (t - 0,5)} ) dt  =>  x(t)  =   0,0125 +  2(t - 0,5)  - 0,6 ( e^{-5 (t - 0,5)} - 1 )     t > 0,5s

   t = 0,5s     v = 2 + 3 = 5 m/s          a = - 15 m/s²      x = 0,0125 m = h    

   t ® ¥       v = 2 m/s                       a = 0          x = 0,0125 + 2(t - 0,5) - 0,2 (-1) =  0,0125 + 2t - 1 + 0,2 = 2t - 0,7875  (m)

  t = 1,5s    v = 2 + 3 e^-5  = 2 m/s       a = - 15 e^-5 = 0        x = 0,0125 + 2(1,5 - 0,5)  - 0,2 ( e^-5 - 1 ) =  0,0125 + 2  - 0,2 (-1)  = 2  + 0,2 + 0,0125  =  2,2125 m  

                       i  =  Ε_επαγ / ( R + r )  =  B l v / (R+r)  =>   i(t)  =  v/2 =  0,5 ( 2 + 3 e^{-5 (t - 0,5)} ) = 1 + 1,5 e^{-5 (t - 0,5)}    

                    F_L  =  B l  i  = 1 + 1,5 e^{-5 (t - 0,5)}    >  1  =   m g    για αυτό το λόγο έχουμε επιβράδυνση    τη στιγμή που κλείνει ο διακόπτης δ  το κύκλωμα διαρρέεται από ρεύμα  και  η δύναμη Laplace έχει μέτρο μεγαλύτερο του βάρους          η ράβδος θα κάνει επιβραδυνόμενη κίνηση μέχρι να μηδενισθεί  η  α  ( διότι το μέτρο της επιβράδυνσης μειώνεται )  οπότε  η ταχύτητα της θα αποκτήσει σταθερή τιμή  ( υ_οριακή )

  V = R i =  1,2 ( 1 + 1,5 e^{-5 (t - 0,5)} )  =  1,2  + 1,8 e^{-5 (t - 0,5)}    τάση βολτομέτρου

  t = 0,5s :  V = 1,2  + 1,8 = 3 V  

 t = 1,5s  :   V(1,5)  =  1,2  + 1,8 e^{-5 (1,5- 0,5)}  =  1,2  + 1,8 e^-5  =  1,2 V    σταθεροποιήται η τάση

 όταν η τάση είναι   V = 2V  =>    1,2  + 1,8 e^{-5 (t - 0,5)}  = 2  =>  0,8  =  1,8 e^{-5 (t - 0,5)}  =>   e^{-5 (t - 0,5)}  =  8/18 = 4/9       

      v  =  2 + 3 e^{-5 (t - 0,5)} =  2 + 3 4/9 = 10/3 m/s 

       a  =  - 15 e^{-5 (t - 0,5)}  =  - 15 4/9  =  -20/3 m/s²         

 αν απομακρύνουμε τον διακόπτη και την αντίσταση  και τα πάνω άκρα συνδεθούν με σύρμα αμελητέας αντίστασης : 

επαγωγική τάση στη ράβδο ΑΓ :   Ε_επαγ   =  Β l v        

  νόμος του Ohm :    Ε_επαγ  = i r  =>  B l v  =  i r   =>   i  =  Blv / r            F_L  =  B l i  = B² l² v / r  

ΣF = m a  =>  m g  -  F_L  =  m a   =>   m g  - B² l² v / r  =  m a   =>   1  -  1 1 v / 0,8  =  0,1 a =>   1  -  5/4 v  =  0,1 a =>   10  -  12,5 v  =  a            

  V  =  V_ΓΑ  = V_πολική  =  Ε_επαγ  - i r  => V  =  0

10  -  12,5 v  =  a    =>      -  12,5 ( v - 0,8 )  =  dv/dt    =>  dv / ( v - 0,8 ) = - 12,5 dt  =>  ln [ ( v - 0,8 ) / (- 0,8) ] = - 12,5 t  =>    v(t)  =  0,8  - 0,8 e^{-12,5 t}                          a(t)  =  10 e^{-12,5 t}        

  i(t)  = B l v / r  =  1 - e^{-12,5 t}                     F_L (t) =  B l i(t)  =  1 - e^{-12,5 t}    

...........................................................................................................................................................................

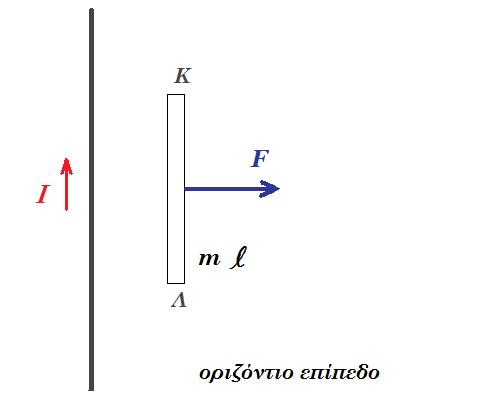Ευθύγραμμος αγωγός απείρου μήκους που βρίσκεται ακίνητος πάνω σε οριζόντιο επίπεδο διαρρέεται από ρεύμα εντάσεως  Ι.  Μεταλλική ράβδος παράλληλη στον αγωγό μάζας m και μήκους l  δέχεται στο μέσον της σταθερή οριζότια δύναμη F  κάθετη στη ράβδο, έτσι ώστε η ράβδος να κινείται παράλληλα στον ευθύγραμμο ρευματοφόρο αγωγό με σταθερή ταχύτητα μέτρου υ.   Δείξτε ότι στα άκρα της ράβδου αναπτύσσεται διαφορά δυναμικού.

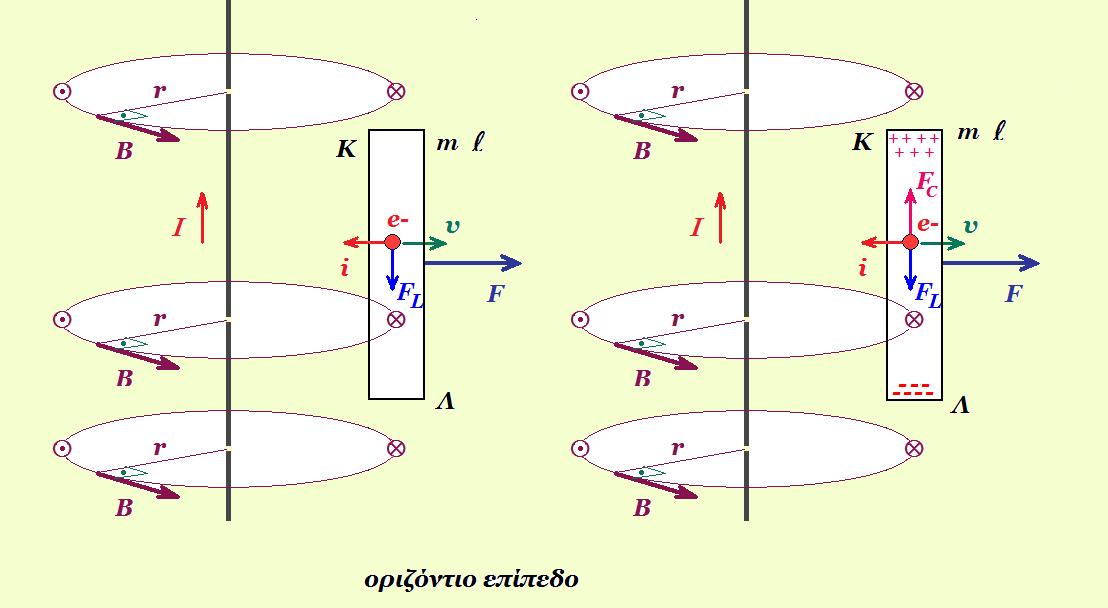
ο απείρου μήκους ευθύγραμμος  ρευματοφόρος αγωγός δημιουργεί στο χώρο γύρω του μαγνητικό πεδίο  οι δυναμικές γραμμές του οποίου είναι ομόκεντροι κύκλοι  τα επίπεδα των οποίων είναι κάθετα στον αγωγό,   σε απόσταση r η ένταση του πεδίου δίνεται από τη σχέση :  Β = 10^-7 2Ι/r    

καθώς κινείται η ράβδος μέσα στο μαγνητικό πεδίο που δημιουργεί ο αγωγός, τα ηλεκτρόνιά της δέχονται δύναμη Lorentz  F_L = q_e v B   όπου  υ  η ταχύτητα του ηλεκτρονίου  που ισούται με την ταχύτητα της ράβδου,   με συνέπεια να κατευθύνονται στο ένα άκρο της ράβδου Λ  το οποίο φορτίζεται αρνητικά  οπότε το άλλο άκρο Κ φορτίζεται θετικά  έτσι αναπτύσσεται διαφορά δυναμικού (τάση V_ΚΛ) στα άκρα Κ, Λ της ράβδου,         με συνέπεια  να δημιουργηθεί  ηλεκτρικό  πεδίο  εντάσεως  Ε = V_ΚΛ / l     

τα ηλεκτρόνια της ράβδου τώρα δέχονται και  δύναμη Coulomb  από το ηλεκτρικό πεδίο :  F_C = E q_e       οι δυνάμεις  Coulomb  και  Lorentz  είναι αντίρροπες   

όσο κινείται η ράβδος μέσα στο μαγνητικό πεδίο  συσσωρεύονται περισσότερα ηλεκτρόνια στο άκρο Λ  και  "αδειάζει" η περιοχή του άκρου Κ  οπότε αυξάνεται η διαφορά δυναμικού V_ΚΛ   άρα αυξάνεται η ένταση Ε  του ηλεκτρικού πεδίου  άρα αυξάνεται το μέτρο της δύναμης Coulomb   με συνέπεια οι δυνάμεις  Coulomb  και  Lorentz  να γίνουν αντίθετες  

    F_C = F_L   =>   E q_e = q_e v B  =>  Ε = υ Β   =>  V_ΚΛ / l = υ Β  =>   V_ΚΛ  = Β l υ    

   τελικά :   V_ΚΛ  = 10^-7 2Ι l υ / r  

για την κίνηση της ράβδου έχουμε :  ΣF  =  m a  =>  F - Τ_τριβές  =  0  διότι  υ = σταθερή      

...............................................................................................................................................

Ευθύγραμμος αγωγός απείρου μήκους που βρίσκεται ακίνητος πάνω σε οριζόντιο επίπεδο διαρρέεται από ρεύμα εντάσεως  Ι.  Μεταλλικό ορθογώνιο πλαίσιο ΚΛΜΝ  με διαστάσεις  ΚΛ = ΜΝ =  l  και  ΚΝ = ΛΜ =  d ,   η  ΚΛ παράλληλη στον αγωγό,  μάζας m   και ωμικής αντίστασης R  δέχεται στο μέσον της πλευράς ΚΛ  σταθερή οριζότια δύναμη F  κάθετη στη ΚΛ, έτσι ώστε το πλαίσιο να κινείται παράλληλα στον ευθύγραμμο ρευματοφόρο αγωγό με σταθερή ταχύτητα μέτρου υ.  

Δείξτε ότι το πλαίσιο διαρρέεται από ρεύμα.

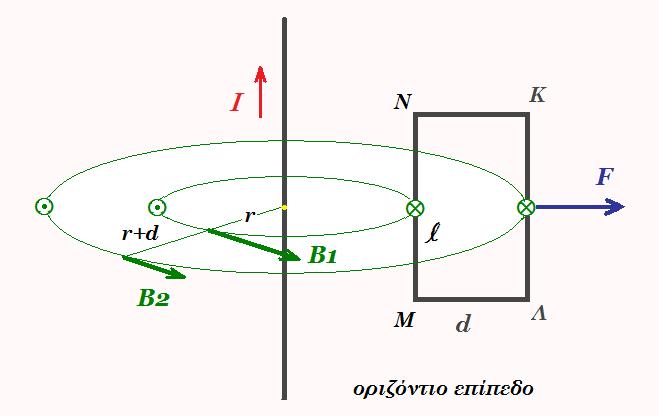
για την κίνηση του πλαισίου έχουμε :  ΣF  =  m a  =>  F - Τ_τριβές  =  0  διότι  υ = σταθερή      

στην πλευρά ΚΛ  του πλαισίου αναπτύσσεται τάση  V_ΚΛ  = υ Β₂ l  = 10^-7 2Ι l υ / (r+d)      

στην πλευρά ΜΝ  του πλαισίου αναπτύσσεται τάση  V_ΝΜ  = υ Β₁ l  = 10^-7 2Ι l υ / r    

συνολικά  Ε_επαγ  = V_ΝΜ  - V_ΚΛ =  10^-7 2Ι l υ / r   -  10^-7 2Ι l υ / (r+d)  =   10^-7 2Ι l υ ( 1/r - 1/(r+d) )  

          =>   Ε_επαγ  =  10^-7 2Ι l d υ / (r+d)r      

    i_επαγ  = Ε_επαγ / R  =  10^-7 2Ι l d υ / (r+d)rR     ένταση επαγωγικού ρεύματος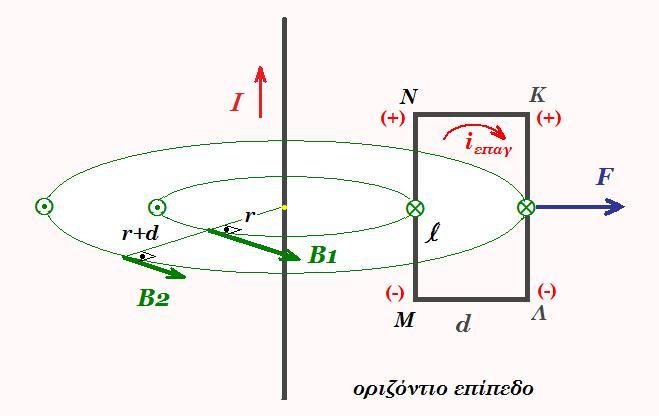     

...................................................................................................................................................................

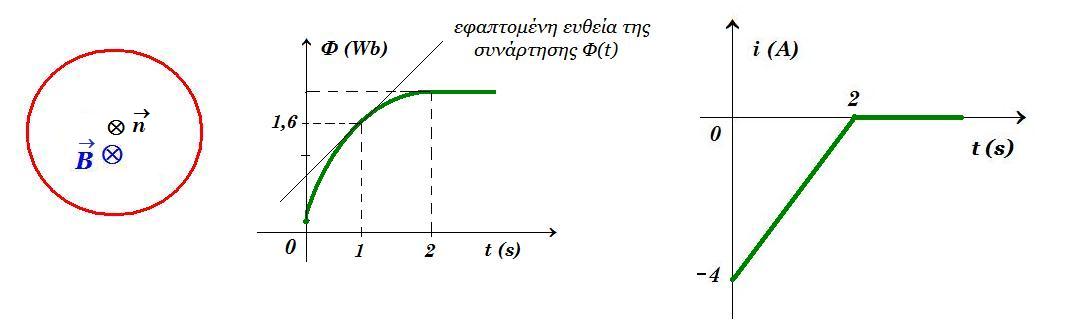
Αγώγιμο κυκλικό πλαίσιο με ωμική αντίσταση  R = 0,5 Ω  βρίσκεται μέσα σε μαγνητικό πεδίο με το επίπεδό του κάθετο στις δυναμικές γραμμές.  Στο σχήμα φαίνεται η μαγνητική ροή που διέρχεται από το επίπεδο του πλαισίου συναρτήσει του χρόνου   και  η μεταβολή της τιμής της έντασης του ρεύματος που διαρρέει το πλαίσιο  λόγω επαγωγής.  

α)  Υπολογίστε τον στιγμιαίο ρυθμό μεταβολής της μαγνητικής ροής τις χρονικές στιγμές  t=0  και  t = 1s

β)  Πόσο φορτίο πέρασε από μια διατομή του αγωγού στο χρονικό διάστημα  0 - 1s. 

γ)  Υπολογίστε την αρχική μαγνητική ροή ( =0) που διέρχεται από το επίπεδο του  πλαισίου  καθώς και ο μέσος ρυθμός μεταβολής της μαγνητικής ροής στο χρονικό διάστημα  0 - 1s.

   Φ  =  Β Α              i =  a t + b  =  2t - 4          

  t = 0    i = -4A     Ε_επαγ = i R = -4 . 0,5 = -2V = - dΦ/dt  =>   dΦ/dt = 2V = Φ'(0)    κλίση της ευθείας της εξίσωση εφαπτομένης στο σημείο t = 0  

εξίσωση εφαπτομένης στο σημείο t = 0 :   y  -  Φ(0)  =  Φ'(0)  (t - 0)   =>   y - 0 = 2 t   =>  y = 2t

  t = 1s    i = -2A     Ε_επαγ = i R = -2 . 0,5 = -1V  =  - dΦ/dt  =>   dΦ/dt = 1V = Φ'(1)    κλίση της ευθείας της εξίσωση εφαπτομένης στο σημείο t = 1s

εξίσωση εφαπτομένης στο σημείο t = 1s :    y  -  Φ(1)  =  Φ'(1)  (t - 1)   =>    y  -  1,6  =  1 (t - 1)  =>   y =  t - 1 + 1,6  =>   y  =  t + 0,6

 όταν  t  ³  2s    έχουμε   i = 0     οπότε   Ε_επαγ = i R  = 0 =  - dΦ/dt  =>  Φ = σταθερή  

  i = dq/dt  =>  dq  =  i dt  =  (2t - 4) dt  =  2t dt  -  4 dt  =>  q_{(t=0 , t=1s)}  =  [ t²  -  4t  ]_{(t=0 , t=1s)}  =  (1 - 0)²  -  4 (1 - 0)  = 1 - 4 = - 3 Coulomb     

  t = 0   i(0) = - 4A   

    άλλος τρόπος  από το εμβαδόν του χωρίου (τραπεζίου) :  q = (4 + 2) (1 - 0) / 2  =>  q = 3 Coulomb

   0 £  t  £  1s        |Δq| = ΔΦ / R  =>  |Δq| = [ Φ(1) - Φ(0) ] / R  =>      3 = [ 1,6 - Φ(0) ] / 0,5  =>   1,5  =  1,6  -  Φ(0)  =>  Φ(0)  =  0,1 Wb

   ΔΦ / Δt  =  ( Φ(1) - Φ(0) ) / ( 1 - 0 )  =  ( 1,6 - 0,1 ) / 1  =  1,5 Wb/s  = 1,5 Volt

    Ε_επαγ  = i R  =>   - dΦ / dt  =  (2t - 4)  0,5   =>  dΦ / dt  =  - t + 2   =>

dΦ  =  ( - t + 2 ) dt   =>  Φ (t)  =  - 0,5 t² + 2t + c   

επειδή  Φ (0)  =  0,1  =>   -0,5 0² + 2 0 + c  = 0,1  =>  c = 0,1     τελικά    Φ (t) = -0,5 t² + 2t + 0,1         

Φ (1)  =   -0,5 1² + 2 . 1 + 0,1 =  -0,5 + 2 + 0,1 = 1,6 Wb 

Φ (2)  =   -0,5 2² + 2 . 2 + 0,1 = -0.5 4  + 4 + 0,1 = 2,1 Wb 

                   τελικά έχουμε :

   Φ(t) = - 0,5 t² + 2t + 0,1           Ε_επαγ(t) = - Φ'(t) = t - 2          i_επαγ(t) = Ε_επαγ(t) / R = - 2t + 4           

---------------------------------------------------------------------------------------------------------------------------------------------

Αγώγιμο κυκλικό πλαίσιο με ωμική αντίσταση  R = 0,5 Ω  βρίσκεται μέσα σε μαγνητικό πεδίο με το επίπεδό του κάθετο στις δυναμικές γραμμές.  Στο σχήμα φαίνεται η μαγνητική ροή που διέρχεται από το επίπεδο του πλαισίου συναρτήσει του χρόνου.

 Υπολογίστε την  ΗΕΔ  που εμφανίζεται στο πκαίσιο  για το χρονικό διάστημα  0 - 3s.  

Να σχεδιάστε τη γραφική περάσταση της έντασης του ρεύματος που διαρρέει το πλαίσιο για το χρονικό διάστημα  0 - 3s.  

Βρείτε πόσο φορτίο πέρασε από μια διατομή του πλαισίου στο χρονικό διάστημα  0 - 3s.

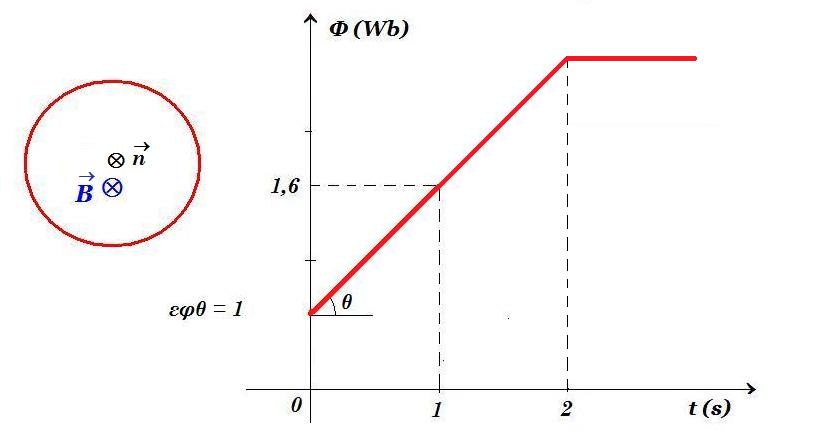
από το διάγραμμα φαίνεται ότι  η μαγητική ροή είναι συνάρτηση 1ου βαθμού ως προς τον χρόνο    Φ(t) = α t + β  με κλίση  εφθ = 1 = α     ενώ η γραφική παράσταση διέρχεται από το σημείο  ( 1s , 1,6Wb )   οπότε έχουμε :  Φ(t) = α t + β  =>  Φ(1) = 1 1 + β = 1,6  =>  β = 0,6 Wb    τελικά :  Φ(t) =  t + 0,6     Φ σε Wb , t σε s       για   0 £  t  £  2s  

    Φ(0) =  0 + 0,6 = 0,6 Wb     Φ(2) =  2 + 0,6  =  2,6 Wb   

στο πλαίσιο εμφανίζεται επαγωγική τάση  Ε_επαγ = - ΔΦ/Δt  = - ( 2,6 - 0,6 ) / ( 2 - 0 ) = - 1 V

από τον νόμο του Ohm :  i =  Ε_επαγ / R = - 1V / 0,5Ω  = - 2 Α    σταθερό    από  0   έως  2s

  όταν    t > 2s    η μαγνητική ροή είναι   Φ(2)  =  2,6 Wb  σταθερή  οπότε δεν επάγεται τάση στο πλαίσιο δηλαδή Ε_επαγ = 0   οπότε  η ένταση του επαγωγικού ρεύματος είναι  μηδέν    

στο χρονικό διάστημα  0 - 2s   η ένταση του επαγωγικού ρεύματος είναι  2Α   οπότε περνά φορτίο   q  =  i t  =  2A 2s = 4 C

στο χρονικό διάστημα  2s - 3s   η ένταση του επαγωγικού ρεύματος είναι  i = 0   οπότε περνά φορτίο   q  =  i t  =  0 C

................................................................................................................................................................

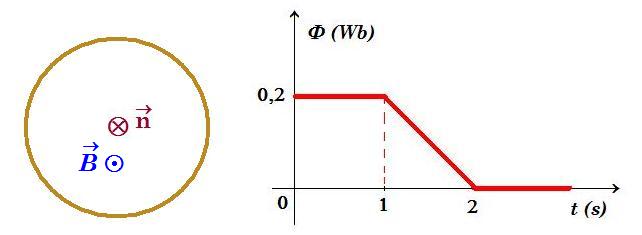
Αγώγιμο κυκλικό πλαίσιο με εμβαδόν επιφάνειας Α = 1 m²  και ωμική αντίσταση  R = 2 Ω,  βρίσκεται μέσα σε μαγνητικό πεδίο με το επίπεδό του κάθετο στις δυναμικές γραμμές του.  Στο σχήμα  έχει σχεδιαστεί η κάθετος στο επίπεδο του αγωγού   ενώ στο διάγραμμα δίνεται  η γραφική παράσταση της μαγνητικής ροής που διέρχεται από το επίπεδο του πλαισίου συναρτήσει του χρόνου.

Βρείτε την ένταση του μαγνητικού πεδίου.

Βρείτε την  ΗΕΔ  που εμφανίζεται στο πλαίσιο  σε συνάρτηση με τον χρόνο. 

Πόση θερμότητα παράγεται πάνω στον αγωγό   και  πόσο φορτίο διέρχεται από μια διατομή του ;   

Αν η μεταβολή της ΗΕΔ που αναπτύσσεται στο πλαίσιο συναρτήσει του χρόνου είναι όπως στο διάγραμμα  Ε(t)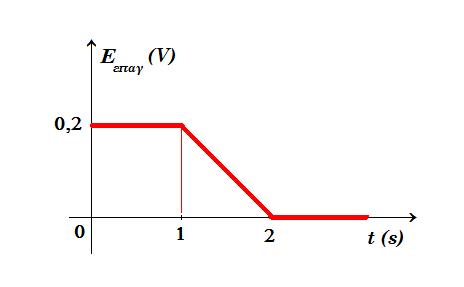   

Βρείτε τη μαγνητική ροή που διέρχεται από το επίπεδο του πλαισίου στο χρονικό διάστημα  0 - 3s.  

Σχεδιάστε τη γραφική περάσταση της μαγνητικής ροής που διέρχεται από το επίπεδο του πλαισίου συναρτήσει του χρόνου  καθώς και του μαγνητικού πεδίου.

Βρείτε πόσο φορτίο περνά από μια διατομή του αγωγού στο χρονικό διάστημα  0 - 3s.  

Ποιο από τα παρακάτω ποιοτικά διαγράμματα  θα μπορούσε να παριστά  την μαγνητική ροή που διέρχεται από το επίπεδο του πλαισίου  συναρτήσει του χρόνου ;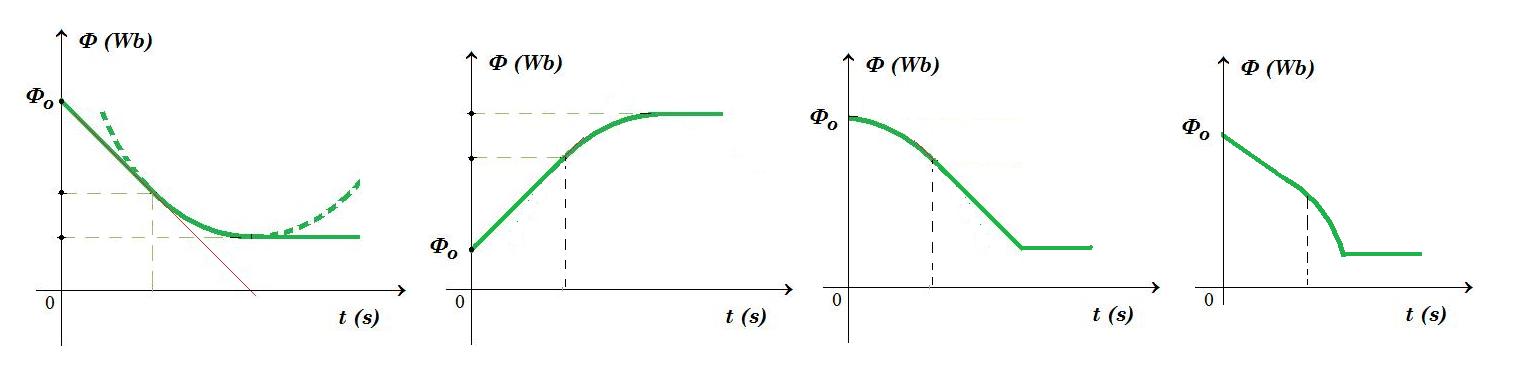 

  από το διάγραμμα Φ(t)  φαίνεται ότι η μαγνητική ροή που διέρχεται μέσα από το επίπεδο του πλασίου είναι θετική   οπότε  Φ = Β Α συν180°  =  - Β Α  =>  Β = - Φ / Α  

στο χρονικό διάστημα  0 - 1s  η μαγνητική ροή είναι σταθερή  Φ = 0,2 Wb    οπότε η επαγωγική τάση είναι  μηδέν   οπότε  η ένταση του επαγωγικού ρεύματος είναι  μηδέν  

                    Φ = - Β Α  =>    0,2 Wb  =  - Β  1 m²  =>  B = - 0,2 Tesla      

στο χρονικό διάστημα  1s - 2s   η μαγνητική ροή είναι   Φ(t) = - 0,2 t + 0,4     =>   Ε_επαγ = - dΦ/dt  =  + 0,2 Volt      =>     i_επαγ = Ε_επαγ / R  =  +2V / 2Ω  = +1Α    σταθερό  

          Φ = - Β Α  => - 0,2 t + 0,4  =  - Β  1 m²  =>  B =  +0,2 t - 0,4

όταν    t > 2s    η μαγνητική ροή είναι   Φ  =  0   ( άρα  Β = 0 )   οπότε δεν επάγεται τάση στο πλαίσιο δηλαδή Ε_επαγ = 0   οπότε  η ένταση του επαγωγικού ρεύματος είναι  μηδέν    

η θερμότητα που αναπτύσσεται πάνω στον αγωγό  είναι μόνο στο χρονικό διάστημα  1s - 2s  :    Q_θερμ  =  i² R t  =  1² 2 1  =  2 Joule         στο διάστημα αυτό  από μια διατομή του πλαισίου περνά φορτίο   q  =  i t  =  1A  1s  = 1 C

                              ...............................................................................................

  έστω τη χρονική στιγμή t = 0   η μαγνητική ροή ισούται με :   Φ = Φ₀     

  Ε_επαγ  = - dΦ/dt  =>   dΦ  = - Ε_επαγ  dt      

 από το εμβαδόν του χωρίου (τραπεζίου) έχουμε  ΔΦ  =  εμβαδόν τραπεζίου = (1 + 2) 0,2 / 2 =   0,3 Wb  

 0 £  t  £  1s  :    Ε_επαγ  =  +0,2V   =>    dΦ  = - Ε_επαγ  dt   =>  Φ(t)  =  Φ₀  - 0,2 t ,        Φ(0) = Φ₀ ,   Φ(1) = Φ₀  - 0,2 Wb       

1s £  t  £  2s  :   Ε_επαγ  = - 0,2 t + 0,4    =>   dΦ  = - Ε_επαγ  dt  =>   dΦ  = - ( - 0,2 t + 0,4 ) dt  =>   dΦ  =  ( 0,2 t - 0,4 ) dt      =>   dΦ  =  0,2 t dt  -  0,4 dt   =>    Φ(t)  =  0,1 t²  -  0,4 t  + c           

     επειδή  Φ(1)  = Φ₀  - 0,2 Wb  =  0,1 1²  -  0,4 1  + c  =>  Φ₀  - 0,2  - 0,1   +  0,4   =  c  =>   c = Φ₀  + 0,1 , 

                                                                           άρα   Φ(t)  =  0,1 t²  -  0,4 t  + Φ₀ + 0,1   

                    Φ(1) =  0,1 1² - 0,4 1 + Φ₀  + 0,1  =  0,1 - 0,4 +Φ₀  + 0,1 = Φ₀ - 0,2 Wb    και  

                    Φ(2) = 0,1 2² - 0,4 2 +Φ₀  + 0,1  = 0,4 - 0,8 + Φ₀  + 0,1 = Φ₀  - 0,3Wb 

 για  t  ³  2s :    Ε_επαγ  =  0   =>   Φ(t)  =  σταθερή  = Φ(2)  = Φ₀ - 0,3 Wb  

εξίσωση εφαπτομένης  της συνάρτησης   Φ(t)  =  0,1 t²  -  0,4 t  + Φ₀ + 0,1        Φ'(t)  =  0,2 t  -  0,4 , στο σημείο  ( 1 , Φ(1) ) 

        Φ(1)  =  0,1 1²  -  0,4 1 + Φ₀ + 0,1 =   Φ₀ - 0,2       Φ'(1)  =  0,2 1  -  0,4 = - 0,2       

    y  -  Φ(1)  =  Φ'(1)  ( t - 1 )  =>     y  - (Φ₀ - 0,2)  =  - 0,2  ( t - 1 )  =>  y = Φ₀ - 0,2 t     

εξίσωση εφαπτομένης  της συνάρτησης   Φ(t)  =  0,1 t²  -  0,4 t  + Φ₀ + 0,1        Φ'(t)  =  0,2 t  -  0,4 , στο σημείο  ( 3 , Φ(3) ) 

        Φ(3)  =  0,1 3²  -  0,4 3 + Φ₀ + 0,1 =   Φ₀ - 0,2       Φ'(3)  =  0,2 3  -  0,4 = + 0,2      

    y  -  Φ(3)  =  Φ'(3)  ( t - 3 )  =>     y  - (Φ₀ - 0,2)  =  + 0,2  ( t - 3 )  =>  y = + 0,2 t  + Φ₀  - 0,8  

εξίσωση εφαπτομένης  της συνάρτησης   Φ(t)  =  0,1 t²  -  0,4 t  + Φ₀ + 0,1        Φ'(t)  =  0,2 t  -  0,4 , στο σημείο  ( 2 , Φ(2) ) 

        Φ(2)  =  0,1 2²  -  0,4 2 + Φ₀ + 0,1 =   Φ₀ - 0,3       Φ'(2)  =  0,2 2  -  0,4 = 0       

    y  -  Φ(2)  =  Φ'(2)  ( t - 2 )  =>     y  - (Φ₀ - 0,3)  =  0 ( t - 2 )  =>  y = Φ₀ - 0,3

η μαγνητική ροή που διέρχεται από το επίπεδο του πλαισίου στο χρονικό διάστημα  0 - 3s  είναι :

          |Φ_τελική  -  Φ_αρχική | =  |Φ₀ - 0,3 Wb  -  Φ₀ | =   0,3 Wb

επειδή  τα διανύσμα  Β  και n  είναι αντίρροπα  έχουμε για το μαγνητικό πεδίο:   Φ = - Β Α  =>  Β = - Φ / Α   

 0 £  t  £  1s  :     Φ(t)  =  Φ₀  - 0,2 t  =>   Β(t)  =   0,2 t  - Φ₀       A = 1 m²    

 1s £  t  £  2s  :   Φ(t)  =  0,1 t²  -  0,4 t  + Φ₀ + 0,1  =>  B(t)  = -  0,1 t²  +  0,4 t  - Φ₀ - 0,1      

 για  t  ³  2s :     Φ(t)  =  σταθερή  = Φ(2)  = Φ₀ - 0,3 Wb  =>  B(t)  =  0,3 - Φ₀      

για να βρούμε το φορτίο συναρτήσει του χρόνου έχουμε :   

 0 £  t  £  1s  :    Ε_επαγ  =  +0,2V   =>   i_επαγ  = Ε_επαγ / R  =  +0,2V/2Ω = + 0,1Α

      i  =  dq / dt  =>  dq  =  i dt  =  +0,1 dt  =>  q(t) = 0,1 t          q(0) = 0     q(1) = 0,1 C

1s £  t  £  2s  :   Ε_επαγ  = - 0,2 t + 0,4    =>   i_επαγ  = Ε_επαγ / R  =  ( - 0,2 t + 0,4 ) /2Ω  =>  i(t) = - 0,1 t + 0,2   

      i  =  dq / dt  =>  dq  =  i dt  =  ( - 0,1 t + 0,2 ) dt  =>  q(t) - q(1) = - 0,05 ( t² - 1² ) + 0,2 (t - 1)    =>

       =>   q(t) - 0,1 = - 0,05 t²  +  0,05  + 0,2 t  - 0,2   =>  q(t)  =  - 0,05 t²  +  0,2 t  - 0,05     q(1) = 0,1 C     q(2) = 0,15 C

 για  t  ³  2s :    Ε_επαγ  =  0   =>   i_επαγ  = 0   =>   q  =  q(2)  =  0,15 Coulomb    σταθερό   

εξίσωση εφαπτομένης  της συνάρτησης   q(t)  =  - 0,05 t² +  0,2 t  - 0,05 ,   q'(t)  = - 0,1 t  +  0,2  , στο σημείο  ( 1 , 0,1 ) 

        q(1)  =  - 0,05 1²  +  0,2 1  - 0,05 = - 0,05 + 0,2 - 0,05 => q(1) = 0,1          q'(1) = - 0,1 1 + 0,2 = 0,1  

    y  -  q(1)  =  q'(1)  ( t - 1 )  =>     y  -  0,1  =  0,1  ( t - 1 )  =>   y  =  0,1 t          

0 £  t  £  1s      i_επαγ = + 0,1 A         q = 0,1  1  = 0,1 C   

1s £  t  £  2s    i_επαγ (t)  = - 0,1 t + 0,2         q = | i(2) - i(1)| (2 - 1) / 2  = | 0 - 0,1| 1 / 2 = 0,05 C      

για  t  ³  2s :   i_επαγ =  0           συνολικά το φορτίο που περνά από μια διατομή του πλαισίου είναι :  0,1 C + 0,05 C = 0,15 C

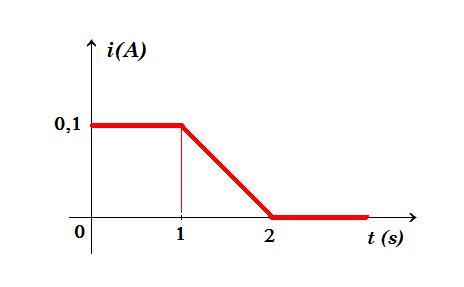 από το εμβαδόν του χωρίου (τραπεζίου) έχουμε   q  =  εμβαδόν τραπεζίου = (1 + 2) 0,1 / 2 =   0,15 Coulomb      

---------------------------------------------------------------------------------------------------------------------------------------------

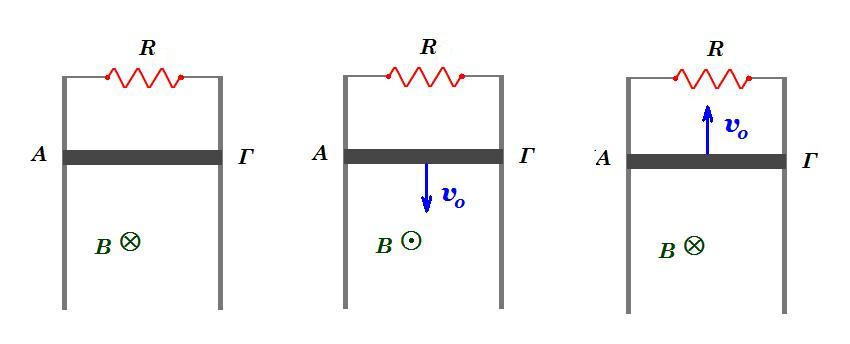
  Ε_επαγ  =  B l v            i  = Ε_επαγ / R  =  B l v / R                        F_L  =  B l i  = B² l² v / R   

  m g  -  F_L  =  m a  =>  m g  - B² l² v / R  =  m a   =>   B² l² v / R   -  m g   =   - m a   =>

        =>    B²l²/R  ( v -  m g R / B² l² )  =  - m dv/dt   =>    dv / ( v -  mgR / B²l² )  =  - B²l² / mR dt   =>

        =>    dv / ( v -  υ* )  =  - 1/τ dt   =>                                     mgR / B²l²  = υ*       B²l² / mR = 1/τ       v*/τ = g   

        =>     ln ( v - υ* )/( - v*)  =  - t/τ   =>   v - υ* = - v*  e^{- t/τ}   =>   v(t)  =  υ* ( 1 -  e^{- t/τ} )     a(t)  =  v*/τ  e^-t/τ > 0       

     v(0)  =  υ* ( 1 - 1 ) = 0               v(5τ)  =  υ* ( 1 -  e^{- 5τ/τ} ) =  υ*  =  mgR / B²l²   οριακή ταχύτητα   ( επιτάχυνση  α = 0 )

           U  =   m g (H - y)        

    dU/dt  = - m g dy/dt  =  - m g v  =  - m g υ* ( 1 - e^{- t/τ} )   =  - m  v*/τ  v* ( 1 - e^{- t/τ} )   =   -  m/τ  υ* ² ( 1 - e^{- t/τ})

       K  =  0,5 m v²                dK/dt  =  m v a  =  m  υ* ( 1 - e^{- t/τ} )   υ*/τ  e^{- t/τ}  =  m/τ  υ* ²  ( 1 - e^{- t/τ} )  e^{- t/τ}       

 F_L  =  B l i  = B² l² v / R  =  B²l²/R  υ* ( 1 - e^{- t/τ} )      

 P_FL =  F_L  v  =   B²l²/R  υ* ( 1 - e^{- t/τ} )  υ* ( 1 - e^{- t/τ} )  = B²l²/R  υ* ² ( 1 - e^{- t/τ} )² = m/τ  υ* ² ( 1 - e^{- t/τ} )²   

        dK/dt  + P_FL =  m/τ  υ* ²  ( 1 - e^{- t/τ} )  e^{- t/τ}  +   m/τ  υ* ² ( 1 - e^{- t/τ} )²   =  m/τ  υ* ² ( 1 - e^{- t/τ})   =  - dU/dt

                                             .................................................................................

  Ε_επαγ  =  B l v            i  = Ε_επαγ / R  =  B l v / R                        F_L  =  B l i  = B² l² v / R   

  m g  -  F_L  =  m a  =>  m g  - B² l² v / R  =  m a   =>   B² l² v / R   -  m g   =   - m a   =>

        =>    B²l²/R  ( v -  m g R / B² l² )  =  - m dv/dt   =>    dv / ( v -  mgR / B²l² )  =  - B²l² / mR dt   =>

        =>    dv / ( v -  υ* )  =  - 1/τ dt   =>                                                mgR / B²l²  = υ*       B²l² / mR = 1/τ

        =>     ln ( v - υ* )/( υ₀ - v*)  =  - t/τ   =>   v - υ* = ( υ₀ - v*) e^{- t/τ}    =>

        =>    v(t)  =  υ₀  + υ* ( 1 -  e^{- t/τ} )   a(t)  =  v*/τ  e^-t/τ  > 0

              v(0)  =  υ₀  + υ* ( 1 - 1 ) =  υ₀               v(5τ)  =  υ₀  + υ* ( 1 -  e^{- 5τ/τ} )  =  υ₀  + υ*  =  υ₀  + mgR / B²l²   οριακή ταχύτητα   ( επιτάχυνση   α  =  0 )                  

     U  =   m g (H - y)             dU/dt  = - m g dy/dt  =  - m g v  =  - m g  [ v₀  + υ* ( 1 - e^{- t/τ} ) ]

       K  =  0,5 m v²                 dK/dt  =  m v a  =  m   [ v₀  + υ* ( 1 - e^{- t/τ} ) ]   υ*/τ  e^{- t/τ}                

                                            ...........................................................................

Ε_επαγ  =  B l v            i  = Ε_επαγ / R  =  B l v / R                        F_L  =  B l i  = B² l² v / R   

 - m g  -  F_L  =  m a  =>  - m g  - B² l² v / R  =  m a   =>   - B²l²/R  ( v  +  m g R / B² l² )  =   m dv/dt   =>  

     =>   dv / ( v +  mgR / B²l² )  =  - B²l² / mR dt    =>    dv / ( v  +  υ* )  =  - 1/τ dt   =>                                                mgR / B²l²  = υ*       B²l² / mR = 1/τ

       =>     ln ( v + υ* )/( υ₀ + v*)  = - t/τ   =>   v + υ* = ( υ₀ + v*) e^-t/τ    =>  

      =>     v(t)  =  υ₀  + υ* ( - 1 + e ^-t/τ )    a(t)  =  - v*/τ  e^-t/τ  < 0 

        v(0)  =  v₀  +  v* ( - 1 + 1 ) =  v₀            v(5τ)  =  υ₀  + υ* ( - 1 + e ^-5τ/τ )  = υ₀  -  υ*  =   υ₀  -  mgR / B²l²     

     U  =   m g (H - y)             dU/dt  = - m g dy/dt  =  - m g v  =  - m g  [ v₀  + υ* ( - 1 + e^{- t/τ} ) ]

       K  =  0,5 m v²                 dK/dt  =  m v a  =  m   [ v₀  + υ* ( - 1 + e^{- t/τ} ) ]  [ - υ*/τ  e^{- t/τ} ]