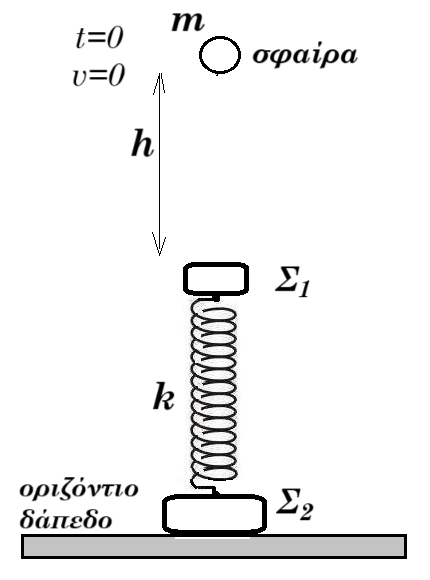
Στο σχήμα τα σώματα Σ₁  και Σ₂  με μάζες M₁ = 1 kg , M₂ = 3 kg αντίστοιχα  ισορροπούν ακίνητα δεμένα στα άκρα ιδανικού ελατηρίου σταθεράς  k = 100 N/m.  Σφαίρα μάζας m = 0,5 kg αφήνεται να πέσει τη στιγμή t = 0 από ύψος h = 1,8 m  πάνω από το Σ₁  Η σφαίρα συγκρούεται με το Σ₁  κεντρικά - ελαστικά.  

Α)  Ποιά είναι η μεταβολή της ορμής της σφαίρας κατά την κρούση;

Όταν η σφαίρα φθάσει σε μέγιστο ύψος  απομακρύνεται.

Β)  Εκφράστε την δύναμη Ν που δέχεται το σώμα Σ₂  από το οριζόντιο δάπεδο συναρτήσει του χρόνου.

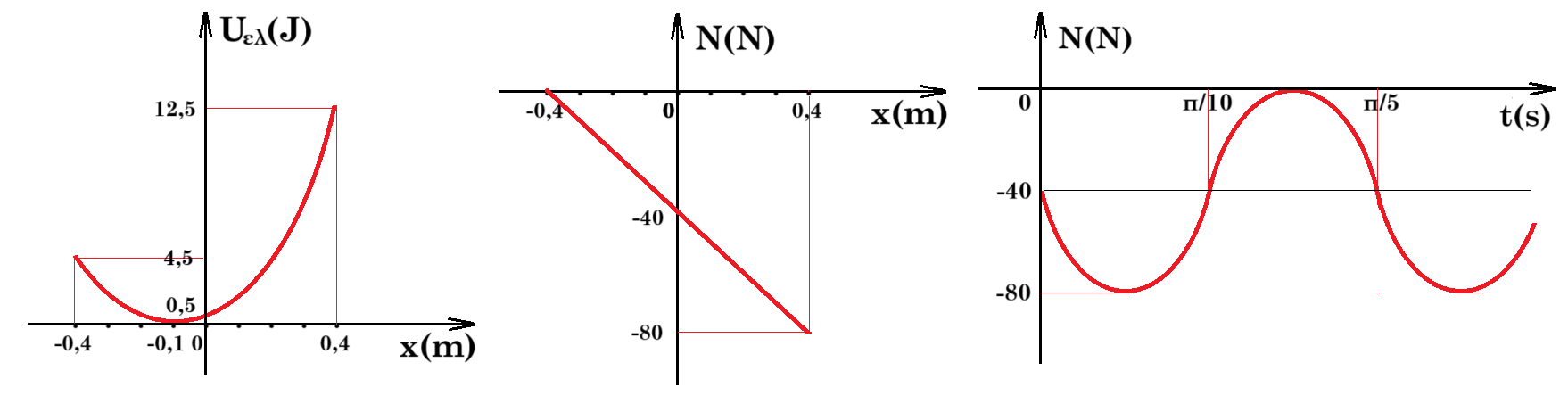
Γ)  Σχεδιάστε τα διαγράμματα   Ν(t) ,  Ν(x)  και  U_ελ (x)  σε βαθμολογημένους άξονες.

Θεωρούμε θετική κατεύθυνση την κατακόρυφη προς τα κάτω  και t=0 αρχή μέτρησης χρόνου για την ταλάντωση του Σ₁.

ισορροπία Σ₁ :  ΣF = 0  =>   M₁ g = k Δl  =>  10 = 100 Δl  =>  Δl = 0,1 m    συσπείρωση ελατηρίου

ελεύθερη πτώση σφαίρας :   m g h = 0,5 m v₀²  =>  g h = 0,5 v₀²  =>  10 1,8 = 0,5 v₀²  =>  v₀=6m/s  η ταχύτητα της σφαίρας πριν συγκρουστεί με το σώμα Σ₁ 

κεντρική ελαστική κρούση σφαίρας και Σ₁  έστω   v'  και  V₁  αντίστοιχα οι ταχύτητες τους αμέσως μετά την κρούση

  σφαίρα :  v'  =  v₀  (m - M₁) / (m + M₁)  =  6 (0,5 - 1) / (0,5 + 1)  = - 2 m/s  

 σώμα Σ₁ :  V₁  =  2 v₀ m / (m + M₁)  =  2 6 0,5 / 1,5 = + 4 m/s

η σφαίρα μετά την κρούση ανέρχεται σε ύψος  h' = (v')²/ 2g  =  4 / 20 =>  h' = 0,2 m  

μεταβολή της ορμής της σφαίρας : 

            Δp = p_μετά - p_πριν =  m v' - m v₀ = 0,5 (-2) - 0,5 6 = - 4 kg.m/s

το σώμα Σ₁  αμέσως μετά την κρούση βρίσκεται σε θέση όπου ΣF = 0 ,  έχει ταχύτητα +4 m/s  άρα είναι στη θέση ισορροπίας για την ταλάντωση   συνεπώς  θα εκτελέσει ΑΑΤ  με μέγιστη ταχύτητα  + 4 m/s  και κυκλική συχνότητα   ω² = k / M₁ = 100 / 1 =>  ω = 10 rad/s

διατήρηση ενέργειας για την ταλάντωση :  0,5 M₁ V₁²  =  0,5 k A²  =>  16 = 100 A² => A=0,4m   πλάτος ταλάντωσης του Σ₁  

         x(t) = 0,4  ημ(10.t)            v(t) = 4 συν(10.t)                  α(t) = - 40 ημ(10.t)   

ΣF = M₁ a = - 40 ημ(10.t)   

ΣF = M₁ a =>  M₁ g  +  F_ελ  = Μ₁ α   =>  10  + F_ελ  =  - 40 ημ(10.t)  =>

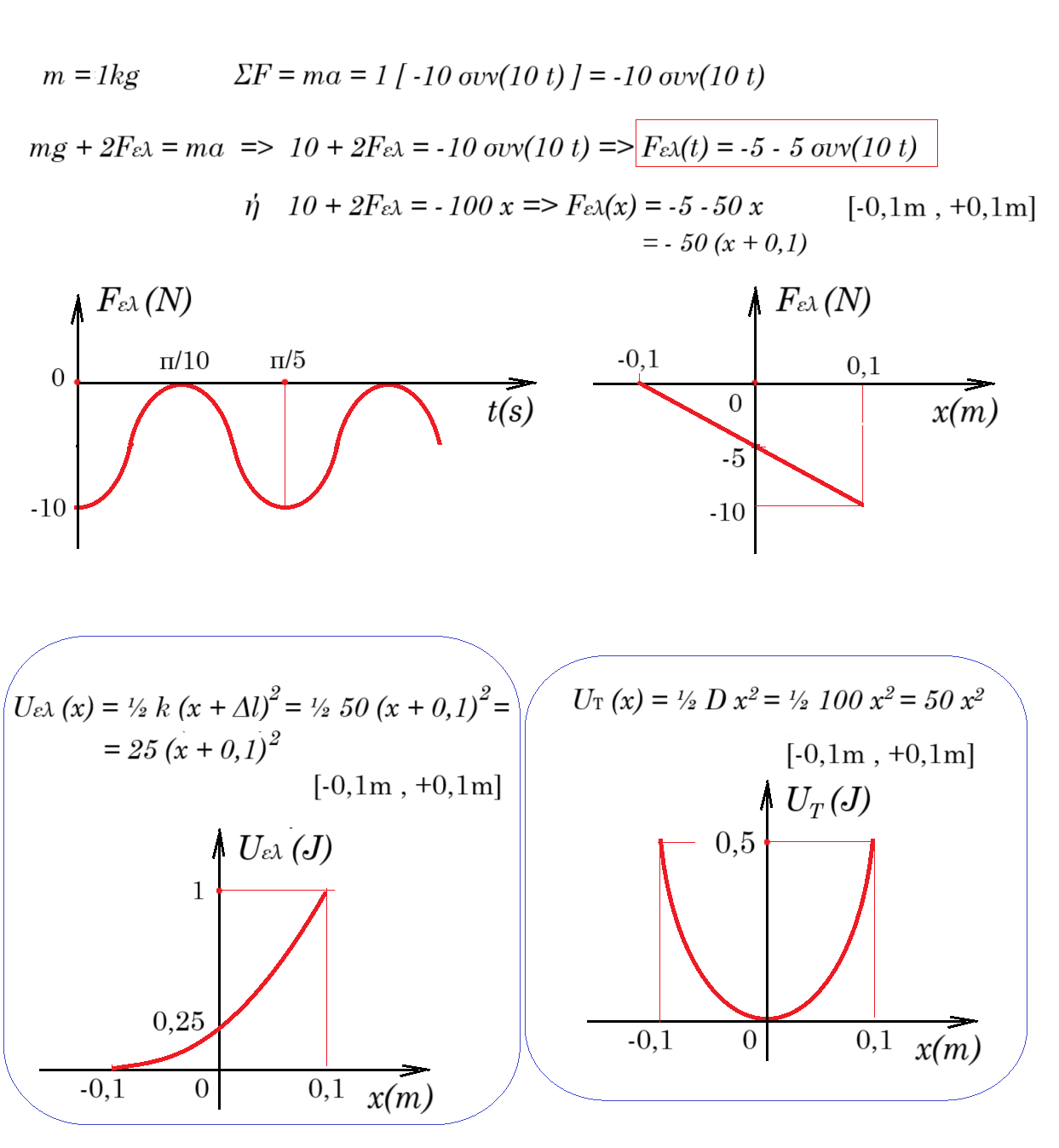
          =>   F_ελ(t) = - 10 - 40 ημ(10.t)    

  στο σώμα Σ₁  ασκείται από το ελατήριο δύναμη  F_ελ(t) = - 10 - 40 ημ(10.t)  

                                                   ή    F_ελ(x) = - 10 - 100.x     [-0,4m , +0,4m]

  στο σώμα Σ₂  ασκείται από το ελατήριο δύναμη  F'_ελ(t) =  10 + 40 ημ(10.t)  

                                                  ή    F'_ελ(x) =  10 + 100.x     [-0,4m , +0,4m]

για το σώμα Σ₂ έχουμε : 

     ΣF = 0   =>  M₂ g  +  F'_ελ(x)  +  N  =  0  =>  N = - 30 - 10 - 40 ημ(10.t) =>

     =>   N(t) = - 40 - 40 ημ(10.t)     ή     N(x) = - 40 - 100.x     [-0,4m , +0,4m]  

U_ελ = 0,5 k (x + Δl)² = 0,5  100  (x + 0,1)²  => U_ελ(x) = 50 (x + 0,1)²   [-0,4m , +0,4m]

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Στο σχήμα, η ράβδος ΑΓ μάζας m = 1 kg ισορροπεί σε οριζόντια θέση. Τα άκρα της Α, Γ συνδέονται στα άκρα των δύο όμοιων ιδανικών ελατηρίων σταθεράς  k = 50 N/m.  Απομακρύνουμε την ράβδο κατακόρυφα προς τα κάτω κατά  χ₀ = 0,1 m  και τη στιγμή t₀ = 0 την αφήνουμε ελεύθερα να κινηθεί.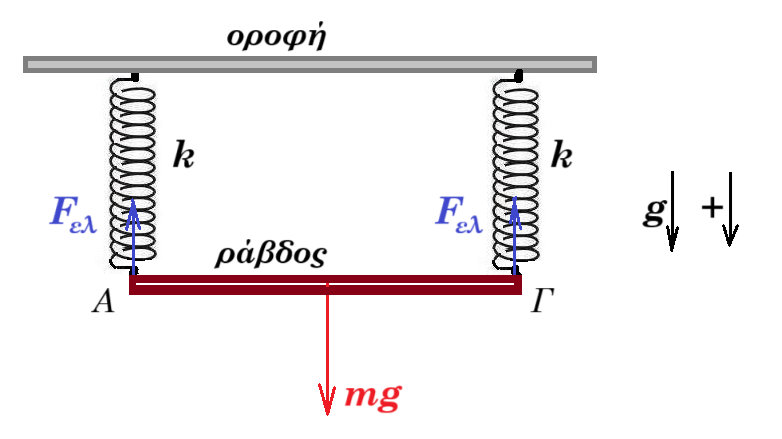  

Α)  Δείξτε ότι η ράβδος θα εκτελέσει Α.Α.Τ ,  βρείτε την συχνότηα της ταλάντωσης της ράβδου.

Β)  Σχεδιάστε σε βαθμολογημένους άξονες την γραφική παράσταση της δυναμικής ενέργειας της ταλάντωσης της ράβδου συναρτήσει της απομάκρυνσής της από τη θέση ισορροπίας της  και  την γραφική παράσταση της δυναμικής ενέργειας του ελατηρίου συναρτήσει της απομάκρυνσης της ράβδου από τη θέση ισορροπίας της.

Γ)  Βρείτε την ενέργεια του συστήματος  ελατηρίων - ράβδου  καθώς η ράβδος κινείται  και  την ενέργεια ταλάντωσης της ράβδου.

Δ)  Βρείτε τον ρυθμό μεταβολής της δυναμικής ενέργειας της ταλάντωσης της ράβδου τη στιγμή που η επιτάχυνση της είναι  + 5 m/s².

  ισορροπία ράβδου :  ΣF = 0 =>  mg - 2 k Δl = 0  =>  Δl = mg / 2k = 10 / 100 =>  Δl = 0,1 m  επιμήκυνση ελατηρίου στη θέση ισορροπίας της ράβδου

όταν αφήσουμε ελεύθερη τη ράβδο, αυτή κινείται προς τα πάνω  και έστω x  μια τυχαία απομάκρυση από τη Θ.Ι. της τ΄τε :  ΣF = mg - 2 k (Δl + x) =  mg - 2 k Δl  -  2 k x =  - 2 k x  =>  ΣF = - 2 k x    

η συνισταμένη δύναμη που ασκείται στη ράβδο είναι ανάλογη της απομάκρυνσης από τη Θ.Ι. της  αυτό σημαίνει ότι η ράβδος θα εκτελέσει Απλή Αρμονική Ταλάντωση  με σταθερά  D = 2k = 2 50 N/m = 100 N/m και κυκλική συχνότητα  ω² = D/m = 100 N/m / 1 kg = 100 =>  ω = 10 rad/s    

το πλάτος της ταλάντωσης είναι  Α = χ₀ = 0,1 m   διότι τι στιγμή  t₀ = 0  η ράβδος έχει μηδενική ταχύτητα  και είναι σε απομάκρυση  χ₀  από τη θέση ισορροπίας της  προς την θετική κατεύθυνση  άρα είναι σε απομάκρυνση  +Α    

η συχνότητα της ταλάντωσης είναι :   f = ω/2π  = 10 / 2π Hz =  5/π Hz  

ο χρόνος περιόδου της ταλάντωσης της ράβδου είναι :  Τ = 1/f = π/5 s      

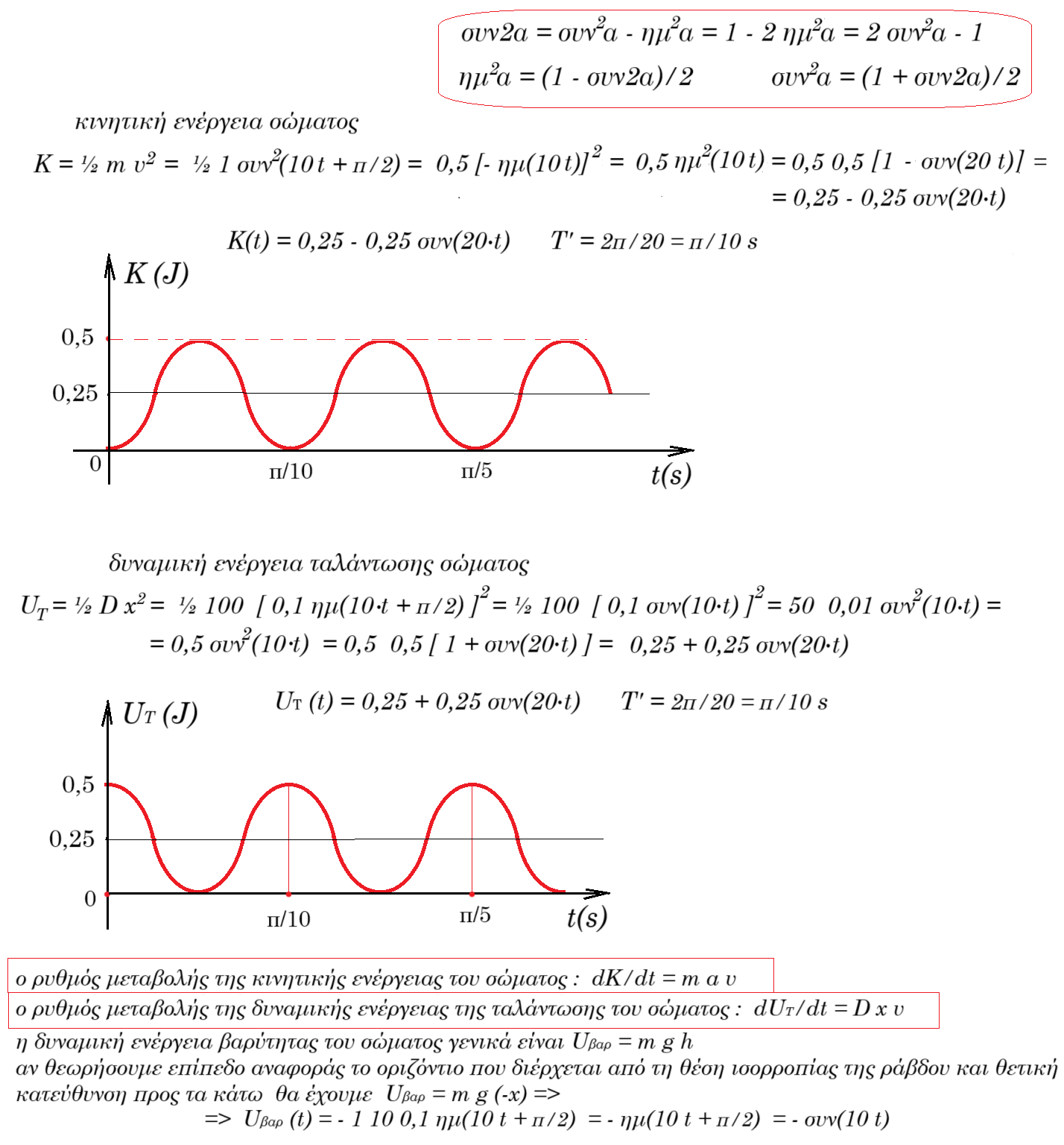
θεωρώ σαν επίπεδο αναφοράς το οριζόντιο επίπεδο που διέρχεται από την κατώτατη θέση ταλαντώσεως της ράβδου    η δυναμική ενέργεια βαρύτητας είναι 

             U_βαρ = m g h =  m g (Α - x) =  1  10  ( 0,1 - x )  = 1  -  10 x  =

                      =  1  -  10  0,1 ημ(10t + π/2)  =  1  -  ημ(10t + π/2) =  1 - συν(10t)

(1)     όταν η ράβδος είναι στην κάτω ακραία θέση  x = + 0,1 m    οπότε  υ = 0    έχει

  δυναμική ενέργεια βαρύτητας  U_βαρ = m g h = 0

  κινητική ενέργεια μηδέν

  τα ελατήρια είναι επιμηκυμένα κατά  0,2 m  οπότε έχουν δυναμική ενέργεια  U  = 0,5 k x²  =  0,5 50 0,2² = 1 J   το κάθε ένα  άρα  τα δύο ελατήρια έχουν ενέργεια  2 J 

 η ενέργεια του συστήματος είναι   U_βαρ  +  K  + U_ελ  =  0  + 0   +  2 J  =  2 J    

(2)     όταν η ράβδος διέρχεται από την θέση ισορροπίας της :  x = 0    οπότε  v = ± 1 m/s   έχει

  δυναμική ενέργεια βαρύτητας  U_βαρ =  m g h  =  1kg 10 m/s²  0,1 m  = 1 J 

  κινητική ενέργεια μέγιστη  Κ = ½ m v² =  ½  1  1 = 0,5 J 

  τα ελατήρια είναι επιμηκυμένα κατά  0,1 m  οπότε έχουν δυναμική ενέργεια  U  = 0,5 k x²  =  0,5 50 0,1² = 0,25 J   το κάθε ένα  άρα  τα δύο ελατήρια έχουν ενέργεια  0,5 J 

 η ενέργεια του συστήματος είναι   U_βαρ  +  K  + U_ελ  =  1 J  +  0,5 J  +  0,5 J   =  2 J    

(3)     όταν η ράβδος είναι στην πάνω ακραία θέση  x = - 0,1 m    οπότε  υ = 0    έχει

  δυναμική ενέργεια βαρύτητας  U_βαρ = m g h = 1kg  10 m/s²   0,2 m =  2 J 

  κινητική ενέργεια μηδέν

  τα ελατήρια έχουν το φυσικό τους μήκος οπότε η δυναμική τους ενέργεια είναι μηδέν

 η ενέργεια του συστήματος είναι   U_βαρ  +  K  + U_ελ  =  2 J  + 0   +  0  =  2 J    

η ενέργεια της ταλάντωσης της ράβδου είναι :  Ε = ½ D A²  =  ½  100  0,1²  =  0,5 J        

       a = + 5 m/s² =>  a = - ω² x =>  5 = - 100 x  =>  x = - 0,05 m  = - A/2  

0,5 D x² + 0,5 m v² = 0,5 D A²  =>  100  0,05²  +  1 v²  =  100  0,1²  =>  0,25  +  v²  =  1  =>  v² = 0,75 = 3/4  =>  v = ± √3/2 m/s 

  dU_T /dt = D x v =  100  (- 0,05)  (± √3/2)  =  ± 5√3/2 J/s

........................................................................................................................................................................................................

.......................................................................................................................................................

...............................................................................................................................................

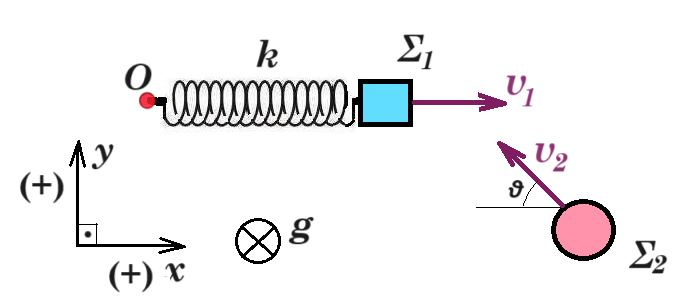
Σφαιρίδιο Σ₁ με μάζα m₁ = 1 kg εκτελεί απλή αρμονική ταλάντωση μηδενικής αρχικής φάσης με σταθερά επαναφοράς D = k και πλάτους Α = 0,2 m πάνω σε λείο οριζόντιο επίπεδο στην διάρκεια της οποίας στον άξονα κίνησης δέχεται μόνο την δύναμη από το ελατήριο. Το σφαιρίδιο είναι δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου φυσικού μήκους ℓ₀ = 0,5 m και σταθεράς k = 100 N/m. Το άλλο άκρο του ελατηρίου Ο είναι αρθρωμένο κατάλληλα ώστε το ελατήριο να μπορεί να περιστρέφεται ως προς κατακόρυφο άξονα χωρίς να έχουμε ανάπτυξη τριβών. Την χρονική στιγμή t₁ = π/60 s το Σ₁ συγκρούεται πλαστικά με σφαιρίδιο Σ₂  μάζας  m₂ = 0,5 kg με αποτέλεσμα το συσσωμάτωμα που δημιουργείται να εκτελεί ομαλή κυκλική κίνηση. Να θεωρήσετε ως θετική φορά της ταλάντωσης που εκτελεί το Σ₁ την φορά που δείχνει μακριά από το άκρο Ο του ελατηρίου.
Να υπολογίσετε :
1) το μέτρο της ταχύτητας του συσσωματώματος.
2) την θερμότητα (Q) που εκλύθηκε στην διάρκεια της κρούσης.

  k = m₁ ω²  =>  100 = 1 ω²  =>  ω = 10 rad/s       T = 2π/ω = 2π/10 = π/5 s          t₁ = π/60 s = Τ/12 

  x = 0,2 ημ(10t)              v = 2 συν(10t)                α = - 20 ημ(10t) 

    x = 0,2 ημ(10 π/60)  =  0,2 ημ(π/6) = 0,1 m    επιμήκυνση ελατηρίου

τη στιγμή της κρούσης  το ελατήριο έχει επιμήκυνση  0,1 m,  επειδή το φυσικό του μήκος είναι  0,5 m  εκείνη τη στιγμή θα έχει μήκος  0,6 m    ενώ  το σώμα Σ₁  κινείται προς τα δεξιά με ταχύτητα  v₁ = 2 συν(10  π/60)  =  2 συν(π/6)  =  + 2 √3/2  =  + √3 m/s    

κατά την κρούση έχουμε διατήρηση της ορμής :  m₁ v₁  -  m₂ v_2x  =  (m₁ + m₂) u_x   (1)         

    m₂ v_2y  =  (m₁ + m₂) u_y    (2)           

επειδή το συσσωμάτωμα θα εκτελέσει  ομαλή κυκλική κίνηση  η συνιστώσα  u_x = 0   οπότε   m₁ v₁  -  m₂ v_2x  =  0   =>  1 kg  √3 m/s  -  0,5 kg  v_2x  =  0  =>  v_2x = 2√3 kg.m/s   

 η δύναμη του ελατηρίου έχει κατεύθυνση προς το σημείο Ο  και  παίζει το ρόλο  της κεντρομόλου δύναμης   ισχύει :  F_ελατ = F_κ  =>  k x₁  =  (m₁ + m₂) u_y² / r  =  (m₁ + m₂) u_y² / (l₀ + x₁)  =>

     =>  (m₁ + m₂) u_y²  =  k x₁ (l₀ + x₁)  =>  1,5  u_y²  =  100  0,1  0,6  =>   u_y²  =  6/1,5  =  4   => 

     =>   u_y = 2 m/s   (3)         u = 2 m/s   

  (2) , (3) =>    m₂ v_2y  =  (m₁ + m₂) u_y   =>  0,5 kg  v_2y  =  1,5 kg  2 m/s   =>  v_2y =  6 m/s    

    v₂² = v_2x² + v_2y² =  ( 2√3 )²  + ( 6 )²  =  12  +  36 =   48  =>  v₂  =  4√3 m/s   

 Q_θερμ  =  0,5 (m₁ + m₂) u²  -  0,5 m₁ v₁²  -  0,5 m₂ v₂²  =  0,5  1,5  4  -   0,5  1  3   -   0,5  0,5  48  =  

       =   3  -   1,5   -   12  =>   Q_θερμ  =  - 10,5 J     

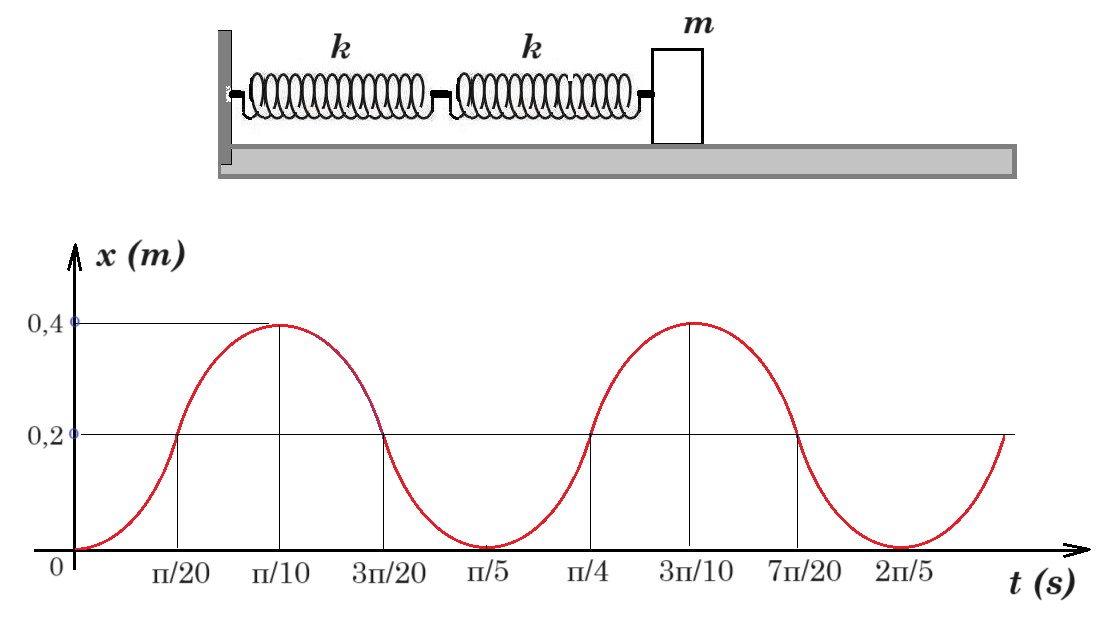
To σώμα αρχικά ηρεμεί. Η μάζα του είναι 2 kg. Ασκούμε σταθερή οριζόντια δύναμη που έχει τη διεύθυνση του άξονα των ελατηρίων, φορά προς τα δεξιά. Το σώμα εκτελεί αρμονική ταλάντωση και η θέση του δίνεται από το διάγραμμα.

α)  Να υπολογισθούν οι σταθερές των ελατηρίων και η δύναμη.

β)  Σε πόσο χρόνο από την στιγμή που δρα η δύναμη θα ακινητοποιηθεί στιγμιαία;
γ)  Ποια είναι η ισχύς της δύναμης που ασκούμε την πρώτη φορά που το σώμα απέχει 0,1 m από τη θέση
ισορροπίας της ταλάντωσής του;

  ΣF = m a  =>  F  -  k/2 x  =  m dv/dt       

    x =  x₁ + x₂ =>  F/D  =  F/k + F/k  =  2F/k  =>  D = k/2       

  T = π/5 s  =>  ω = 2π/Τ  =  2π / (π/5) = 10 rad/s      D = m ω²  =>  k/2  =  2  100   =>  k = 400 N/m       

  θέση ισορροπίας :  F  -  k/2 x₀  =  0  =>  x₀ = 2F/k  =  0,2  =>  2F = 0,2k   =>  F = 0,1 k  =  0,1  400  =  40 N

 ΣF = F  -  k/2 x          x = 0   t = 0    ΣF =  40  -  400/2  0  =  + 40 N   =  m a  =>  a = + 20 m/s²    v = 0  

 x = 0,2 m    t = T/4 = π/20 s    ΣF =  40  -  400/2  0,2  =  0      v = v_max = ωΑ = 10  0,2  = 2 m/s    

 x = 0,4 m    t = T/2 = π/10 s    ΣF =  40  -  400/2  0,4  =  - 40 N    =  m a  =>  a = - 20 m/s²        v = 0  

  x =  0,2  +  0,2 ημ(10t + 3π/2)            v =  2 συν(10t + 3π/2)          α =  - 20 ημ(10t + 3π/2)       

 F  -  k/2 x  =  m dv/dt  =>  F  -  k/2 A ημ(ωt + 3π/2)  =  - mω²A ημ(ωt + 3π/2)  

   P_F  =  F v =  40  2 συν(10t + 3π/2)  =  80 συν(10t + 3π/2)

    x =  0,2  +  0,2 ημ(10t + 3π/2)  =  0,1 m   =>  0,2 ημ(10t + 3π/2)  =  - 0,1  =>  ημ(10t + 3π/2)  =  - 0,5     τότε     συν(10t + 3π/2)  =  +√3/2   οπότε    v =  2  √3/2  =  √3 m/s    

     P_F  =  80 συν(10t + 3π/2)  =  40√3 J/s

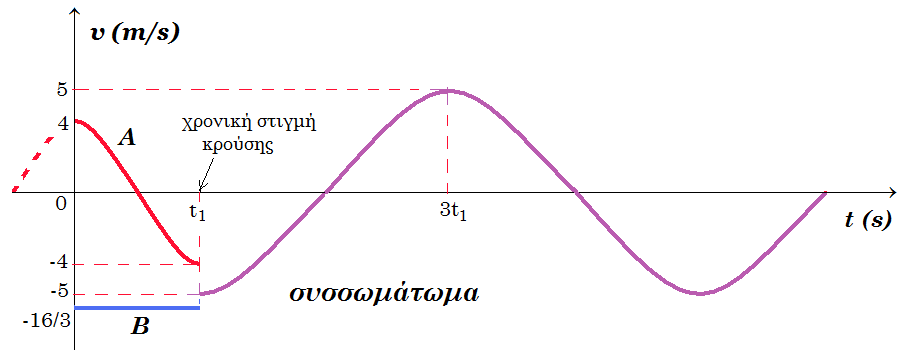
Σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ενός ιδανικού ελατηρίου, ταλαντώνεται ένα σώμα Α μάζας m₁=1kg, ενώ ένα δεύτερο σώμα Β κινείται με σταθερή ταχύτητα πλησιάζοντας προς το Α σώμα, όπως στο σχήμα. Λαμβάνοντας κάποια στιγμή ως αρχή μέτρησης των χρόνων και ορίζοντας την προς τα δεξιά κατεύθυνση ως θετική, χαράξαμε την γραφική παράσταση της απομάκρυνσης του Α σώματος σε συνάρτηση με το χρόνο, παίρνοντας το διάγραμμα του σχήματος, όπου την στιγμή t₁=π/10 s τα δύο σώματα συγκρούσθηκαν κεντρικά. Αντλώντας πληροφορίες από το διάγραμμα, να απαντήσετε στις παρακάτω ερωτήσεις:

(α)  Η κρούση είναι  ελαστική  πλαστική   ή  ανελαστική;  Δικαιολογήστε την άποψή σας.

(β)  Να υπολογιστεί η σταθερά του ιδανικού ελατηρίου, με το οποίο συνδέεται το Α σώμα.

(γ)  Να βρεθεί η ταχύτητα του σώματος Α ελάχιστα πριν την κρούση, καθώς και η κοινή ταχύτητα των σωμάτων ακριβώς μετά την κρούση.

(δ)  Να γίνει η γραφική παράσταση της ταχύτητας των σωμάτων Α και Β σε συνάρτηση με το χρόνο, για t ≥ 0.

 t₁ = T₁/2 => T₁ = 2 π/10 = π/5 s     ω₁ = 2π/T₁ = 10 rad/s       k = m₁ ω₁² = 1 10² =>  k = 100 N/m

   T ' = 4 t₁ = 4 π/10  = 2π/5 s       ω' = 2π/T ' = 5 rad/s       k = M (ω')² =>  100  =  M 5² =>  M = 4 kg  

άρα η κρούση είναι πλαστική  και  το σώμα Β έχει μάζα  m₂ = 3 kg

η κρούση γίνεται τη στιγμή t₁  που το σώμα Α έχει μηδενική απομάκρυνση  δηλαδή διέρχεται από τη θέση ισορροπίας του   άρα έχει μέγιστη ταχύτητα   v₁ = ω₁ Α₁ = 10 rad/s  0,4 m  =>  v₁ = 4 m/s       από  0  έως  t₁  η απομάκρυνση του σώματος Α είναι θετική  (από το διάγραμμα)  το σώμα έχει πάει στο θετικό άκρο της ταλάντωσής του και κινείται προς τα αριστερά  συνεπώς τη στιγμή  t₁  περνά από τη Θ.Ι. του με αρνητική ταχύτητα  άρα   v₁ = - 4 m/s      

μετά την κρούση  το συσσωμάτωμα θα εκτελέσει Α.Α.Τ.  χωρίς να αλλάξει η θέση ισορροπίας  οπότε θα έχει μέγιστη  ταχύτητα   u = ω' Α' = 5 rad/s  1 m =>  u = 5 m/s 

διατήρηση ορμής  πλαστική κρούση :  m₁ v₁  +  m₂ v₂ = (m₁ + m₂) u  =>  - 1  4 + 3 v₂ = - 4  5  =>  v₂ = - 16/3 m/s 

ΘΕΜΑ Γ

Το σώμα (1) μάζας m₁ =1Kg συνδέεται με το πάνω άκρο του ιδανικού κατακόρυφου ελατηρίου (1) σταθερής k₁ =100N/m, το κάτω άκρο του ιδανικού κατακόρυφου ελατηρίου (2) με k₂ =100N/m και είναι ακίνητο. Το πάνω άκρο του ελατηρίου (2) συνδέεται με το ακίνητο σώμα (2) μάζας m₂=2Kg, το οποίο συνδέεται με το κάτω άκρο του αβαρούς, μη ελαστικού, κατακόρυφου νήματος. Το πάνω άκρο του νήματος συνδέεται με το ταβάνι. Το ελατήριο (1) έχει το φυσικό του μήκος και συνδέεται με σώμα (3) μάζας m₃=2Κg το οποίο είναι ακίνητο στο δάπεδο. 
Kατεβάζουμε το σώμα (1) κατά d και τα κρατάμε.  Τη χρονική στιγμή t=0 το αφήνουμε. Θεωρούμε θετική φορά για τις αλγεβρικές τιμές προς τα κάτω και τα σώματα χωρίς διαστάσεις.
Α.   Να βρεθεί η μέγιστη τιμή της απόστασης d για να εκτελεί το σώμα (1) ΑΑΤ και τα σώματα (2), (3) να παραμένουν ακίνητα (5 μονάδες)
Β.   Αν η απόσταση d είναι η μέγιστη του ερωτήματος Α, να βρεθούν
Β1)  Οι εξισώσεις της απομάκρυνσης και της ταχύτητας των σώματος (1) σε συνάρτηση με το χρόνο. (4 μονάδες)
Β2)  Η δύναμη Τ η οποία ασκείται από το νήμα στο σώμα (2) και της κάθετης αντίδρασης Ν στο σώμα (3) από το δάπεδο συναρτήσει της απομάκρυνσης και συναρτήσει του χρόνου. Να γίνουν οι αντίστοιχες γραφικές παραστάσεις. (6 μονάδες)
Β3)  Το ρυθμό μεταβολής της κινητικής ενέργειας του σώματος (1) συναρτήσει του χρόνου και ειδικά όταν διέρχεται από τη θέση του φυσικού μήκους του ελατηρίου (2) με φορά προς τα πάνω. (4 μονάδες)
Β4)  Η απομάκρυνση του σώματος (1) για την οποία η δυναμική ενέργεια του ελατηρίου (1) ισούται με τη δυναμική ενέργεια του ελατηρίου (2).  Nα γίνουν οι γραφικές παραστάσεις των δυναμικών ενεργειών των ελατηρίων συναρτήσει της απομάκρυνσης. (6 μονάδες)

  ισορροπία  (1) :  m₁ g = F_ελατ,2 =  k₂ Δl₂  =>  10 = 100 Δl₂  =>  Δl₂ = 0,1 m    το ελατήριο (2) είναι επιμηκυμένο στη Θ.Ι. 

  ισορροπία  (2) :  m₂ g + F_ελατ,2 =  Τ  =>   m₂ g + m₁ g =  Τ  =>  Τ = 30 Ν     

σώμα (1) : ΣF₍₁₎ = - k₁ x - k₂ (x + Δl₂) + m₁ g = - k₁ x - k₂ x - k₂ Δl₂ + m₁ g  = - (k₁ + k₂) x    

   D = k₁ + k₂ = 200 N/m      ω = √(D/m₁) = 10√2 rad/s       x  =  d ημ(ωt + π/2)    

καθώς το σώμα (1) ταλαντώνεται, όταν μετατοπίζεται από την Θ.Ι. προς τα κάτω,  το ελατήριο (1) συσπειρώνεται οπότε ασκεί δύναμη στο σώμα (3) προς τα κάτω με συνέπεια να αυξάνεται η δύναμη Ν προς τα πάνω που δέχεται το σώμα (3) από το δάπεδο   επίσης   το ελατήριο (2) το οποίο ήδη είναι επιμηκυμένο  επιμηκύνεται περισσότερο οπότε ασκεί δύναμη στο σώμα (2) προς τα κάτω με συνέπεια να αυξάνεται η δύναμη Τ προς τα πάνω που δέχεται το σώμα (2) από το νήμα

όταν το σώμα (1) μετατοπίζεται από την Θ.Ι. προς τα πάνω,  το ελατήριο (1) επιμηκύνεται οπότε ασκεί δύναμη στο σώμα (3) προς τα πάνω με συνέπεια να μειώνεται η δύναμη Ν προς τα πάνω που δέχεται το σώμα (3) από το δάπεδο οπότε για κάποα τιμή της μετατόπισης έχουμε Ν = 0    επίσης   το ελατήριο (2) το οποίο ήδη είναι επιμηκυμένο, μειώνεται η επιμήκυνσή του  ή  συσπειρώνεται  οπότε ασκεί δύναμη στο σώμα (2) προς τα πάνω με συνέπεια να μειώνεται η δύναμη Τ προς τα πάνω που δέχεται το σώμα (2) από το νήμα οπότε για κάποα τιμή της μετατόπισης έχουμε Τ = 0

για το σώμα (1) η δύναμη του ελατηρίου (2) είναι : F_ελατ,2 = - k₂ (x + Δl₂) = - 100 (x + 0,1)  

για το σώμα (2) η δύναμη του ελατηρίου (2) είναι :  - F_ελατ,2 = + 100 x + 10 

ακινησία σώματος (2) :  m₂ g + (- F_ελατ,2 ) + Τ = 0  =>^Τ=0  20 + 100 x + 10 = 0  => x = - 0,3 m   όταν το σώμα (1) μετατοπίζεται προς τα πάνω κατά 0,3 m  από τη Θ.Ι.  η δύναμη T = 0 

για το σώμα (1) η δύναμη του ελατηρίου (1) είναι : F_ελατ,1 = - k₁ x = - 100 x 

για το σώμα (3) η δύναμη του ελατηρίου (1) είναι :  - F_ελατ,1 = + 100 x  

 ακινησία σώματος (3) :  m₃ g +  (- F_ελατ,1 )  +  N  = 0 =>^Ν=0  20  + 100 x = 0 => x = - 0,2 m  όταν το σώμα (1) μετατοπίζεται προς τα πάνω κατά 0,2 m  από τη Θ.Ι.  η δύναμη Ν = 0 το σώμα (3) απλώς ακουμπά στο οριζόντιο δάπεδο

       τότε  x_max = 0,2 m = d  μέγιστο πλάτος ταλάντωσης       ( d = 0,2 m < 0,3 m )

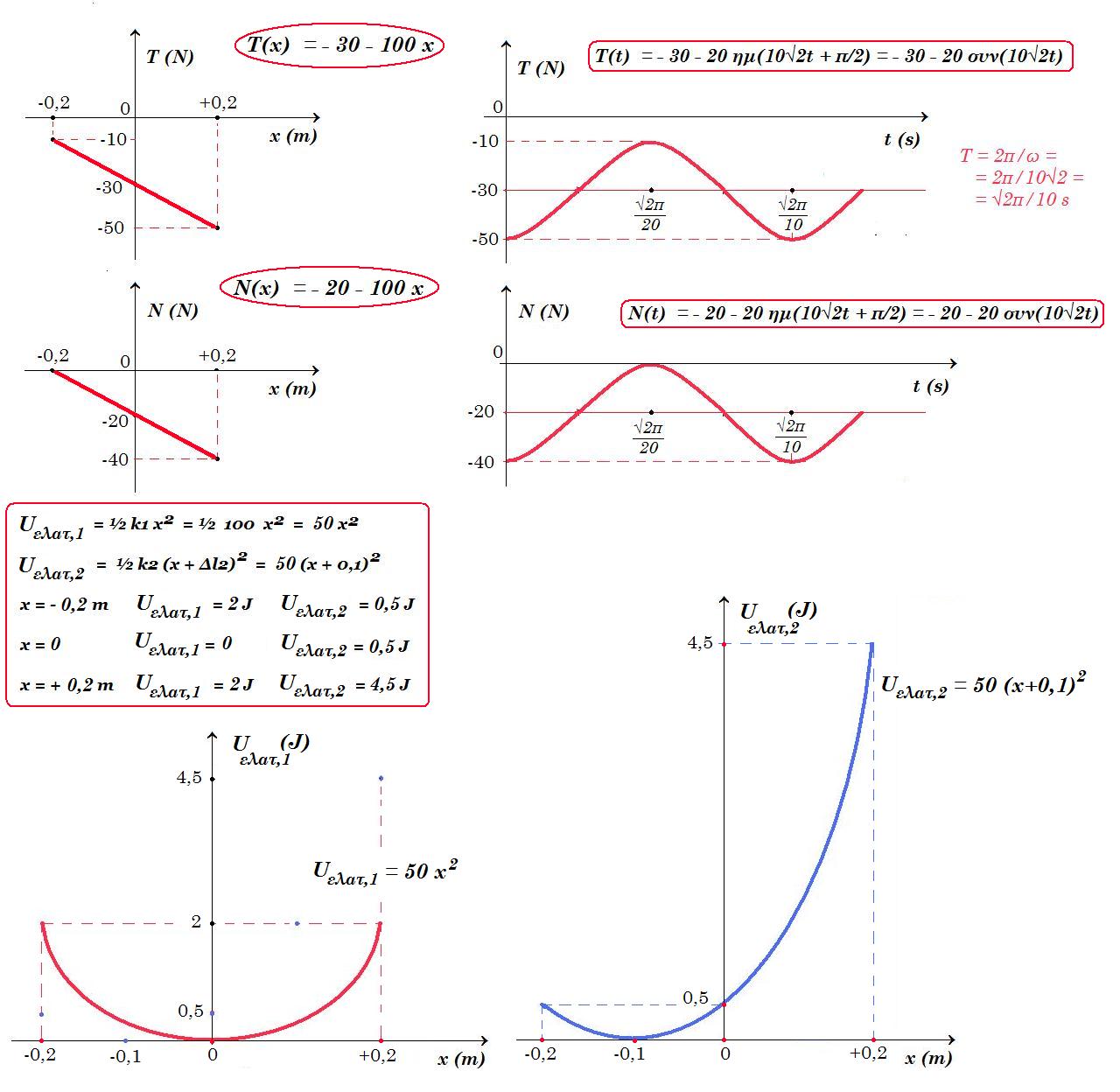
   x(t) = 0,2 ημ(10√2.t + π/2)          v(t) = 2√2 συν(10√2.t + π/2)       α(t) = - 40 ημ(10√2.t + π/2)  

     Τ(x)  = - 30 - 100 x    [- 0,2 m , + 0,2 m]     ή    Τ(t)  = - 30 - 20 ημ(10√2t + π/2)  

     Ν(x)  = - 20 - 100 x   [- 0,2 m , + 0,2 m]     ή     Ν(t)  = - 20 - 20 ημ(10√2t + π/2)

dK/dt  =  m₁ v a  =  1  2√2 συν(10√2.t + π/2)  [ - 40 ημ(10√2.t + π/2) ]  =

         = - 80√2 ημ(10√2.t + π/2) συν(10√2.t + π/2)  =>  dK/dt (t) = - 40√2  ημ(20√2.t + π)   

όταν  x = - 0,1 m = 0,2 ημ(10√2.t + π/2)  =>  ημ(10√2.t + π/2)  = - 0,5      

  συν(10√2.t + π/2) = -√3/2       v < 0       τότε    dK/dt = - 80√2 (- 0,5)  (- √3/2)  = - 20√6 J/s   

U_ελατ,1 = U_ελατ,2  =>  ½ k₁ x² = ½ k₂ (x + Δl₂)²  => x² = (x + 0,1)² =>  x = - x - 0,1 => x = - 0,05 m            

U_ελατ,1  = ½ k₁ x²  = ½  100  x²  =  50 x²                   U_ελατ,2  =  ½ k₂ (x + Δl₂)²  =  50 (x + 0,1)²   

x = - 0,2 m       U_ελατ,1  = 2 J       U_ελατ,2  = 0,5 J

x = 0                U_ελατ,1  = 0         U_ελατ,2  = 0,5 J

x = + 0,2 m      U_ελατ,1  = 2 J      U_ελατ,2  = 4,5 J

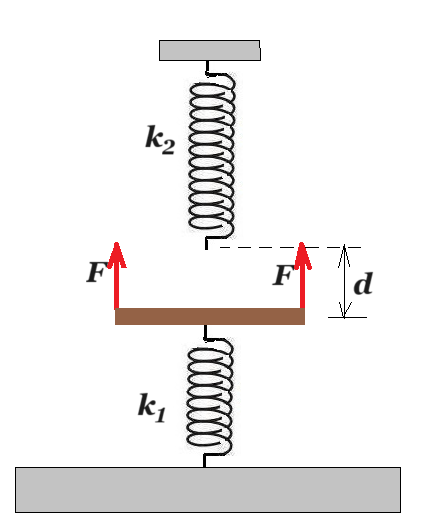Η ομογενής ράβδος είναι ακίνητη, οριζόντια , έχει μάζα m=1Kg  και το μέσο της συνδέεται με το πάνω άκρο του ελατηρίου (1) σταθερής k₁= 100N/m. Το κάτω άκρο του ελατηρίου (1) συνδέεται με το δάπεδο. Το μέσο της ράβδου απέχει κατακόρυφα d=0,1m από το ελεύθερο άκρο του ελατηρίου (2) σταθερής k₂ = 300N/m , του οποίου το άλλο άκρο συνδέεται σε σταθερό σημείο. Τη χρονική στιγμή t=0 ασκούνται στα άκρα της ράβδου ίδιες σταθερές δυνάμεις μέτρου F=5N κατακόρυφα προς τα πάνω.  Να βρείτε:
α)  Τη χρονική στιγμή t₁ που το μέσο της ράβδου ακουμπάει το ελεύθερο άκρο του ελατηρίου (2) , για πρώτη φορά. (t₁ = π/20 s)
β)  Την ταχύτητα της ράβδου τη στιγμή που ακουμπάει το ελεύθερο άκρο του ελατηρίου (2) (u = 1m/s)
γ)  Τη μετατόπιση της ράβδου από τη στιγμή ακουμπάει το ελεύθερο άκρο του ελατηρίου (2) , για
πρώτη φορά μέχρι να μηδενιστεί η ταχύτητά της για πρώτη φορά. (ψ= 0,05m )
δ)  Το πλάτος της ταλάντωσης της ράβδου όταν κατά τη διάρκεια της κίνησής της συνδέεται με το
ελατήριο (1) και είναι σε επαφή με το ελατήριο (2). (Α= 0,05m )
ε)  Το χρονικό διάστημα από τη στιγμή που ασκήθηκαν οι δυνάμεις στη ράβδο , μέχρι να βρεθεί η
ράβδος την επόμενη φορά στην ίδια θέση. ( Δt = 3π/20s )

α)    ισορροπία ράβδου :   m g = k₁ Δl₁  =>  1  10  =  100 Δl₁  =>  Δl₁ = 0,1 m    συσπείρωση 

 ΣF = m a  =>  2F  -  mg  +  F_ελατ =  m a  =>  2F  -  mg  -  k₁ x  =  m α  =>  10  -  10  - 100 x  =  1  α  => 

      =>  - 100 x  =  α   =>  A. A. T.  =>  ω² = 100 =>  ω = 10 rad/s     

    Τ = 2π/ω =  2π/10  = π/5 s       T/4 = π/20 s  =  t₁     

β)   όταν ανέβει η ράβδος κατά  d = 0,1 m  =  Δl₁   το ελατήριο αποκτά το φυσικό του μήκος  οπότε F_ελατ = 0

ΣF = m a  =>  2F  -  mg  +  F_ελατ =  m a  =>  2F  -  mg  -  0  =  m α  =>  10  -  10  =  1  α  =>  α = 0    εκείνη τη στιγμή η ράβδος έχει τη μέγιστη ταχύτητα 

η θέση αυτή είναι η Θέση Ισορροπίας του σώματος για την ταλάντωσή του   άρα το πλάτος ταλάντωσης είναι Α = d = Δl₁ = 0,1 m

   x(t) = 0,1 ημ(10.t + 3π/2)        v(t) = 1 συν(10.t + 3π/2)      α(t) = - 10 ημ(10.t + 3π/2)         v_max = 1 m/s

γ)   όταν ακουμπήσει η ράβδος το επάνω ελατήριο (2)  το  "σπρώχνει" προς τα επάνω  οπότε το ελατήριο (2) συσπειρώνεται  έστω κατά x  ενώ το ελατήριο (1) επιμηκύνεται κατά x,  η κινητική ενέργεια του σώματος  και  το έργο των δύο δυνάμεων F  μετατρέπεται σε δυναμική ενέργεια των δύο ελατηρίων  και  δυναμική βαρυτική ενέργεια του σώματος 

  2F x  +   ½ m v_max²  =   ½ k₁ x²  +  ½ k₂ x²  +  mg x  =>   4F x  +  m v_max²  =   k₁ x²  +   k₂ x²  +  2mg x  =>

  =>  20 x  +  1  1²  =   100 x²  +   300 x²  +  20 x  =>   400 x²  -  1  =  0   =>  x = 1/20 m = 0,05 m        

δ)    το σώμα όταν  συνδέεται με το ελατήριο (1)  εκτελεί  Α.Α.Τ.  με πλάτος  Α = 0,1 m  και  κυκλική συχνότητα  ω = 10 rad/s           ενώ το σώμα όταν  συνδέεται με το ελατήριο (1)   και  είναι σε επαφή με το ελατήριο (2)  εκτελεί  Α.Α.Τ.  με πλάτος  0,05 m   και  κυκλική συχνότητα  ω' = 20 rad/s    ( βλέπε (ε) )    

ε)    το σώμα όταν  συνδέεται με το ελατήριο (1)  και  είναι σε επαφή με το ελατήριο (2)  εκτελεί  Α.Α.Τ.  στην τυχαία απομάκρυνση  x  έχουμε : 

 ΣF = m a  =>  2F  -  mg  +  F_ελατ,1  +  F_ελατ,2  =  m a  =>  2F  -  mg  -  k₁ x  -  k₂ x  =  m α  => 

   =>   10  -  10  - 400 x  =  1  α  =>   - 400 x  =  α   =>  A. A. T.  =>  (ω')² = 400 =>  ω' = 20 rad/s     

    Τ' = 2π/ω' =  2π/20  = π/10 s       T' / 2 = π/20 s       

συνολικό χρονικό διάστημα :   Τ/4  +  Τ'/2  +  Τ/4  =   π/20  +  π/20  +  π/20  =  3π/20 s           

Στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου  σταθεράς  k =100 Ν/m  το άλλο άκρο του οποίου είναι στερεωμένο σε ακλόνητο σημείο  ισορροπεί σώμα μάζας  m = 1 kg.  Το σώμα απομακρύνεται κατακόρυφα προς τα κάτω κατά  d = 5 cm  από τη θέση ισορροπίας του  και τη χρονική στιγμή μηδέν  αφήνεται ελεύθερο να κινηθεί.  Υπολογίστε : 

α) εκφράστε την απομάκρυνση  x,  την ταχύτητα  υ,  την επιτάχυνση  α  συναρτήσει του χρόνου 

β) πόση ταχύτητα έχει το σώμα αν η απομάκρυνση από τη θέση ισορροπίας είναι  x = + 0,03 m ;

γ)  εκφράστε την δύναμη επαναφοράς της ταλάντωσης του σώματος,   την δύναμη του ελατηρίου που ασκείται στο σώμα  συναρτήσει του χρόνου

δ)  εκφράστε την δυναμική ενέργεια της ταλάντωσης του σώματος,  την κινητική ενέργεια του σώματος, την δυναμική ενέργεια του ελατηρίου  συναρτήσει του χρόνου

ε)  εκφράστε τον ρυθμό μεταβολής της κινητικής ενέργειας του σώματος συναρτήσει του χρόνου

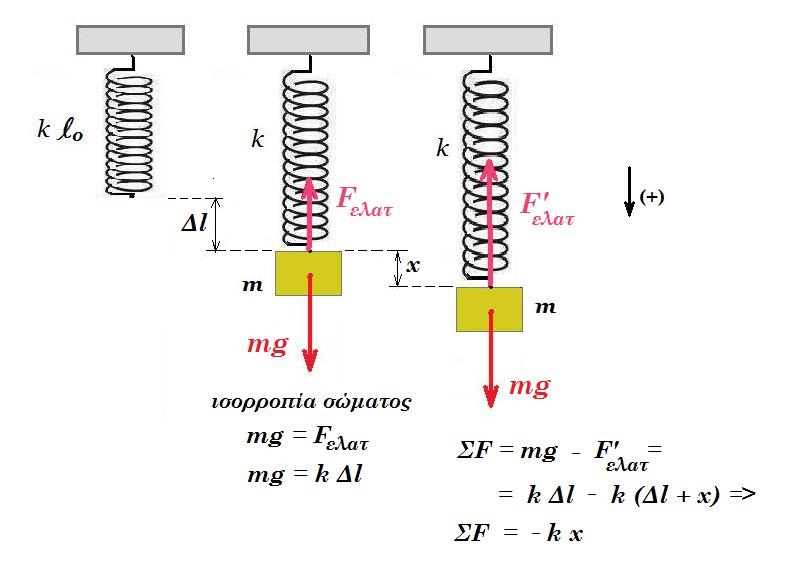
A)  k = m ω²  =>  100 Ν/m  =  1 kg  ω²  =>  ω = 10 rad/s  

      T = 2π/ω = 2π/10 = π/5 sec          f = 1/T  = 5/π Hz 

  ισορροπία σώματος :  ΣF = 0  =>   mg - F_ελατ = 0  =>

                   =>  mg - k Δl = 0  => Δl = mg / k = 10/100 => Δl = 0,1 m

θετική φορά κατακόρυφα προς τα κάτω, πλάτος ταλάντωσης Α = d = 5 cm, αρχική φάση φ = π/2 rad

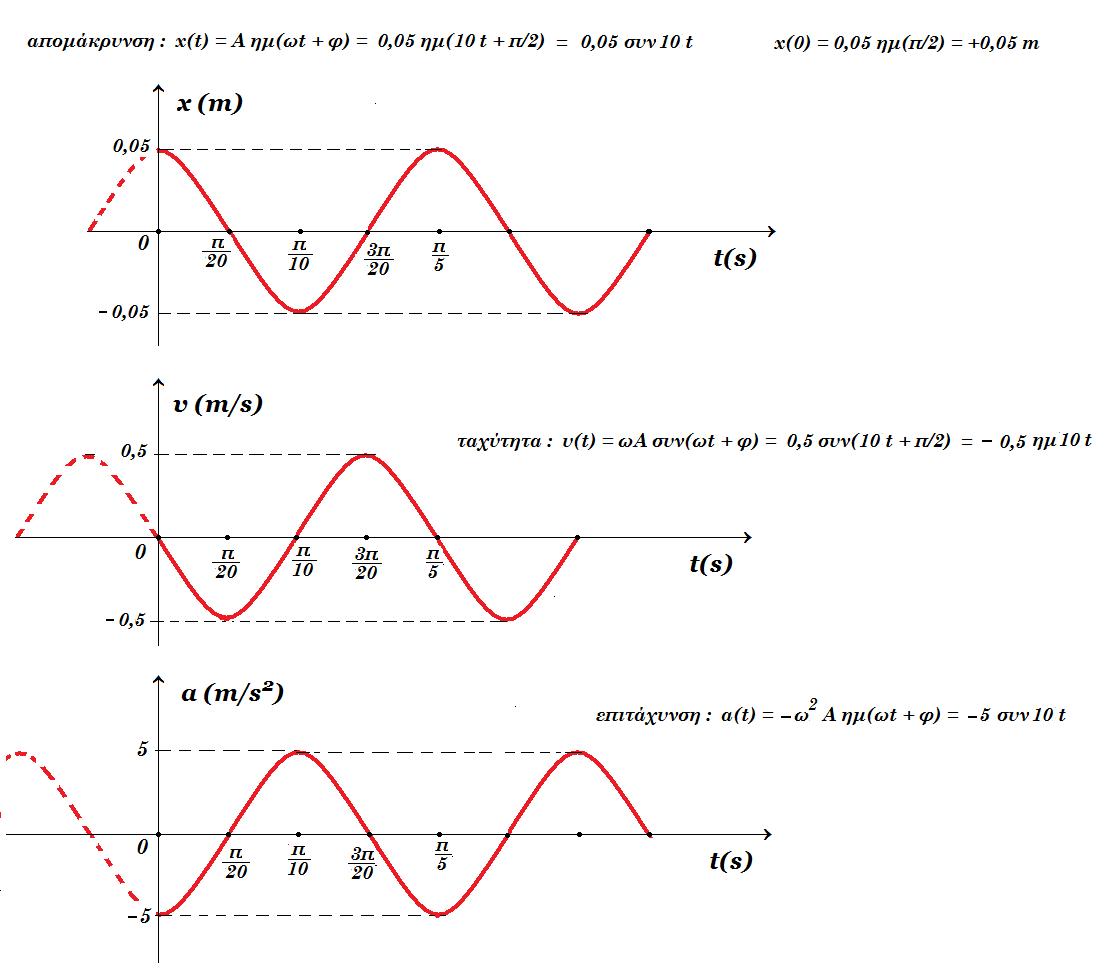
απομάκρυνση :  x(t) = 0,05 ημ(10t + π/2) = 0,05 συν10t      x(0) = 0,05 ημ(π/2) = +0,05 m

ταχύτητα :  υ(t) =  0,5 συν(10t + π/2) = - 0,5 ημ10t

επιτάχυνση :  α(t) = - 5 ημ(10t + π/2) = - 5 συν10t

B)      x =  0,05 ημ(10t + π/2) = 0,03  =>  ημ(10t + π/2)  = 3/5 = 0,6  

    συν(10t + π/2) =  ± 0,8       υ =  0,5 συν(10t + π/2) =  0,5  (± 0,8)  = ± 0,4 m/s  

Γ)  ΣF = m α(t) = - 5 ημ(10t + π/2)     δύναμη επαναφοράς της ταλάντωσης του σώματος

     ΣF = m α(t) =>  F_ελατ + mg  = m α(t)  => F_ελατ + 10  = - 5 ημ(10t + π/2)   =>

      => F_ελατ(t) =  - 10 - 5 ημ(10t + π/2)            F_ελατ(0) = - 10 - 5 ημ(π/2) = - 15 N

F_ελατ(x) = - k (x + Δl) = - 100 (x + 0,1) = - 10 - 100.x        - 0,05 m £ x £ + 0,05 m 

Δ)   U = ½ k x²  =  ½  100  0,05² ημ²(10t + π/2)  =>  U(t) = 0,125 ημ²(10t + π/2)  

      K = ½ m υ²  =  ½  1  0,5² συν²(10t + π/2)  =>  Κ(t) = 0,125 συν²(10t + π/2)  

      U_ελατ = ½ k  (Δl + x)²  =  ½ 100  { 0,1 + 0,05 ημ(10t + π/2) }²  =>

                                           =>  U_ελατ(t)  =  50 { 0,1 + 0,05 ημ(10t + π/2) }²     

U_ελατ = ½ k  (Δl + x)² =  ½ 100  (0,1 + x)²  = 50 (0,1 + x)²     - 0,05 m £ x £ + 0,05 m 

U_βαρυτ(t) = m g (A - x) = 1 10 [ 0,05 - 0,05 ημ(10t + π/2) ] = 0,5 - 0,5 ημ(10t + π/2)     βαρυτική ενέργεια σώματος     

Ε)   ρυθμός μεταβολής κινητικής ενέργειας :

 dK/dt = m υ a = 1 ( - 0,5 ημ10t ) ( - 5 συν10t ) = + 2,5 ημ10t συν10t = + 1,25 ημ20t 

ρυθμός μεταβολής δυναμικής ενέργειας ταλάντωσης :

 dU/dt = k x υ = 100  0,05 συν10t  ( - 0,5 ημ10t ) = - 2,5 ημ10t συν10t = - 1,25 ημ20t 

   κάτω ακραία θέση 

U(0)  =  0,125 ημ²(π/2)  =  0,125 J               Κ(0)  =  0,125 συν²(π/2)  = 0  

U_ελατ(0) = 50 { 0,1 + 0,05 ημ(π/2) }² = 50 { 0,1 + 0,05 }² = 50  0,15² = 1,125 J    

U_βαρυτ(0)  =  0,5 - 0,5 ημ(π/2)  =  0   

στην κάτω ακραία θέση το σώμα έχει κινητική ενέργεια και βαρυτική ενέργεια μηδέν  στο ελατήριο έχει αποθηκευθεί ενέργεια  1,125 J

   θέση ισορροπίας

U(T/4)  =  0,125 ημ²(π)  =  0               Κ(T/4)  =  0,125 συν²(π)  = 0,125 J  

U_ελατ(T/4) = 50 { 0,1 + 0,05 ημ(π) }²  =  50  0,1²  = 0,5 J          U_βαρυτ(T/4) = 0,5 - 0,5 ημ(π)  = 0,5 J 

στην θέση ισορροπίας το σώμα έχει κινητική ενέργεια 0,125 J   και βαρυτική ενέργεια 0,5 J  στο ελατήριο έχει αποθηκευθεί ενέργεια 0,5 J  η συνολική ενέργεια είναι 1,125 J  

   άνω ακραία θέση 

U(T/2) = 0,125 ημ²(3π/2) = 0,125 J               Κ(T/2) = 0,125 συν²(3π/2) = 0  

U_ελατ(T/2) = 50 { 0,1 + 0,05 ημ(3π/2) }² = 50 { 0,1 - 0,05 }² = 50  0,05² = 0,125 J 

U_βαρυτ(T/2) =  0,5 - 0,5 ημ(3π/2) = 1 J   

στην άνω ακραία θέση το σώμα έχει κινητική ενέργεια μηδέν  και βαρυτική ενέργεια 1 J   στο ελατήριο έχει αποθηκευθεί ενέργεια  0,125 J     η συνολική ενέργεια είναι 1,125 J  

Το σώμα μάζας m = 10 kg ισορροπεί ακίνητο πάνω σε λείο οριζόντιο δάπεδο δεμένο στο ένα άκρο ιδανικού οριζοντίου ελατηρίου σταθεράς k = 250 N/m. Το άλλο άκρο του ελατηρίου είναι ακλόνητο. Ασκούμε στο σώμα δύναμη κατά τη διεύθυνση του άξονα του ελατηρίου έτσι ώστε το ελατήριο να επιμηκύνεται το μέτρο της δύναμης μεταβάλλεται με την επιμήκυνση του ελατηρίου σύμφωνα με τη σχέση F = 75 + 250x (SI). Η δύναμη F καταργείται όταν η επιμήκυνση του ελατηρίου γίνει x = 0,2 m. Ο λόγος υ_max/υ′_max όπου υ_max η μέγιστη ταχύτητα του σώματος όταν ασκείται η δύναμη και υ′_max η μέγιστη ταχύτητα του σώματος αφού καταργηθεί η δύναμη  είναι:

α. (√3)/2                               β. 1/2                                 γ. 1

    F = 75 + 250 x           F = 0   =>  x = - 75 / 250 = - 0,3 m             F_ελατ = - k x = - 250 N/m  (- 0,3 m) = 75 N  

  F  +  F_ελατ =  75 + 250 x -  250 x  =  75 N