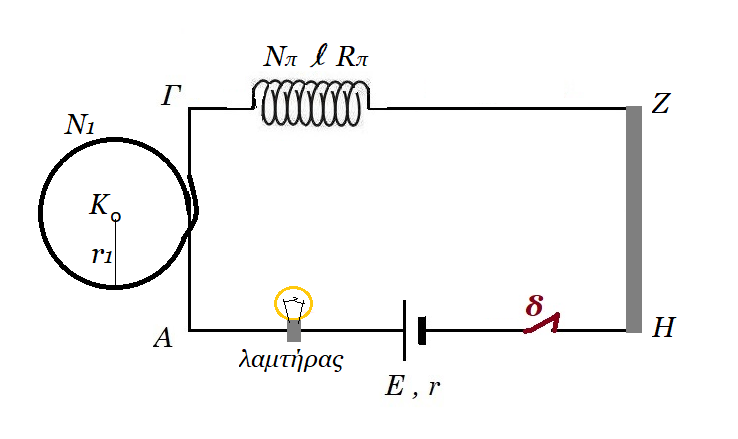
Στο κύκλωμα του σχήματος ο λαμπτήρας έχει ενδείξεις κανονικής λειτουργίας «20W, 10V», ο κυκλικός αγωγός έχει 𝛮1 = 10 σπείρες, ακτίνα 𝑟1 = 10𝑐𝑚 και αντίσταση 𝑅1 = 2𝛺,  το σύρμα  του πηνίου ειδικής αντίστασης  ρ = 2,5 10-9 Ωm  έχει μήκος L = 20π m  και διάμετρο διατομής δ = 0,2 mm  κάθε σπείρα έχει ακτίνα  α = 1𝑐𝑚,   ο ευθύγραμμος αγωγός ΖΗ έχει αντίσταση 𝑅ZH = 2𝛺 και η ηλεκτρική πηγή έχει ΗΕΔ 𝛦 = 30𝑉 και εσωτερική αντίσταση 𝑟.
Η αντίσταση των υπόλοιπων καλωδίων είναι αμελητέα. Το ρεύμα που διαρρέει το κύκλωμα έχει
σταθερή ένταση και ο λαμπτήρας λειτουργεί κανονικά.

 

  Rπ = ρ L /  S =  ρ L /  πδ2/4  =  4ρL / πδ2 =  ( 4 2,5 10-9 Ωm  20π m ) /  ( π 4 10-8 m2 )  =  5 Ω  ωμική αντίσταση πηνίου 

μήκος σύρματος :  L =  Nπ  2π α  =>  20π m  =  Νπ 2π 10-2 m  =>  Νπ  =  1000 σπείρες πηνίου   

μήκος πηνίου :  l = Nπ  δ  = 1000  0,2 mm  =  20 cm =  0,2 m     κάθε σπείρα είναι σε επαφή με την διπλανή της

 

 

 

Στο σχήμα βλέπουμε ένα λείο οριζόντιο επίπεδο και στην περιοχή μεταξύ των ευθειών ΓΗ και ΔΖ επικρατούν δύο κατακόρυφα ομογενή μαγνητικά πεδία, τα οποία διαχωρίζονται από το ευθύγραμμο τμήμα ΚΛ. Τα μέτρα των εντάσεων των πεδίων είναι Β1 και Β2 = 2Β1. Θετικά φορτισμένο σωματίδιο μάζας m και φορτίου q εισέρχεται τη στιγμή t = 0 στο πεδίο έντασης  από το σημείο Α και κάθετα στην πλευρά ΚΛ με ταχύτητα μέτρου υ = (αqB1) / (4m) , όπου  (ΑΛ) = 7α / 8. Να βρεθούν:

Α. το σημείο εξόδου του σωματιδίου από τα πεδία

Β. η στιγμή εξόδου του σωματιδίου από τα πεδία

Γ. το μέτρο της μεταβολής της ορμής του σωματιδίου από τη στιγμή t = 0 μέχρι την έξοδό του από τα πεδία.

 

 

  R2 = mv / qB2   = m ( aqB1 / 4m ) / qB2  =   aB1 / 4 2B1  =>  R2 = a/8     

  Δt1 = T2 / 2 = πm / qB2  = πm / q 2B1  = πm / 2qB1  

  R1 = mv / qB1   = m ( aqB1 / 4m ) / qB1  =   aB1 / 4B1  =>  R1 = a/4     

  Δt2 = T1 / 2 = πm / qB1            Δt3 = T2 / 4 = 2πm / 4qB2  = πm / 2q 2B1  = πm / 4qB1    

    Δtολικό =   Δt1 +  Δt2 +  Δt3 =  πm / 2qB1  + πm / qB1  + πm / 4qB1  = 7πm / 4qB1     

 pαρχική = pτελική = mv = m ( aqB1 / 4m ) =  aqB1 / 4              Δp =  Φ2 pαρχική        

 

  R1 = mv / qB1   = m ( aqB1 / 4m ) / qB1  =   aB1 / 4B1  =>  R1 = a/4     

  R2 = mv / qB2   = m ( aqB1 / 4m ) / qB2  =   aB1 / 4 2B1  =>  R2 = a/8     

  Δt1 = T1 / 2 = πm / qB1           Δt2 = T2 / 2 = πm / qB2  = πm / q 2B1  = πm / 2qB1  

  Δt3 = T1  (φ / 360°) = (2πm / qB1) (60°/360°) = ( 2πm / qB1 )  1/6 = πm / 3qB1    

  Δtολικό =   Δt1 +  Δt2 +  Δt3 =  πm / qB1  + πm / 2qB1  + πm / 3qB1  = 11πm / 6qB1     

   Δp = pαρχική = pτελική = mv = m ( aqB1 / 4m ) =  aqB1 / 4          

 

 

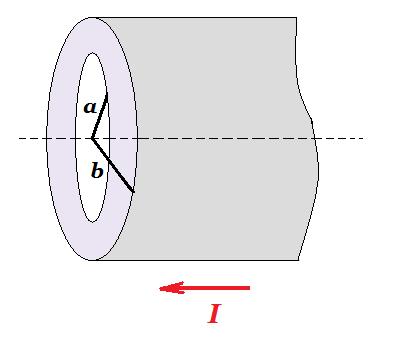
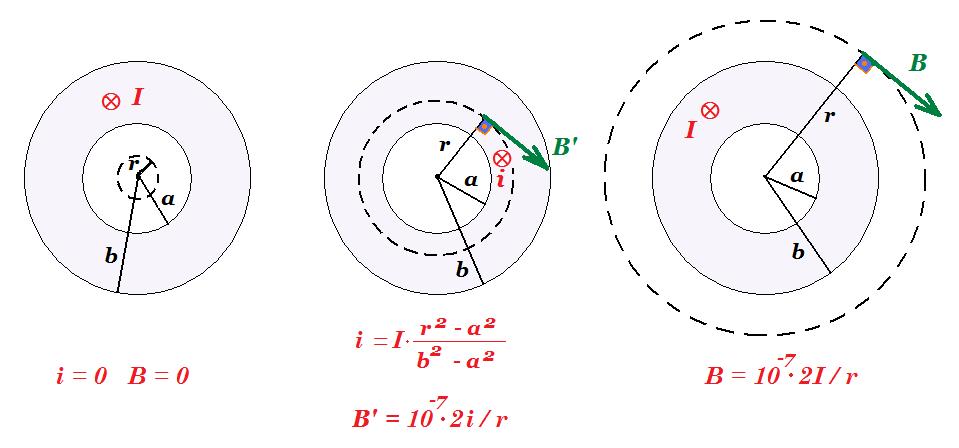
Ένας κοίλος μεταλλικός κύλινδρος έχει εσωτερική ακτίνα a=0,1m και εξωτερική b=0,2m. Ο κύλινδρος διαρρέεται από ρεύμα έντασης Ι =2A το οποίο είναι ομοιόμορφα κατανεμημένο στον αγωγό.
α.  Να υπολογίσετε την ένταση του μαγνητικού πεδίου σε απόσταση 8cm από τον άξονά του.
β.  Να υπολογίσετε την ένταση του μαγνητικού πεδίου σε απόσταση 16cm από τον άξονά του.
γ.  Να βρείτε την απόσταση r, με r > b, από τον άξονα, στην οποία το μαγνητικό πεδίο έχει το ίδιο μέτρο με αυτό που βρήκατε στο ερώτημα β.

α.  8 cm < 0,1 m    ®   i = 0     ®     B = 0  

β.   a = 10 cm  <  r = 16 cm  <  b = 20 cm      i  =  I  π(r2 - a2) / π(b2 - a2)  =>  i  =  2 (162 - 102) / (202 - 102)  =

                                                                             = 2  (256 - 100) / (400 - 100)  =  2  156 / 300  =>  i  =  1,04 A  

  B  =  10-7  2 i / r  =  10-7 N/A2  2  1,04A / 0,16m  =>  B  =  13 10-7 T     

γ.  B  =  10-7  2 i / r  =>  r  = 10-7  2 i /B  = 10-7 N/A2   2  2 A / 13 10-7 T  =>  r =  4/13 m 


...................................................................................................................................................................

ΘΕΜΑ

Θεωρούμε ένα ομοαξονικό σύστημα δύο αγωγών που μεταξύ τους υπάρχει μονωτικό υλικό με μαγνητική διαπερατότητα μ=1 (ομοαξονικό καλώδιο). Ο εσωτερικός αγωγός είναι ένας συμπαγής κύλινδρος με διατομή ακτίνας a=5mm. Ο εξωτερικός αγωγός είναι ένα κυλινδρικό κέλυφος αμελητέου πάχους με διατομή ακτίνας b=10mm. Οι δύο αγωγοί διαρρέονται από σταθερά ρεύματα αντίθετης φοράς που έχουν εντάσεις Ι1 =0,2A και Ι2=0,1A και το ρεύμα στον εσωτερικό αγωγό είναι ομοιόμορφα κατανεμημένο.
Α.  Να υπολογισθεί η ένταση του μαγνητικού πεδίου σε απόσταση
  i. r=3mm από τον κοινό άξονα.
  ii. r=8mm από τον κοινό άξονα.
  iii. r=20mm από τον κοινό άξονα.
B.  Μεταβάλλουμε την ένταση του ρεύματος στον εξωτερικό αγωγό σε Ι2=0,2Α. Να υπολογισθεί η ένταση του μαγνητικού πεδίου σε απόσταση r=12mm από τον κοινό άξονα.

 

(A)   r = 3 mm  <  a = 5 mm       i  =  I1 πr2  / πa2  =  0,2  32 / 52 A  =>  i = 0,072 A          

                                                                          B  =  10-7  2 i / r  = 10-7  2  0,072 / 0,003  =  48 10-7 T  

    a = 5 mm  <  r = 8 mm  <  b = 10 mm          B  =  10-7  2 I1 / r  = 10-7  2  0,2 / 0,008  = 0,5 10-5 T  

        r = 20 mm  >  b = 10 mm             B  =  10-7  2 (I1 - I2) / r  = 10-7  2  (0,2 - 0,1) / 0,02  =  10-6 T  

(B)       r = 12 mm  >  b = 10 mm             B  =  10-7  2 (I1 - I2) / r  = 10-7  2  (0,2 - 0,2) / 0,012  =  0   

 

 

 

ΘΕΜΑ Γ

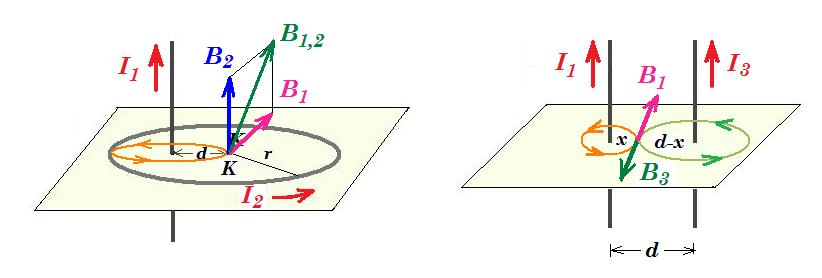
  Β1 = 10-7  2 Ι1 / d  = 10-7  2 3 / (2 10-2) =  3 10-5 Tesla  

  Β2 = 10-7  2π Ι2 / r  = 10-7  2π  (8/π)  / (4 10-2) =  4 10-5 Tesla  

τα διανύσματα  Β1  και  Β2  είναι κάθετα μεταξύ τους  συνεπώς  από πυθαγόρειο θεώρημα :  Β1,2 =  5 10-5 Tesla  

τα διανύσματα  Β1  και  Β3  είναι  αντίθετα  Β1 = Β3  =>    10-7  2 Ι1 / x  = 10-7  2 Ι3 / (d - x)  =>   Ι1 / x  = 3 Ι1 / (d - x)  =>   d - x = 3x  =>   d = 4x  =>  x = 0,02 / 4 m  =  0,005 m

 

..............................................................................................................................................

 

 

 

ΘΕΜΑ 2

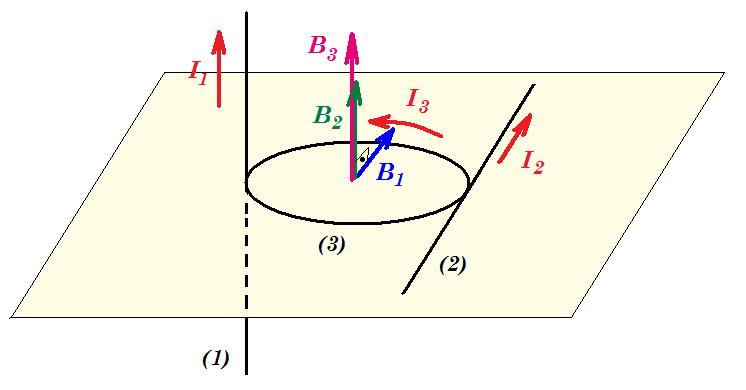
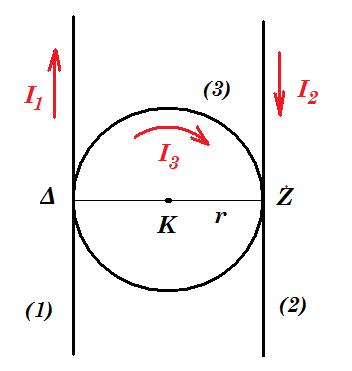
Ένας ηλεκτρικά μονωμένος κυκλικός αγωγός (3) ακτίνας r διαρρέεται από ρεύμα έντασης  Ι3 = 3/π Α  και εφάπτεται στα αντιδιαμετρικά μεταξύ τους σημεία Δ και Ζ με δύο ηλεκτρικά μονωμένους ευθύγραμμους αγωγούς μεγάλου μήκους. Οι τρεις αγωγοί βρίσκονται στο ίδιο επίπεδο, όπως φαίνεται στο διπλανό σχήμα. Οι δύο ευθύγραμμοι αγωγοί διαρρέονται από ίσα ρεύματα, Ι1 = Ι2 = 2Α, αρχικά ίδιας φοράς και το συνολικό μαγνητικό πεδίο στο κέντρο Κ του κυκλικού αγωγού έχει ένταση μέτρου Β = 3∙10–5 Τ.
α) Να υπολογίσετε την απόσταση μεταξύ των δύο ευθύγραμμων αγωγών.
β) Περιστρέφουμε το επίπεδο των αγωγών  (2)  και  (3)  δεξιόστροφα ως προς τον άξονα που συμπίπτει με την ευθεία ΔΖ κατά 90ο , ώστε να γίνει κάθετο στον αγωγό  (1)   χωρίς να αλλάξουμε κάποιο ρεύμα (η κατεύθυνση του ρεύματος έντασης Ι2 γίνεται από τα μάτια του αναγνώστη προς τη σελίδα). Να υπολογίσετε το μέτρο της έντασης του μαγνητικού πεδίου στο κέντρο Κ.
γ) Περιστρέφουμε τους αγωγούς (2) και (3) ακόμη 90ο , ώστε να επανέλθει στο αρχικό επίπεδο τότε η φορά των ρευμάτων θα γίνει αντίθετη από την αρχική. Να υπολογίσετε εκ νέου την ένταση του μαγνητικού πεδίου, στο κέντρο Κ του κυκλικού αγωγού.

 

 

 

 

 

 

 

 

 

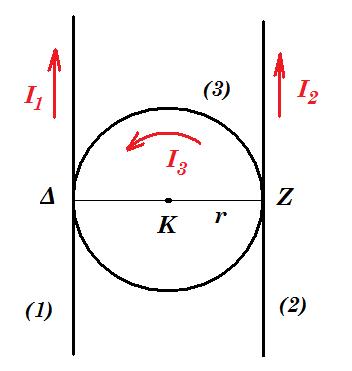
ΘΕΜΑ 2

(α)    B1  =  10-7  2 I1 / r       B2  =  10-7  2 I2 / r           B3  =  10-7  2π I3 / r  

   Βολικό  =  - Β1  +  Β2  +  Β3  =>    3 10-5  =  - 10-7  2 I1 / r   +  10-7  2 I2 / r   +   10-7  2π I3 / r   =>  

        =>  3  =  - 10-2  2 2 / r   +  10-2  2 2 / r   +  10-2  2π 3/π / r   =>   3  =  10-2  ( - 4 + 4 + 6 ) / r   =>  r  =  0,02 m

 

(β)    B1  =  10-7  2 I1 / r  =   10-7  2 2 / 0,02  =  2 10-5 T    

         B2  =  10-7  2 I2 / r  =   10-7  2 2 / 0,02  =  2 10-5 T  

         B3  =  10-7  2π I3 / r  =  10-7  2π  3/π  / 0,02  = 3 10-5 T

   Β'ολικό2  =   Β12  + ( Β2  +  Β3 )2   =  ( 2 10-5 )2   +  ( 2 10-5  + 3 10-5 )2   =  29 10-10    =>  Β'ολικό  =  29½ 10-5 Τ  

  η Β'ολικό  σχηματίζει γωνία  θ  με το επίπεδο των αγωγών (2) και (3)    εφθ  =  Β2,3 / Β1  =  5/2  

 

(γ)   Β"ολικό  =   Β1  +  Β2  +  Β3   = 2 10-5  +   2 10-5   +   3 10-5   =  7 10-5 T  κάθετα στο επίπεδο των αγωγών με φορά προς τα μέσα