Α. Σώμα εκτελεί φθίνουσα ταλάντωση στην οποία η δύναμη απόσβεσης είναι της μορφής F΄= - bυ. Τη χρονική στιγμή t=0 το πλάτος της ταλάντωσης είναι Α0 =10 cm. Το σώμα μέχρι τη χρονική στιγμή t=10 s εκτελεί πέντε πλήρεις ταλαντώσεις, ενώ το πλάτος του μειώνεται κατά 50%.
Να υπολογίσετε:
A1) τη σταθερά Λ της φθίνουσας ταλάντωσης, τη συχνότητα και το πλάτος ταλάντωσης μετά από 15 πλήρεις ταλαντώσεις Μονάδες 10
Α2) τη χρονική στιγμή κατά την οποία το πλάτος θα γίνει Α= 2,5 cm Μονάδες 5
Α3) το έργο της δύναμης απόσβεσης από τη χρονική στιγμή t=0s μέχρι τη χρονική στιγμή t=10s, αν η ενέργεια της ταλάντωσης μειώνεται εκθετικά σε σχέση με το χρόνο σύμφωνα με τη σχέση Ε=10 ·e-2Λt(J). Μονάδες 5
............................................................................................................................
B. Ένας δίσκος ακτίνας r=0,1m, που έχει κολλημένο στην περιφέρειά του ένα μικρό σώμα, μάζας m=10g, μπορεί να περιστρέφεται γύρω από ακλόνητο άξονα, που διέρχεται από το κέντρο του και είναι κάθετος στο δίσκο. Η μέγιστη ελκτική δύναμη μεταξύ του δίσκου και του σώματος είναι 6,4Ν. Αρχικά ο δίσκος είναι ακίνητος. Τη χρονική στιγμή t0=0s ασκείται στο δίσκο κατάλληλη δύναμη, με αποτέλεσμα ο δίσκος να αποκτήσει σταθερή γωνιακή επιτάχυνση μέτρου αγων=8rad/s2. Να υπολογίσετε:
B1) τη γωνιακή ταχύτητα που πρέπει να αποκτήσει ο δίσκος για να αποσπαστεί το σώμα από την περιφέρεια του δίσκου. Μονάδες 5
B2) τη στροφορμή του σώματος, τη στιγμή που αποσπάται. Μονάδες 5
............................................................................................................................
Γ.
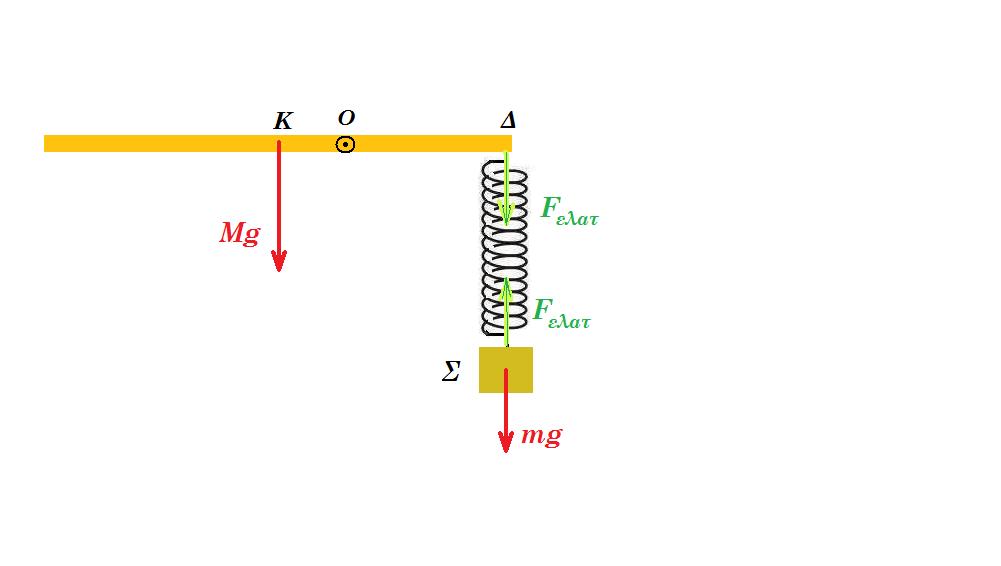
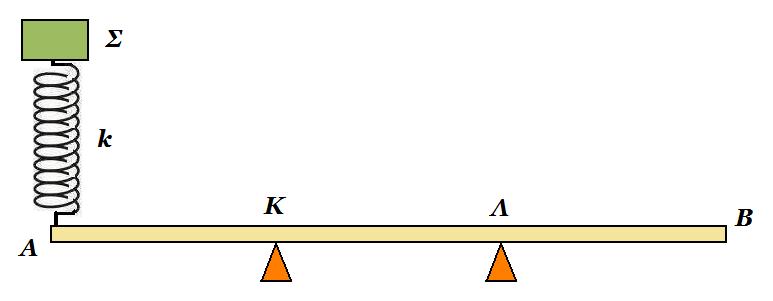 Η ομογενής δοκός ΑΒ του σχήματος, μήκους ℓ=3m και μάζας Μ=20kg ισορροπεί σε οριζόντια θέση, στηριζόμενη σε δύο στηρίγματα στα σημεία Κ και Λ, όπου (ΑΚ)=(ΚΛ)= (ΛΒ)=1m. Στο άκρο Α έχει στερεωθεί ιδανικό ελατήριο σταθεράς k=100Ν/m, στο πάνω άκρο του οποίου ισορροπεί σώμα Σ, μάζας m=4kg.
Η ομογενής δοκός ΑΒ του σχήματος, μήκους ℓ=3m και μάζας Μ=20kg ισορροπεί σε οριζόντια θέση, στηριζόμενη σε δύο στηρίγματα στα σημεία Κ και Λ, όπου (ΑΚ)=(ΚΛ)= (ΛΒ)=1m. Στο άκρο Α έχει στερεωθεί ιδανικό ελατήριο σταθεράς k=100Ν/m, στο πάνω άκρο του οποίου ισορροπεί σώμα Σ, μάζας m=4kg.
Γ1. Να υπολογιστούν οι δυνάμεις που δέχεται η δοκός από τα δύο στηρίγματα. Μονάδες 10
Γ2. Μετακινούμε το σώμα Σ κατακόρυφα προς τα κάτω κατά d=0,5m και τη στιγμή t=0, το αφήνουμε να ταλαντωθεί. Θεωρούμε την προς τα κάτω κατεύθυνση θετική.
- Να γράψετε τη συνάρτηση που περιγράφει τη δύναμη που ασκεί το ελατήριο στο σώμα Σ σε σχέση με την απομάκρυνση , τη συνάρτηση που περιγράφει τη δυναμική ενέργεια του ελατηρίου σε σχέση με την απομάκρυνση και τη συνάρτηση που περιγράφει τη δυναμική ενέργεια της ταλάντωσης του σώματος σε σχέση με την απομάκρυνση. Να παραστήσετε γραφικά κάθε σχέση σε αριθμημένους άξονες. Μονάδες 15
- Να γράψετε τη συνάρτηση που περιγράφει τη συνάρτηση που περιγράφει τη δυναμική ενέργεια της ταλάντωσης του σώματος σε σχέση με τον χρόνο και παραστήστε γραφικά την σχέση σε αριθμημένους άξονες. Μονάδες 5
- Να εκφράσετε τις δυνάμεις αντίδρασης Ν1 και Ν2 στα σημεία Κ και Λ αντίστοιχα συναρτήσει του χρόνου. Ποιά είναι η μέγιστη και η ελάχιστη τιμή της αντίδρασης Ν2, που δέχεται η δοκός από το στήριγμα στο σημείο Λ; Δίνεται g=10m/s2. Μονάδες 10
............................................................................................................................
Δ.
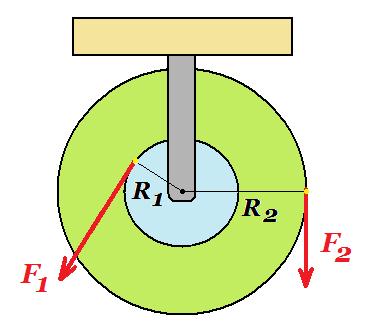
Η διπλή τροχαλία του σχήματος μπορεί να στρέφεται γύρω από σταθερό άξονα που συμπίπτει με τον άξονα συμμετρίας της. Η τροχαλία έχει ακτίνες, R1=10cm, R2=20cm και είναι αρχικά ακίνητη. Μέσω κατάλληλων αβαρών νημάτων ασκούνται στην τροχαλία οι δυνάμεις F1=60N και F2=40N, αντίστοιχα, με σημεία εφαρμογής και κατευθύνσεις, όπως δείχνονται στο σχήμα. Η τροχαλία αποκτά γωνιακή επιτάχυνση ίση με αγων=2rad/s2. Να υπολογίσετε:
Δ1) τη συνολική ροπή που δέχεται η τροχαλία. Μονάδες 5
Δ2) τη γωνιακή ταχύτητα της τροχαλίας τη χρονική στιγμή t=4s. Μονάδες 5
Δ3) το μήκος του νήματος που έχει τυλιχτεί ή ξετυλιχτεί σε κάθε τροχαλία, τη χρονική στιγμή t=4s. Μονάδες 5
Δ4) τη γωνία που διέγραψε η τροχαλία από τη χρονική στιγμή t1=2s μέχρι τη χρονική στιγμή t2=4s. Μονάδες 5
............................................................................................................................
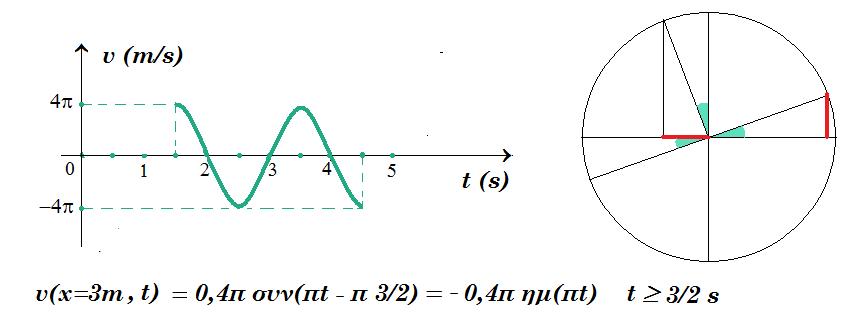
E. Κατά μήκος ενός γραμμικού ελαστικού μέσου διαδίδεται προς την θετική κατεύθυνση ένα αρμονικό κύμα, πλάτους Α=0,4m με ταχύτητα 2m/s. Την χρονική στιγμή t=0, το κύμα φτάνει στην αρχή Ο ενός προσανατολισμένου άξονα, το οποίο αρχίζει να ταλαντώνεται, κινούμενο προς τα πάνω (θετική απομάκρυνση) με περίοδο Τ=2s.
E1) Να γράψετε την εξίσωση του διαδιδόμενου κύματος. Μονάδες 5
E2) Να σχεδιάσετε το στιγμιότυπο του κύματος την χρονική στιγμή t1=4,5s και σχεδιάστε τη γραφική παράσταση της φάσης φ συναρτήσει της απόστασης χ την ίδια στιγμή. Μονάδες 5
E. (α) ω = 2π/Τ = 2π/2 = π rad/s v = λ/T => λ = v T = 2 m/s 2 s = 4 m
y(x,t) = 0,4 ημ 2π (t/2 - x/4) = 0,4 ημ(πt - πx/2) v(x,t) = 0,4π συν(πt - πx/2) α(x,t) = 0,4π2 ημ(πt - πx/2)
(β) y = 0,4 ημ π(4,5 - x/2) = 0,4 συν(πx/2) y = 0 => x = 9 m = 2 m/s 4,5 s = v t
Τ = 2s t1 = 4,5s = 2T + T/4 δύο περίοδοι + 1/4 της περιόδου
φ = 4,5π - πx/2 v(x=3m , t=4,5s) = 0,4π συν(π 4,5 - π 3/2) = 0,4π συν(3π) = - 0,4π m/s
v(x=3m , t) = 0,4π συν(πt - π 3/2) = - 0,4π ημ(πt)

Δ. Στ = F1 R1 - F2 R2 = 60 N 0,1 m - 40 N 0,2 m = - 2 Nm
ω = αγων t = 2 rad/s2 4 s = 8 rad/s
l1 = θ R1 = ½ αγων t2 R1 = ½ 2 rad/s2 16 s2 0,1 m = 1,6 m
l2 = θ R2 = ½ αγων t2 R2 = ½ 2 rad/s2 16 s2 0,2 m = 3,2 m
Δθ = ½ αγων t22 - ½ αγων t12 = ½ 2 rad/s2 16 s2 - ½ 2 rad/s2 4 s2 = => Δθ = 12 rad
............................................................................................................................
B. ω = αγων t => Δω = αγων Δt = 8rad/s2 ( 6s - 2s ) = 32 rad/s
Fκ = m v2 / r => 6,4 = 0,01 υ2 / 0,1 => υ2 = 64 => υ = 8 m/s ω = υ/r = 8 / 0,1 = 80 rad/s
L = m v r = 0,01 8 0,1 = 0,008 kg m2/s
ω = αγων t => t = 80 rad/s / 8rad/s2 = 10 s θ = ½ αγων t2 = ½ 8rad/s2 100 s2 = 400 rad
s = r θ = 0,1 400 = 40 m ή αλλιώς s = ½ α t2 = ½ r αγων t2 = ½ 0,1 8 102 = 40 m
............................................................................................................................
Γ. θετική κατεύθυνση : κατακόρυφη προς τα κάτω
ισορροπία Σ : mg + F'ελατ = 0 => F'ελατ = - 40 Ν και στο άλλο άκρο του ελατηρίου : Fελατ = - F'ελατ = + 40 Ν
F'ελατ = k Δl => Δl = 40 / 100 = 0,4 m αρχική συσπείρωση ελατηρίου
ισορροπία δοκού : Μg + Fελατ - Ν1 - Ν2 = 0 => Ν1 + Ν2 = 200 + 40 => Ν1 + Ν2 = 240 Ν
ροπές ως προς Κ : Στ(Κ) = 0 => Fελατ (ΑΚ) + Ν2 (ΚΛ) - Μg ( ℓ/2 - ΑΚ ) = 0 => 40 1 + Ν2 1 - 200 0,5 = 0 => Ν2 = 60 Ν
ροπές ως προς Λ : Στ(Λ) = 0 => Fελατ (ΑΛ) - Ν1 (ΚΛ) + Μg ( ℓ/2 - ΒΛ ) = 0 => 40 2 - Ν1 1 + 200 0,5 = 0 => Ν1 = 180 Ν
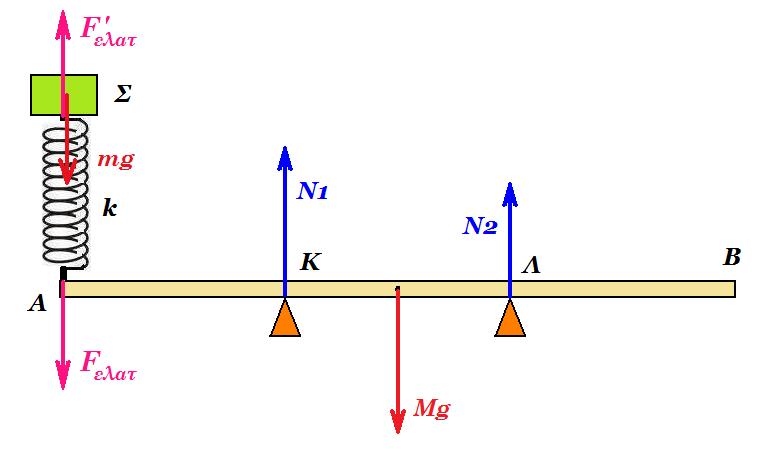
ω2 = k / m = 100 / 4 = 25 => ω = 5 rad/s T = 2π/ω = 2π/5 s
x(t) = 0,5 ημ(5t + π/2) v(t) = 2,5 συν(5t + π/2) α(t) = - 12,5 ημ(5t + π/2)
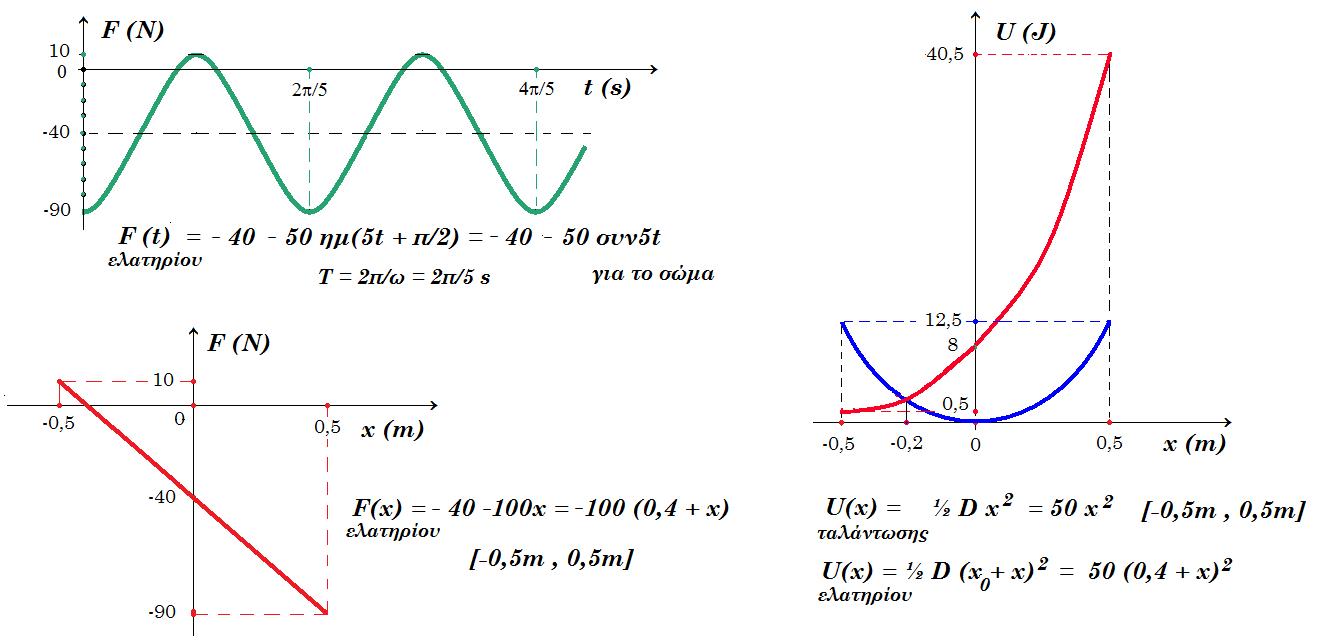
ΣF = ma => F'ελατ + mg = ma => F'ελατ (t) = - 40 - 50 ημ(5t + π/2) για το σώμα
και Fελατ (t) = 40 + 50 ημ(5t + π/2) για την δοκό
ΣF = - D x => Fελατ + mg = - D x => Fελατ(x) = - 40 - 100x = - 100 (0,4 + x) [-0,5m , 0,5m] Fελατ(0) = - 40 N
Uταλάντωσης = ½ D x2 = ½ 100 x2 = 50 x2 [-0,5m , 0,5m]
Uελατηρίου = ½ D (x0 + x)2 = ½ 100 (0,4 + x)2 = 50 (0,4 + x)2 [-0,5m , 0,5m]
x = 0,5 m Fελατ = - 90 Ν Uταλάντωσης = 50 0,52 = 12,5 J Uελατηρίου = 50 (0,4 + 0,5)2 = 40,5 J
x = 0 m Fελατ = - 40 Ν Uταλάντωσης = 0 Uελατηρίου = 50 (0,4)2 = 8 J
x = - 0,5 m Fελατ = +10 Ν Uταλάντωσης = 50 (-0,5)2 = 12,5 J Uελατηρίου = 50 (0,4 - 0,5)2 = 0,5 J
Uταλάντωσης = ½ D x2 = ½ 100 ( 0,5 ημ(5t + π/2) )2 = 12,5 ημ2(5t + π/2) = 12,5 { 0,5 - 0,5 συν(10t + π) } = 6,25 - 6,25 συν(10t + π) = 6,25 - 6,25 συν(10t + π) = 6,25 + 6,25 συν(10t) 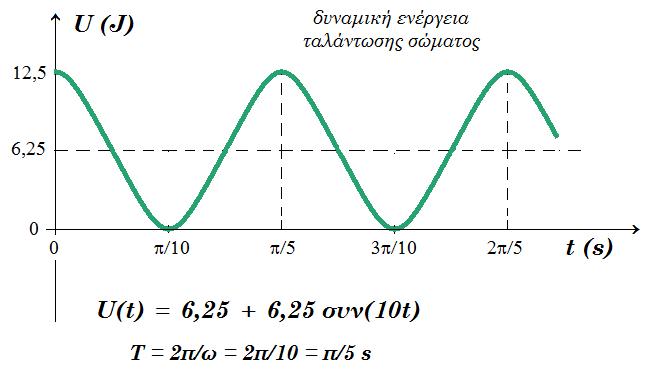
Uελατηρίου = ½ D (x0 + x)2 = ½ 100 ( 0,4 + 0,5 ημ(5t + π/2) )2 = 50 ( 0,16 + 0,25 ημ2(5t + π/2) + 2 0,4 0,5 ημ(5t + π/2) ) = 50 ( 0,16 + 0,25 [ 0,5 - 0,5 συν(10t + π) ] + 0,4 ημ(5t + π/2) ) = 50 ( 0,16 + 0,125 - 0,125 συν(10t + π) ] + 0,4 ημ(5t + π/2) )
= 8 + 6,25 - 6,25 συν(10t + π) + 20 ημ(5t + π/2) = 14,25 + 6,25 συν(10t) + 20 συν(5t)
ημ2(5t + π/2) = 0,5 - 0,5 συν(10t + π) συν2α = συν2α - ημ2α = 1 - ημ2α - ημ2α = 1 - 2ημ2α
συν(10t + π) = συν(10t) συνπ - ημ(10t) ημπ = - συν(10t) ημ(5t + π/2) = ημ(5t) συν(π/2) + συν(5t) ημ(π/2) = συν(5t)
ροπές ως προς Λ : Στ(Λ) = 0 => Fελατ (ΑΛ) - Ν1 (ΚΛ) + Μg ( ℓ/2 - ΒΛ ) = 0 =>
=> ( 40 + 50 ημ(5t + π/2) ) 2 - Ν1 1 + 200 0,5 = 0 => Ν1(t) = 180 + 100 ημ(5t + π/2) κατακόρυφη προς τα πάνω
Μg + Fελατ - Ν1 - Ν2 = 0 => 200 + 40 + 50 ημ(5t + π/2) - Ν2 - ( 180 + 100 ημ(5t + π/2) ) = 0 =>
=> 60 - Ν2 - 50 ημ(5t + π/2) = 0 => Ν2(t) = 60 - 50 ημ(5t + π/2) κατακόρυφη προς τα πάνω
ροπές ως προς Κ : Στ(Κ) = 0 => Fελατ (ΑΚ) + Ν2 (ΚΛ) - Μg ( ℓ/2 - ΑΚ ) = 0 =>
=> ( 40 + 50 ημ(5t + π/2) ) 1 + Ν2 1 - 200 0,5 = 0 => Ν2(t) = 60 - 50 ημ(5t + π/2)
Ν1(t) + Ν2(t) = 180 + 100 ημ(5t + π/2) + 60 - 50 ημ(5t + π/2) = 240 + 50 ημ(5t + π/2) =
= 200 + 40 + 50 ημ(5t + π/2) = Μ g + Fελατ (t) επαλήθευση
t = 0 Ν2(0) = 60 - 50 ημ(π/2) = 60 - 50 = 10 N ελάχιστη δύναμη κατακόρυφη προς τα πάνω
Ν1(0) = 180 + 100 ημ(π/2) = 280 Ν κατακόρυφη προς τα πάνω
Fελατ = 40 + 50 ημ(π/2) = 40 + 50 = 90 Ν και
F'ελατ = - 90 N το ελατήριο συσπειρώνεται κατά 90 Ν / 100 N/m = 0,9 m
στη δοκό ασκούνται Ν1 = 280 Ν & Ν2 = 10 Ν προς τα πάνω και Fελατ = 90 Ν & βάρος = 200 Ν προς τα κάτω
t = T/4 = π/10 s Ν2 = 60 - 50 ημ(5 π/10 + π/2 ) = 60 - 50 ημ(π) = 60 Ν
Ν1 = 180 + 100 ημ(5 π/10 + π/2) = 180 Ν
Fελατ = 40 + 50 ημ(5 π/10 + π/2) = 40 + 50 ημπ = 40 Ν = mg και
F'ελατ = - 40 N το ελατήριο συσπειρώνεται κατά 40 Ν / 100 N/m = 0,4 m
t = T/2 = π/5 s Ν2 = 60 - 50 ημ(5 π/5 + π/2 ) = 60 - 50 ημ(3π/2) = 110 N μέγιστη δύναμη κατακόρυφη προς τα πάνω
Ν1 = 180 + 100 ημ(5 π/5 + π/2) = 180 - 100 = 80 Ν κατακόρυφη προς τα πάνω
Fελατ = 40 + 50 ημ(5 π/5 + π/2) = 40 + 50 ημ(3π/2) = 40 - 50 = - 10 Ν και
F'ελατ = + 10 N το ελατήριο επιμηκύνεται κατά 10 Ν / 100 N/m = 0,1 m
............................................................................................................................
Α. f = 5cycle / 10s = 0,5 Hz T = 1/f = 2 s
A = A0 e-Λt => A0/2 = A0 e-Λ 10s => 1/2 = e-Λ 10s => 2 = eΛ 10s => ln2 = Λ 10s => Λ = ln2/10 s-1
5 ταλαντώσεις 10 s => 15 ταλαντώσεις 30 s
A = A0 e-Λ 30s = A0 e( -ln2/10 ) 30 = A0 e -3 ln2 = A0 exp { ln2-3 } = A0 2-3 = 10cm / 8 = 1,25 cm
A = A0 e-Λt => 2,5 cm = 10 cm e-Λt => 0,25 = 1/4 = 1/22 = e-Λt => 22 = eΛt => ln22 = Λt => 2ln2 = ln2/10 t => t = 20s
E = 10 e-2Λt = 10 exp { -2 ln2/10 10 } = 10 exp { ln2-2 } = 10 2-2 = 10 1/4 = 2,5 J
W = E -E0 = 2,5 J - 10 J = - 7,5 J
ΘΕΜΑ Α

Ο τροχός κυλίεται πάνω σε οριζόντιο επίπεδο. Αν το άκρο Α του οριζοντίου νήματος έχει επιτάχυνση 4 m/s2 βρείτε την επιτάχυνση του ανώτερου σημείου Ε του τροχού.
ΘΕΜΑ Β
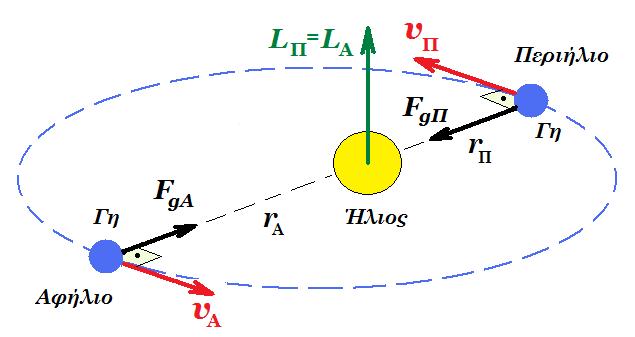
B1. Η Γη περιστρέφεται γύρω από τον Ήλιο σε ελλειπτική τροχιά. Θεωρούμε ότι η μόνη δύναμη που δέχεται είναι η βαρυτική έλξη 𝐹⃗𝑔 από τον Ήλιο. Το σημείο της ελλειπτικής τροχιάς της Γης που βρίσκεται στη μικρότερη απόσταση, 𝑟𝛱, από τον Ήλιο ονομάζεται περιήλιο, ενώ το σημείο που βρίσκεται στη μεγαλύτερη απόσταση, 𝑟𝐴, ονομάζεται αφήλιο. 
Η σχέση που συνδέει τις δύο αποστάσεις είναι: 𝑟𝛱 = 0,9 𝑟𝛢. Η σχέση που συνδέει το μέτρο της γωνιακής ταχύτητας της Γης στο περιήλιο, 𝜔𝛱, με το μέτρο της στο αφήλιο, 𝜔𝛢, είναι:
(α) 𝜔𝛱 = 𝜔𝛢 (β) 𝜔𝛱 = 100/81 𝜔𝛢 (γ) 𝜔𝛱 = 0,81 𝜔𝛢
Β1 (α). Να επιλέξετε την ορθή απάντηση. Μονάδες 3
Β1 (β). Να αιτιολογήσετε την επιλογή σας. Μονάδες 7
B2. Σε ένα υποθετικό πείραμα, κρεμάσαμε κατακόρυφα δύο διαφορετικά ιδανικά ελατήρια που έχουν το ίδιο φυσικό μήκος, στερεώνοντας το πάνω άκρο τους στο ίδιο οριζόντιο, ακλόνητο επίπεδο. Στο ένα ελατήριο σταθεράς 𝑘1, κρεμάσαμε ένα σώμα 𝛴1 μάζας 𝑚1 και φροντίσαμε να ισορροπεί ακίνητο. Στο άλλο ελατήριο σταθεράς 𝑘2, κρεμάσαμε άλλο σώμα 𝛴2, μάζας 𝑚2 και φροντίσαμε να ισορροπεί και αυτό ακίνητο. Μετρήσαμε ότι καθώς τα δύο σώματα ισορροπούν, έχουν προκαλέσει ίσες επιμηκύνσεις στα δύο ελατήρια (𝛥𝑙1 = 𝛥𝑙2).
Εκτρέπουμε και τα δύο συστήματα από την κατάσταση ισορροπίας, τραβώντας κατακόρυφα προς τα κάτω το σώμα κάθε συστήματος και κάποια στιγμή το αφήνουμε ελεύθερο να ταλαντώνεται. Για το χρονικό διάστημα των παρατηρήσεων, μπορούμε να αγνοήσουμε τις αντιστάσεις του αέρα, με αποτέλεσμα κάθε σύστημα να εκτελεί κατακόρυφη απλή αρμονική ταλάντωση, με σταθερά επαναφοράς την σταθερά του ελατηρίου. Μετρώντας το χρόνο για ένα πλήθος ταλαντώσεων κάθε συστήματος, μπορούμε να υπολογίσουμε τη συχνότητα ταλάντωσης. Για τις συχνότητες 𝑓1, 𝑓2 των συστημάτων (1) και (2) αντίστοιχα, θα προκύψει η σχέση: (α) 𝑓1 = 𝑓2 (β) 𝑓1 = 4∙𝑓2 (γ) 𝑓1 = 𝑓2/4
Β2 (α). Να επιλέξετε την ορθή απάντηση. Μονάδες 3
Β2 (β). Να αιτιολογήσετε την επιλογή σας. Μονάδες 7
Β3. Δύο σφαίρες 𝛴1, 𝛴2, με μάζες 𝑚1 και 𝑚2 αντίστοιχα, είναι αρχικά ακίνητες σε λείο οριζόντιο, ακλόνητο δάπεδο, έτσι ώστε τα κέντρα τους να ορίζουν μια οριζόντια ευθεία κάθετη σε κατακόρυφο τοίχο. Εκτοξεύουμε τη σφαίρα 𝛴1 με οριζόντια ταχύτητα 𝜐⃗1, τέτοια ώστε να πλησιάζει τη σφαίρα 𝛴2 και να απομακρύνεται από τον τοίχο. Η κρούση μεταξύ των δύο σφαιρών είναι κεντρική και ελαστική και η 𝛴1 μετά την κρούση της με τη 𝛴2 συγκρούεται με τον τοίχο, με κρούση επίσης ελαστική. Αν δίνεται ότι οι δύο σφαίρες δεν θα συγκρουστούν για δεύτερη φορά, τότε για τις μάζες τους είναι δυνατόν να ισχύει η σχέση: (α) 𝑚2 = 𝑚𝟏 (β) 𝑚2 = 2∙𝑚1 (γ) 𝑚2 = 4∙𝑚1
Β3 (α). Να επιλέξετε την ορθή απάντηση. Μονάδες 3
Β3 (β). Να αιτιολογήσετε την επιλογή σας. Μονάδες 7
 Σωστή απάντηση είναι η (β) Μονάδες 4 24444
Σωστή απάντηση είναι η (β) Μονάδες 4 24444
Η Γη περιστρέφεται γύρω από τον Ήλιο σε ελλειπτική τροχιά. Η μόνη δύναμη που δέχεται η Γη είναι η βαρυτική έλξη 𝐹⃗𝑔 από τον Ήλιο. Η δύναμη αυτή είναι κεντρική, δηλαδή ο φορέας της περνά από τον Ήλιο, επομένως η ροπή της ως προς τον Ήλιο είναι μηδέν, 𝛴𝜏 = 0. Θεωρώντας τη Γη σημειακή μάζα σε σχέση με τον Ήλιο συμπεραίνουμε ότι η στροφορμή της, ως προς τον άξονα που περνά από τον Ήλιο και είναι κάθετος στο επίπεδο περιστροφής, παραμένει σταθερή κατά την περιστροφή της. Δηλαδή:
𝐿𝛱 = 𝐿𝛢 ⇒ 𝛭𝛤 ∙ 𝜐𝛱 ∙ 𝑟𝛱 = 𝛭𝛤 ∙ 𝜐𝛢 ∙ 𝑟𝐴 ⇒ 𝜔𝛱 ∙ 𝑟𝛱 ∙ 𝑟𝛱 = 𝜔𝛢 ∙ 𝑟𝛢 ∙ 𝑟𝛢 ⇒ 𝜔𝛱 = 𝜔𝛢 ∙ (𝑟𝛢 / 𝑟𝛱)2 Επομένως, 𝜔𝛱 = 100/81 𝜔𝛢 Μονάδες 9
Tο σώμα Β του σχήματος είναι ακίνητο πάνω σε λείο οριζόντιο δάπεδο και δεμένο στην άκρη ιδανικού ελατηρίου. Το σώμα Α, μάζας mA κινούμενο με ταχύτητα υΑ=3m/s κατά μήκος του άξονα του ελατηρίου, συγκρούεται κεντρικά με το σώμα Β τη χρονική στιγμή t=0. Οι αλγεβρικές τιμές των ταχυτήτων των σωμάτων μετά την κρούση (θετική φορά προς τα αριστερά) φαίνονται στο διάγραμμα ταχυτήτων-χρόνου.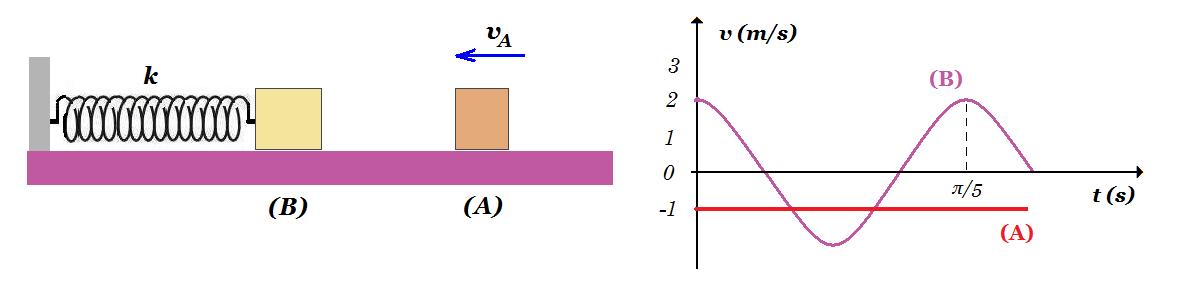
Οι μάζες των σωμάτων Α και Β συνδέονται με τη σχέση : α) mA = mB β) mB = 2mA γ) mΑ = 2mΒ
Είναι η κρούση ελαστική;
ΘΕΜΑ Γ
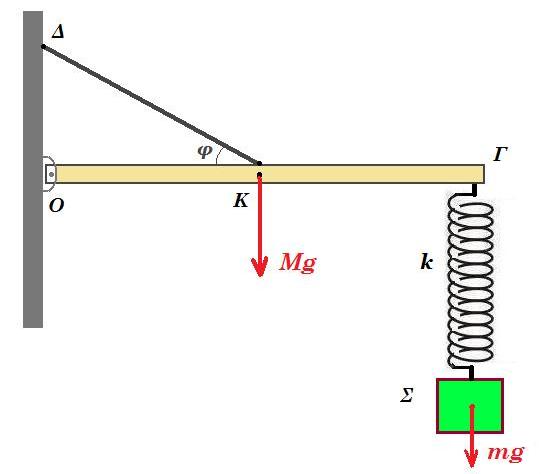
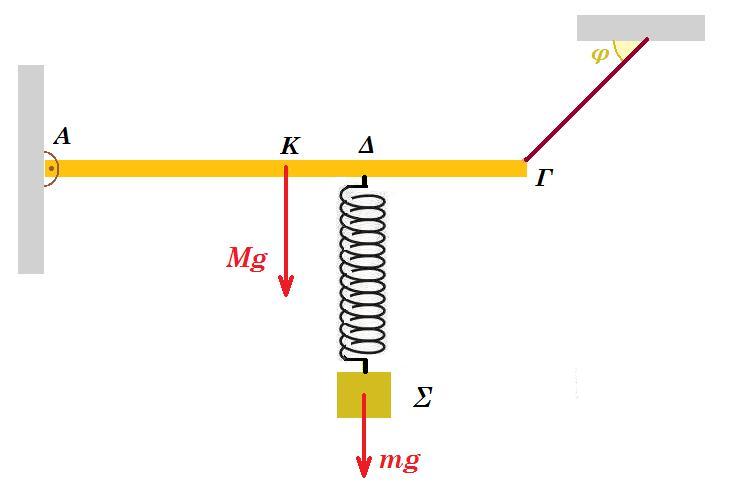
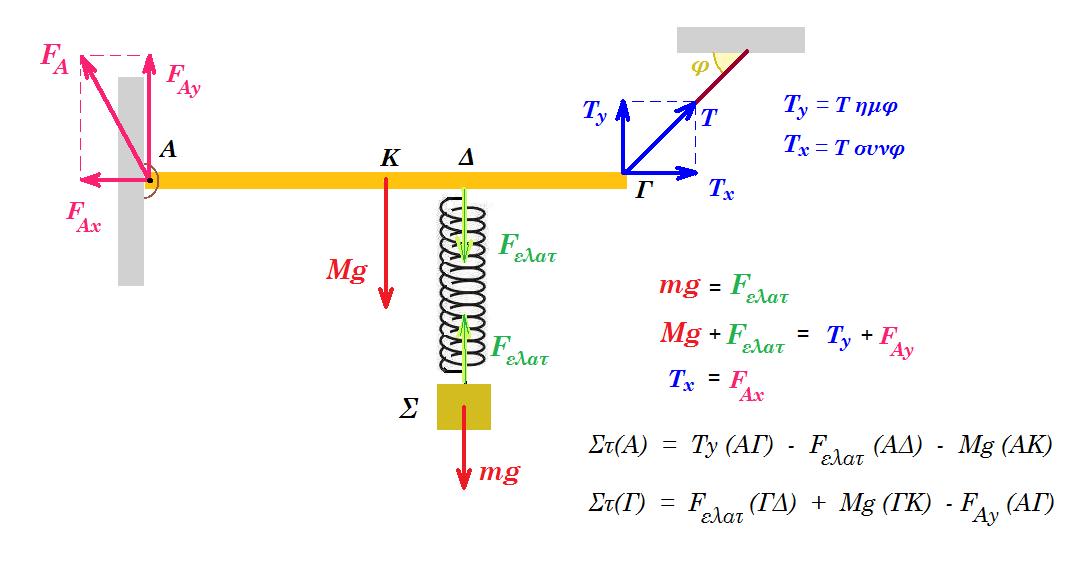
M = 8 kg, m = 6 kg, k = 150 N/m, ημφ = 0,6 συνφ = 0,8 l = 4 m = (ΟΓ) = 2 (ΟΚ) = 2 (ΚΓ) 8202 = 672400
Η διάταξη βρίσκεται σε ισορροπία σε κατακόρυφο επίπεδο. Γ1.) Υπολογίστε την δύναμη που δέχεται η οριζόντια δοκός ΟΓ στην άρθρωση στο άκρο της Ο.
Γ2.) Δίνουμε στο σώμα Σ κατακόρυφη προς τα πάνω ταχύτητα μέτρου υ = 2 m/s εκφράστε τις δυνάμεις που ασκούνται στη δοκό στα στηρίγματα συναρτήσει του χρόνου.
...................................................................................................................................

ισορροπία σώματος Σ : m g = Fελατ = k x0 => x0 = m g / k = 6 10 / 150 => x0 = 0,4 m αρχική επιμήκυνση ελατηρίου
στο άκρο Γ η δοκός δέχεται κατακόρυφη προς τα κάτω δύναμη από το ελατήριο FΓ = Fελατ = m g = 60 Ν
ροπές ως προς Ο : Τy l /2 - M g l /2 - FΓ l = 0 => Τy = M g + 2 FΓ = 80 + 120 = 200 N
Τ = Τy / ημφ = 200 Ν / 0,6 => Τ = 1000/3 Ν τάση νήματος Tx = T συνφ = 1000/3 Ν 0,8 = 800/3 Ν
επαλήθευση : (800/3)2 + 2002 = 640000/9 + 40000 = ( 640000 + 360000 ) / 9 = 1000000 / 9 = (1000/3)2
ροπές ως προς Κ : Fy(O) l/2 - FΓ l/2 = 0 => Fy(O) = FΓ = Fελατ = m g = 60 Ν
ΣFy = 0 => Fy(O) + Ty = M g + FΓ => Fy(O) = - 200 + 80 + 60 => Fy(O) = - 60 N δηλαδή |Fy(O)|= 60 N προς τα κάτω
ΣFx = 0 => Fx(O) - Tx = 0 => Fx(O) = 800/3 N
ΣF(O)2 = Fx(O)2 + Fy(O)2 = 602 + (800/3)2 = 3600 + 640000/9 = ( 32400 + 640000 ) / 9 = 672400 / 9 => => ΣF(O) = 820/3 Ν
k = m ω2 => 150 = 6 ω2 => ω2 = 25 => ω = 5 rad/s f = ω/2π = 5/2π Hz T = 1/f = 2π/5 s
υ = ω A => υ = 5 rad/s 0,4 m => υ = 2 m/s θετική κατεύθυνση κατακόρυφη προς τα πάνω
x = A ημωt = 0,4 ημ5t υ = 0,4 5 συν5t = 2 συν5t α = - 10 ημ5t
ΣF = m α = 6 ( - 10 ημ5t ) = - 60 ημ5t = Fελατ - m g => Fελατ = 60 - 60 ημ5t
FΓ = - Fελατ = - 60 + 60 ημ5t
ροπές ως προς Ο : Στ(Ο) = 0 => Τy l /2 + ( - M g l/2 ) + FΓ l = 0 =>
=> Τy = M g - 2 FΓ = 80 - 2 ( - 60 + 60 ημ5t ) => Ty = 200 - 120 ημ5t = Τ ημφ = 0,6 T =>
=> Τ = ( 200 - 120 ημ5t ) / 0,6 => T = 1000/3 - 200 ημ5t
Tx = T συνφ = ( 1000/3 - 200 ημ5t ) 0,8 = 800/3 - 160 ημ5t
Ty2 + Tx2 = 40000 - 48000 ημ5t + 14400 (ημ5t)2 + 640000/9 + 25600 (ημ5t)2 - 2560000/3 ημ5t = (1000/3)2 + 2002 (ημ5t)2 - 400000/3 ημ5t = ( 1000/3 - 200 ημ5t )2 = T2
ροπές ως προς Κ : Στ(Κ) = 0 => Fy(Ο) l/2 - FΓ l/2 = 0 => Fy(O) = FΓ = - 60 + 60 ημ5t
ΣFy = 0 => Fy(O) + Ty + ( - M g ) + FΓ = 0 => Fy(O) = - Ty - ( - M g ) - FΓ =>
=> Fy(O) = - 200 + 120 ημ5t + 80 + 60 - 60 ημ5t => Fy(O) = - 60 + 60 ημ5t = FΓ = - Fελατ
ΣFx = 0 => Fx(O) + Tx = 0 => Fx(O) = - Tx = - 800/3 + 160 ημ5t
t = T/4 = 2π/5 / 4 => t = π/10 s
Fελατ = 60 - 60 ημ5t = 60 - 60 ημ(π/2) = 0 = FΓ
Ty = - 40 + 120 ημ5t = - 40 + 120 ημ(π/2) = 80 Ν = M g
Tx = - 160/3 + 160 ημ5t = - 160/3 + 160 = 320/3 Ν = Fx(O)
Fy(O) = 60 - 60 ημ5t = 60 - 60 = 0
 εκφράστε τις δυνάμεις που ασκούνται στη δοκό στα στηρίγματα συναρτήσει της γωνίας θ που σχηματίζει το νήμα με την κατακόρυφο
εκφράστε τις δυνάμεις που ασκούνται στη δοκό στα στηρίγματα συναρτήσει της γωνίας θ που σχηματίζει το νήμα με την κατακόρυφο
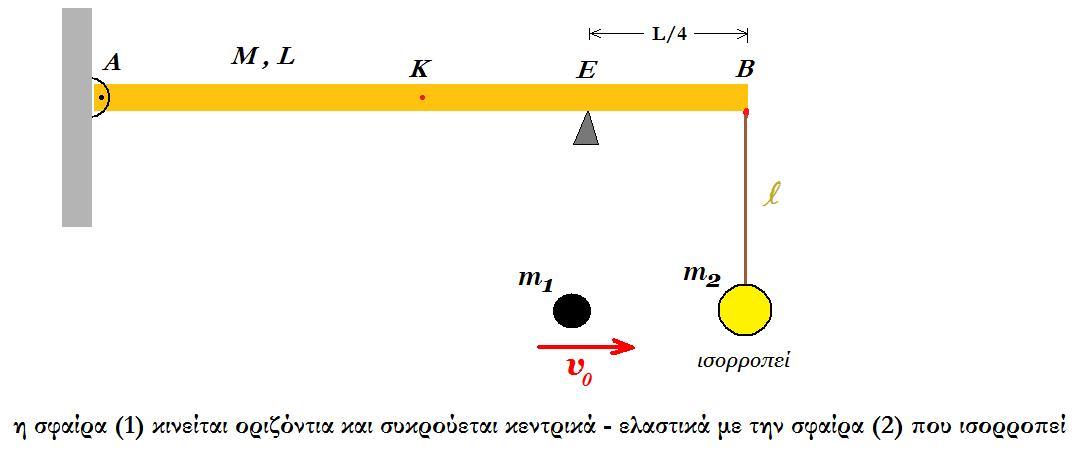
m1 = 3 kg m2 = 1 kg υ0 = 4 m/s M = 6 kg L = 4 m l = 1 m
v1 = (m1 - m2) v0 / (m1 + m2) = (3 - 1) 4 / (3 + 1) = 2 m/s v2 = 2 m1 v0 / (m1 + m2) = 2 3 4 / (3 + 1) = 6 m/s
h = v22 / 2g = 36 / 20 = 1,8 m μέγιστο ύψος h = 1,8 m < 2l = 2 m άρα το σώμα m2 δεν κάνει ανακύκλωση
το σώμα m2 σε τυχαία θέση : v22 = v2 + 2 g l (1 - συνθ) => 36 = v2 + 20 (1 - συνθ) => v2 = 20 συνθ + 16
υ = 0 <=> συνθ = - 16 / 20 = - 0,8
ΣF = FΚ => Τ - m2 g συνθ = m2 v2 / l => Τ = m2 g συνθ + m2 v2 / l => T = 10 συνθ + 20 συνθ + 16 = 30 συνθ + 16
η τάση του νήματος μηδενίζεται όταν 30 συνθ = - 16 => συνθ = - 8/15
|wy| = w|συνθ| = m2 g |συνθ| = 1 10 |-8/15| = 16/3 N
FK = m2 v2 / l = 1 ( 20 συνθ + 16 ) / 1 = 20 (-8/15) + 16 = -32/3 + 16 = (-32 + 48) / 3 = 16/3 N
όταν συνθ = -8/15 τότε το νήμα δεν ασκεί δύναμη στο σώμα m2 και τον ρόλο της κεντρομόλου δυνάμεως παίζει η συνιστώσα του βάρους wy
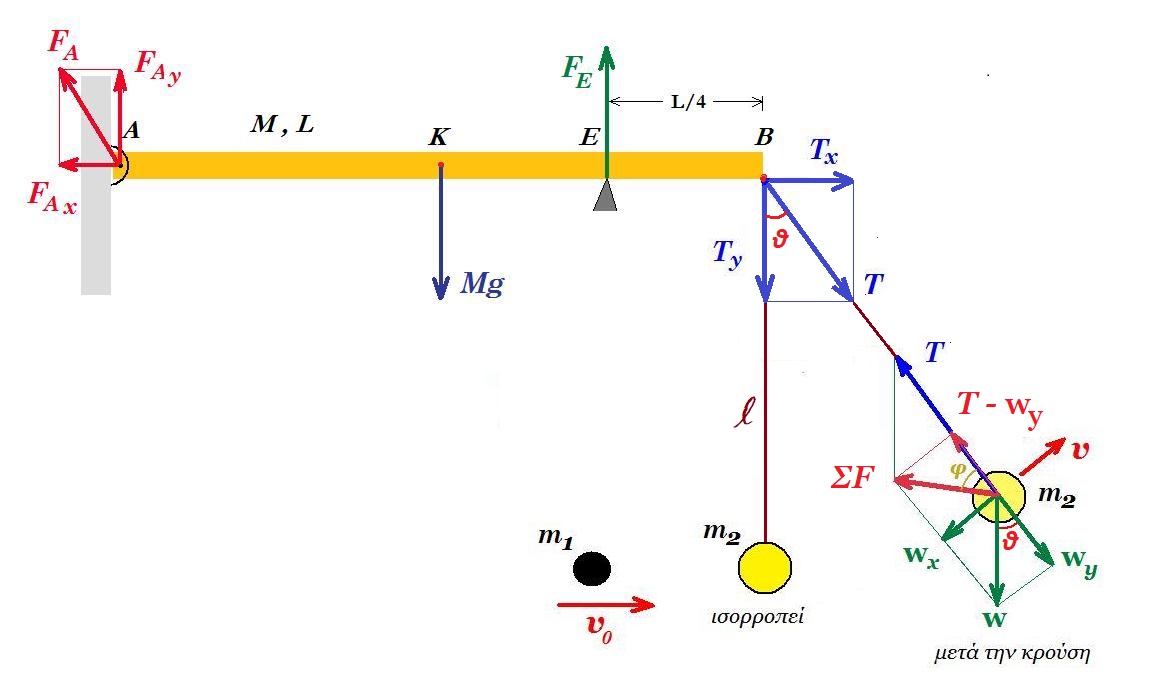
ισορροπία δοκού
ΣFx = 0 => FAx = Tx = Τ ημθ (1) ΣFy = 0 => M g + Ty = FAy + FE => 60 + Ty = FAy + FE (2)
Στ(Α) = 0 => FE 3L/4 = Mg L/2 + Ty L => 3 FE = 2 Mg + 4 Ty => 3 FE = 120 + 4 Ty (3)
Στ(Ε) = 0 => Mg L/4 = FAy 3L/4 + Ty L/4 => Mg = 3 FAy + Ty => 60 = 3 FAy + Ty (4)
Στ(Β) = 0 => Mg L/2 = FE L/4 + FAy L => 60 /2 = FE /4 + FAy => 120 = FE + 4 FAy (5)
η (3) => FE = 40 + 4/3 T συνθ = 40 + 4/3 ( 30 συνθ + 16 ) συνθ
η (4) => FAy = 20 - 1/3 T συνθ = 20 - 1/3 ( 30 συνθ + 16 ) συνθ Tx = T ημθ = 8 0,6 = 4,8 Ν Τy = T συνθ = 8 0,8 = 6,4 Ν
Στ(Ε) = 0 => Mg L/4 = FAy 3L/4 + Ty L/4 => 60 = 3 FAy + 6,4 => FAy = 53,6/3 Ν
Στ(Α) = 0 => FE 3L/4 = Mg L/2 + Ty L => 3 FE = 2 Mg + 4 Ty => 3 FE = 120 + 4 6,4 => FE = 145,6/3 Ν
όταν θ = 90° τότε συνθ = 0 και ημθ = 1
(1) => FAx = Tx = Τ ημθ = ( 30 συνθ + 16 ) ημθ = ( 30 0 + 16 ) 1 = 16 Ν
FE = 40 + 4/3 ( 30 συνθ + 16 ) συνθ = 40 + 4/3 ( 30 0+ 16 ) 0 = 40 Ν
FΑy = 20 - 1/3 ( 30 συνθ + 16 ) συνθ = 20 - 1/3 ( 30 0 + 16 ) 0 = 20 Ν
όταν συνθ = - 0,8 τότε ημθ = 0,6
(1) => FAx = Tx = Τ ημθ = ( 30 συνθ + 16 ) ημθ = ( 30 (-0,8) + 16 ) 0,6 = ( - 24 + 16 ) 0,6 = - 4,8 Ν
FE = 40 + 4/3 ( 30 συνθ + 16 ) συνθ = 40 + 4/3 ( 30 (-0,8) + 16 ) (-0,8) = 40 + 4/3 ( - 24 + 16 ) (-0,8) =
= 40 + 4/3 ( - 8) (-0,8) = 40 + 25,6/3 = 145,6/3 Ν
FΑy = 20 - 1/3 ( 30 συνθ + 16 ) συνθ = 20 - 1/3 ( 30 (-0,8) + 16 ) (-0,8) = 20 - 1/3 ( - 24 + 16 ) (-0,8) =
= 20 - 1/3 ( - 8) (-0,8) = 20 - 6,4/3 = 53,6/3 Ν

.....................................................................................................................................
..................................................................................................................................
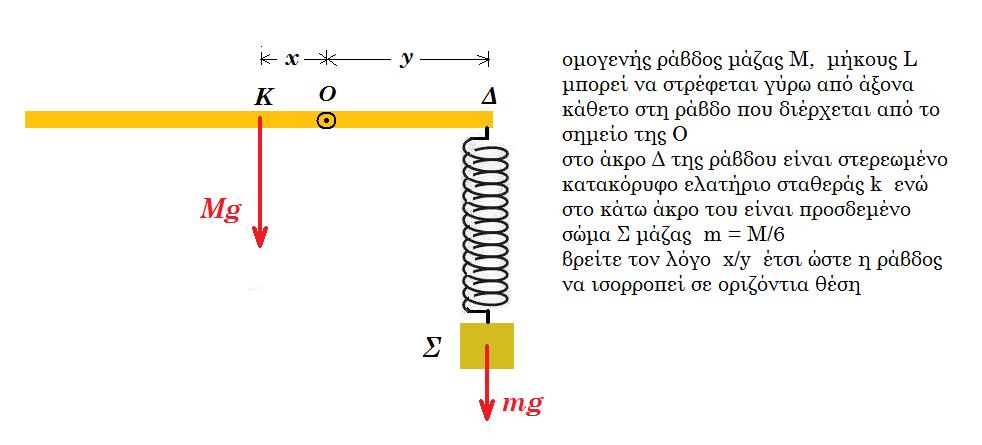
(AΔ) = 2 (ΔΓ) ημφ = 0,6 Μ = 3 m = 3 kg k = 100 N/m
..........................................................
 Η ομογενής δοκός ΑΒ του σχήματος, μήκους ℓ=3m και μάζας Μ=20kg ισορροπεί σε οριζόντια θέση, στηριζόμενη σε δύο στηρίγματα στα σημεία Κ και Λ, όπου (ΑΚ)=(ΚΛ)= (ΛΒ)=1m. Στο άκρο Α έχει στερεωθεί ιδανικό ελατήριο σταθεράς k=100Ν/m, στο πάνω άκρο του οποίου ισορροπεί σώμα Σ, μάζας m=4kg.
Η ομογενής δοκός ΑΒ του σχήματος, μήκους ℓ=3m και μάζας Μ=20kg ισορροπεί σε οριζόντια θέση, στηριζόμενη σε δύο στηρίγματα στα σημεία Κ και Λ, όπου (ΑΚ)=(ΚΛ)= (ΛΒ)=1m. Στο άκρο Α έχει στερεωθεί ιδανικό ελατήριο σταθεράς k=100Ν/m, στο πάνω άκρο του οποίου ισορροπεί σώμα Σ, μάζας m=4kg.







 Σωστή απάντηση είναι η
Σωστή απάντηση είναι η 








