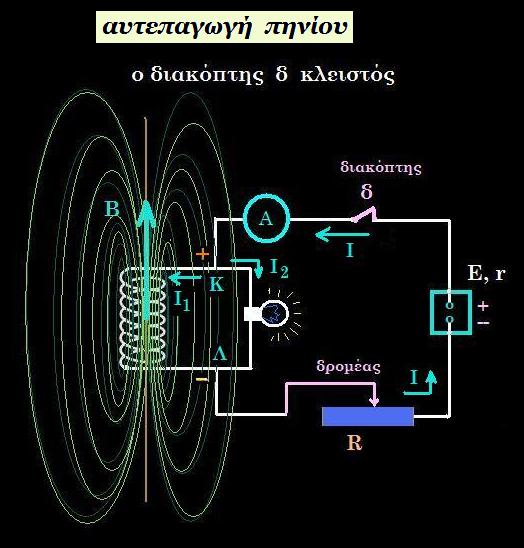
Mετακινούμε τον δρομέα του ροοστάτη από μια θέση (1)  R_ελαχ = R₀   σε άλλη θέση (2)  R_μεγ   σε χρονικό διάστημα  Δt,    τότε η ένταση του ρεύματος  Ι  μειώνεται  από μια μέγιστη τιμή  Ι_μεγ  σε μια ελάχιστη τιμή  Ι_ελαχ   σto χρονικό διάστημα  Δt,   οπότε το ρεύμα  Ι₁ = Ι_π  που διαρρέει το πηνίο  μειώνεται,    με συνέπεια  η ένταση του μαγνητικού πεδίου του πηνίου  να μειώνεται,   άρα  η μαγνητική ροή των δυναμικών γραμμών του πεδίου  να μειώνεται   σto χρονικό διάστημα  Δt.     Tο πηνίο αντιδρά στην μείωση  της μαγνητικής ροής   προσπαθώντας να την διατηρήσει σταθερή    αναπτύσσεται επαγωγική τάση στα άκρα  Κ, Λ   του πηνίου   Ε_επαγ = L dI_π/dt    

R = R₀ + β.t  (1)  β = ΔR/Δt  (2)    R_π,λ  = R_π R_λ / (R_π + R_λ)  (3)     Ι  =  Ι_λ  +  Ι_π   (4)    

   L dI_π/dt  +  Ι_π R_π  -  Ι_λ R_λ  =  0   =>     Ι_λ  =  L/R_λ  dI_π/dt  +  Ι_π R_π /R_λ   (5)

   Ε  -  L dI_π/dt  = Ι ( r + R ) +  Ι_π R_π  =>   Ε  -  L dI_π/dt  = Ι ( r + R₀ + β.t ) +  Ι_π R_π  (6)  

   Ε = Ι ( r + R ) +  Ι_λ R_λ    =>      Ε = Ι ( r + R₀ + β.t ) +  Ι_λ R_λ   (7)           

 R*  = ( R_π /R_λ + 1 ) ( r + R₀ + β.t ) + R_π  = ( 10/10 + 1 ) ( 5 + 10 + 10.t ) + 10  =  2 (15 + 10.t) + 10 = 40 + 20.t  

     A  =  1 + (r + R₀ + β.t)/R_λ =  1  + ( 5 + 10 + 10.t ) / 10  =  2,5 + t  

(6) =>   Ε  -  L dI_π/dt  = Ι ( r + R₀ + β.t ) +  Ι_π R_π   =>⁽⁴⁾   Ε  -  L dI_π/dt  = ( Ι_λ  +  Ι_π ) ( r + R₀ + β.t ) +  Ι_π R_π   

  =>   Ε  -  L dI_π/dt  = (  L/R_λ  dI_π/dt  +  Ι_π R_π /R_λ  +  Ι_π ) ( r + R₀ + β.t ) +  Ι_π R_π   =>  

  =>   Ε  =   L dI_π/dt  +  L(r + R₀ + β.t)/R_λ  dI_π/dt  +  Ι_π  { ( R_π /R_λ  + 1 ) ( r + R₀ + β.t ) + R_π }   =>  

  =>   Ε  =   L { 1 + (r + R₀ + β.t)/R_λ } dI_π/dt  +  Ι_π  { ( R_π /R_λ  + 1 ) ( r + R₀ + β.t ) + R_π }   =>  

  =>   Ε  =   L { 1 + (r + R₀)/R_λ } dI_π/dt  + β.t/R_λ  dI_π/dt  +  Ι_π  { ( R_π /R_λ  + 1 ) ( r + R₀ + β.t ) + R_π }   =>  *

  =>   30  =   0,1 { 1 + (5 + 10 + 10.t)/10 } dI_π/dt  +  Ι_π  { ( 10 / 10  + 1 ) ( 5 + 10 + 10.t ) + 10 }   =>  

  =>   30  =   0,1 { 1 + 1,5 + 1.t } dI_π/dt  +  Ι_π  { 2 ( 15 + 10.t ) + 10 }   =>  

  =>   - ( 0,25 + 0,1.t ) dI_π/dt  =  Ι_π ( 40 + 20.t ) - 30  =>   dI_π/dt  =  - { Ι_π ( 40 + 20.t ) - 30 } / ( 0,25 + 0,1.t ) =>

  =>   - ( 0,25 + 0,1.t ) dI_π  =  { Ι_π ( 40 + 20.t )  - 30 } dt  

* =>   Ε  =  AL dI_π/dt  +  Ι_π R*   =>   - AL dI_π/dt  =  Ι_π R* - Ε   =>  - AL dI_π/dt  = R* (Ι_π - Ε/R*)   =>    

  =>   dI_π/(Ι_π - Ε/R*)  =  - R*/AL  dt   =>    ln [ (Ι_π - Ε/R*) / (Ι_π - Ε/R*) ]  =  - R*/AL t     =>   Ι_π(t) =  Ε/R*  e^{- R*/AL t}    

  t = 0    R = R_ελαχ = 10 Ω     R* = ( R_π /R_λ + 1 ) ( r + R_ελαχ ) + R_π  =  ( 10 /10 + 1 ) ( 5 + 10 ) + 10  =  2  15 + 10  = 40 Ohm

    A  =  1 + ( r + R_ελαχ )/R_λ  =  1  +  ( 5 + 10 ) / 10  =  1 + 1,5 = 2,5  

    Ι_π(0) =  Ε/R*  e^{- R*/AL t}    =  30/40  e⁰    =  0,75 A      I_λ(0)  =  0,75 Α       Ι = 1,5 Α  

  t > 0    R = R_μεγ = 95 Ω    R* = ( R_π /R_λ + 1 ) ( r + R_μεγ ) + R_π  =  ( 10 /10 + 1 ) ( 5 + 95 ) + 10  =  2  100 + 10  = 210 Ohm

    A  =  1 + ( r + R_μεγ )/R_λ  =  1  +  ( 5 + 95 ) / 10  =  1 + 10 =  11  

    Ι_π(t) =  Ε/R*  e^{- R*/AL t}    =  20/210  e^{- 210 / (11 0,1) 0,01}   =  0,1 A      I_λ(0)  =  0,1 Α       Ι = 0,2 Α