Το παραπάνω σύστημα στρέφεται περί κατακόρυφο άξονα που περνά από ένα τυχαίο σημείο Ο της ράβδου με σταθερή γωνιακή ταχύτητα μέτρου ω και φοράς αντίθετης της φοράς του ρολογιού, όπως φαίνεται στο σχήμα 2.

Screenshot-2

 

γ) Να εκφράσετε τη στροφορμή του συστήματος ως προς τον άξονα που διέρχεται από το σημείο Ο.

δ) Να αποδείξετε ότι η ελάχιστη τιμή του μέτρου της στροφορμής του συστήματος είναι περί άξονα που διέρχεται από το κέντρο μάζας του.

  κεντρο μάζας Κ :   Στ(Ο) = 0  =>

 =>  m1 g r1  =  m2 g r2  =>  m1 r1 = m2 (d - r1)  =>  r1 = d m2 / (m1 + m2)       r2 = d m1 / (m1 + m2)   

  στροφορμή :  L  =  m1  ω x12  +  m2  ω x22  =  m1  ω x12  +  m2  ω  (d - x1)2  =>

   =>  L  =  m1  ω x12  +  m2  ω  d2  -   2 m2  ω d x1   +  m2  ω  x12  =>

   =>  (m1 + m2) ω x12  -   2 m2  ω d x1  +  m2  ω  d2  -  L  =  0 

  Δ  =  4 ω2 m22 d2  -  4 (m1 + m2) ω ( m2  ω  d2  -  L )  =  0  => 

        =>   4 ω2 m22 d2  =  4 (m1 + m2) ω ( m2  ω  d2  -  L )  =>  

       =>   4 ω2 m22 d2  =  4 (m1 + m2) ω  m2  ω  d2  -  L  4 (m1 + m2) ω  =>  

       =>  -  4 ω2 m22 d2  +  4 (m1 + m2) ω  m2  ω  d2  =  L  4 (m1 + m2) ω  =>  

       =>  -  4 ω2 m22 d2  +  4 m1 m2  ω2 d2  +  4 m22 ω2 d2  =  L  4 (m1 + m2) ω  =>  

       =>   4 m1 m2  ω2 d2  =  L  4 (m1 + m2) ω  =>  L  = ω d2 m1 m2 / (m1 + m2)    ω d2        ελάχιστη στροφορμή συστήματος  m1 , m2 

 

  x1  =  2 m2  ω d / 2 (m1 + m2) ω  =  d m2 / (m1 + m2)   

 

 

 

 

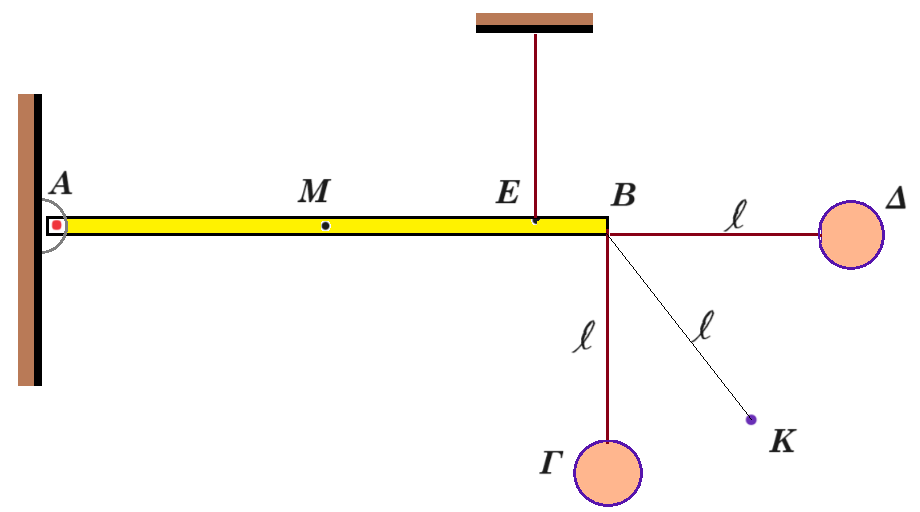
Λεπτή ομογενής ράβδος ΑΒ, μήκους 2m, βάρους w=24Ν ηρεμεί σε οριζόντια θέση, αρθρωμένη σε κατακόρυφο τοίχο στο άκρο της Α, ενώ είναι δεμένη στο άκρο κατακόρυφου μη εκτατού νήματος, στο σημείο Ε, όπου (ΕΒ)=0,2m. Μια σφαίρα μάζας 5kg κρέμεται μέσω αβαρούς νήματος,  μήκους  l=1m, από το άκρο Β  της ράβδου.

i)   Να υπολογισθεί η δύναμη που ασκείται στη ράβδο από την άρθρωση, στο άκρο της Α.

ii)  Εκτρέπουμε τη σφαίρα, φέρνοντάς την στη θέση Δ, όπου το νήμα είναι τεντωμένο (με μηδενική τάση) και οριζόντιο και την αφήνουμε να κινηθεί. Να υπολογισθεί η δύναμη που ασκείται στη ράβδο από την άρθρωση:

α)  Αμέσως μόλις αφεθεί η σφαίρα να κινηθεί στην θέση Δ.

β)  Τη στιγμή που η σφαίρα περνά από την θέση Γ.

iii)  Κατά την πτώση της σφαίρας, κάποια στιγμή πέρασε από μια θέση Κ, όπου ο ρυθμός μεταβολής της στροφορμής της (θεωρούμε την σφαίρα ως υλικό σημείο), ως προς το κέντρο Β της κυκλικής τροχιάς που διαγράφει, έχει μέτρο 24kg∙m2/s2. Για τη στιγμή αυτή ζητούνται:

α)  Η στροφορμή της σφαίρας ως προς το σημείο Β.

β)  Η δύναμη που ασκεί η άρθρωση στην ράβδο.

 

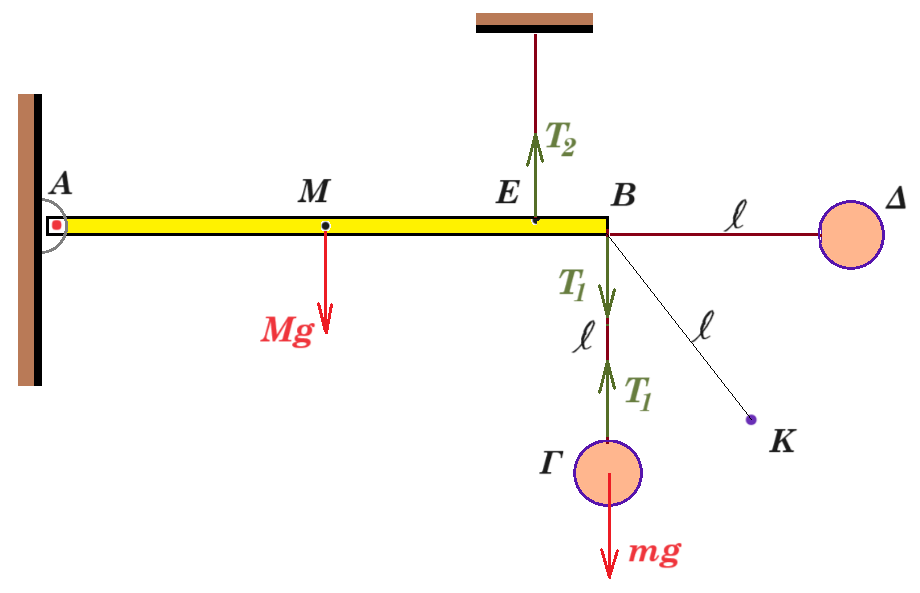
   ισορροπία σφαίρας :  T1  = mg = 50 N  

ισορροπία ράβδου :  Στ(Α) = 0  =>  Τ2 (ΑΕ)  -  Mg (AM)  -  T1 (AB)  =  0  =>  Τ2 1,8  -  24  1  -  50  2  =  0  =>  T2 = 124 / 1,8 = 620/9 N  

ΣFy = 0  =>  FA  +  T2  -  Mg  -  T1  =  0  =>  FA  +  620/9  -  24  -  50  =  0  =>  T2 = ( 74 9  -  620 ) / 9  =  46/9 N   

   

ισορροπία ράβδου :  Στ(Ε) = 0  =>   Mg (ΕM)  -  FA (ΑΕ)  =  0  =>  24  0,8  =  FA  1,8   =>  FA = 24 8 / 18 =  32/3 Ν       όταν η σφαίρα είναι στη θέση Δ  

 

διατήρηση ενέργειας για τη σφαίρα από θέση Δ  έως θέση Γ :    mg l  =  0,5 m vΓ2  =>  vΓ2 = 2gl = 2  10  1 = 20       

  η σφαίρα περνά από τη θέση Γ :  ΣFy = m vΓ2 / l  =>  T1  -  mg = m vΓ2 / l  =>  T1  -  50  =  5  20 / 1  =>  T1 = 50 + 100 = 150 N  

ισορροπία ράβδου :  Στ(Ε) = 0  =>   Mg (ΕM)  +  FA (ΑΕ)  -  T1 (EB)  =  0  =>  24  0,8  +  FA  1,8  -   150  0,2   =  0   =>  FA =  108 / 18 =   6 Ν   φορά προς τα κάτω       όταν η σφαίρα περνά από τη θέση Γ  

 

ρυθμός μεταβολής στροφορμής  =  συνισταμένη ροπών  

dL/dt  =  Στ(Β) =  mg x  =>  24  =  50  x  =>  x = 0,48 m    

 

 

Δυο σφαίρες περασμένες σε ράβδο

Οριζόντια αβαρής ράβδος μήκους 2D = 4 m είναι πακτωμένη στο μέσο της πάνω σε κατακόρυφο άξονα που στρέφεται με συχνότητα f = 5 Hz. Στη ράβδο έχουμε περάσει δύο σφαίρες που έχουν μάζες m1= m = 2 kg και m2 = 3m, οι οποίες έχουν οπή κατά μήκος μιας διαμέτρου ώστε να μπορούν να ολισθαίνουν χωρίς τριβές πάνω στη ράβδο. Οι σφαίρες συνδέονται με αβαρές νήμα μήκους D. Να υπολογίσετε:

i. τις αποστάσεις r1 και r2 των σφαιρών από τον άξονα.

ii. την ορμή του συστήματος των δύο σφαιρών.

iii. τη στροφορμή του συστήματος των δύο σφαιρών.

iv. την κινητική ενέργεια του συστήματος των δύο σφαιρών.

Κάποια στιγμή κόβεται το νήμα που συνδέει τις δύο σφαίρες που μετατοπίζονται και σταματούν στα άκρα της ράβδου, σε απόσταση D από τον άξονα η κάθε μία, όπου συγκρούονται πλαστικά με τα εμπόδια. Να υπολογίσετε:

ν. τη νέα γωνιακή ταχύτητα της ράβδου.

vi. την θερμότητα που ελευθερώθηκε.

Τ = Fκ = m1 ω2 r1 = m2 ω2 r2 =>   m  r1 = 3m  r2 =>   r1 = 3.r2     r1 + r2 = D => 4.r2 = 2 m => r2 = 0,5 m   r1 = 1,5 m

ptotal = m1 v1 - m2 v2 = m ω r1 - 3m ω r2 = m ω 3r2 - 3m ω r2 = 0

Ltotal = m ω r12 + 3m ω r22 = m ω 9r22 + 3m ω r22 = 12 m 2πf r22 = 12  2  2π 5  0,52  = 60.π kg.m2/s 

Ktotal = ½ m1 v12 + ½ m2 v22 = ½ m ω2 r12 + ½ 3m ω2 r22 = ½ m ω2 9r22 + ½ 3m ω2 r22 = 6 m ω2 r22  =

          = 6  2  102 π2  0,52  = 3000 J  

L = L'  => m ω r12 + 3m ω r22 = m ω' D2 + 3m ω' D2 =>   60.π kg.m2/s  = 4m ω' D2 => 60.π kg.m2/s  = 4  2 ω'  22 =>

            => ω'  = 60.π/32 kg.m2/s => ω'  = 15.π/8 kg.m2/s  

K ' =  ½ m (ω')2 D2 + ½ 3m (ω')2 D2 = 2 m (ω')2 D2 = 2  2  (15.π/8)2  22 =  2  2  ( 225.π2 / 64 )   22 =  2250 / 4 J    

 ΔΚ = Κ ' - Κ  =  2250/4  -  3000  = - 2437,5 J

 

 

 

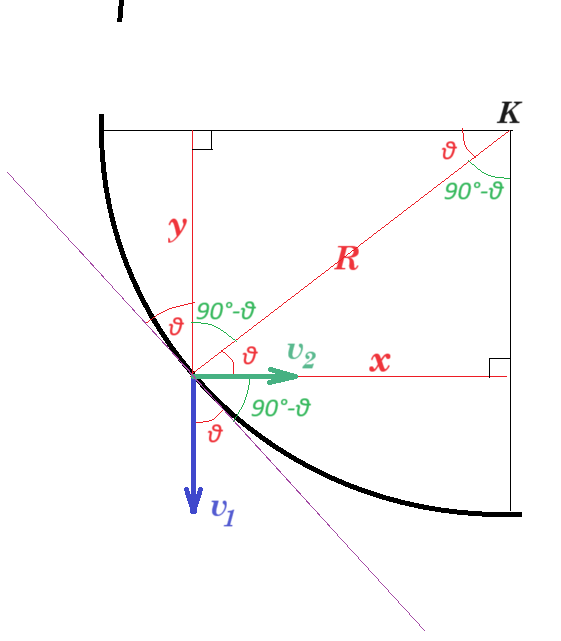
Ο λείος κατακόρυφος οδηγός (ΑΒ) της εικόνας, σχήματος τεταρτοκυκλίου κέντρου (Κ) και ακτίνας R είναι ακλόνητα στερεωμένος στο οριζόντιο επίπεδο.  Από σημείο της οριζόντιας ακτίνας (ΚΑ) του οδηγού που απέχει x από το κέντρο (Κ) αφήνουμε μικρό σώμα μάζας m.  Το σώμα αυτό αφού κινηθεί κατακόρυφα κατά y, συγκρούεται ακαριαία και πλάγια με σημείο του οδηγού. Αμέσως μετά την κρούση εκτελεί οριζόντια βολή φτάνοντας στη βάση (Β) του τεταρτοκυκλίου.  Το κλάσμα μεταβολής της κινητικής ενέργειας του σώματος λόγω της πλάγιας κρούσης είναι:
α) −𝟕/𝟏𝟔      β) −𝟏𝟔/𝟐𝟓       γ) 0

 

ελεύθερη πτώση :  y = ½ g t12     v1 = g t1       v12  =  2 g y    (1)

οριζόντια βολή :   R - y = ½ g t22      uy = g t2        ux = v2         x = v2 t2       

                            R - y =  g x2 / 2v22   =>  x / v2  =  [ 2(R - y)/g ]½     (2)        

διατήρηση στροφορμής ως προς Κ :    m v1 x  =  m v2 y  =>  x / v2 = y / v1    (3)

(2) , (3) =>  y / v1  =  [ 2(R - y)/g ]½   =>(1)   y / (2gy)½  =  [ 2(R - y)/g ]½  =>  ( y/2g )½  =  [ 2(R - y)/g ]½  =>  

          =>   y/2g  =  2(R - y)/g   =>  y/2  =  2(R - y)   =>  y  =  4R - 4y   =>  5y = 4R  =>  y = 0,8.R   

       x2  +  y2  =  R2  =>   x2  +  ( 0,8.R )2  =  R2   =>  x2  =  ( 0,6.R )2  =>  x = 0,6.R     

   (3) =>  x / v2 = y / v1  =>  0,6.R / v2  =  0,8.R / v1   =>  v1 / v2 = 8/6 = 4/3   

   K1 =  ½ m v12         K2 =  ½ m v22         dK =  K2 - K1  =   ½ m ( v22  -  v12 )         

   dK / K1 =   ½ m ( v22  -  v12 )  /  ½ m v12   =  ( v2 / v1 )2 - 1 =  ( 3/4 )2  -  1  =  9/16 - 1 =  - 7/16  

 
 
 

 

Μια μικρή σφαίρα μάζας m=2kg, την οποία θεωρούμε υλικό σημείο, περιστρέφεται πάνω σε λείο οριζόντιο τραπέζι, δεμένη στο ένα άκρο αβαρούς νήματος μήκους l=1,5m, με ταχύτητα σταθερού μέτρου υο=3m/s. Η παραπάνω περιστροφή επιτυγχάνεται, αφού το νήμα περνά από μια τρύπα Ο, στην επιφάνεια του τραπεζιού και στο άλλο του άκρο Α, ασκούμε μια κατακόρυφη δύναμη F, μέτρου Fο =22,5Ν, όπως στο σχήμα. Κάποια στιγμή t=0, αυξάνουμε το μέτρο της δύναμης F, (καθιστώντας την μεταβλητή), οπότε μετά από λίγο τη στιγμή t1, το άκρο Α του νήματος έχει κατέβει κατά h=0,2m έχοντας ταχύτητα υΑ=0,1m/s, ενώ η δύναμη έχει μέτρο F1=60Ν.

(1)   Ποιο το αρχικό μήκος του κατακόρυφου τμήματος (ΟΑ) του νήματος;

(2)   Να υπολογιστεί η στροφορμή και ο ρυθμός μεταβολής της στροφορμής της σφαίρας, ως προς το σημείο Ο, την στιγμή t1.

(3)   Να υπολογιστεί το έργο της μεταβλητής δύναμης F, μέχρι τη στιγμή t1.

(4)   Για την στιγμή t1 να βρεθούν ακόμη:

    4α)  Η κινητική ενέργεια και ο ρυθμός μεταβολής της κινητικής ενέργειας της σφαίρας.

    4β)  Η επιτάχυνση του άκρου Α του νήματος.

Δίνεται ότι η στροφορμή ενός υλικού σημείου το οποίο κινείται με ταχύτητα υ στο επίπεδο της σελίδας, ως προς ένα σημείο Ο του επιπέδου, είναι κάθετη στο επίπεδο, όπως στο σχήμα και έχει μέτρο L=mυ1r, όπου υ1 η συνιστώσα της ταχύτητας η κάθετη στην απόσταση r.

 

 

 

 

 

Το ελατήριο του σχήματος είναι ιδανικό έχει σταθερά k και φυσικό μήκος L0 = 1 m. Το σώμα που θεωρείται υλικό σημείο έχει μάζα m = 1 kg και είναι δεμένο στο ένα άκρο του ελατηρίου το άλλο άκρο του οποίου είναι κατάλληλα συνδεδεμένο με κατακόρυφο λείο άξονα. Το σύστημα βρίσκεται πάνω σε λείο οριζόντιο δάπεδο και περιστρέφεται με σταθερή γωνιακή ταχύτητα μέτρου ω0 = 7,5 rad/s με το ελατήριο να συγκρατείται στο φυσικό του μήκος με τη βοήθεια του νήματος που είναι δεμένο με το ένα άκρο στο σώμα και με το άλλο του άκρο στον άξονα. Κάποια στιγμή το νήμα σπάει, αν η μέγιστη παραμόρφωση του ελατηρίου είναι x0 = 0,5 m τότε η σταθερά του ελατηρίου είναι:       α. 125 N/m                    β. 225 N/m                γ. 100 N/m

 

  m ω0 L02  =   m ω ( L0 + x0 )2  =>  1  7,5  12  =   1  ω ( 1 + 0,5 )2  =>  ω = 7,5 / 2,25 = 10/3 rad/s  

  ½ m ω02 L02  =    ½ m ω2 ( L0 + x0 )2  +   ½ k x02   =>   1 7,52  12  =   1  (10/3)2  1,52  +   k  0,52   =>     

 =>   225/4   =   100/9  9/4   +   k  1/4   =>   k = 125 N/m         

 

 

 

 

Δυο  μικρές σφαίρες Α και Β, αμελητέων διαστάσεων, είναι δεμένες στα κάτω άκρα δύο αβαρών και μη εκτατών νημάτων, με το ίδιο μήκος l=2m,  τα άλλα άκρα των οποίων έχουν δεθεί σε σταθερό σημείο Ο. Εκτρέπουμε την σφαίρα Α κατά γωνία θ (όπου ημθ=0,8 και συνθ=0,6) και την σφαίρα Β στην αντίθετη πλευρά, ώστε το νήμα να γίνει οριζόντιο, όπως στο σχήμα. Σε μια στιγμή αφήνουμε ελεύθερη την σφαίρα Β και μετά από λίγο και την σφαίρα Α. Οι δυο σφαίρες συγκρούονται στην θέση Κ, όπου τα νήματα γίνονται κατακόρυφα. Η Α σφαίρα έχει μάζα 0,4kg και μετά την κρούση κινείται προς τα αριστερά, με αποτέλεσμα το νήμα εκτρέπεται κατά μια μέγιστη γωνία φ, όπου συνφ=0,75. Ζητούνται:

  1. Ο αρχικός ρυθμός μεταβολής της στροφορμής της σφαίρας Α, αμέσως μόλις αφεθεί να κινηθεί, ως προς το σημείο Ο.
  2. Η στροφορμή της σφαίρας Α και ο ρυθμός μεταβολής της, ως προς το Ο, ελάχιστα πριν την κρούση των δύο σφαιρών.
  3. Το μέγιστο μέτρο του ρυθμού μεταβολής της στροφορμής της σφαίρας Α, ως προς το Ο, μετά την κρούση.
  4. Η μεταβολή της στροφορμής ως προς το Ο της σφαίρας Β, η οποία οφείλεται στην κρούση

 

 

  dL/dt = Στ(Ο) =  mg l ημθ = 0,4 10 2 0,8 = 6,4 N.m 

mg (l - l.συνθ) = ½ m vA2  =>  2gl (1 - συνθ) =  vA2  =>  vA2  =  2 10 2 (1 - 0,6) = 16  =>  vA = 4 m/s     

LA = m vA l = 0,4 4 2 = 3,2 kg.m2/s          dL/dt = Στ(Ο) =  mg l ημ0° = 0 N.m 

  dL/dt = Στ(Ο) =  mg l ημφ = 0,4 10 2  √7/4 =  2√7 N.m       

 mg (l - l.συνφ) = ½ m (vA')2  =>  0,4 10 2 (1 - 0,75) = ½ 0,4 (vA')2  =>  2 = 0,2 (vA')2  =>  υΑ' = √10 m/s

mg l = ½ m vΒ2  =>  2gl =  vΒ2  =>  vΒ2  =  2 10 2 = √40  =>  vΒ = 2√10 m/s   

mA vA + mB vB =   mA vA' + mB vB'  =>  

 ΔL = Lμετά - Lπριν =  mΒ l ( υμετά - υπριν )  =  l  ( mA vA  -  mA vA' )  = 

                                                                 = 2  0,4  ( 4  - (- √10 ) )  =  0,8 ( 4 + √10 )  

 

 

 

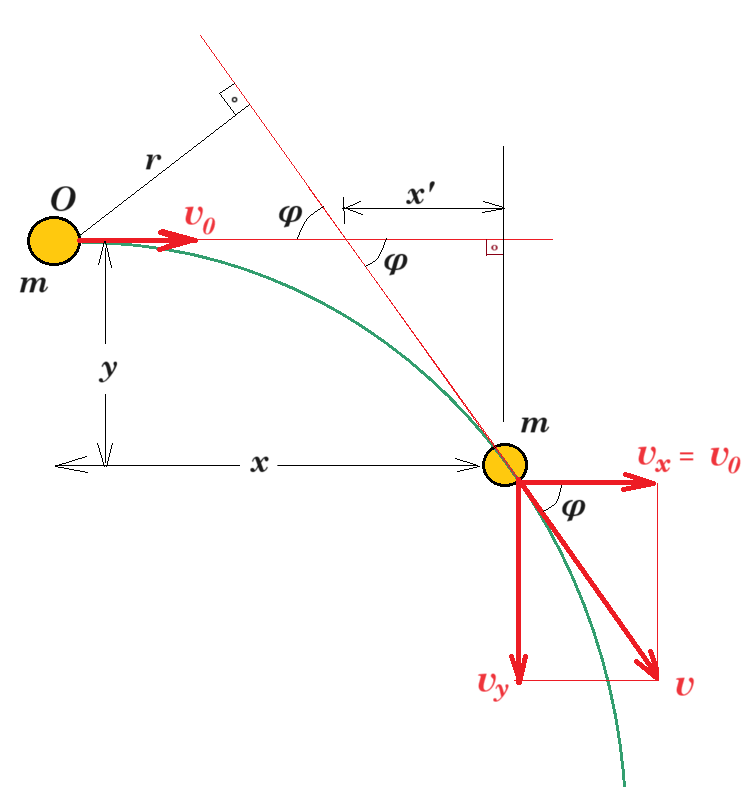
Μικρό σώμα μάζας m εκτελεί τη χρονική στιγμή t0 = 0, οριζόντια βολή στο κενό με αρχική ταχύτητα υ0.

1. Το μέτρο της στροφορμής L του υλικού σημείου ως προς τον άξονα που είναι κάθετος στο επίπεδο της τροχιάς και διέρχεται από το σημείο βολής (0) μεταβάλλεται με το χρόνο t σύμφωνα με τη σχέση:

α.  L = mgυ0t2/2                       β.  L = mgυ0t2                   γ.  L = 2mgυ0t2

2. Η απόσταση r του φορέα της ταχύτητας υ του σώματος από το σημείο βολής είναι ίση με:

α.  r = x∙ημφ                              β.  r = (x2 +y2)1/2 ∙εφφ              γ.  r = y∙συνφ

όπου x η οριζόντια και y η κατακόρυφη μετατόπιση του σώματος.

 

  x = v0 t   (1)          y = ½ g t2   (2)            vx = v0     (3)            vy = g t    (4)

  εφφ = vy / v0 = gt / v0    (5)                εφφ =  y / x' (6)

  gt / v0  = ½ g t2 / x'  =>  1 / v0  = ½ t / x'  =>  v0 t = 2x'  =>  x = 2x' =>  x' = x/2    (7)      

   ημφ = r / (x - x')  =>(7)  r  =  ημφ  x/2  =(7)  ημφ  x'  =(6)  συνφ  y 

στροφορμή ως προς το Ο :   L = m r v =  m r  (v02 + g2t2)½        (8)

στροφορμή ως προς το Ο :  L =  m y vx  -  m x vy  =  m ½gt2 v0  -  m  v0 t  g t  =  - mg v0 t2 / 2   (9)

 

 

 

 

 

 

 

Ένα υλικό σημείο αμελητέων διαστάσεων, με μάζα m=1kg, ηρεμεί σε λείο οριζόντιο επίπεδο δεμένο στο άκρο αβαρούς και μη εκτατού νήματος μήκους l=2m, το άλλο άκρο του οποίου έχει δεθεί σε σταθερό σημείο Ο. Σε μια στιγμή t=0, στο σώμα ασκούνται δύο οριζόντιες, σταθερού μέτρου δυνάμεις F1=F2=1Ν, όπου η F1 είναι κάθετη στο νήμα, ενώ η F2 σχηματίζει γωνία θ, με την προέκταση του νήματος, με αποτέλεσμα το σώμα να διαγράφει οριζόντιο κύκλο, όπως στο σχήμα (σε κάτοψη). Στο διπλανό διάγραμμα δίνεται η στροφορμή του σώματος, ως προς το κέντρο Ο της κυκλικής τροχιάς, σε συνάρτηση με το χρόνο, όπου τη στιγμή t΄=10s, παύει να ασκείται η δύναμη F1.

i)   Να υπολογιστεί ο ρυθμός μεταβολής της στροφορμής του σώματος, ως προς το Ο, τη χρονική στιγμή t1=5s.

ii)  Να βρεθεί η γωνία θ.

iii) Για την χρονική στιγμή t1=5s να υπολογιστούν:

α) Η ισχύς κάθε δύναμης που ασκείται  στο σώμα.

β) Η τάση  του νήματος.

γ) Η γωνιακή επιτάχυνση του σώματος.

iv) Να υπολογιστεί η στροφορμή του σώματος, ως προς το Ο, την χρονική στιγμή t2=14s.

i)        dL/dt =  8 kg m2/s / 10 s = 0,8 kg m2/s2            0  £  t  £ 10 s

ii)   0 £  t £ 10 s     dL/dt  =  Στ(Ο)  =  F1 l  -  F2 ημθ l  =>  0,8 kg m2/s2  =  1 N 2 m  -  1 N ημθ 2 m  => ημθ = 0,6

iii)      t = 5 s      L =  0,8 t    =>  L = 0,8  5  =  +4 kg m2/s  

      L = m v l  =>  4 kg m2/s  =   1 kg  v  2 m  =>  v = 2 m/s       

    PF1  =  F1 v  =  1 N  2 m/s = 2 J/s              

    PF2  =  F2 v  συν(π/2 + θ)  =  1 N  2 m/s  ( - ημθ )   = 1 N  2 m/s  ( - 0,6 ) =  - 1,2 J/s     

   ΣF = FK  =>  T - F2 συνθ   =  m v2/ l  =>  Τ  -  1 Ν 0,8  =  1 kg  (2 m/s)2 / 2 m  =>  Τ  =  2,8 N  

     ω = v / l = 2 m/s / 2 m = 1 rad/s        αγων  =  ω / t  =  1 rad/s / 5 s  =  0,2 rad/s2    

iv)   τη στιγμή t = 10 s  καταργείται η F1  και  στο σώμα ασκείσυν ται μόνο η F2        

           dL/dt  =  Στ(Ο)  =  - F2 ημθ l  = - 1 Ν 0,6  2 m  =  - 1,2 N.m

   L = - 1,2 t + b  =>   8 = - 1,2  10  + b  =>  b = 20 kg m2/s                   L = - 1,2 t + 20 

  t = 14 s   L =  - 1,2  14  +  20  =  + 3,2 kg m2/s  

 

 

 

Μικρό σφαιρίδιο μάζας m έχει περαστεί σε μια λεπτή αβαρή οριζόντια ράβδο ΟΑ η οποία μπορεί να στρέφεται χωρίς τριβές γύρω από τον κατακόρυφο σταθερό άξονα z′z, που διέρχεται από το άκρο Ο. Η ράβδος είναι λεία, έχει μήκος ℓ και στρέφεται με σταθερή γωνιακή ταχύτητα ω0. Το σφαιρίδιο εκτελεί ομαλή κυκλική κίνηση κέντρου Ο χάρη στο τεντωμένο αβαρές και μη εκτατό νήμα μήκους x = 3ℓ/5 που είναι δεμένο στο σφαιρίδιο και στον άξονα z′z, όπως φαίνεται στο σχήμα.

Κάποια στιγμή κόβουμε το νήμα οπότε το σφαιρίδιο φτάνει μετά χρόνο Δt στο άκρο Α της ράβδου όπου συγκρούεται και τελικά σταθεροποιείται σε αυτό.

  1. Ο χρόνος Δt είναι ίσος με:

α. 5/3ω0                                      β. 4/3ω0                       β. 5/4ω0

  1. Το μέτρο της γωνιακής ταχύτητας ω του σφαιριδίου μετά την σταθεροποίησή του στο άκρο της ράβδου είναι:

α. 9ω0/25                     β. 16ω0/25                   γ. 9ω0/16

  1. Το ποσοστό % μεταβολής της κινητικής ενέργειας του σφαιριδίου λόγω της σύγκρουσης με το άκρο της ράβδου είναι:

α. –36%                      β. –64%                      γ. –75%

 

στροφορμή του σώματος Σ :      L = m v r = m ω r r = m ω r2 

διατήρηση στροφορμής :     Lπριν = Lμετά  =>  m r2 ω0  =  m l2 ω  =>  (3l/5)2  ω0  =  l2  ω  =>  9/25 ω0  =  ω    

 

κινητική ενέργεια του σώματος Σ :     Κ = ½ m v2 = ½ m (ω r)2 =  ½ m ω2 r2        

μεταβολή της κινητικής ενέργειας του σώματος Σ :   ΔΚ = Κτελ - Καρχ =  ½ m ω2 l2   -  ½ m ω02 r2  =  

      =  ½ m  (9/25 ω0)2  l2   -  ½ m ω02 (3l/5)2  =  ½ m  ( 81/625  -  9/25 ) ω02  l2   =   - 144/625  ½ m  ω02  l2  

    ΔΚ / Καρχ =  ( - 144/625  ½ m  ω02  l2 )  /  ( ½ m ω02 (3l/5)2 )  =  - 16/25           - 64 %

 

 

 

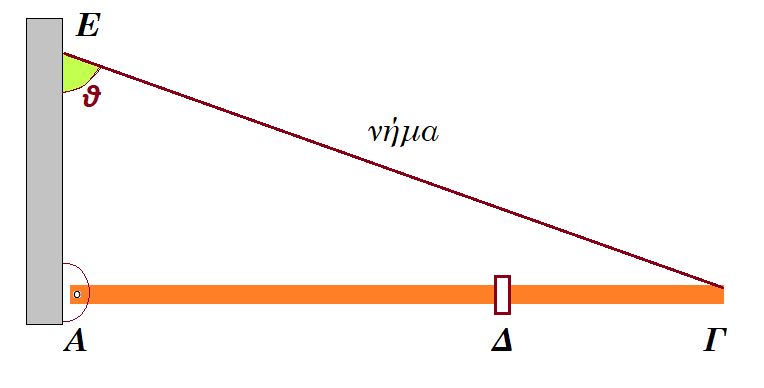Σώμα μικρών διαστάσεων μάζας  𝑚=3𝑘𝑔  είναι στερεωμένο πάνω σε ομογενή ράβδο ΑΓ μήκους 𝐿=3𝑚 και μάζας 𝑀=6𝑘𝑔.  Το σώμα βρίσκεται στη θέση Δ, η οποία απέχει απόσταση 𝛥𝛤=L/3  από το άκρο Γ της ράβδου.  Η ράβδος στηρίζεται με το άκρο της Α σε κατακόρυφο τοίχο μέσω άρθρωσης.  Η ράβδος ισορροπεί σε οριζόντια θέση με τη βοήθεια αβαρούς νήματος, το οποίο συνδέει το άκρο Γ με τον κατακόρυφο τοίχο στο σημείο Ε, όπως φαίνεται στο σχήμα.  (ημθ=0,8  συνθ=0,6)  Το σύστημα ράβδος – σώμα μπορεί να περιστρέφεται ως προς άξονα ο οποίος διέρχεται από το σημείο Α και είναι κάθετος στη ράβδο και στο επίπεδο της σελίδας.  Η ροπή αδράνειας ομογενούς ράβδου μάζας Μ και μήκους L, ως προς άξονα περιστροφής που διέρχεται από το άκρο της και είναι κάθετος στη ράβδο δίνεται από τη σχέση I = 1/3 M L2 
(α)  Να υπολογίσετε τη ροπή αδράνειας του συστήματος ράβδος - σώμα, ως προς τον άξονα
περιστροφής που διέρχεται από το σημείο Α  και  την δύναμη που δέχεται η ράβδος στο σημείο Α.  

Κάποια χρονική στιγμή κόβουμε το νήμα και το σύστημα αρχίζει να περιστρέφεται, χωρίς τριβές, σε κατακόρυφο επίπεδο γύρω από τον άξονα περιστροφής.
(β)  Να υπολογίσετε την ταχύτητα του σώματος μάζας m τη στιγμή που το σύστημα ράβδος - σώμα διέρχεται για πρώτη φορά από την κατακόρυφη θέση.


συνολική ροπή αδράνειας :   I  =  1/3 M L2  +  m (2L/3)2  =  1/3 6 32  +  3 (2 3/3)2  =  18  +  12  =>  Ι  =  30 kg m2    

ΣFx = 0  =>  Fx = Tx  =  T ημθ  =  Τ  0,8    (1)

ΣFy = 0  =>  Fy  +  Ty  =  Mg  +  mg          (2)

ροπές ως προς Α :  Στ(Α) = 0  =>  Τy L  -  Mg L/2  -  mg 2L/3  =  0  =>  Τ συνθ L  -  Mg L/2  -  mg 2L/3  =  0  =>

     =>  Τ  0,6  3  -   60  3/2  -   30 2 3/3  =  0  =>   Τ  0,6  =  50  =>  Τ = 250/3 Ν     (3)

(1) , (3)  =>  Fx =  Τ  0,8  =  250/3  0,8  =>   Fx =  200/3 Ν

(2) , (3)  =>  Fy  +  Ty  =  Mg  +  mg   =>   Fy  +  50  =   60  +  30    =>   Fy  = 80 Ν 

F2  =  Fx2  +  Fy2  =  (200/3)2  +  802  =  40000/9  +  6400  =  (40000  +  57600 ) / 9  =  97600 / 9  =>

   =>   F  =  312,4 / 3 =  104,13 N   το μέτρο της δύναμης που ασκείται στη ράβδο στην άρθρωση  ( σημείο Α )

 

κόβεται το νήμα      διατήρηση ενέργειας :

m g 2L/3  +  M g L/2  =   ½ I ω2  =>  3  10 2 3/3  +  6 10  3/2  =   ½  30  ω2  =>  60 + 90 = 15 ω2  =>  ω = 10½ rad/s

η ταχύτητα της μάζας  m  είναι :   v =  ω  2L/3  =  10½  2 3/3 =>  v = 2 10½ m/s  κάθετη στη σελίδα προς τα μέσα

 

 

 

 

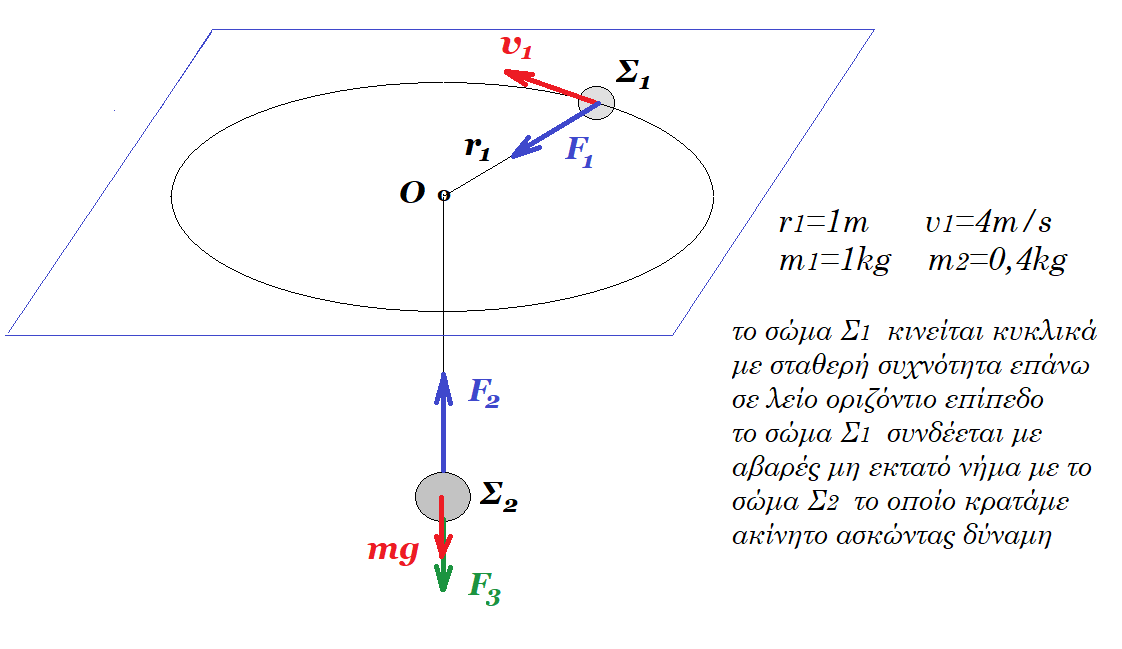
Το σφαιρίδιο Σ1 μάζας m1 = 1 kg κινείται πάνω στο λείο οριζόντιο τραπέζι εκτελώντας ομαλή κυκλική κίνηση ακτίνας r1 = 0,5 m δεμένο στο ένα άκρο Β του αβαρούς και μη εκτατού νήματος μεγάλου μήκους με υ1 = 4 m/s. Το νήμα περνά από λεία τρύπα του τραπεζιού και στο άλλο άκρο Α έχουμε δέσει σφαιρίδιο Σ2 μάζας m2 = 0,4 kg που το κρατάμε ώστε να παραμένει ακίνητο, με το νήμα να είναι κατακόρυφο και τεντωμένο. Δίνονται g = 10 m/s2, οι αντιστάσεις του αέρα αμελούνται και ότι οι διαστάσεις του τραπεζιού είναι μεγάλες.

α. Να βρεθεί η δύναμη  που ασκούμε στο σφαιρίδιο Σ2

Μετακινούμε το σφαιρίδιο Σ2 κατακόρυφα, αργά – αργά, ώστε το νήμα να παραμένει τεντωμένο, κατά d από την αρχική του θέση και αφήνουμε ελεύθερο το σφαιρίδιο Σ2. Παρατηρούμε ότι το σφαιρίδιο Σ2 παραμένει ακίνητο.

β. Να βρεθεί η μετατόπιση d

γ. Να βρεθεί το έργο της δύναμης που ασκούμε στο σφαιρίδιο Σ2 κατά την μετατόπιση του, d.

     

  f1 = ω1 / 2π = v1 / 2πr1  =  4m/s / (2π 0,5m)  =>  f1 = 4/π Hz   αρχική συχνότητα περιστροφής του σώματος Σ1 

 F1 = Fκ  =  m1 v12 / r1  =  1 kg  (4 m/s)2 / 0,5 m  =  32 N 

 F2 = F1  =  32 N      το νήμα είναι τεντωμένο 

 w2  =  m2 g  =  0,4 kg  10 m/s2  =  4 N  

για να διατηρήσουμε ακίνητο το σώμα Σ2  πρέπει να ασκήσουμε δύναμη  F3 = 32 - 4 = 28 Ν  ομόρροπη του βάρους του 

 

στη νέα θέση :   Τ =  m1 v22 / r2     και   Τ =   w2  =  m2 g  =  4 Ν     

συνεπώς  m1 v22 / r2  =  4 Ν  =>  1 kg  v22 / r2  =  4 Ν   =>  v22 / r2  =  4   (1)

 τα σώματα μετατοπίζονται κατά  d,   τότε  r2 = r1 + d  =  0,5  +  d   

στο σώμα Σ1  ασκούνται  στο κατακόρυφο άξονα  το βάρος του  w1  =  m1 g  και η αντίδραση  Ν από το λείο οριζόντιο επίπεδο οι οποίες είναι αντίθετες  και η συνισταμένη ροπή τους ως προς το σημείο Ο  ισούται με μηδέν, 

επίσης ασκείται η τάση του νήματος Τ  η οποία διέρχεται από το σημείο Ο  οπότε η ροπή της ως προς το σημείο Ο  ισούται με μηδέν 

  συνεπώς έχουμε διατήρηση στροφορμής   dL/dt = Στ(Ο) = 0  =>  dL = 0  => Lπριν = Lμετά  =>

         =>   m1 v1 r1  =  m1 v2 r2   =>  1  4  0,5 = 1  v2  r2   =>  2 =  v2 r2     (2)  

 (1) * (2)  =>   v23 = 8  =>  v2 = 2 m/s        (2) =>  r2 = 1 m       άρα η μετατόπιση είναι d = 0,5 m  το σώμα Σ1  απομακρύνεται  κατά  0,5 m   και  το σώμα Σ2  ανυψώνεται  κατά  0,5 m 

 

 διατήρηση ενέργειας :   m2 g d  +  0,5 m1 v22  =  0,5 m1 v12  +  W   =>   0,4  10  0,5  +  0,5 1   22  =  0,5  1  42  +  W   =>  2  +  2  =  8 +  W   =>   W = - 4 J   καταναλώσαμε ενέργεια  W = - 4 J   για να ανυψωθεί το σώμα Σ2  και στη νέα θέση να παραμένει ακίνητο   και  το σώμα Σ1  να απομακρυνθεί και στη νέα θέση να κινείται κυκλικά με σταθερή συχνότητα  f2 = ω2 / 2π = v2 / 2πr2  =  2m/s / (2π 1m)  =>  f2 = 1/π Hz  

 

 

 


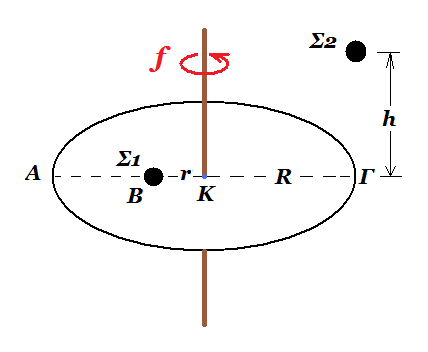
Οριζόντιος  δίσκος  αμελητέας μάζας  έχει ακτίνα  R = 0,3 m  και στρέφεται με σταθερή γωνιακή ταχύτητα  ω = 10π rad/s    γύρω από σταθερό κατακόρυφο άξονα που διέρχεται από το κέντρο του  (αμελητέες τριβές).   Επάνω στον δίσκο είναι στερεωμένο σφαιρίδιο Σ1  μάζας  m1 =  0,1 kg  στο σημείο Β  που απέχει απόσταση  r = 0,1 m  από το κέντρο του Κ.   Σε ύψος h   από τον δίσκο και σε απόσταση  R  από τον άξονα περιστροφής συγκρατούμε ακίνητο δεύτερο σφαιρίδιο Σ2  μάζας m1 = m2  =  0,1 kg .   Την στιγμή  t = 0  όπου η ακτίνα  ΚΒΑ είναι στο ίδιο κατακόρυφο επίπεδο με το σφαιρίδιο  Σ2  αφήνουμε αυτό ελεύθερο να κινηθεί.  Το σφαιρίδιο  Σ2  συγκρούεται πλαστικά με τον δίσκο   την στιγμή που αυτός έχει διαγράψει Ν = 2,5 περιστροφές.    

α)   Να υπολογισθεί το ύψος h.  

β)   Να υπολογισθεί η γωνιακή ταχύτητα του συστήματος  ( δίσκος - Σ1 - Σ2 ) μετά την κρούση.

 

N = 2,5 στροφές     θ = 2πΝ = 5π rad       θ  = ω t  =>  t  =  θ /ω  =  5π / 10π  =  0,5 s

  v1 =  ω r  =  10π rad/s  0,1 m  =  π m/s   

m2 g h = 0,5 m2 v22    =>  v22  =  2 g h        v2  =  g t  =  10 m/s2  0,5 s  =  5 m/s      h  =  0,5 g t2  =  0,5  10  0,52  =  5/4 m    

 

L  =  L'  =>   m1 v1 r   =  m1 ω r2  =  (m1 r2 + m2 R2 ) ω'  =>    0,1  10π  0,12  =  (0,1  0,12 + 0,1  0,32 ) ω'  =>   10π  0,01  =  ( 0,01 +   0,09 ) ω'   =>  π  0,1  =  0,1 ω'  =>   ω' = π rad/s

 

 

 

 

 

Ένα ποδήλατο του οποίου οι τροχοί έχουν ακτίνα R=0,2m, κινείται στην κατεύθυνση από το νότο προς το βορρά με ταχύτητα 6m/s. Ο ποδηλάτης φρενάρει και το σύστημα σταματά μετά από 3s. Σε όλη τη διάρκεια της ομαλά επιβραδυνόμενης κίνησης οι τροχοί κυλίονται.
α)  Να βρείτε πώς μεταβάλλεται η γωνιακή ταχύτητα των τροχών σε συνάρτηση με τον χρόνο και να τη σχεδιάσετε σε αριθμημένους άξονες.
β)  Να σχεδιάσετε έναν τροχό με το επίπεδό του κάθετο στο επίπεδο της σελίδας και πάνω του να σχεδιάσετε το διάνυσμα της γωνιακής επιτάχυνσης, καθώς και το διάνυσμα της αρχικής γωνιακής ταχύτητας.
γ)  Να γράψετε τη σχέση που συνδέει το μέτρο της στροφορμής ενός μικρού ανακλαστικού μάζας 10g, που είναι στερεωμένο στην περιφέρεια ενός τροχού του, σε συνάρτηση με τον χρόνο και να τη σχεδιάσετε σε αριθμημένους άξονες.
δ)  Να βρείτε τον αριθμό των περιστροφών που έκανε το ανακλαστικό μέχρι να σταματήσει το ποδήλατο.

    v  =  v0  -  a t   =>  0  =  6  -  a 3  =>  a  =  2 m/s2            αγων  =  α / R  =  2 / 0,2  =  10 rad/s2    

 v  =  ω R  =>   ω  =  v / R  =  ( v0  -  a t ) / R  =  ( 6  -  2 t ) / 0,2   =>  ω  =  30  -  10 t  

  L  =  m v R  =  m ω R2  =  0,01 kg  ( 30  -  10 t )  0,04 m2  =  ( 12 - 4.t ) 10-3 kg m2/s    

  θ = ω0 t  -  ½ αγων t2  =  30 3  -  ½  10  9  =  90  -  45  =  45 rad               N = θ / 2π  =  45 / 2π  περιστροφές

 

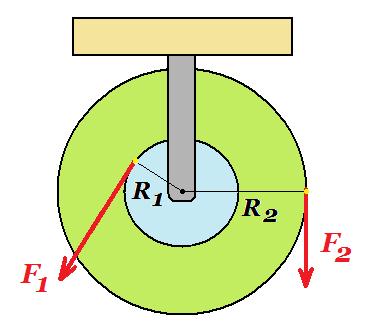
Η διπλή τροχαλία του σχήματος μπορεί να στρέφεται γύρω από σταθερό άξονα που συμπίπτει με τον άξονα συμμετρίας της.  Η τροχαλία έχει ακτίνες, R1=10cm, R2=20cm και είναι αρχικά ακίνητη.  Μέσω κατάλληλων αβαρών νημάτων ασκούνται στην τροχαλία οι δυνάμεις F1=60N και F2=40N, αντίστοιχα, με σημεία εφαρμογής και κατευθύνσεις, όπως δείχνονται στο σχήμα.  Η τροχαλία αποκτά γωνιακή επιτάχυνση ίση με αγων=2rad/s2.   Να υπολογίσετε:
α)  τη συνολική ροπή που δέχεται η τροχαλία.
β)  τη γωνιακή ταχύτητα της τροχαλίας τη χρονική στιγμή t=4s.
γ)  το μήκος του νήματος που έχει τυλιχτεί ή ξετυλιχτεί σε κάθε τροχαλία, τη χρονική στιγμή t=4s.
δ)  τη γωνία που διέγραψε η τροχαλία από τη χρονική στιγμή t1=2s μέχρι τη χρονική στιγμή t2=4s.
 
  Στ  =  F1 R1 - F2 R2  =  60 N 0,1 m  -  40 N 0,2 m  =  - 2 Nm  
    ω = αγων t  =  2 rad/s2  4 s  =  8 rad/s    
  l1  =  θ R1  =  ½  αγων t2  R1  =  ½  2 rad/s2  16 s2  0,1 m  = 1,6 m
  l2  =  θ R2  =  ½  αγων t2  R2  =  ½  2 rad/s2  16 s2  0,2 m  = 3,2 m
    Δθ =  ½ αγων t22  -  ½ αγων t12  =  ½  2 rad/s2  16 s2   - ½  2 rad/s2  4 s2    = =>  Δθ = 12 rad        
 
............................................................................................................................
 
Ένας δίσκος ακτίνας r=0,1m, που έχει κολλημένο στην περιφέρειά του ένα μικρό σώμα, μάζας m=10 g, μπορεί να περιστρέφεται γύρω από ακλόνητο άξονα, που διέρχεται από το κέντρο του και είναι κάθετος στο δίσκο.  Η μέγιστη ελκτική δύναμη μεταξύ του δίσκου και του σώματος είναι 6,4Ν.  Αρχικά ο δίσκος είναι ακίνητος.  Τη χρονική στιγμή t0=0s ασκείται στο δίσκο κατάλληλη δύναμη, με αποτέλεσμα ο δίσκος να αποκτήσει σταθερή γωνιακή επιτάχυνση μέτρου αγων=8rad/s2.   Να υπολογίσετε:
α)  το μέτρο της μεταβολής της γωνιακής ταχύτητας του δίσκου από τη χρονική στιγμή t1=2s μέχρι τη χρονική στιγμή t2=6s.
β)  τη γωνιακή ταχύτητα που πρέπει να αποκτήσει ο δίσκος για να αποσπαστεί το σώμα από την περιφέρεια του δίσκου.
γ)  τη στροφορμή του σώματος, τη στιγμή που αποσπάται.
δ)  το μήκος της τροχιάς που διέγραψε το σώμα μέχρι να αποσπαστεί.
 
 ω = αγων t   =>  Δω  =  αγων Δt  = 8rad/s2  ( 6s - 2s )  =  32 rad/s    
 Fκ  = m v2 / r  =>  6,4  =  0,01  υ2 / 0,1  =>  υ2  =  64  =>  υ = 8 m/s                    ω = υ/r  =  8 / 0,1  = 80 rad/s    
 L = m v r =  0,01  8  0,1  =  0,008 kg m2/s
  ω = αγων t  =>   t  = 80 rad/s / 8rad/s2  =  10 s         θ  =  ½  αγων t2  =  ½  8rad/s2  100 s2  =  400 rad  
  s  = r θ  =  0,1  400  =  40 m  
 
............................................................................................................................
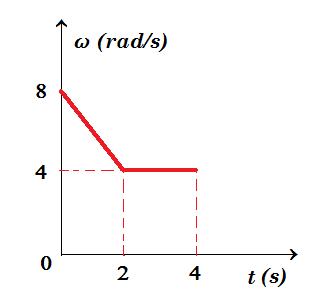
Ένας δίσκος ακτίνας R=0,1m, που έχει κολλημένο στην περιφέρειά του ένα μικρό σώμα μάζας m=10g, περιστρέφεται γύρω από ακλόνητο άξονα, που διέρχεται από το κέντρο του και είναι κάθετος στο δίσκο. Η γραφική παράσταση της γωνιακής ταχύτητας του δίσκου ως προς το χρόνο, δίνεται στο διάγραμμα.
Να υπολογίσετε:
α)  την αλγεβρική τιμή της γωνιακής επιτάχυνσης του δίσκου τις χρονικές στιγμές t1=1,5s και t2=2,5s.
β)  τον αριθμό των περιστροφών που εκτέλεσε ο δίσκος από τη χρονική στιγμή t3=1s μέχρι τη χρονική στιγμή t4=3s.
γ)  το μήκος της τροχιάς που έχει διαγράψει το σώμα στο χρονικό διάστημα από t3=1s μέχρι t4=3s.
δ)  το μέτρο της στροφορμής του σώματος ως προς τον άξονα περιστροφής του δίσκου τη χρονική στιγμή t4=3s.
 
α)   0 < t < 2s    aγων = Δω/Δt  =  (4 - 8) / (2 - 0) = - 2 rad/s2         2s < t < 4s     aγων = 0
β    ω  =  8 - 2t   0 < t < 2s         ω  =  4 rad/s   2s < t < 4s    
   t = 1s    ω  = 8 - 2 = 6 rad/s    όταν  1s < t < 2s    θ = (6 + 4)rad/s (2 - 1)s  / 2 =  5 rad  
                                               όταν  2s < t < 3s   ω  =  4 rad/s    θ =  4 rad/s (3 - 2)s  =  4 rad   
  από    1s  έως  3s     θ  =  5rad + 4 rad  =  9 rad               αριθμός περιστροφών :  Ν = θ / 2π = 9/2π 
γ)    s  =  R θ  =  0,1 m  9 rad  =  0,9 m
δ)   L = m v R = m ω R2  =  0,01 kg  4 rad/s  0,01 m2  =  4 .10-4 kg m2/s
 

............................................................................................................................

                στροφορμή ηλεκτρονίου

Fc  =  Fκ  =>    kc |qp qe|/ r2  = me v2 / r  =>   kc e e / r  = me v2   =>   kc e2 / 2r  = ½ me v2  = Κ

  U = - kc qp qe / r = - kc e2 / r                      E = K + U = - kc e2 / 2r   ολική ενέργεια ηλεκτρονίου

  στροφορμή ηλεκτρονίου   L = me v r    

   L2 =  me2 v2 r2  =  me2  ( kc.e2 / me.r )  r2  =  me kc e2 r  =>   L =  e ( kc me )½  r½      

 

              διπλός αστέρας  -  στροφορμή

FG = FK  =>  G m1 m2 / D2 =  m1 v12 / r1  =  m2 v22 / r2  =>  m1  ω2 r12 / r1  =  m2  ω2 r22 / r2  => 

              =>  m1 r1 =  m2 r2  =>   r2  =  m1 r1 / m2             

 r1 + r2 = D  =>   r1 + m1 r1 / m2  = D  =>  r1 ( 1 + m1 / m2 ) = D  =>  r1 = D m2 / (m1 + m2)  ,  r2 = D m1 / (m1 + m2)  

 

FG = FK  =>  G m1 m2 / D2 =  m1 v12 / r1  =>   G m2 / D2  = v12 / Dm2 /(m1 + m2)  =>   G m22 / D(m1 + m2) = v12   (1)  

L1 = m1 v1 r1  =  m1  m2 { G/D(m1 + m2) }½  Dm2 / (m1 + m2) =>   L1 =  m1 m22 { GD/(m1 + m2)3 }½   

FG = FK  =>  G m1 m2 / D2 =  m2 v22 / r2  =>   G m1 / D2  = v22 / Dm1 /(m1 + m2)  =>   G m12 / D(m1 + m2) = v22   (2) 

L2 = m2 v2 r2  =  m2  m1 { G/D(m1 + m2) }½  Dm1 / (m1 + m2) =>   L2 =  m2 m12 { GD/(m1 + m2)3 }½   

   από  (1) , (2)   εάν   m1 > m2   τότε   υ1 < υ2    και   L1 < L2          

 

   v1 =  2πr1 / Τ  =>   Τ = 2πr1 / v1   =   2π Dm2 /(m1 + m2)  / m2 { G/D(m1 + m2) }½   =>

                           =>  Τ  =  2π { D2/(m1 + m2)2  /  G/D(m1 + m2) }½   =>  Τ =  2π { D3 / G(m1 + m2) }½     

  ω = 2π / Τ = { G(m1 + m2) / D3 }½     

  L1 = m1 v1 r1  =  m1  ω  r12  =   m1  { G(m1 + m2) / D3 }½  D2 m22 / (m1 + m2)2  =

       =   m1 m22 { G(m1 + m2) / D3  D4 / (m1 + m2)4 }½  =   m1 m22 { GD / (m1 + m2)3 }½  

  L1 = m1 v1 r1  =  m1  ω  r12  

  L2 = m2 v2 r2  =  m2  ω  r22        L1 / L2 =  m1 / m2 . ( r1/ r2 )2  =   m1 / m2 . ( m2 / m1 )2  = m2 / m1   

 

............................................................................................................................

 

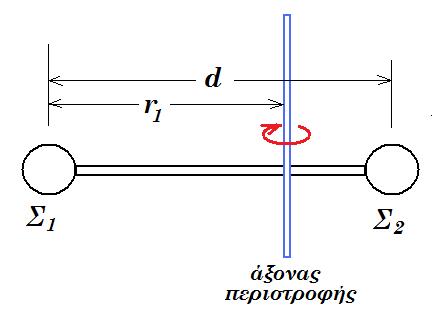
Δύο σημειακές σφαίρες Σ1 και Σ2 με μάζες m1=0,1kg και m2=0,4kg αντίστοιχα, συνδέονται μεταξύ τους με αβαρή ράβδο, όπως δείχνεται στο σχήμα. Οι σφαίρες απέχουν μεταξύ τους d=0,5m. Το σύστημα μπορεί να στρέφεται σε οριζόντιο επίπεδο γύρω από κατακόρυφο άξονα ο οποίος απέχει r1=0,4m από τη σφαίρα Σ1. Το σύστημα στρέφεται με σταθερή γωνιακή ταχύτητα, όπως οι δείκτες του ρολογιού και η σφαίρα Σ1 έχει στροφορμή L1=0,16kgm2/s. Να υπολογίσετε:
α) τη γραμμική ταχύτητα της σφαίρας Σ1.
β) τη γωνιακή ταχύτητα της σφαίρας Σ1.
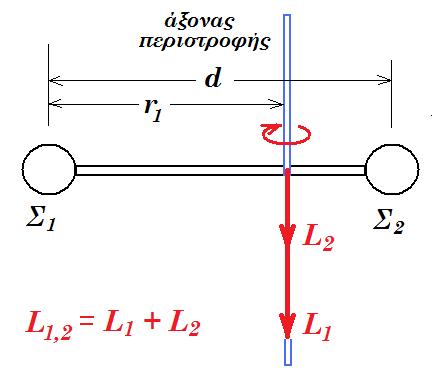
γ) τη στροφορμή της σφαίρας Σ2 και να τη σχεδιάσετε.
δ) τη συνολική στροφορμή του συστήματος.

 L1 = m1 v1 r1  =>   0,16kgm2/s  = 0,1kg  v1  0,4m  =>   v1  =  4 m/s              ω  = v1 / r1  = 4 m/s / 0,4 m  =  10 rad/s  

L2 = m2 v2  ( d - r1 )  =  m2  ω ( d - r1 )2  =  0,4 kg  10 rad/s ( 0,1 m )2  =  0,04 kg m2/s  

  L1,2  =  L1 + L2  =  0,16 + 0,04 = 0,2 kg m2/s  

 

...............................................................................................................................................................................

 

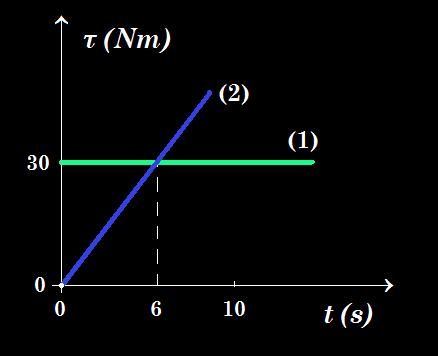
Υλικό σημείο που μπορεί να εκτελεί κυκλική κίνηση  διαγράφοντας οριζόντιο κύκλο σε λείο οριζόντιο επίπεδο  δέχεται μία δύναμη η ροπή της οποίας  ως προς το κέντρο του κύκλου μεταβάλλεται όπως το διάγραμμα (1)  ή  το διάγραμμα (2).  Πώς μεταβάλλεται η στροφορμή του υλικού σημείου συναρτήσει του χρόνου;    Πόση είναι η ροπή της δύναμης τη στιγμή  t = 10 s.   Πόση είναι η στροφορμή του την ίδια στιγμή;   Tην χρονική στιγμή t = 0  το υλικό σημείο έχει στοφορμή  L0 = 100 kg m2/s.  

 

 για το διάγραμμα (1) : ΔL / Δt  = τ  =  30 Νm  =>  L(t) = 30 t  + 100       L(10) = 30 10 + 100 = 400 kg m2/s           

 για το διάγραμμα (2) :  τ(t)  =  30/6 t  =  5 t        τ(6)  =  5 6  =  30 Nm           τ(10)  =  5 10  =  50 Nm  

                                   ΔL / Δt  = τ  =  30/6 t  =  5 t   =>  L(t) = 2,5 t2  + 100      L(10) = 2,5  102  + 100  =  350 kg m2/s     

 

...................................................................................................................

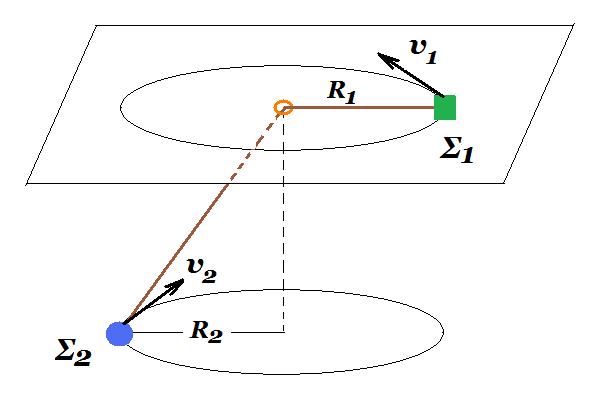
Σε λείο οριζόντιο επίπεδο (αμελητέου πάχους) σώμα Σ1 μάζας m1 = 0,8 kg  εκτελεί ομαλή κυκλική κίνηση ακτίνας R1 ενώ είναι δεμένο στο άκρο αβαρούς και μη εκτατού νήματος μήκους d.  Το νήμα περνά μέσα από πολύ μικρή οπή του οριζόντιου επιπέδου με την οποία δεν εμφανίζει τριβές και στο άλλο άκρο του είναι δεμένο σώμα Σ2 με μάζα m2 = 1 kg που εκτελεί επίσης ομαλή κυκλική κίνηση ίδιας ακτίνας με το Σ1 (R1 = R2 = 1,2 m).  Η συνολική στροφορμή του συστήματος των δυο σωμάτων ως προς άξονα κάθετο στο
οριζόντιο επίπεδο που διέρχεται από την οπή ισούται με μηδέν.  Θεωρήστε τα σώματα υλικά σημεία και τις αντιστάσεις από τον αέρα αμελητέες.  Δίνεται g = 10 m/s2.
Να υπολογίσετε :
1)  τα μέτρα των ταχυτήτων των δυο σωμάτων.
2)  το μέτρο της κεντρομόλου δύναμης που δέχεται το Σ1.
3)  το μήκος του νήματος.
4)  το μέτρο της στροφορμής του Σ2 ως προς άξονα κάθετο στο οριζόντιο επίπεδο που διέρχεται από τo Σ1 και την συνολική ορμή του συστήματος των δυο σωμάτων τη χρονική στιγμή t1 = 2π/45 s αν θεωρήσουμε ως t0 = 0 τη χρονική στιγμή που τα σώματα Σ1 και Σ2 βρίσκονταν στην ίδια κατακόρυφο.

 

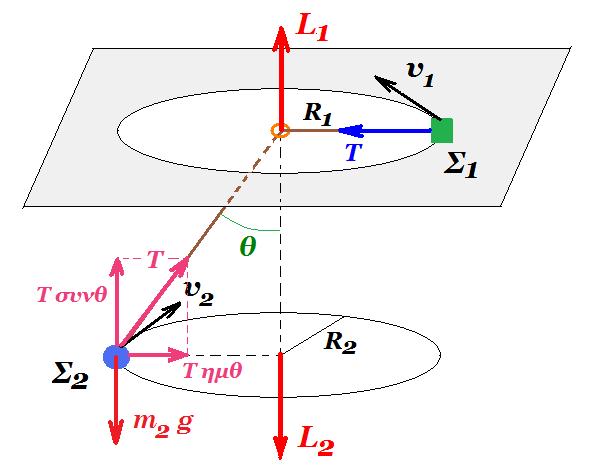
1) , 2)    m1 v1 R1  =  m2 v2 R2  =>   0,8  v1  1,2  =  1  v2  1,2  =>    v1 / v2  = 5/4  

  Τ  =  m1 v12 / R1     (1)

  Τ  ημθ  =    m2 v22 / R2    (2)         Τ συνθ  =  m2 g  =>   Τ συνθ  =  m2 g  =>  Τ 0,6  =  1 10  =>  Τ  =  10 / 0,6 = 100 / 6  =>  Τ = 50/3 Ν     

από  (1) , (2)  =>  m1 v12 / R1   =   m2 v22 / ( ημθ R2 )   =>  0,8  v12  =  1 v22 / ημθ  =>   v22 / ( 0,8 v12 ) =   ημθ  =>  16 / ( 25 0,8 )  =   ημθ   =>  ημθ = 20 / 25 = 0,8        τότε  συνθ = 0,6  

  η (1) =>   Τ  =  m1 v12 / R1   =>   50/3  =  0,8  v12 / 1,2   =>    v12  =  50  1,2  / ( 0,8 3 )  =  60 / 2,4  =  600 / 24  =  100 / 4  =  25  =>  v1  =  5 m/s      οπότε   v2  =  4 m/s  

3)   d  =  R1 +  R2 / ημθ   =  1,2  +  1,2 / 0,8  =  1,2  +  1,5  =  2,7 m   μήκος νήματος    

4)           L2  =  m2 v2 R2  =  1  4  1,2  =  4,8