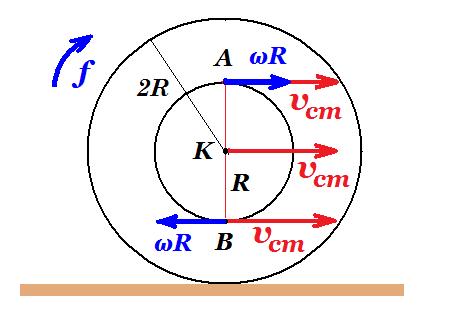
ο τροχός κυλίεται χωρίς να ολισθαίνει σε οριζόντιο επίπεδο με σταθερή γωνιακή ταχύτητα ω, ο λόγος των ταχυτήτων των σημείων Α και Β είναι : υΑ / υΒ = 1 ή 2 ή 3 ή 4 ;
ο τροχός κυλίεται χωρίς να ολισθαίνει σε οριζόντιο επίπεδο με σταθερή γωνιακή ταχύτητα ω, ο λόγος των ταχυτήτων των σημείων Α και Β είναι : υΑ / υΒ = 1 ή 2 ή 3 ή 4 ;
vcm = ω 2R vA = vcm + ω R = ω 2R + ω R = 3ωR vB = vcm - ω R = ω 2R - ω R = ωR υΑ / υΒ = 3
..........................................................................................
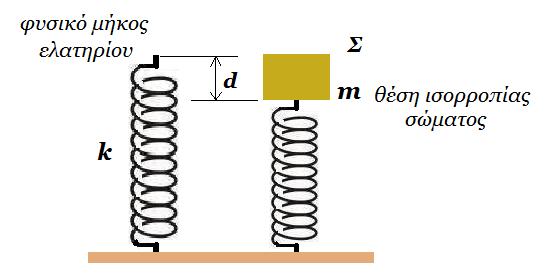
Μικρό σώμα Σ μάζας m ακουμπά στο άνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k και ισορροπεί, χωρίς να είναι συνδεδεμένο με αυτό, ενώ το ελατήριο είναι συσπειπωμένο κατά d. Συσπειρώνουμε επιπλέον το ελατήριο κατακόρυφα κατά 2d και τη χρονική στιγμή t0 = 0 αφήνουμε το σώμα ελεύθερο να κινηθεί. Το σώμα εκτελεί Α Α Τ σταθεράς D = k για όσο χρόνο είναι σε επαφή με το ελατήριο. Η αντίσταση του αέρα θεωρείται αμελητέα. Το διάστημα που διανύει το σώμα από τη χρονική στιγμή t0 = 0 μέχρι να μηδενισθεί η ταχύτητά του για πρώτη φορά ισούται με :
α) 4 d β) 4,25 d γ) 4,5 d
ισοροπία Σ : mg = kd x(t) = 2d ημ(ωt + π/2) v(t) = ω2d συν(ωt + π/2) θετική κατεύθυνση = κατακόρυφη προς τα κάτω
x(t) = 2d ημ(ωt + π/2) = - d => ημ(ωt + π/2) = - 1/2 συν(ωt + π/2) = - √3/2
το σώμα Σ ξεκινά την ταλαντωσή του την χρονική στιγμή t0 = 0 από την κάτω ακραία θέση και όταν φθάνει στη θέση x = - d χάνει την επαφή με το ελατήριο έχοντας διανύσει απόσταση 3d και έχοντας αποκτήσει ταχύτητα v1 = ω2d συν(ωt + π/2) = ω2d (- √3/2) = - √3 ωd επειδή κινείται κατακόρυφα προς τα πάνω
το σώμα Σ θα κάνει κατακόρυφη βολή προς τα πάνω
v = v1 - g t => 0 = v1 - g t => v1 = g t => t = v1 / g = √3 ωd / g
θα διανύσει απόσταση y = v1 t - ½ g t2 = √3 ωd (√3 ωd / g) - ½ g (√3 ωd / g)2 = 3 ω2 d2 / g - ½ g 3 ω2d2 / g2 =
= 3 ω2d2 / g - 3/2 ω2d2 / g = 3/2 ω2d2 / g = 3/2 k/m (mg / k)2 / g = 3/2 mg / k = 3/2 d
συνολικά το σώμα Σ θα διανύσει απόσταση : 3d + 3/2 d = 4,5 d
..........................................................................................
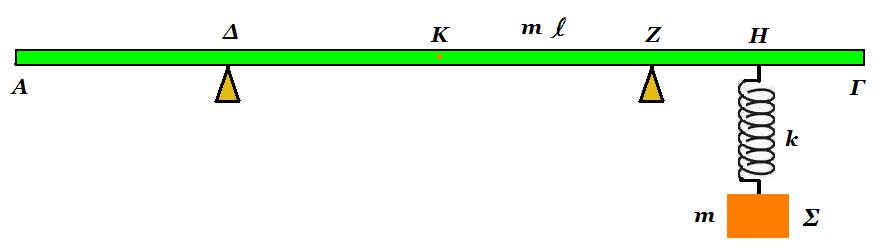
ΑΚ = ΚΓ = l /2 , ΑΔ = ΖΓ = l /4 , ΗΓ = l /8 . η δοκός ΑΓ και το σώμα Σ έχουν ίσες μάζες m ,
Δίνουμε στο σώμα Σ κατακόρυφη ταχύτητα μέτρου υ1 προς τα κάτω οπότε καθώς κατέρχεται εκτελώντας Α Α Τ σταθεράς D = k η δοκός οριακά δεν εκτρέπεται από την οριζόντια θέση.
Στη συνέχεια φέρνουμε ξανά το σώμα στη θέση ισορροπίας του όπου ισορροπεί. Δίνουμε στο σώμα Σ κατακόρυφη ταχύτητα μέτρου υ2 προς τα πάνω οπότε καθώς ανέρχεται εκτελώντας Α Α Τ σταθεράς D = k η δοκός οριακά δεν εκτρέπεται από την οριζόντια θέση. Ο λόγος υ1 / υ2 ισούται με :
α) 4/7 β) 5/7 γ) 6/7
θετική κατεύθυνση = κατακόρυφη προς τα κάτω
ισοροπία Σ : mg = Fελατ = kx0 |FΗ| = |Fελατ|
Α Α Τ σώματος Σ : k = mω2 υ1 = ωΑ1 x(t) = Α1 ημωt v(t) = ωΑ1 συνωt α(t) = - ω2 Α1 ημωt
ΣF = ma => Fελατ + mg = - mω2 Α1 ημωt => Fελατ = - mg - kΑ1 ημωt = - k ( x0 + x )
FΗ = - Fελατ = mg + kΑ1 ημωt = k ( x0 + x )
το μέγιστο μέτρο της δύναμης FΗ είναι το : k ( x0 + x ) = k ( x0 + Α1 ) = mg + kΑ1
οριακή ισορροπία δοκού ροπές ως προς Ζ : Στ(Ζ) = 0 => mg (ΚΖ) = |FΗ| (ΖΗ) =>
=> mg l/4 = ( mg + kΑ1 ) l/8 => 2mg = mg + kΑ1 => mg = kΑ1 => Α1 = mg / k = x0
υ1 = ωΑ1 => υ1 = ω mg / k = g/ω
θετική κατεύθυνση = κατακόρυφη προς τα πάνω
ισοροπία Σ : mg = Fελατ = kx0 |FΗ| = |Fελατ|
Α Α Τ σώματος Σ : k = mω2 υ2 = ωΑ2 x(t) = Α2 ημωt v(t) = ωΑ2 συνωt α(t) = - ω2 Α2 ημωt
ΣF = ma => Fελατ - mg = - mω2 Α2 ημωt => Fελατ = mg - kΑ2 ημωt = - k ( - x0 + x )
FΗ = - Fελατ = - mg + kΑ2 ημωt = k ( - x0 + x )
το μέγιστο μέτρο της δύναμης FΗ είναι το : k ( - x0 + x ) = k ( - x0 + Α2 ) = - mg + kΑ2
οριακή ισορροπία δοκού ροπές ως προς Δ : Στ(Δ) = 0 => mg l/4 = ( - mg + kΑ2 ) 5l/8 => 2mg/5 = - mg + kΑ2 => mg + 2mg/5 = kΑ2 => Α2 = 7mg / 5k = 7/5 x0
υ2 = ωΑ2 => υ2 = ω 7/5 mg / k = 7/5 g/ω άρα υ1 / υ2 = 5/7
η θετική κατεύθυνση είναι κατακόρυφη προς τα πάνω , το βάρος είναι προς τα κάτω άρα αρνητικό και η ροπή του βάρους κάθετη στο επίπεδο του σχήματος προς τα μέσα άρα αρνητική η δύναμη στο σημείο Η είναι προς τα πάνω διότι το σώμα Σ κινείται προς τα πάνω και συσπειρώνει το ελατήριο το οποίο ασκεί δύναμη στη δοκό προς τα πάνω άρα θετική και η ροπή της κάθετη στο επίπεδο του σχήματος προς τα έξω άρα θετική
ΘΕΜΑ Δ.
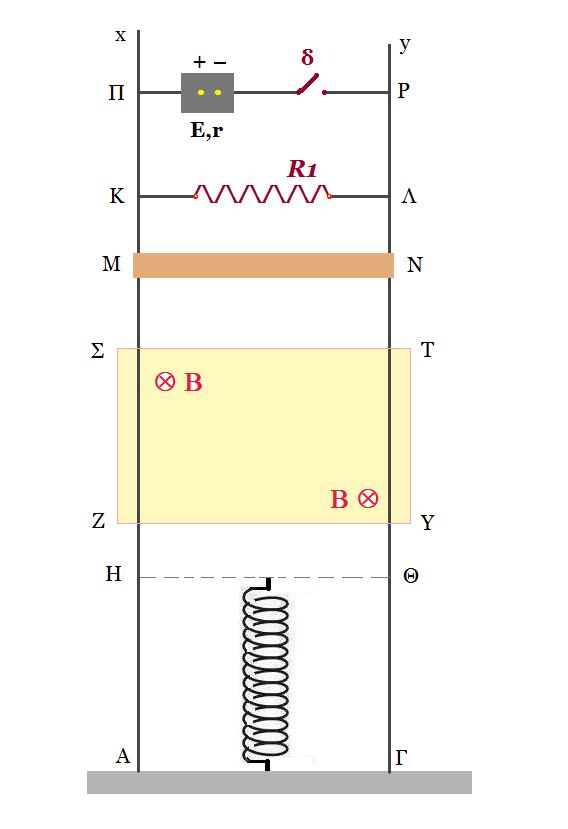
Δύο λεπτά κατακόρυφα σύρματα Αx και Γy, αμελητέας αντίστασης, είναι στερεωμένα σε μονωμένο οριζόντιο έδαφος. Τα δύο σύρματα έχουν μεγάλο μήκος και είναι παράλληλα μεταξύ τους, έχοντας απόσταση L = 1 m. Μεταξύ των σημείων Κ και Λ συνδέουμε αντιστάτη, ωμικής αντίστασης R1 = 0,8 Ω. Στο έδαφος στερεώνουμε κατακόρυφα ιδανικό ελατήριο, σταθεράς k = 100 N/m. Το φυσικό μήκος του ελατηρίου είναι στο οριζόντιο ευθύγραμμο τμήμα ΗΘ. Σε μία περιοχή υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο, έντασης μέτρου B = 1T με τις δυναμικές γραμές κάθετες στο επίπεδο των συρμάτων Αx και Γy. Η τομή του μαγνητικού πεδίου με το κατακόρυφο επίπεδο που ορίζουν οι δύο αγωγοί Αx και Γy είναι το ορθογώνιο παραλληλόγραμμο ΣΤΥΖ, όπου οι πλευρές ΣΤ και ΥΖ είναι οριζόντιες. Η ράβδος ΜΝ έχει μάζα m=0,5kg, μήκος L=1m, ωμική αντίσταση R2=0,2Ω και είναι συνεχώς σε επαφή με τα κατακόρυφα σύρματα Αx και Γy. Ανάμεσα στα σημεία Π και Ρ υπάρχει ηλεκτρική πηγή με ΗΕΔ E και εσωτερική αντίσταση r = 0,04 Ω, όπως επίσης και διακόπτης (δ).
Αρχικά ο διακόπτης (δ) είναι κλειστός και η ράβδος ισορροπεί μέσα στο ομογενές μαγνητικό πεδίο.
Δ1. Να υπολογίσετε την ΗΕΔ της ηλεκτρικής πηγής.
Ανοίγουμε τον διακόπτη (δ), ανεβάζουμε τη ράβδο ΜΝ σε ύψος h1 = 0,45 m πάνω από την πλευρά ΣΤ του ομογενούς μαγνητικού πεδίου και την αφήνουμε ελεύθερη. Η ράβδος εισέρχεται στο μαγνητικό πεδίο και έπειτα από λίγο εξέρχεται, έχοντας αποκτήσει οριακή ταχύτητα.
Δ2. Να υπολογίσετε την ένταση του ηλεκτρικού ρεύματος που θα διαρρέει το κύκλωμα, τη στιγμή που η ράβδος ΜΝ εισέρχεται στο μαγνητικό πεδίο.
Δ3. Να υπολογίσετε το μέτρο της οριακής ταχύτητας υορ που θα αποκτήσει η ράβδος ΜΝ μέσα στο ομογενές μαγνητικό πεδίο.
Δ4. Αν το ύψος του μαγνητικού πεδίου είναι (ΣΖ) = (ΤΥ) = h2 = 1 m, να υπολογίσετε το φορτίο q που μετακινήθηκε στο κύκλωμα, καθώς και το ποσό θερμότητας Q1 που εκλύθηκε από την αντίσταση R1, από τη στιγμή που η ράβδος εισήλθε μέχρι τη στιγμή που εξήλθε από το μαγνητικό πεδίο.
Δ5. Όταν η ράβδος ΜΝ εξέρχεται από το ομογενές μαγνητικό πεδίο, βρίσκεται σε ύψος h3 πάνω από το φυσικό μήκος του ελατηρίου. Η ράβδος καρφώνεται στο ελατήριο και αρχίζει να εκτελεί απλή αρμονική ταλάντωση, με σταθερά επαναφοράς D = k. Αν γνωρίζετε ότι το πλάτος της ταλάντωσης είναι Α = 9/20 m, να υπολογίσετε το ύψος h3.
Δ1. ισοοροπία ράβδου ΜΝ : m g = FL = B i2 l => 0,5 10 = 1 i2 1 => i2 = 5 A
VMN = i2 R2 = 5 A 0,2 Ω = 1 Volt
VΚΛ = i1 R1 => 1 V = i1 0,8 Ω => i1 = 1,25 A = 5/4 A i = i1 + i2 = 6,25 A
E = i { r + R1 R2 / ( R1 + R2 ) } = 6,25 { 0,04 + 0,2 0,8 / ( 0,2 + 0,8 ) } = 6,25 0,2 = 1,25 V
Δ2. h = ½ g t2 => 0,45 = ½ 10 t2 => t2 = 0,09 => t = 0,3 s v = g t = 10 0,3 = 3 m/s
η ράβδος ΜΝ μόλις εισέρχεται στο μαγνητικό πεδίο έχει ταχύτητα 3 m/s στα άκρα της θα αναπτυχθεί επαγωγική τάση Εεπαγ = Β υ l = 1 3 1 = 3 V με πολικότητα Μ(-) και Ν(+) τότε
Εεπαγ = i ( R1 + R2 ) => 3 = i 1 => i = 3 A
Δ3. Εεπαγ = Β υ l το κύκλωμα διαρρέεται με ρεύμα εντάσεως i = Εεπαγ / ( R1 + R2 )
η ράβδος MN δέχεται δύναμη Laplace FL = B i l = B2 l2 v / (R1 + R2) = 12 12 v / 1 = v
ΣF = m a => m g - FL = m a => 0,5 10 - v = 0,5 a => 5 - v = 0,5 a όταν α = 0 τότε υορ = 5 m/s οριακή ταχύτητα εξόδου
Δ4. q = ΔΦ / R = B A / R = 1 1 / 1 = 1 C
Καρχ + m g h2 = Κτελ + Qθερμ => ½ 0,5 32 + 0,5 10 1 = ½ 0,5 52 + Qθερμ =>
=> 9/4 + 5 = 25/4 + Qθερμ => 9/4 + 5 - 25/4 = Qθερμ => Qθερμ = - 1 J
|Qθερμ |= QR1 + QR2 = 1 J
QR1 / QR2 = ( i2 R1 t ) / ( i2 R2 t ) = R1 / R2 = 0,8 / 0,2 = 4
QR1 / QR2 = 4 => QR1 / (QR1 + QR2 ) = 4 / (4+1) => QR1 / 1 J = 4/5 => QR1 = 4/5 J = 0,8 J
Δ5. θέση ισορροπίας : m g = k x0 => 0,5 10 = 100 x0 => x0 = 0,05 m
Καρχ + m g h3 = Κτελ => ½ 0,5 52 + 0,5 10 h3 = ½ 0,5 v2 => 52 + 20 h3 = v2
για την ταλάντωση
½ k x02 + ½ m v2 = ½ k A2 => ½ 100 (1/20)2 + ½ 0,5 v2 = ½ 100 (9/20)2 =>
=> 100 1/400 + 0,5 v2 = 100 81/400 => 1/4 + 0,5 v2 = 81/4 =>
=> 0,5 v2 = 80/4 = 20 => v2 = 40
οπότε από την σχέση 52 + 20 h3 = v2 = 40 => 25 + 20 h3 = 40 => 20 h3 = 40 - 25 = 15 => h3 = 15/20 = 0,75 m