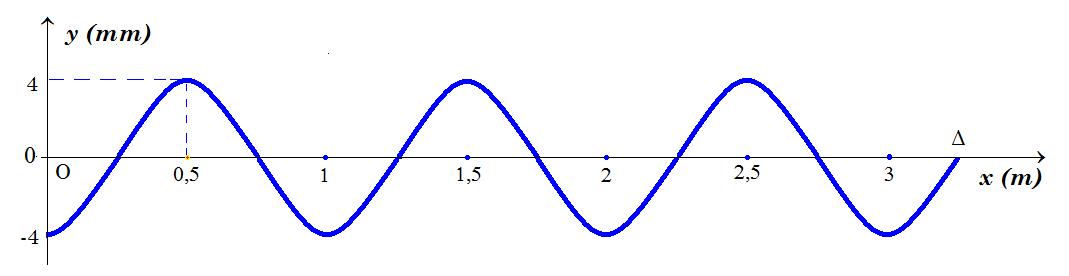
Κατά μήκος ενός γραμμικού ελαστικού μέσου, διαδίδεται ένα εγκάρσιο αρμονικό πλάτους Α=0,3m και στο σχήμα δίνεται το διάγραμμα της φάσης της απομάκρυνσης των  διαφόρων σημείων του μέσου, σε συνάρτηση με την θέση x (φ=f(x)) τη χρονική στιγμή t₁.

α)  Το κύμα διαδίδεται προς τα δεξιά (θετική φορά του άξονα) ή προς τα αριστερά;

β)  Να υπολογίσετε το μήκος του κύματος καθώς και την θέση x₁, όπου φτάνει το κύμα τη στιγμή t₁.

γ)  Να σχεδιάσετε την γραφική παράσταση της φάσης  (φ=f(x)) της απομάκρυνσης, την χρονική στιγμή t₂=t₁+2Τ, όπου Τ η περίοδος ταλάντωσης των σημείων του μέσου.

δ)  Αν η περίοδος ταλάντωσης των σημείων του μέσου είναι Τ=1s, ενώ t₁=2s:

    α)  Να βρεθεί η εξίσωση του κύματος.

    β)  Να σχεδιάσετε το στιγμιότυπο του κύματος τη χρονική στιγμή t₂=1s.

τη στιγμή t₁ : φ(x) = 3π + πx     φ = 0 => x = - 3 m      x  αυξάνεται  και  φ   αυξάνεται  το κύμα διαδίδεται προς τα αριστερά 

εξίσωση κύματος τη στιγμή t₁ :  y(x , t₁) = 0,3 ημ(3π + πx) = 0,3 ημ(2πt₁/T + πx + θ)      

        2π/λ = π => λ = 2 m           2πt₁/T + θ = 3π    

σε χρόνο Τ το κύμα διανύει απόσταση λ = 2 m   σε χρόνο 2Τ το κύμα διανύει απόσταση 2λ = 4 m  

  φ₁(x)  =  2πt₁/T + πx + θ  = 3π + πx

  φ₂(x)  =  2πt₂/T + πx + θ  =  2π(t₁+2Τ)/T + πx + θ  =  2πt₁/T + 4π + πx + θ  =  3π + πx + 4π =>  φ₂(x) = 7π + πx   

  T = 1 s     t₁ = 2 s        v = λ/T = 2m / 1s = 2 m/s η ταχύτητα διαδόσεως του κύματος

     φ₁  =  2πt₁/T + πx + θ  = 3π + πx  =>   2π2/1 + θ  = 3π  =>  θ = - π   

  άρα  η εξίσωση κύματος είναι :  y(x , t) =  0,3 ημ(2πt/T + πx - π)   

για t = 1s   έχουμε :  y(x , t=1s) =  0,3 ημ(2π1/1 + πx - π)  =  0,3 ημ(π + πx)  =  - 0,3 ημ(πx)     x ³ -1 m   διότι  π + πx ³ 0

ΘΕΜΑ Γ
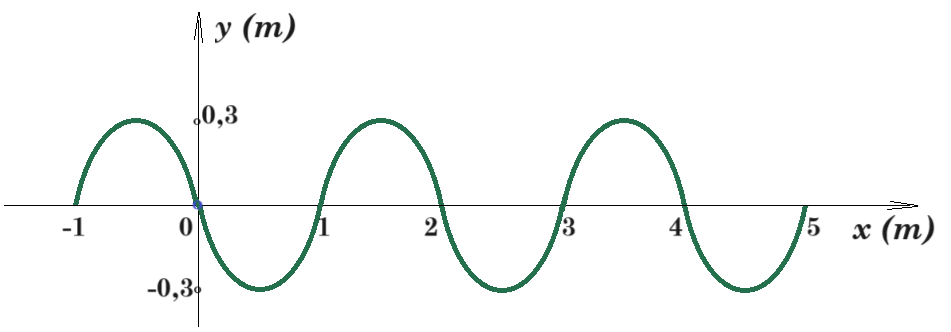
Η πηγή κύματος σημείο Ο (x=0) εκτελεί απλή αρμονική ταλάντωση, που περιγράφεται από την εξίσωση ψ=Aημωt. Το εγκάρσιο αρμονικό κύμα διαδίδεται κατά τη θετική φορά σε οριζόντια ελαστική χορδή που εκτείνεται κατά τη διεύθυνση του άξονα x'x. H απόσταση μεταξύ των δύο ακραίων θέσεων των σημείων είναι d=2 m. Η γραφική παράσταση της φάσης του κύματος φ σε σχέση με την απόσταση x από την αρχή του άξονα, τη στιγμή t₁=0,5 s που το κύμα φθάνει στο σημείο Κ,  έχει εξίσωση : φ(x) = 4π - 10πx, 0£x£0,4m. 
Γ1. Να γράψετε την εξίσωση του αρμονικού κύματος (S.I) που δημιουργείται.   (Μονάδες 5)
Γ2. Να υπολογίσετε την απομάκρυνση y, ενός σημείου όταν αυτό έχει ταχύτητα μέτρου υ=4π√3 m/s.  (Μονάδες 5)
Γ3. Τη στιγμή που η πηγή έχει ολοκληρώσει δύο ταλαντώσεις, να βρείτε την ταχύτητα ταλάντωσης v και την επιτάχυνση a,  ενός σημείου Λ της χορδής που βρίσκεται στη θέση x_Λ=0,2 m.  (Μονάδες 5)
Γ4. Να βρείτε τη διαφορά φάσης των σημείων Κ και Λ μετά την άφιξη του κύματος σε αυτά. (Μονάδες 5)
Γ5. Να απεικονίσετε το στιγμιότυπο του κύματος τη χρονική στιγμή Τ+Τ/4=0,3125 s και κατόπιν να βρείτε το πλήθος των σημείων που την ίδια χρονική στιγμή έχουν απομάκρυνση  y = - 0,5 m. (Μονάδες 5)  

Γ1.   y(x,t) = 1 ημ2π(t/T - x/λ)  

t = 0,5 s :   2π(0,5/T - x/λ)  =  π/T - 2πx/λ  =  4π - 10πx  =>   Τ = 1/4 s ,   λ = 0,2 m =1/5 m ,    υ = λ/Τ = 0,8 m/s  

  άρα    y(x,t) = 1 ημ2π(4t - x/0,2)  =>   y(x,t) = 1 ημ(8πt - 10πx)         υ(x,t) = 8π συν(8πt - 10πx)   

Γ2.   υ = 4π√3 m/s = 8π συν(8πt - 10πx)  =>  συν(8πt - 10πx) = 4π√3 / 8π = √3/2  

     άρα  ημ(8πt - 10πx) = ±½  =>  y = ±½ m

Γ3.  το κύμα φθάνει στο σημείο Λ μετά από   t = x/v = 0,2m / 0,8m/s = 0,25s ,  η πηγή ταλαντώνεται για χρόνο  t = 2T = 0,5 s , οπότε το σημείο Λ  στη θέση x = 0,2 m  ταλαντώνεται επί χρόνο  0,5s - 0,25s = 0,25s και  βρίσκεται σε απομάκρυνση από τη θέση ισορροπίας του :     y = 1 ημ(8πt - 10πx)  = 1 ημ(8π 0,25 - 10π 0,2)  = 1 ημ(2π - 2π) = 0

 v = 8π συν(8πt - 10πx)  = 8π συν(8π 0,25 - 10π 0,2)  = 8π συν(2π - 2π) = 8π m/s          a = 0  

Γ4.  το σημείο Κ απέχει από την πηγή :   x_K = v t = 0,8 m/s  0,5 s  = 0,4 m

            φ_Κ - φ_Λ  =   (8πt - 10π 0,4)   -  (8πt - 10π 0,2)  =  - 2π rad  

Γ5.   y(x, t=0,3125s) = 1 ημ(8π 0,3125 - 10πx)  =  1 ημ(2,5π  - 10πx)  = 1 συν(10πx)   0 £ x £ 0,25 m = λ + λ/4 

 y = - 0,5 m = 1 συν(10πx) =>   συν(10πx) = - 0,5 = συν(2π/3)  =>   10πx = 2Νπ + 2π/3  =>  x = Ν/5 + 1/15         0 £ x £ 0,25 m   => 0 £  Ν/5 + 1/15 £ 1/4  =>  - 5/15 £  Ν £  5/4 - 5/15 =>  - 1/3 £  Ν £  5/4 - 1/3  =>  Ν = 0 , 1    

Ν = 0   x = 1/15 m           N = 1    x = 1/5 + 1/15 = 2/15 m      

ΘΕΜΑ Δ
Κατά μήκος μιας χορδής μεγάλου μήκους, που ταυτίζεται με τον άξονα x'Ox, διαδίδονται ταυτόχρονα δύο αρμονικά κύματα που έχουν εξισώσεις  y₁=0,2ημ(20πt-10πx) (S.I.) και y₂=0,2ημ(20πt+10πx) (S.I.)   Τα δύο κύματα συμβάλλουν δημιουργώντας στο ελαστικό μέσο στάσιμο κύμα.
Δ1. Να γράψετε την εξίσωση του στάσιμου κύματος που δημιουργείται στη χορδή.    (Μονάδες 4)
Δ2. Να αποδείξετε ότι στην αρχή O(x=0) του άξονα δημιουργείται κοιλία και να διερευνήσετε αν στο σημείο B (x_B=0,25 m) σχηματίζεται δεσμός ή κοιλία.    (Μονάδες 4)
Δ3.  i) Να βρείτε το πλάτος της ταλάντωσης του υλικού σημείου Μ της χορδής που έχει τετμημένη x_M=0,025 m.

       ii) Ποιο το μέτρο της ταχύτητας ταλάντωσης υ_Μ του σημείου Μ όταν έχει  απομάκρυνση y_Μ=0,2 m;

      iii) Ποια είναι η απομάκρυνση y και ποιο είναι το μέτρο της ταχύτητας ταλάντωσης του σημείου Ο όταν η απομάκρυνση του σημείου Μ είναι y_M=0,2 m;     (Μονάδες 8)
Δ4. Να βρείτε το πλήθος των δεσμών στο ευθύγραμμο τμήμα ΜΡ και κατόπιν να βρείτε τη διαφορά φάσης μεταξύ του σημείου Μ και του σημείου Ρ (x_Ρ=0,30 m).    (Μονάδες 4)
Δ5. Να σχεδιάσετε το στιγμιότυπο του στάσιμου κύματος, από το σημείο Ο μέχρι το Ζ (x_Z=0,35 m) μια χρονική στιγμή που το σημείο Ο βρίσκεται στην μέγιστη θετική απομάκρυνση και κατόπιν να βρείτε το πλήθος των σημείων που εκείνη τη στιγμή έχουν απομάκρυνση y=+0,2 m.   (Μονάδες 5)

Δ.1.      y(x,t) = 0,4 συν(10πx) ημ(10πt)        10πx = 2πx/λ =>  λ = 0,2 m  

Δ.2.    y(x=0 , t) = 0,4 συν(10π 0) ημ(10πt)  = 0,4 1 ημ(10πt) => y(x=0 , t) = 0,4 ημ(10πt)

      y_B (x=0,25m , t) = 0,4 συν(10π 0,25) ημ(10πt)  = 0,4 0 ημ(10πt) = 0    δεσμός το σημείο Β

Δ.3.    y_Μ (x=0,025m , t) = 0,4 συν(10π 0,025) ημ(10πt)  = 0,4 √2/2 ημ(10πt) => y_Μ = 0,2.√2 ημ(10πt)     το σημείο Μ

      y_Μ = 0,2.√2 ημ(10πt) = 0,2  => ημ(10πt) = √2/2  => συν(10πt) = ±√2/2       υ_Μ  = 2.√2.π συν(10πt) = 2.√2.π ( ±√2/2 ) = ±2π m/s

   y(x=0 , t) = 0,4 ημ(10πt)  = 0,4  √2/2 = 0,2.√2 m           v(x=0 , t) = 4π συν(10πt)  =  4π ( ±√2/2 ) =  ±2√2π m/s  

Δ.4.   y_Ρ (x=0,3m , t) = 0,4 συν(10π 0,3) ημ(10πt)  = 0,4 συν(3π) ημ(10πt) => y_Μ = -0,4 ημ(10πt)     το σημείο Ρ              τα σημεία Μ και Ρ έχουν διαφορά φάσης  π  

     0        0,025      0,05                0,1                                  0,2                  0,25                 0,3              0,35

    O           M                                                                                               B                    P                 Ζ

     κ                        δ                    κ                  δ                  κ                     δ                    κ                 δ

Δ.5.  

ΘΕΜΑ 4
Ένα σώμα Σ μάζας 𝑚 = 2𝑘𝑔 κρέμεται από το κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k.  Το πάνω άκρο του ελατηρίου είναι στερεωμένο ακλόνητα σε οροφή.  Τη χρονική στιγμή 𝑡₀ = 0 εκτοξεύουμε το σώμα από τη θέση ισορροπίας του με ταχύτητα 𝜐⃗₀ κατακόρυφα προς τα πάνω.  Το σώμα εκτελεί απλή αρμονική ταλάντωση με πλάτος 𝛢 = 0,2 𝑚.  Την προς τα πάνω κατεύθυνση λαμβάνουμε ως θετική.  Τη χρονική στιγμή 𝑡₁ = 𝜋/10𝑠  το σώμα περνά για πρώτη φορά μετά την εκτόξευση από τη θέση ισορροπίας του.
Δίνεται η επιτάχυνση βαρύτητας 𝑔 = 10 𝑚/𝑠².
4.1.  Να υπολογίσετε την περίοδο της ταλάντωσης και να γράψετε την εξίσωση της απομάκρυνσης της ταλάντωσης του σώματος.       Μονάδες 8
4.2.  Να υπολογίσετε τη σταθερά επαναφοράς 𝐷 και το μέτρο της αρχικής ταχύτητας 𝜐⃗₀.       Μονάδες 7
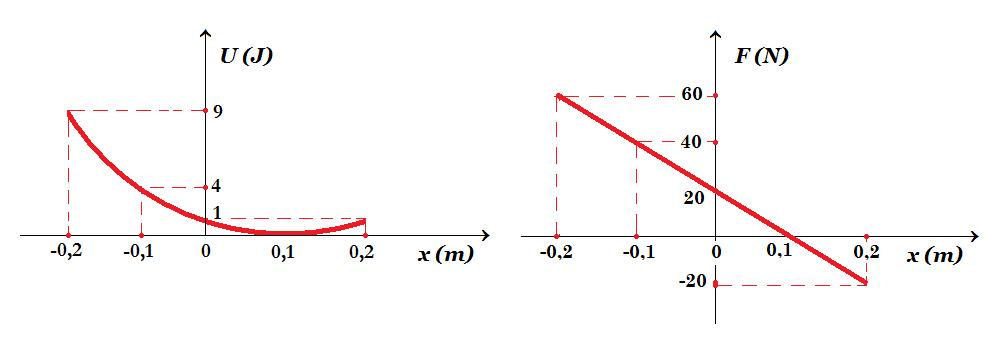
4.3.  Να γράψετε τη συνάρτηση που περιγράφει τη δύναμη που ασκεί το ελατήριο στο σώμα Σ σε σχέση με την απομάκρυνση και τη συνάρτηση που περιγράφει τη δυναμική ενέργεια του ελατηρίου σε σχέση με την απομάκρυνση. Να παραστήσετε γραφικά κάθε σχέση σε αριθμημένους άξονες.          Μονάδες 10

Θέμα #24452

4.1.      Τ = 2 π/10 s = π/5 s    ω = 2π/Τ = 10 rad/s        x = A ημωt  =>  x(t)  =  0,2 ημ10t   

4.2.   D  = k = m ω²  = 2 100 = 200 N/m       v₀ = ω Α = 10 rad/s  0,2 m = 2 m/s  αρχική ταχύτητα

4.3.   x(t) = 0,2 ημ10t      v(t) = 2 συν10t       α(t) = - 20 ημ10t   

  θέση ισορροπίας :  m g = k x₀  =>  x₀ = 20/200 = 0,1 m   επιμήκυνση  

   επειδή η θετική κατεύθυνση είναι προς τα πάνω  τότε  x₀ = - 0,1 m

 ΣF = m a  =>  F_ελατ - mg  = m a  => F_ελατ  - 20  =  2 [ - 20 ημ10t ]  =>  F_ελατ(t) = 20  - 40 ημ10t      F_ελατ(0)  =  20 N   

 ΣF = - D x  => F_ελατ - mg = - D x  =>  F_ελατ(x) = 20 - 200x =  - 200 (x - 0,1)   [-0,2m , 0,2m]       F_ελατ(0)  =  20 N   

 U_{ταλάντωσης}  =  ½ D x²  =  ½  200 x²  = 100 x²       [-0,2m , 0,2m]                          

 U_{ελατηρίου}  =  ½ D (x + x₀)²  =  ½  200 (x - 0,1)²  = 100 (x - 0,1)²     [-0,2m , 0,2m]             

 x = - 0,2 m     U_{ελατηρίου}  = 100 ( -0,2 - 0,1)²  =  100  (-0,3)²  =  9 J    

                        F_ελατ(-0,2) = - 200 (-0,2 - 0,1) = - 200  (- 0,3)  =  60 Ν     το ελατήριο έχει μέγιστη επιμήκυνση

 x = - 0,1 m     U_{ελατηρίου}  = 100 ( - 0,1 - 0,1 )²  =  100  (-0,2)²  =  4 J           

                        F_ελατ(-0,1) = - 200 ( - 0,1 - 0,1) = - 200  (-0,2)  =  40 Ν  

 x = 0 m     U_{ελατηρίου} = 100  (-0,1)²  = 1 J        F_ελατ(0) = - 200 (-0,1) = 20 Ν  το σώμα διέρχεται από τη θέση ισορροπίας του

 x = + 0,1 m     U_{ελατηρίου}  = 100 (0,1 - 0,1)²  =  0 J    

                        F_ελατ(+0,1) = - 200 (0,1 - 0,1) =  0 Ν   το ελατήριο έχει το φυσικό του μήκος

 x = + 0,2 m     U_{ελατηρίου}  = 100 (0,2 - 0,1)²   =  100  0,1²  =  1 J

                        F_ελατ(+0,2) = - 200 (0,2 - 0,1) = - 200 0,1 = - 20 Ν     το ελατήριο έχει μέγιστη συσπείρωση

ΘΕΜΑ 4
Για τη μελέτη των στάσιμων κυμάτων κατά μήκος τεντωμένης χορδής δημιουργήθηκε στο εργαστήριο πειραματική διάταξη που αποτελείται από έναν ταλαντωτή, μία τροχαλία, μία αβαρή ελαστική χορδή και διάφορα σταθμά. Ο ταλαντωτής συνδέεται με μία γεννήτρια συχνοτήτων.  Όταν η χορδή ηρεμεί έχει μήκος L = 1,6 m.  Η γεννήτρια τίθεται σε λειτουργία και ρυθμίζουμε την συχνότητά της ώστε να σχηματιστεί το στάσιμο κύμα του παρακάτω σχήματος.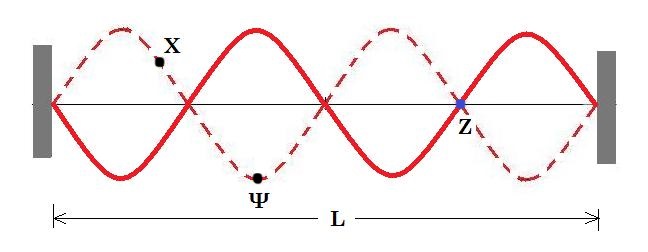 Τα σημεία που συνδέεται η χορδή με τον ταλαντωτή και την τροχαλία, μετά τον σχηματισμό του στάσιμου κύματος θεωρούνται ακίνητα, δηλαδή συμπεριφέρονται όπως το σημείο Ζ.  Η μέγιστη απομάκρυνση από την θέση ισορροπίας των σημείων που βρίσκονται στις κοιλίες π.χ. το Ψ, είναι 4 cm.  Το ελάχιστο χρονικό διάστημα που χρειάζεται το σημείο Χ για να κινηθεί από την μία ακραία θέση ταλάντωσης στην άλλη είναι Δt = 0,1s.
4.1.  Να βρεθεί το μήκος κύματος των αρμονικών κυμάτων που δημιουργούν το στάσιμο κύμα στην χορδή καθώς και η ταχύτητα διάδοσης του αρμονικού κύματος στην χορδή.       Μονάδες 6
4.2.  Να υπολογίσετε πόσο πρέπει να μεταβληθεί η συχνότητα της γεννήτριας ώστε να σχηματιστεί στην χορδή ένα ακόμη σημείο δεσμού.           Μονάδες 6
4.3.  Για την αρχική συχνότητα του ταλαντωτή να γραφεί η εξίσωση του στάσιμου κύματος του παραπάνω σχήματος, καθώς και η εξίσωση που δίνει την επιτάχυνση ταλάντωσης των μορίων της χορδής σε συνάρτηση με τον χρόνο.  Θεωρούμε ως t = 0 τη στιγμή που όλα τα μόρια της χορδής διέρχονται από την θέση ισορροπίας τους και η ταχύτητα του σημείου στην θέση Ψ είναι υ > 0.  Ορίζουμε την θέση του σημείου Ψ ως την αρχή του οριζόντιου άξονα με x = 0.  Να θεωρήσετε ότι π² = 10.       Μονάδες 6
4.4.  Για την αρχική συχνότητα του ταλαντωτή να βρεθεί το μέτρο της ταχύτητας ταλάντωσης των μορίων της χορδής του παραπάνω σχήματος τα οποία βρίσκονται στις θέσεις των κοιλιών, όταν βρεθούν σε απομάκρυνση y = √7 cm από την θέση ισορροπίας.       Μονάδες 7

Θέμα   Δ  23245   

4.1.   2 λ = L  = 1,6 m   =>  λ = 0,8 m        2 A = 4 cm  =>  A = 2 cm = 0,02 m          T / 2 = 0,1 s  =>  T = 0,2 s  

                 f = 1/T = 5 Hz               v = λ / T = 0,8m / 0,2s = 4 m/s   

4.2.   2,5 λ' = L  = 1,6 m   =>  λ' = 0,64 m     f ' = v / λ' = 4 m/s / 0,64 m  = 6,25 Hz     

4.3.   y(x , t)  =  0,04  συν(2πx/λ)  ημ(2πt/Τ)  =  0,04 συν(2πx/0,8)  ημ(2πt/0,2) =>  y(x , t) = 0,04 συν(2,5πx)  ημ(10πt)  

       υ(x , t) = 0,4π  συν(2,5πx)  συν(10πt)            α(x , t) = - 40  συν(2,5πx)  ημ(10πt)  

      υ(x=0 , t=0) = 4π  συν( 0 )  συν( 0 )  =  4π m/s > 0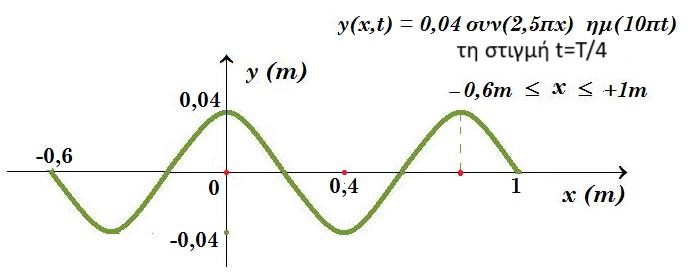  

4.4.    έστω το σημείο  με  x=0,4m  που είναι κοιλία

  τότε   y(x=0,4m , t)  =  0,04 συν(2,5π 0,4)  ημ(10πt)  = √7 10^-2 m   =>  συν(π)  ημ(10πt)  =  √7/4  =>  ημ(10πt) = -√7/4  

  οπότε   συν²(10πt)  =  1  -  7/16  =  (16 - 7) / 16 =  9/16    =>   συν(10πt) = ± 3/4  

   άρα     υ(x=0,4m , t) =  0,4π  συν(π)  συν(10πt)  =  0,4π  (-1) (± 3/4)  =  ± 0,3π m/s  

 έστω το σημείο  με  x=0,8m  που είναι κοιλία

  τότε   y(x=0,8m , t)  =  0,04 συν(2,5π 0,8)  ημ(10πt)  = √7 10^-2 m   =>  συν(2π)  ημ(10πt)  =  √7/4  =>  ημ(10πt) = +√7/4  

  οπότε   συν²(10πt)  =  1  -  7/16  =  (16 - 7) / 16 =  9/16    =>   συν(10πt) = ± 3/4  

   άρα     υ(x=0,8m , t) =  0,4π  συν(2π)  συν(10πt)   =  0,4π  (-1) (± 3/4)  =  ± 0,3π m/s  

ΘΕΜΑ 4
Η εξίσωση της ταχύτητας ενός απλού αρμονικού ταλαντωτή δίνεται από την σχέση υ = 4π.συν(10πt)  S.I.
4.1. Να υπολογίσετε το πλάτος ταλάντωσης και την περίοδο ταλάντωσης του ταλαντωτή.  Μονάδες 6
4.2. Να γράψετε την εξίσωση επιτάχυνσης για τον απλό αρμονικό ταλαντωτή.         Μονάδες 6
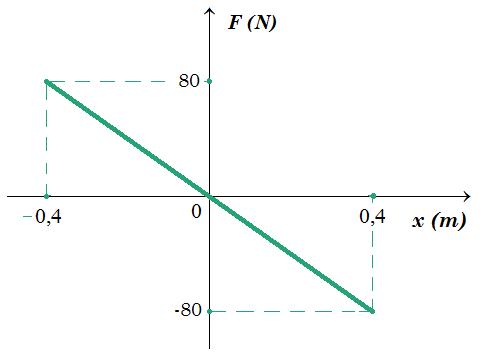
4.3. Αν ο ταλαντωτής έχει μάζα m = 200g, να σχεδιάσετε τη γραφική παράσταση της δύναμης
επαναφοράς σε συνάρτηση με την απομάκρυνση από την θέση ισορροπίας.       Μονάδες 7
4.4. Μετά από αρκετό χρόνο επεμβαίνει στο σύστημα ένα εξωτερικό αίτιο, το οποίο ασκεί δύναμη της
μορφής F = F₀ συν(20πt) στο S.I.  Να βρείτε την περίοδο ταλάντωσης του συστήματος και να εξετάσετε αν το σύστημα θα βρεθεί σε συντονισμό. Δίνεται π² ≈ 10.           Μονάδες 6

Θέμα Δ    23136

  v  =  4π συν(10πt)        x  =  0,4 ημ(10πt)         a  = - 40π² ημ(10πt)        Τ = 2π/ω = 2π / 10π = 0,2s    f = 1/T = 5 Hz  

  ΣF  =  m a  =  0,2  [ - 40π² ημ(10πt) ]  = - 80 ημ(10πt)  = - 200 x      - 0,4 m £ x £ + 0,4 m   

  D = m ω² = 0,2  100π²  =  200 N/m  

  F = F₀ συν(20πt)    ω_δ = 20π rad/s  = 2π/Τ_δ  =>  Τ_δ = 0,1 s      f_δ = 1/ Τ_δ = 10 Hz       f <  f_δ    δεν έχουμε συντονισμό

ΘΕΜΑ 4
Πηγή κύματος Ο αρχίζει τη χρονική στιγμή 𝑡=0 να εκτελεί απλή αρμονική ταλάντωση, που περιγράφεται από την εξίσωση 𝜓 = 𝐴.𝜂𝜇𝜔𝑡. Το εγκάρσιο αρμονικό κύμα πλάτους 𝛢 = 0,05 𝑚 διαδίδεται κατά τη θετική φορά σε οριζόντια ελαστική χορδή που εκτείνεται κατά τη διεύθυνση του άξονα 𝑥′𝑥. Θεωρούμε ότι το σημείο της χορδής στη θέση 𝑥 = 0 τη χρονική στιγμή 𝑡 = 0 έχει μηδενική απομάκρυνση από τη θέση ισορροπίας του και θετική ταχύτητα.
Η γραφική παράσταση της φάσης του κύματος 𝜑, την χρονική στιγμή 𝑡₁ = 0,5 𝑠 , σε σχέση με την απόσταση 𝑥 από την αρχή του άξονα (𝑥 = 0) παριστάνεται στο διάγραμμα.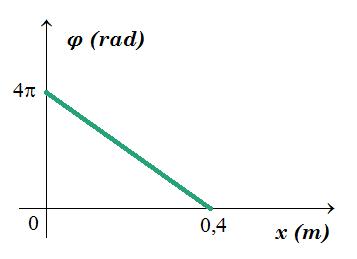 

4.1.  Να γράψετε την εξίσωση του αρμονικού κύματος (𝑆.𝐼) που δημιουργείται.      Μονάδες 6
4.2.  Να υπολογίσετε την απομάκρυνση από τη θέση ισορροπίας του ενός σημείου του ελαστικού μέσου, που βρίσκεται στη θέση 𝑥 = 0,4 𝑚 τη χρονική στιγμή 0,5625𝑠.       Μονάδες 6
4.3.  Να υπολογίσετε την ταχύτητα ταλάντωσης και την επιτάχυνση ενός υλικού σημείου της χορδής που βρίσκεται στη θέση 𝑥 = 0,2 𝑚 τη χρονική στιγμή 0,5 𝑠 .     Μονάδες 6
4.4.  Να απεικονίσετε το στιγμιότυπο του κύματος τη χρονική στιγμή  𝛵 + 𝛵/4 = 0,3125 𝑠    Μονάδες 7

Θέμα Δ   27964

4.1.  από το διάγραμμα έχουμε  φ ( x , t=0,5s ) = 4π - 10πx  =  2π 0,5/T -  2πx/λ  =>     f = 4 Hz      T = 1/4 s       λ = 1/5 m     v = λ f = 0,8 m/s

  y(x,t) = Α ημ(2πt/Τ - 2πx/λ) = 0,05 ημ(8πt - 10πx)        y(x,t=0,5s) =  0,05 ημ(8π 0,5 - 10πx) =  0,05 ημ(4π - 10πx)   

4.2.   y(x=0,4m , t=0,5625s)  =  0,05  ημ(8π 0,5625  -  10π 0,4)  =  0,05  ημ(4,5π  -  4π) =  0,05  ημ(π/2)  = 0,05 m    

4.3.   y(x,t) = 0,05 ημ(8πt - 10πx)          v(x,t) = 0,4π συν(8πt - 10πx)  =>  v(x=0,2m , t=0,5s) = 0,4π συν(8π 0,5 - 10π 0,2) =  0,4π  συν(4π  -  2π)  =  + 0,4π m/s    

  a(x,t)  =  - 3,2π²  ημ(8πt  -  10πx)   =>  a(x=0,2m , t=0,5s)  = - 3,2π²  ημ(8π 0,5  -  10π 0,2) = - 3,2π²  ημ(4π - 2π)  =  0  

4.4.   y(x , t=0,3125s)  =  0,05  ημ(8π 0,3125 - 10πx)  =  0,05 ημ(5π/2 - 10πx)  = 0,05 συν(10πx)    0 £ x £ 0,25 m    

       x = v t =  0,8 m/s  0,3125 s =  0,25 m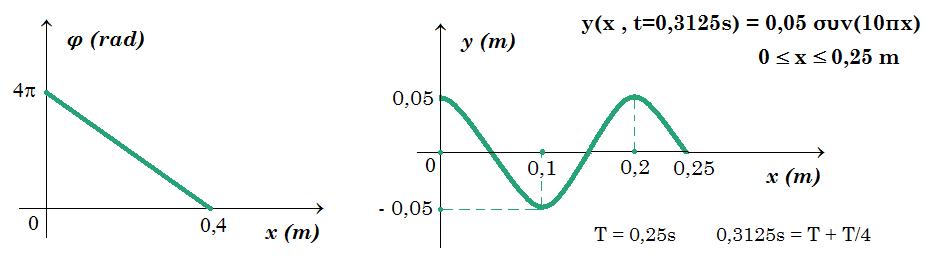  

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Ένα σώμα Σ μάζας  m = 0,5 kg   εκτελεί Α.Α.Τ.  με πλάτος  Α = 0,2 m.  Η φάση της απλής αρμονικής ταλάντωσης μεταβάλλεται με το χρόνο όπως φαίνεται στο διάγραμμα: 

Γράψτε την εξίσωση της επιτάχυνσης του σώματος συναρτήσει του χρόνου.  

Γράψτε την εξίσωση της συνισταμένης δύναμης  που ασκείται στο σώμα συναρτήσει του χρόνου.       

Γράψτε την εξίσωση της δυναμικής ενέργειας    και   της κινητικής ενέργειας  του σώματος συναρτήσει του χρόνου.  

Γράψτε την εξίσωση του ρυθμού μεταβολής της δυναμικής ενέργειας    και   της κινητικής ενέργειας  του σώματος συναρτήσει του χρόνου.  

Από την ταλάντωση του σώματος Σ  δημιουργείται  εγκάρσιο κύμα το οποίο διαδίδεται στον γύρω από το σώμα χώρο, τον οποίο θεωρούμε ελαστικό μέσο,  με ταχύτητα υ = 0,3 m/s.   Το σώμα Σ γίνεται πηγή κυμάτων,   σε απόσταση x  από την πηγή   θεωρούμε  στοιχειώδη μάζα   Δm = 1 μg.    

Γράψτε την εξίσωση της απομάκρυνσης της στοιχειώδους μάζας Δm   συναρτήσει του χρόνου.    

Γράψτε την εξίσωση της συνισταμένης δύναμης  που ασκείται στη στοιχειώδη μάζα Δm συναρτήσει του χρόνου.     

Ποιά είναι η διαφορά φάσης μεταξύ της στοιχειώδους μάζας Δm  και  της πηγής των κυμάτων;

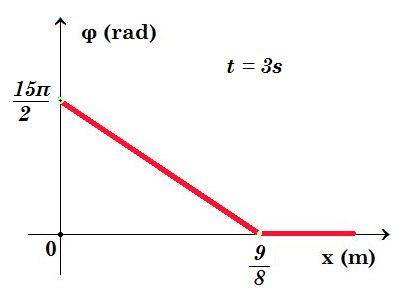
Σχεδιάστε το στιγμιότυπο του κύματος την χρονική στιγμή  t = 3 s.

Να βρεθεί η φάση της απομάκρυνσης της ταλάντωσης σημείου Κ, στη θέση  x_K = 1,5 m, σε συνάρτηση με το χρόνο και να γίνει η γραφική της παράσταση για t ≤ 2,5s.

  ω = Δφ/Δt = ( 11π/2 - 3π/2 ) / 2 = 2π rad/s      Τ = 2π/ω = 2π / 2π = 1s      

 y(t) = A ημ(ωt + φ₀) =>   y(t) = 0,2 ημ(2πt + 3π/2)         υ(t) = 0,4π συν(2πt + 3π/2)           α(t) = - 0,8π² ημ(2πt + 3π/2)  

  ΣF = m a  = 0,5  { - 0,8π² ημ(2πt + 3π/2) }  = - 0,4π² ημ(2πt + 3π/2)        

   U =  ½ D y²  =  ½ m ω² y²  =   ½  0,5  (2π)²  0,2² ημ²(2πt + 3π/2)  = 0,04π² ημ²(2πt + 3π/2)            

    Κ =  ½ m υ²  =   ½  0,5  (0,4π)² συν²(2πt + 3π/2)  =  0,04π² συν²(2πt + 3π/2) 

dU/dt = m ω² y(t)  v(t)  =  0,5 (2π)² 0,2 ημ(2πt + 3π/2)  0,4π συν(2πt + 3π/2) = 0,16π³ ημ(2πt + 3π/2)  συν(2πt + 3π/2)  

dΚ/dt =  m  υ(t)  a(t) =  0,5  0,4π συν(2πt + 3π/2)  { - 0,8π² ημ(2πt + 3π/2) }  =  - 0,16π³ συν(2πt + 3π/2)  ημ(2πt + 3π/2)

   v = λ/T  =>   λ = v T = 0,3 m/s  1 s  =>  λ =  0,3 m        

         y(t,x) = A ημ(2πt/Τ - 2πx/λ + φ₀)  =>   y(t,x) =  0,2 ημ(2πt/1 - 2πx/0,3 + 3π/2)   =>

                                                                 =>  y(t,x) =  0,2 ημ(2πt - 20πx/3 + 3π/2)    

    v(t,x) =  0,4π συν(2πt  - 20πx/3 + 3π/2)                   α(t,x) =  - 0,8π² ημ(2πt  - 20πx/3 + 3π/2)

    ΣF =  Δm a  =  10^-9  { - 0,8π² ημ(2πt  - 20πx/3 + 3π/2) }  = - 0,8π² 10^-9 ημ(2πt  - 20πx/3 + 3π/2)    

     Δφ  =  φ_Δm  -  φ_πηγής  =  (2πt  - 20πx/3 + 3π/2)  - (2πt + 3π/2)  =  - 20πx/3        

 y(t=3s , x) = 0,2 ημ(2π 3 - 20πx/3 + 3π/2) = 0,2 ημ(15π/2 - 20πx/3)  = - 0,2 συν(20πx/3)  

      x = v t = 0,3 m/s 3 s = 0,9 m            t = 3 s = 3 T  

  φ(x) = 15π/2 - 20πx/3           φ = 0  =>  x = 45 / 40 m = 9/8 m               φ(0) = 15π/2      

  1,5 = 0,3 ^. 5 = 5λ     φ_K = (2πt - 20π 1,5/3 + 3π/2) = (2πt - 10π + 3π/2) = (2πt - 17π/2)      φ_Κ = 0  =>  t = 17/4 s  

    φ_Κ = π(t - (-1)/2)  = π(t + 1/2)  = πt + π/2          φ_Κ = 0  => πt + π/2 = 0  =>   t = - 0,5 s            t = 0  => φ_Κ = π/2               t = 2,5 s  =>  φ_Κ = 5π/2 + π/2  = 3π rad     

.............................................................................................................................................

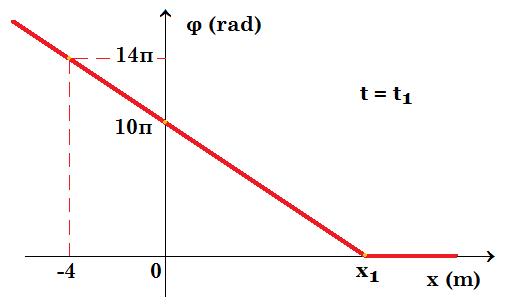
Κατά μήκος ενός γραμμικού ελαστικού μέσου, διαδίδεται ένα εγκάρσιο αρμονικό πλάτους Α=0,2m και στο σχήμα δίνεται το διάγραμμα της φάσης της απομάκρυνσης των  διαφόρων σημείων του μέσου, σε συνάρτηση με την θέση x (φ=f(x)) τη χρονική στιγμή t₁.

1. Το κύμα διαδίδεται προς τα δεξιά (θετική φορά του άξονα) ή προς τα αριστερά;
2.  Να υπολογίσετε το μήκος του κύματος καθώς και την θέση x₁, όπου μηδενίζεται η φάση τη στιγμή t₁.
3. Να σχεδιάσετε την γραφική παράσταση της φάσης  (φ=f(x)) την χρονική στιγμή t₂=t₁+Τ, όπου Τ η περίοδος ταλάντωσης των σημείων του μέσου.
4. Αν το κύμα ικανοποιεί την εξίσωση  y(t,x) = Α∙ημ2π(t/Τ - x/λ)  να σχεδιάστε ένα στιγμιότυπο του κύματος την στιγμή t₁, αν Τ=1s.
5. Να σχεδιάσετε την γραφική παράσταση της απομάκρυνσης y=f(t) για ένα σημείο Σ, στην θέση x=-4m, μέχρι τη στιγμή t₁.

 1.     φ(x)  =  10π + a x  =>  14π = 10π + a (-4)  =>  a = - π           φ(x)  =  10π - πx  =  2π ( 5 - x/2 )         Το κύμα διαδίδεται προς τα δεξιά (θετική φορά του άξονα)

2.   λ = 2 m           φ(x₁)  = 0  =>  2π ( 5 - x₁ /2 )  =  0  =>  x₁ = 10 m   =  5 ^. 2 m  =  5λ        

3.   t₁ /T = 5   =>  t₁ = 5T             t₂ = 6T      x₂ = 12 m            φ(x)  =  2π ( 6 - x/2 )

4.  Τ = 1s      φ(x) = 2π ( 5 - x/2 )        y = 0,2 ημ 2π ( 5 - x/2 )  =  0,2 ημ(- πx) =  - 0,2 ημ(πx)      t₁ = 5T    5 περίοδοι  

5.   t = x/v = 4m / 2m/s = 2s   το κύμα φθάνει στο σημείο Σ σε χρόνο 2s  πριν τη στιγμή t=0

    y = 0,2 ημ 2π ( t - (-4)/2 )  =  0,2 ημ 2π (t + 2)          y = 0 => t = -2s           y =  0,2 ημ(2πt)     - 2s £  t £  5s   

................................................................................................................................

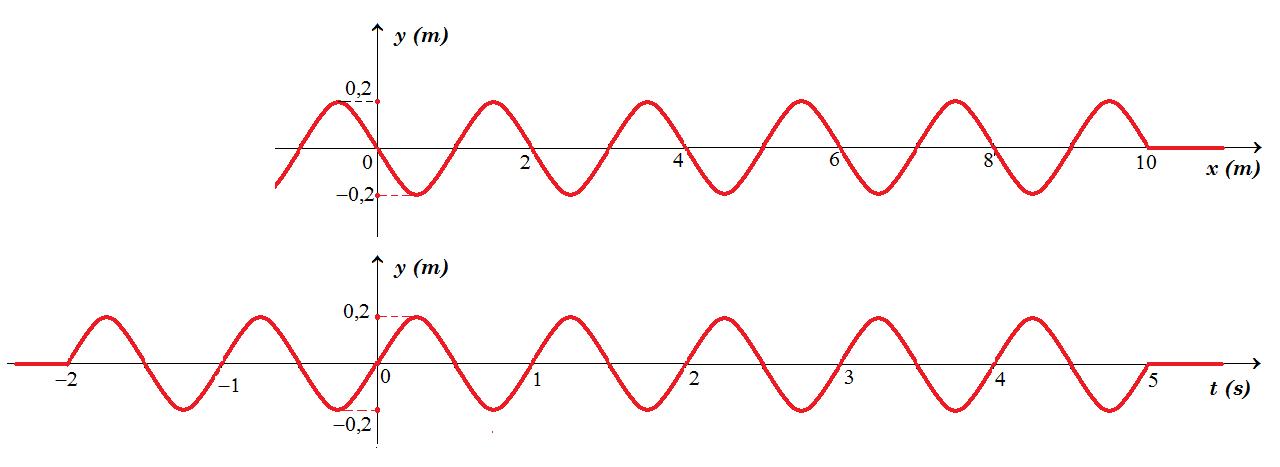
Ένα εγκάρσιο αρμονικό κύμα διαδίδεται κατά μήκος ενός γραμμικού ελαστικού μέσου, προς τα δεξιά (θετική κατεύθυνση) και τη στιγμή t=0 φτάνει στο σημείο Ο, στη θέση x=0. Το σημείο Ο ξεκινά την ταλάντωσή κινούμενο προς τα πάνω (θετική φορά) και φτάνει στην ακραία θέση του, σε απόσταση 0,2m σε χρονικό διάστημα Δt=0,5s, ενώ στο μεταξύ το κύμα έχει διαδοθεί φτάνοντας στο σημείο Λ, όπου (ΟΛ)=1m.

1. Να υπολογισθεί η ταχύτητα διάδοσης του κύματος, καθώς και η εξίσωση του κύματος.
2. Να βρεθεί η φάση της απομάκρυνσης της ταλάντωσης του σημείου Κ, στη θέση x₁=-1m, σε συνάρτηση με το χρόνο και να γίνει η γραφική της παράσταση για t ≤ 2,5s.
3. Να βρεθούν οι θέσεις των σημείων, τα οποία τη στιγμή t₁=2,5s έχουν μέγιστη κατά μέτρο ταχύτητα ταλάντωσης, στην περιοχή -2m ≤ x ≤ 2 m.
4. Να σχεδιάστε το στιγμιότυπο του κύματος τη χρονική στιγμή t₂=3s.
5. Να βρεθεί η θέση του σημείου Σ του μέσου, το οποίο την στιγμή t₃=6,5s έχει πραγματοποιήσει 43,5 ταλαντώσεις.

Θεωρούμε ότι η πηγή είναι σε μεγάλη απόσταση από την αρχή Ο (x=0) του άξονα.

1.       A = 0,2 m     T/4 = 0,5 s  =>  T = 2 s                 λ/4 = 1 m => λ = 4 m            υ  = λ/Τ = 4 / 2 = 2 m/s                  y(x,t) = 0,2 ημ2π(t/2 - x/4)  =  0,2 ημπ(t - x/2)       υ(x,t) =  0,2π συνπ(t - x/2)
2.     φ_Κ = π(t - (-1)/2)  = π(t + 1/2)  = πt + π/2          φ_Κ = 0  => πt + π/2 = 0  =>   t = - 1/2 s            t = 0  => φ_Κ = π/2               t = 2,5 s  =>  φ_Κ = 5π/2 + π/2  = 3π rad     
3.   t = 2,5 s     φ = π(t - x/2)  = π(5/2 - x/2)         υ = 0,2π  => συνπ(5/2 - x/2) = ±1  =>   π(5/2 - x/2) =  Νπ  =>  πx/2 =  - Νπ  +  5π/2   =>  x =  - 2Ν  +  5         -2m ≤ x ≤ 2 m  =>   -2m ≤  - 2Ν  +  5  ≤ 2 m   =>  -2  -  5   ≤  - 2Ν   ≤ 2   -  5    =>  -7    ≤  - 2Ν   ≤   -3    =>  3/2    ≤  Ν   ≤   7/2     =>   Ν = 2,  3         Ν = 2  => x =  - 2 2  +  5  =  + 1 m       Ν = 3  => x =  - 2 3  +  5  =  - 1 m       
4.     t = 3 s        y(x,3) =  0,2 ημπ(3 - x/2) =  0,2 ημ (3π - πx/2) =  0,2 ημ (πx/2)            φ = 0  => x = 6 m       φ(0) = 3π rad   => x = 0    
5.    t = 6,5 s     T = 2s  =>  f = 0,5 Hz      f = N / t  =>    43,5 ταλαντώσεις  / 0,5 Hz  =  t  =>  t = 87 s           43,5 ταλαντώσεις  σημαίνει ότι η φάση είναι  φ = 43,5  2π rad    για χρόνο  t = 6,5 s   οπότε έχουμε :    φ  = π(t - x/2)  =>  43,5  2π  =  π(6,5 - x/2)  =>   87  =  13/2 - x/2  =>   x  =  - 87 2 + 13 =  - 174  +  13 =  - 161 m    το σημείο είναι αριστερά από την θέση Ο  σε απόσταση 161 m

................................................................................................................................

ΘΕΜΑ 4 
Υλικό σημείο O ομογενούς ελαστικής χορδής, που έχει επιλεγεί ως αρχή των αξόνων (𝑥 = 0), αρχίζει τη
χρονική στιγμή 𝑡 = 0 να ταλαντώνεται σύμφωνα με την εξίσωση 𝑦 = 𝐴𝜂𝜇(𝜔𝑡) και κάθετα στη διεύθυνση
της χορδής. Η κινητική ενέργεια της ταλάντωσης του υλικού σημείου Ο μηδενίζεται 20 φορές σε κάθε
χρονικό διάστημα 𝛥𝑡 = 5 𝑠. Το κύμα που παράγεται διαδίδεται κατά την αρνητική φορά του άξονα 𝑥'𝛰𝑥
κατά μήκος της χορδής που διέρχεται από το σημείο Ο με ταχύτητα 𝜐 = 2 𝑚/𝑠. Στη διάρκεια μιας
περιόδου της ταλάντωσής του το υλικό σημείο O διανύει διάστημα 𝑠 = 0,2 𝑚.
4.1.   Να γράψετε την εξίσωση του κύματος που παράγεται.               Μονάδες 7
4.2.   Να υπολογίσετε τη χρονική στιγμή που αρχίζει να κινείται ένα σημείο Μ, που βρίσκεται στη θέση
𝑥_𝑀 = −1 𝑚 της χορδής όπως επίσης και την απομάκρυνση 𝑦_𝑀, από τη θέση ισορροπίας του σημείου
Μ, τη χρονική στιγμή 𝑡 = 13/24 𝑠.             Μονάδες 6
4.3.   Να σχεδιάσετε το διάγραμμα της φάσης του κύματος σε συνάρτηση με τη συντεταγμένη της θέσης  (𝜑 − 𝑥),  τη χρονική στιγμή 𝑡 = 2 𝑠.             Μονάδες 6
4.4.    Να βρείτε τις συντεταγμένες θέσης των σημείων της χορδής, τα οποία βρίσκονται στον αρνητικό
ημιάξονα, σε απόσταση μικρότερη από 2 𝑚 από την αρχή των αξόνων Ο και τη χρονική στιγμή 𝑡 = 1 𝑠,
έχουν απομάκρυνση 𝑦 = −5 𝑐𝑚.                Μονάδες 6

Θέμα Δ     25722

4.1.     Τ/2 =  5s / 20 =>  T = 0,5 s        f = 1/T = 2 Hz         ω = 2π/Τ = 4π rad/s           A = s/4 = 0,2m / 4 = 0,05 m  

    y(t) = 0,05 ημ(4πt)          v = λ f  =>  λ = v / f  =  2 m/s / 2 Hz  => λ = 1 m      

    y(x,t) = A ημ(2πft + 2πx/λ)  =>  y(x,t) = 0,05 ημ(4πt + 2πx)       

4.2.      t = |x_M| / v  =  1 m / 2 m/s  =  0,5 s  = T             y_M ( x=-1 , t=13/24 ) = 0,05 ημ(4π 13/24 + 2π(-1))  =  0,05 ημ(13π /6 - 2π)  = 0,05 ημ(2π + π /6 - 2π)  = 0,05 ημ(π /6)  =  0,05  ½  =  0,025 m  

4.3.       φ(x, t) = 4πt + 2πx   =>    φ(x, t=2s) = 4π 2 + 2πx  =  8π + 2πx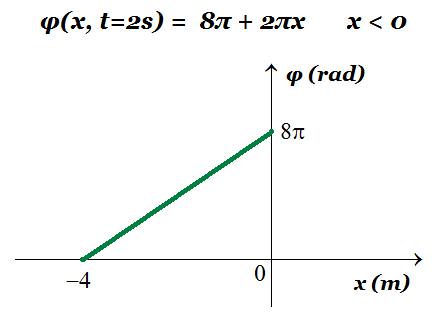              

4.4.      - 2 m  <  x  <  0      

    y(x,t) = 0,05 ημ(4πt + 2πx)  =>   y(x, t=1s)  =  0,05 ημ(4π 1 + 2πx)  =>   - 0,05 m  =  0,05 ημ(4π 1 + 2πx)  =>  

  =>  - 1  =  ημ(4π + 2πx)  =>   - 1  =  ημ(2πx)  =>   2πx  =  2Νπ  +  3π/2   =>   x  =  Ν  +  3/4  

   - 2 m  <  x  <  0   =>  - 2  <  Ν  +  3/4  <  0    =>  - 2 - 3/4  <  Ν  < - 3/4   =>  Ν = -2 , -1   

  Ν = -2  τότε  x  =  Ν  +  3/4 = -2 + 3/4  =  - 1,25 m               Ν = -1  τότε  x  =  Ν  +  3/4 = -1 + 3/4  =  - 0,25 m

ΘΕΜΑ 4
Ιδανικό ελατήριο σταθεράς k = 100 N/m  και φυσικού μήκους (Φ.Μ.)  l₀ = 1,2m, κρέμεται από οροφή. Στο ελεύθερο άκρο του ελατηρίου που βρίσκεται στο φυσικό του μήκος, κρεμάμε σώμα αμελητέων διαστάσεων, μάζας Μ = 2,5 kg και την χρονική στιγμή t₀ = 0 αφήνουμε το σύστημα ελεύθερο. Το σώμα εκτελεί απλή αρμονική ταλάντωση.   Θεωρούμε θετική φορά προς τα πάνω.

4.1.   Να προσδιορίσετε την χρονική εξίσωση της ταχύτητας του ταλαντωτή  και  την εξίσωση της δύναμης ελατηρίου που δέχεται ο ταλαντωτής συναρτήσει της απομάκρυνσής του.    Μονάδες 7
4.2.   Στο κάτω μέρος του σώματος που ταλαντώνεται, υπάρχει πολύ μικρή ακίδα, αμελητέας μάζας, ενώ χαμηλότερα υπάρχει δοχείο με νερό που ηρεμεί.  Πόση πρέπει να είναι η απόσταση της ελεύθερης επιφάνειας του υγρού από την οροφή, ώστε η ακίδα μόλις να την αγγίζει και να δημιουργεί κύματα στην επιφάνεια του υγρού;      Μονάδες 4
4.3.   Να υπολογίσετε το μήκος κύματος  λ του κύματος που διαδίδεται στην επιφάνεια του υγρού, αν γνωρίζουμε ότι από την στιγμή που αφήσαμε ελεύθερο το σύστημα να ταλαντωθεί, το κύμα έφτασε σε ένα σημείο M στην επιφάνεια του υγρού που απέχει από την πηγή του x_M = 1,5m σε χρόνο t_M = 5,5s.      Μονάδες 7
4.4.   Να υπολογίσετε την απόλυτη τιμή της διαφοράς φάσης δύο σημείων της επιφάνειας του υγρού που απέχουν απόσταση |Δx_ΑΒ| = 1,2m  και  είναι συνευθειακά με την πηγή του κύματος.       Μονάδες 7          π² = 10     

Θέμα #25986

4.1.    k = m ω²  =>  100 N/m  = 2,5 kg  ω²  =>  ω² = 40  =>  4π² / Τ²  = 40  =>  Τ = 1 s         ω = 2π/Τ  = 2π rad/s  

  M g = k Δl  =>  Δl = 2,5 10 / 100 = 0,25 m  = A           χ(t) =  0,25 ημ(2πt + π/2)           υ(t) =  0,5π συν(2πt + π/2)

     α(t) = - π² ημ(2πt + π/2) = - 10 ημ(2πt + π/2)          

   ΣF(t)  =  M a(t)  =  - 2,5 10 ημ(2πt + π/2)  =  - 25 ημ(2πt + π/2)  =  - 100 χ(t)     - 0,25 m  < χ < + 0,25 m

   ΣF(t)  = F_ελατ  -  M g  =>   - 25 ημ(2πt + π/2)  = F_ελατ  -  25  =>   F_ελατ (t)  =  25  - 25 ημ(2πt + π/2)  =  25  -  100 χ(t)     

4.2.   d  =  l₀  +  2A  =   1,2m +  0,5m  =  1,7 m

4.3.   v  =   x_M / ( t_M - T/2 )  =  1,5 m /  (5,5s - 0,5s)  =  0,3 m/s                v = λ f  =>  λ = υ /  f  =  0,3 m      

      η εξίσωση του κύματος :    y(x,t)  =  A ημ(2πt/T + π/2  -  2πx/λ)  =>   y(x,t)  =  0,25 ημ(2πt + π/2  -  2πx/0,3) =>   y(x,t)  =  0,25 ημ(2πt + π/2  -  20πx/3)

4.4.     |Δφ| / 2π  =  |Δχ| / λ  =>    |Δφ|  =  2π  1,2 / 0,3   =>   |Δφ|  =  8π rad        

ΘΕΜΑ 4
Πηγή παραγωγής αρμονικών κυμάτων αρχίζει να ταλαντώνεται τη χρονική στιγμή t = 0 στη θέση x = 0,
με ταχύτητα προς τη θετική φορά του ημιάξονα Οy . Η εξίσωση ταλάντωσης της πηγής δίνεται από την
σχέση  y = 0,1 ημ2πt . Το παραγόμενο κύμα διαδίδεται προς τη θετική φορά του ημιάξονα Οx με ταχύτητα  υ = 0,5 m/s.
4.1.  Να υπολογίσετε τη χρονική στιγμή που θα αρχίσει να ταλαντώνεται ένα σημείο Σ του ελαστικού
μέσου το οποίο βρίσκεται στη θέση x_Σ = 2,3 m.                Μονάδες 4
4.2.  Ποια είναι η φάση της πηγής όταν το σημείο Σ φτάσει για πρώτη φορά σε ακραία θέση ταλάντωσης;              Μονάδες 6
4.3.  Να γράψετε την χρονική εξίσωση της απομάκρυνσης του σημείου Σ από την θέση ισορροπίας στο
χρονικό διάστημα t ≥ 0.                  Μονάδες 7
4.4.  Να απεικονίσετε γραφικά την φάση του σημείου Σ σε συνάρτηση με τον χρόνο t.        Μονάδες 8

Θέμα Δ     26082

  y = 10ημ2πt (t σε s και y σε cm)      Α = 0,1 m      ω = 2π rad/s      f = 1 Hz     T = 1 s       λ = υ / f  = 0,5 m   

4.1.   t = x_Σ / v  =  2,3 m / 0,5 m/s = 4,6 s         y_Σ = 0,1 ημ2π( t - x_Σ/λ )       

4.2.   t = 4,6s + T/4 = 4,6 s + 1/4 s = 4,85 s        φάση τς πηγής κυμάτων =  2πt  = 2π 4,85 = 9,7π rad

4.3.   y_Σ = 0,1 ημ2π( t - x_Σ/λ )  =  0,1 ημ2π( t - 2,3 / 0,5 ) = 0,1 ημ2π( t - 4,6 )    t > 4,6s      0 < t < 4,6s : y_Σ = 0            

4.4.   φ_Σ  =  2π( t - 4,6 )    t > 4,6s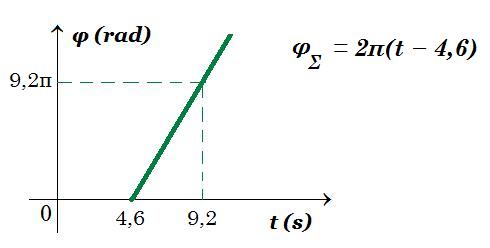 

ΘΕΜΑ 4
Κατά μήκος ενός γραμμικού, ομογενούς, ελαστικού μέσου διαδίδεται στη θετική κατεύθυνση του άξονα x'Οx ένα αρμονικό κύμα. Το σημείο O της θέσης 𝑥_𝑂 = 0 εκτελεί αρμονική ταλάντωση που περιγράφεται από την εξίσωση  y = 0,5 ημωt (S.I.).  Στο διάγραμμα φαίνεται η γραφική παράσταση της φάσης 𝜑_𝛴 του σημείου Σ του ελαστικού μέσου που βρίσκεται στη θέση 𝑥_𝛴 = 8𝑚, συναρτήσει του χρόνο υ.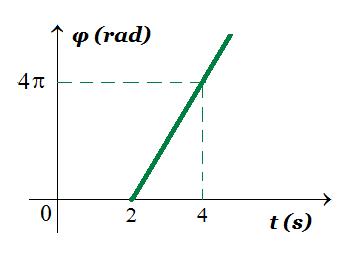

4.1.  Να υπολογίσετε το μήκος κύματος, την περίοδο και την ταχύτητα διάδοσης του κύματος.     Μονάδες 8
4.2.  Να γράψετε την εξίσωση του αρμονικού κύματος και να παραστήσετε γραφικά σε βαθμολογημένους άξονες το στιγμιότυπό του τη χρονική στιγμή 𝑡₁ = 2,5𝑠.   Μονάδες 8
4.3.  Να υπολογίσετε την ταχύτητα ταλάντωσης του σημείου Σ τη χρονική στιγμή 𝑡₁.    Μονάδες 4
4.4.  Να γράψετε την εξίσωση ενός άλλου αρμονικού κύματος που πρέπει να συμβάλει με αυτό το αρμονικό κύμα για να δημιουργηθεί στάσιμο κύμα στο γραμμικό ελαστικό μέσο.      Μονάδες 5

Θέμα Δ   25641

4.1.     φ (t,x)  =  2πt/Τ  - 2πx/λ       φ_Σ (t)  =  2πt  - 4π       άρα   ω = 2π rad/s      x_Σ  =  8 m      

    φ_Σ (t , x_Σ)  =  2πt  - 2πx_Σ/λ   =  2πt  - 2π 8 /λ  =>  λ = 4 m          το σημείο Σ αρχίζει να ταλαντώνεται μετά από  t = 2s        v = x_Σ / t =  8m / 2s = 4 m/s         v = λ f  =>  f = 1 Hz     T = 1 s        

4.2.     y(x,t)  =  A ημ(2πt/T   -  2πx/λ)  =>   y(x,t)  =  0,5 ημ(2πt  -  2πx/4) =>   y(x,t)  =  0,5 ημ(2πt  -  πx/2)          

   y(x, t=2,5s)  =  0,5 ημ(2π 2,5 - πx/2) =  0,5 ημ(5π - πx/2) =  0,5 ημ(πx/2)         t₁  =  2,5s = 1s + 1s + 0,5s = 2T + T/2

4.3.    υ(x,t)  =  π συν(2πt  -  πx/2)    =>   υ ( x=8m , t=2,5s )  =  π συν(2π 2,5  -  π 8/2)  =    π συν(5π  -  4π)  =  π συν(π)  =  - π m/s    

4.4.    y(x,t)  =  0,5 ημ(2πt  +  πx/2)

ΘΕΜΑ 4
Κατά μήκος μιας χορδής μεγάλου μήκους, η οποία ταυτίζεται με τον άξονα 𝑥'𝑂𝑥, διαδίδονται ταυτόχρονα δύο αρμονικά κύματα που έχουν εξισώσεις 
𝑦₁ = 0,2𝜂𝜇2𝜋(10𝑡 − 5𝑥) (𝑆.𝐼. ) και 𝑦₂ = 0,2𝜂𝜇2𝜋(10𝑡 + 5𝑥) (𝑆.𝐼. )
Τα δύο κύματα συμβάλλουν δημιουργώντας στο ελαστικό μέσο στάσιμο κύμα.
4.1.   Να γράψετε την εξίσωση του στάσιμου κύματος που δημιουργείται στη χορδή.     Μονάδες 6
4.2.   Να αποδείξετε ότι στην αρχή 𝑂(𝑥 = 0) του άξονα δημιουργείται κοιλία.     Μονάδες 6
4.3.   Να διερευνήσετε αν στο σημείο 𝐵(𝑥_𝐵 = 0,25 𝑚) σχηματίζεται δεσμός ή κοιλία.     Μονάδες 6
4.4.   Να υπολογίσετε το πλάτος της ταλάντωσης καθώς και τη μέγιστη ταχύτητα ταλάντωσης του υλικού σημείου Μ της χορδής που έχει τετμημένη 𝑥_𝑀 = 0,025 𝑚.     Μονάδες 7

Θέμα Δ   25721

   y(x , t)  =  0,4  συν(10πx)  ημ(20πt)        υ(x , t)  =  8π  συν(10πx)  συν(20πt)

    y(x=0 , t)  =  0,4 συν(0) ημ(20πt)   =  0,4 ημ(20πt)      A'  = 0,4 συν(10πx) = 0,4 συν(0)  =  0,4 m   κοιλία  όταν x=0

  y(x=0,25m , t)  =  0,4 συν(10π 0,25) ημ(20πt) =  0,4 συν(5π/2) ημ(20πt)  =  0    το σημείο Β είναι δεσμός 

  y(x=0,025m , t)  =  0,4 συν(10π 0,025) ημ(20πt) =  0,4 συν(π/4) ημ(20πt)  =  0,2Φ2  ημ(20πt)

 υ(x=0,025 , t)  =  8π  συν(10π 0,025)  συν(20πt) =  8π  συν(π/4)  συν(20πt) =  4πΦ2  συν(20πt)  

ΘΕΜΑ 4
Το σημείο Ο ενός γραμμικού ελαστικού μέσου αποτελεί πηγή αρμονικής διαταραχής και αρχίζει να ταλαντώνεται τη χρονική στιγμή 𝑡₀ = 0 σύμφωνα με την εξίσωση:
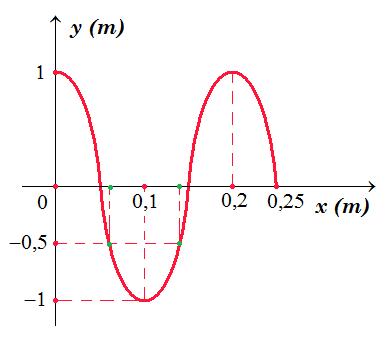
𝑦 = 𝐴 ∙ 𝜂𝜇10𝜋𝑡 (𝑆𝐼)             Το στιγμιότυπο του κύματος που διαδίδεται στο γραμμικό ελαστικό μέσο, τη χρονική στιγμή 𝑡₁ φαίνεται στο παρακάτω διάγραμμα.    

4.1.  Να υπολογίσετε το μήκος κύματος και το μέτρο της ταχύτητας διάδοσης του κύματος.        Μονάδες 6
4.2.  Να υπολογίσετε τη διαφορά φάσης των σημείων Β και Γ τη χρονική στιγμή 𝑡₁. Να εξηγήσετε αν η διαφορά φάσης των σημείων Β και Γ εξαρτάται από τη χρονική στιγμή υπολογισμού της.            Μονάδες 6
4.3.  Να παραστήσετε γραφικά σε σύστημα ορθογώνιων βαθμολογημένων αξόνων την απομάκρυνση από τη θέση ισορροπίας του σημείου Β συναρτήσει του χρόνου μέχρι τη χρονική στιγμή 𝑡 =0,5𝑠.        Μονάδες 6
Σε ένα όμοιο γραμμικό ελαστικό μέσο μήκους 𝐿, ένα αρμονικό κύμα πλάτους 𝛢 και συχνότητας   𝑓 = 5𝐻𝑧 που διαδίδεται κατά τη θετική φορά, συμβάλει με ένα αρμονικό κύμα ίδιου πλάτους  και συχνότητας που διαδίδεται κατά την αντίθετη φορά. Τη χρονική στιγμή 𝑡₀ = 0 αποκαθίσταται στάσιμο κύμα στο γραμμικό ελαστικό μέσο. Το στιγμιότυπο του στάσιμου κύματος τη χρονική στιγμή 𝑡₂ = 0,85𝑠, κατά την οποία όλα τα σημεία του γραμμικού ελαστικού μέσου έχουν μηδενική ταχύτητα φαίνεται στο παρακάτω διάγραμμα.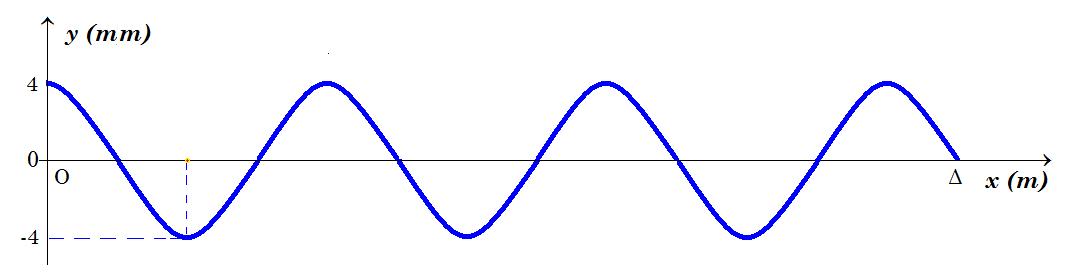
4.4.  Να γράψετε την εξίσωση του στάσιμου κύματος και να σχεδιάσετε το στιγμιότυπο του σε σύστημα ορθογώνιων βαθμολογημένων αξόνων τη χρονική στιγμή 𝑡₃ = 0,95𝑠.
Μονάδες 7

Θέμα Δ    24457

4.1.   0,75 m  =  3λ/4  =>  λ = 1 m       f = 5 Hz    T = 0,2 s        A = 2 mm = 0,002 m       v = λ f  =  5 m/s    

4.2.   φ (t,x_Β )  =  2πt/Τ  - 2πx_Β /λ       φ (t,x_Γ )  =  2πt/Τ  - 2πx_Γ /λ         φ (t,x_Β )  -  φ (t,x_Γ )  =  2πt/Τ  - 2πx_Β /λ  -  2πt/Τ  + 2πx_Γ /λ   = 2πx_Γ /λ  - 2πx_Β /λ  =  2π ( x_Γ - x_Β ) /λ  =  2π  7λ/4 / λ  =>  Δφ = 7π/2 rad  

  Δφ / 2π  =  Δχ / λ  =  7λ/4 / λ  =  7/4   =>  Δφ = 7π/2 rad       δεν  εξαρτάται από τη χρονική στιγμή υπολογισμού της

4.3.    y(x_Β=1,25m , t)  =  0,002  ημ(2πt/0,2   -   2π 1,25/1)  =  0,002  ημ(10πt  -  5π/2)   =  - 0,002  συν(10πt)        

                      10πt  -  5π/2 > 0  =>  t >  5/20 s    ή     0,25 s  £  t  £  0,5 s    το κύμα φθάνει στο σημείο Β την στιγμή  t = x_B / v =  1,25m / 5m/s  =  0,25 s

  y(x_Β=1,25m , t=0,5s)  =  0,002  ημ(2π  0,5/0,2   -   2π 1,25/1) =  0,002  ημ(5π  -  5π/2)   =  0,002  ημ(5π/2)  =  0,002 m  

4.4.   λ = 1 m       λ/4  =  1/4 m  =  0,25 m          L  =  13 λ/4   =>  L = 13/4 m    

     0,85 s  =   4  0,2  + 0,05  =  4 T  +  T/4          0,95 s  =   4  0,2  +  0,1  +  0,5  =  4 T   +  T/2  +  T/4    

     y₁ (x , t)  =  0,002  ημ(2πt/0,2   -   2π x/1)  =  0,002  ημ(10πt  -  2πx)         y₂ (x , t)  = 0,002  ημ(10πt  +  2πx)                      y (x , t)  =  0,002  συν(2πx)  ημ(10πt)    εξίσωση στασίμου κύματος     0 m  £  x  £  13/4 m