|

Κατά μήκος μιας ελαστικής χορδής έχει δημιουργηθεί στάσιμο κύμα. Στο άκρο Ο της χορδής που βρίσκεται στη θέση x=0 δημιουργείται κοιλία που τη χρονική στιγμή t=0 βρίσκεται στη θέση ισορροπίας της ταλάντωσής της με υ>0. Η ταχύτητα διάδοσης των τρεχόντων κυμάτων η συμβολή των οποίων δημιούργησε το στάσιμο κύμα είναι υδ=2cm/s. Η γραφική παράσταση της απομάκρυνσης ταλάντωσης με το χρόνο ενός σημείου Μ που βρίσκεται στη θέση x=3λ/8, όπου λ το μήκος κύματος των κυμάτων που συμβάλουν, φαίνεται στο διάγραμμα.
Γ1. Να αποδείξετε ότι το πλάτος Α των κυμάτων που συμβάλουν είναι Α=2cm. [Μονάδες 5]
Γ2. Να γράψετε την εξίσωση του στάσιμου κύματος. [Μονάδες 5]
Γ3. Να βρείτε πόσες φορές διέρχεται από τη Θ.Ι της ταλάντωσής του το σημείο Μ σε χρονικό διάστημα 10sec. [Μονάδες 5]
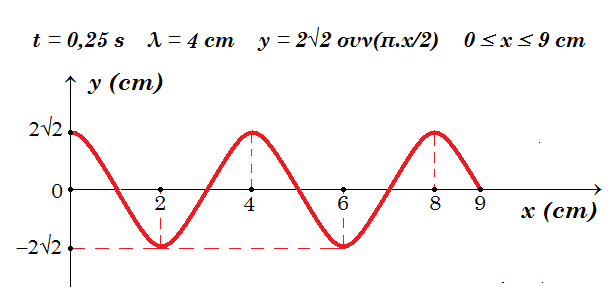
Γ4. Να γίνει το στιγμιότυπο του στάσιμου κύματος από x=0 εως x=9cm τη χρονική στιγμή t=0,25s. [Μονάδες 5]
Γ5. Να βρεθεί το μέτρο της ταχύτητας ταλάντωσης και το μέτρο της επιτάχυνσης ταλάντωσης του σημείου Μ όταν η απομάκρυνση του από τη Θ.Ι. είναι y= √2cm. [Μονάδες 5]
|
|
Γ1. T = 2 s vδ = λ/Τ => λ = vδ T = 2 cm/s 2 s = 4 cm
xM = 3λ/8 = 3/2 cm t = 3/2 cm / 2 cm/s = 3/4 s
yM = 2A συν(2π.xM /λ) ημ(2π.t/Τ) => -2√2 = 2A συν(2π.(3/2)/4) ημ(2π.(1/2)/2) =>
=> -2√2 = 2A συν(3π/4) ημ(π/2) => -2√2 = 2A (-√2/2) 1 => A = 2 cm
2A |συν(2π.xM /λ)| = |Α'| => 2A |συν(2π.(3/2) /4)| = |±2√2| =>
=> 2A |συν(3π/4)| = 2√2 => A |(-√2/2)| = √2 => Α = 2 cm
Γ2. y = A ημ2π(t/T – x/λ) => y = 2 ημ2π(t/2 – x/4) => y = 2 ημ(πt – πx/2)
Γ3. y = 5 ταλαντώσεις t / T = 10 s / 2 s
Γ4. t = 0,25 s y = 2A συν(2π.x/λ) ημ(2π.t/Τ) = 4 συν(2π.x/4) ημ(2π.0,25/2) = 4 συν(π.x/2) ημ(π/4) = 4 συν(π.x/2) √2/2 = 2√2 συν(π.x/2)
Γ5. yM = 2Α συν(2π.xM /λ) ημ(2π.t/Τ) => √2 = 4 συν(2π.(3/2)/4) ημ(2π.t/Τ) =>
=> √2 = 4 συν(3π/4) ημ(2π.t/Τ) => √2 = 4 (-√2/2) ημ(2π.t/Τ) => - 1/2 = ημ(2π.t/Τ)
συν(2π.t/Τ) = ± √3/2
vM = 2Α 2π/Τ συν(2π.xM /λ) συν(2π.t/Τ) => vM = 4 2π/2 συν(2π.(3/2)/4) (± √3/2 ) =>
=> vM = ± 4.π (±√2/2) (-√3/2) => vM = ±√6.π cm/s
aM = - 2Α (2π/Τ)2 συν(2π.xM /λ) ημ(2π.t/Τ) => αM = - 4 (2π/2)2 συν(2π.(3/2)/4) (-1/2 ) =>
=> αM = - 4 π2 (±√2/2) (-1/2) => αM = ± √2.π2 cm/s2
Κατά μήκος ενός γραμμικού ελαστικού μέσου διαδίδεται προς την θετική κατεύθυνση ένα αρμονικό κύμα, πλάτους Α=0,4m με ταχύτητα 2m/s. Την χρονική στιγμή t=0, το κύμα φτάνει στην αρχή Ο ενός προσανατολισμένου άξονα, το οποίο αρχίζει να ταλαντώνεται, κινούμενο προς τα πάνω (θετική απομάκρυνση) με περίοδο Τ=2s.
(α) Να γράψετε την εξίσωση του διαδιδόμενου κύματος.
(β) Να σχεδιάσετε ένα στιγμιότυπο του κύματος την χρονική στιγμή t1=4,5s.
(γ) Ένα υλικό σημείο Σ του μέσου, με μάζα m=1g, βρίσκεται στην θέση x1=20/3m. Να υπολογίσετε την ταχύτητα του Σ και την συνισταμένη δύναμη που δέχεται από το μέσον, τις χρονικές στιγμές t1 και t2=2,8s.
ΘΕΜΑ Δ
Ιδανικό ελατήριο σταθεράς k = 100 N/m και φυσικού μήκους (Φ.Μ.) l0 = 1,2m, κρέμεται από οροφή. Στο ελεύθερο άκρο του ελατηρίου που βρίσκεται στο φυσικό του μήκος, κρεμάμε σώμα αμελητέων διαστάσεων, μάζας Μ = 2,5 kg και την χρονική στιγμή t0 = 0 αφήνουμε το σύστημα ελεύθερο. Το σώμα εκτελεί απλή αρμονική ταλάντωση. Θεωρούμε θετική φορά προς τα πάνω.
4.1. Να προσδιορίσετε την χρονική εξίσωση της ταχύτητας του ταλαντωτή και την εξίσωση της δύναμης ελατηρίου που δέχεται ο ταλαντωτής συναρτήσει της απομάκρυνσής του.
4.2. Στο κάτω μέρος του σώματος που ταλαντώνεται, υπάρχει πολύ μικρή ακίδα, αμελητέας μάζας, ενώ χαμηλότερα υπάρχει δοχείο με νερό που ηρεμεί. Πόση πρέπει να είναι η απόσταση της ελεύθερης επιφάνειας του υγρού από την οροφή, ώστε η ακίδα μόλις να την αγγίζει και να δημιουργεί κύματα στην επιφάνεια του υγρού; Μονάδες 4
4.3. Να υπολογίσετε το μήκος κύματος λ του κύματος που διαδίδεται στην επιφάνεια του υγρού, αν γνωρίζουμε ότι από την στιγμή που αφήσαμε ελεύθερο το σύστημα να ταλαντωθεί, το κύμα έφτασε σε ένα σημείο M στην επιφάνεια του υγρού που απέχει από την πηγή του xM = 1,5m σε χρόνο tM = 5,5s.
4.4. Να υπολογίσετε την απόλυτη τιμή της διαφοράς φάσης δύο σημείων A , B της επιφάνειας του υγρού που απέχουν απόσταση |ΔxΑΒ| = 1,2m και είναι συνευθειακά με την πηγή του κύματος. π2 = 10
4.5. Κύματα δημιουργούνται και στον αέρα πάνω από την επιφάνεια του υγρού. Αν η ταχύτητα του ήχου στον αέρα είναι υηχ = 340 m/s βρείτε την απόσταση ενός πυκνώματος με το μεθεπόμενο αραίωμα.
ΘΕΜΑ Γ
Εγκάρσιο αρμονικό κύμα διαδίδεται χωρίς απώλειες ενέργειας σε γραμμικό ελαστικό μέσο (χορδή) που ταυτίζεται με τον ημιάξονα Οx, προς τη θετική κατεύθυνση. Η πηγή του κύματος βρίσκεται στο άκρο Ο (x=0) του ημιάξονα Οx του ελαστικού μέσου. Η πηγή εκτελεί απλή αρμονική ταλάντωση με εξίσωση απομάκρυνσης y=A∙ημωt.
Στοιχειώδης μάζα Δm = 10-6 kg του ελαστικού μέσου έχει ενέργεια ταλάντωσης ΕΤ = 5π2 10-7 J.
Το ελάχιστο χρονικό διάστημα για την απευθείας μετάβαση της στοιχειώδους μάζας Δm του ελαστικού μέσου από την κάτω ακραία θέση ταλάντωσής της μέχρι την επάνω ακραία θέση ταλάντωσής της είναι Δt=0,4s.
Στο ίδιο χρονικό διάστημα το κύμα έχει διαδοθεί σε απόσταση Δx=4cm.
Γ1. Να υπολογίσετε την περίοδο του κύματος, το μήκος κύματος του κύματος και το πλάτος ταλάντωσης της στοιχειώδους μάζας Δm.
Γ2. Να γράψετε την εξίσωση του αρμονικού κύματος και να σχεδιάσετε σε βαθμολογημένους άξονες το στιγμιότυπο του κύματος τη χρονική στιγμή t1=1,4s .
Γ3. Να υπολογίσετε την κινητική ενέργεια της στοιχειώδους μάζας Δm, όταν η απομάκρυνσή της από τη θέση ισορροπίας της είναι y=0,2m.
Δύο σημεία Ρ και Σ της χορδής έχουν διαφορά φάσης φΡ - φΣ = 3π/2 rad.
Γ4. Να υπολογίσετε την ταχύτητα του Σ, όταν η απομάκρυνση του σημείου Ρ από τη θέση ισορροπίας του είναι yΡ=0,4m.
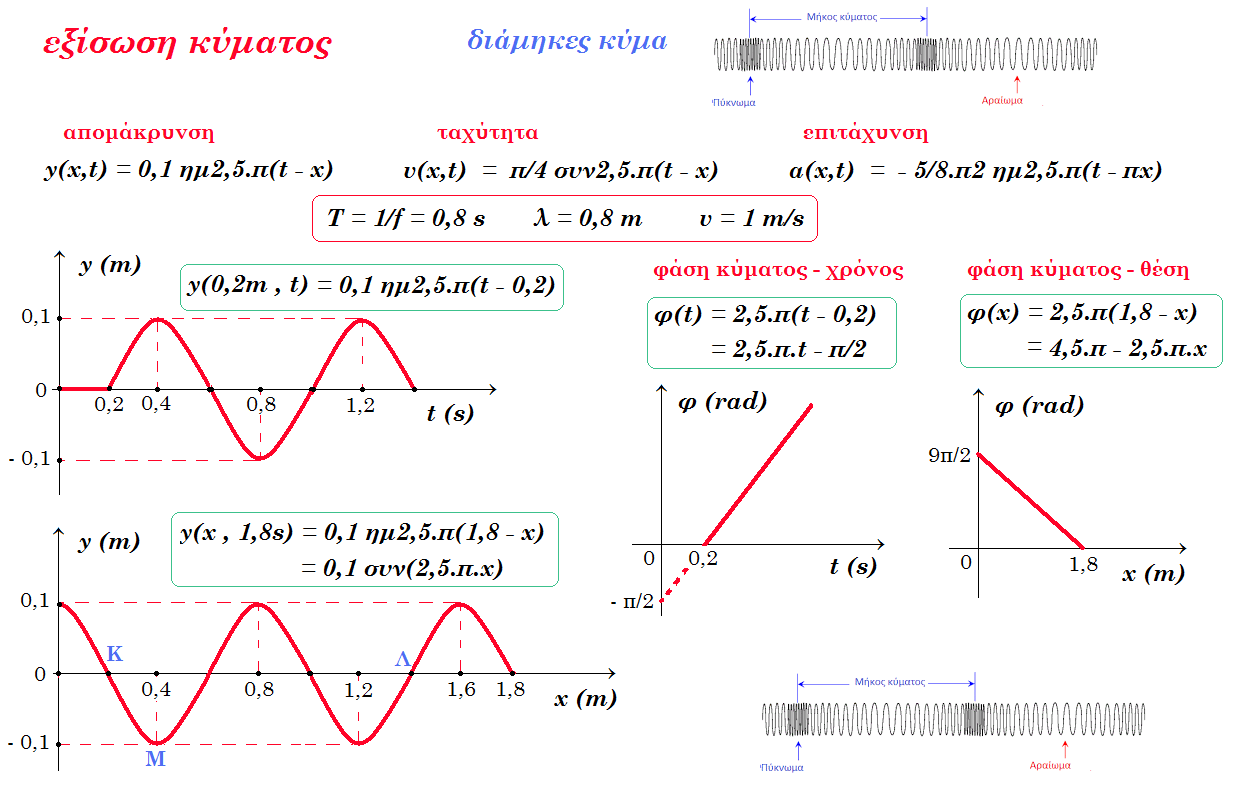
Διάμηκες αρμονικό κύμα διαδίδεται σε ελαστικό μέσο. Ένα σημείο του ελαστικού μέσου διέρχεται 10 φορές από τη θέση ισορροπίας του σε χρονικό διάστημα Δt=4s. Οι ακραίες θέσεις της ταλάντωσης κάθε σημείου απέχουν d=0,2m. Ένα πύκνωμα απέχει από το μεθεπόμενο αραίωμα απόσταση s=1,2m.
α) Να γραφεί η εξίσωση του κύματος.
β) Να γίνει η γραφική παράσταση της απομάκρυνσης ως προς τον χρόνο για ένα σημείο Κ όπου xK=0,2m.
γ) Να γίνει η γραφική παράσταση της απομάκρυνσης ως προς x τη χρονική στιγμή t1=1,8s.
δ) Σημείο Μ του ελαστικού μέσου με xΜ=0,4m έχει μεγαλύτερη φάση από την φάση του σημείου Λ κατά 5π/2. Να βρεθεί η απόσταση των σημείων Μ και Λ τη χρονική στιγμή t1=1,8s.
ε) Να γίνει η γραφική παράσταση της φάσης φ(t) για το σημείο Κ.
στ) Να γίνει η γραφική παράσταση της φάσης φ(x) τη χρονική στιγμή t1=1,8s.
Θέμα Δ #25986
4.1. k = m ω2 => 100 N/m = 2,5 kg ω2 => ω2 = 40 => 4π2 / Τ2 = 40 => Τ = 1 s ω = 2π/Τ = 2π rad/s
M g = k Δl => Δl = 2,5 10 / 100 = 0,25 m = A χ(t) = 0,25 ημ(2πt + π/2)
υ(t) = 0,5π συν(2πt + π/2) α(t) = - π2 ημ(2πt + π/2) = - 10 ημ(2πt + π/2)
ΣF(t) = M a(t) = - 2,5 10 ημ(2πt + π/2) = - 25 ημ(2πt + π/2) = - 100 χ(t) - 0,25 m < χ < + 0,25 m
ΣF(t) = Fελατ - M g => - 25 ημ(2πt + π/2) = Fελατ - 25 => Fελατ (t) = 25 - 25 ημ(2πt + π/2) = 25 - 100 χ(t)
4.2. d = l0 + 2A = 1,2m + 0,5m = 1,7 m
4.3. υ = xM / ( tM - T/2 ) = 1,5 m / (5,5s - 0,5s) = 0,3 m/s υ = λ f => λ = υ / f = 0,3 m
η εξίσωση του κύματος : y(x,t) = A ημ(2πt/T + π/2 - 2πx/λ) => y(x,t) = 0,25 ημ(2πt + π/2 - 2πx/0,3) =>
=> y(x,t) = 0,25 ημ(2πt + π/2 - 20πx/3)
4.4. |Δφ| / 2π = |Δχ| / λ => |Δφ| = 2π 1,2 / 0,3 => |Δφ| = 8π rad
4.5. υηχ = ληχ f => ληχ = υηχ / f = 340 m/s / 1 Hz => ληχ = 340 m
η απόσταση μεταξύ ενός πυκνώματος και του μεθεπόμενου αραιώματος είναι ληχ + ληχ/2 = 3/2 340 m = 510 m
(α) ω = 2π/Τ = 2π/2 = π rad/s v = λ/T => λ = v T = 2 m/s 2 s = 4 m
y(x,t) = 0,4 ημ 2π (t/2 - x/4) = 0,4 ημ(πt - πx/2) v(x,t) = 0,4π συν(πt - πx/2)
α(x,t) = 0,4π2 ημ(πt - πx/2)
(β) y = 0,4 ημ π(4,5 - x/2) = 0,4 συν(πx/2) y = 0 => x = 9 m = 2 m/s 4,5 s = v t
Τ = 2s t1 = 4,5s = 2T + T/4 δύο περίοδοι + 1/4 της περιόδου
(γ) yΣ = 0,4 ημ π(t - (20/3)/2) => yΣ = 0,4 ημ π(t - 10/3) υΣ = 0,4π συν π(t - 10/3)
αΣ = - 4 ημ π(t - 10/3) π2 = 10
ΣF = m a = 0,001 ( - 4 ημ π(t - 10/3) ) = - 0,004 ημ π(t - 10/3)
t = 20/3 m / 2 m/s = 10/3 s < 4,5 s
υΣ = 0,4π συν π(t - 10/3) = 0,4π συν π(4,5 - 10/3) = 0,4π συν(7π/6) = - 0,4π 3½/2 = - 0,2π 3½ m/s
ΣF = - 0,004 ημ π(t - 10/3) => ΣF = - 0,004 ημ(7π/6) = - 0,004 ( - ½ ) = + 0,002 Ν
την στιγμή 2,8 s το κύμα δεν έχει φθάσει στο σημείο Σ
Γ1) Δt = 0,4 s = T/2 => T = 0,8 s Δx = 0,04 m = λ/2 => λ = 0,08 m
v = λ / T = 0,08 m / 0,8 s = 0,1 m/s
ω = 2π/Τ = 2π/0,8 = 20π/8 = 5π/2 rad/s
D = Δm ω2 = 10-6 (5π/2)2 = 25/4 π2 10-6 Ν/m
ET = ½ D A2 => 5π2 10-7 = ½ 25/4 π2 10-6 A2 => A2 = 4/25 => A = 0,4 m πλάτος ταλάντωσης
Γ2) y = A ημ ( 2πt/T - 2πx/λ ) => y = 0,4 ημ ( 2πt/0,8 - 2πx/0,08 ) =>
=> y = 0,4 ημ ( 20π/8 t - 200π/8 x ) => y(t,x) = 0,4 ημ ( 2,5π t - 25π x )
t = 1,4 s = 7/4 T : y(1,4 , x) = 0,4 ημ ( 5π/2 1,4 - 25π x ) = 0,4 ημ ( 7π/2 - 25π x ) = - 0,4 συν(25π x) 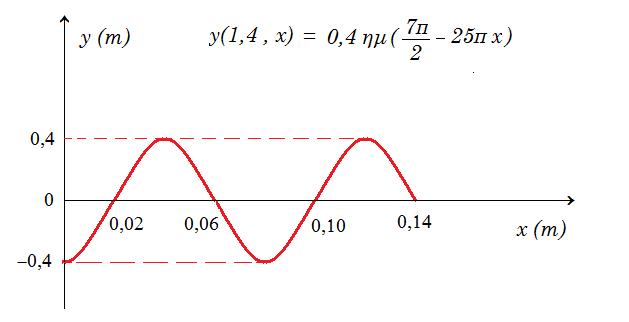
Γ3) K + U = E => K + ½ D y2 = ½ D A2 => K = ½ D A2 - ½ D y2 =>
=> Κ = ½ 25/4 π2 10-6 ( 0,42 - 0,22 ) = 25/8 π2 10-6 ( 0,16 - 0,04 ) = 0,12 25/8 π2 10-6 = 75/2 π2 10-8 J
Γ4) φΡ - φΣ = 3π/2 rad => ( 2,5π t - 25π xΡ ) - ( 2,5π t - 25π xΣ ) = 3π/2 =>
=> 25π xΣ - 25π xΡ = 3π/2 => xΣ - xΡ = 3/50 = 0,06 m
yP = 0,4 m = 0,4 ημ ( 2,5π t - 25π xP ) => ημ( 2,5π t - 25π xP ) = 1 => ημ φΡ = 1 =>
=> ημ ( 3π/2 + φΣ ) = 1 => - συν φΣ = 1 => συν φΣ = -1 => ημ φΣ = 0
yΣ (t,x) = 0,4 ημ ( 2,5π t - 25π xΣ ) = 0,4 ημ φΣ = 0,4 0 = 0
υΣ (t,x) = 0,4 2,5π συν ( 2,5π t - 25π xΣ ) = π συν φΣ = π (-1) = - π m/s
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////
διάμηκες κύμα
(α) f = 5 / 4 = 1,25 Hz T = 1/f = 0,8 s ω = 2πf = 2,5.π rad/s 2A = 0,2 m => A = 0,1 m
λ + λ/2 = 1,2 => λ = 0,8 m v = λ f = 0,8 m 5/4 Hz = 1 m/s
y(x,t) = 0,1 ημ 2π (t/0,8 - x/0,8) => y(x,t) = 0,1 ημ2,5.π(t - x)
v(x,t) = π/4 συν2,5.π(t - x) α(x,t) = - 5/8.π2 ημ2,5.π(t - πx)
(β) y(0,2m , t) = 0,1 ημ2,5.π(t - 0,2) t ³ 0,2 s
y(0,2m , t) = 0,1 ημ2,5.π(t - 0,2) = 0,1 ημ(2,5.π.t - 0,5.π) => y(0,2m , t) = - 0,1 συν(2,5.π.t)
(γ) y(x , 1,8s) = 0,1 ημ2,5.π(1,8 - x) = 0,1 ημ(4,5.π - 2,5.π.x) = 0,1 συν(2,5.π.x)
(δ) φΜ - φΛ = 5π/2 => 2,5.π(t - xΜ ) - 2,5.π(t - xΛ ) = 5π/2 => - xΜ + xΛ = 1 m =>
=> xΛ = xΜ + 1 m = 0,4 m + 1 m => xΛ = 1,4 m
y(0,4m , 1,8) = 0,1 ημ2,5.π(1,8 - 0,4) = 0,1 ημ(2,5.π.1,4) = 0,1 ημ(3π + π/2)) = - 0,1 m
y(1,4m , 1,8) = 0,1 ημ2,5.π(1,8 - 1,4) = 0,1 ημ(2,5.π.0,4) = 0,1 ημ(π) = 0
επειδή το κύμα είναι διάμηκες τη στιγμή t = 1,8 s το σημείο Λ βρίσκεται στη θέση ισορροπίας του και το σημείο Μ σε απομάκρυνση - 0,1 m οπότε η απόστασή τους είναι 1 m + 0,1 m = 1,1 m
(ε) y(0,2m , t) = 0,1 ημ2,5.π(t - 0,2) φ(t) = 2,5.π(t - 0,2) = 2,5.π.t - π/2
(στ) y(x , 1,8s) = 0,1 ημ2,5.π(1,8 - x) φ(x) = 2,5.π(1,8 - x) = 4,5.π - 2,5.π.x