
Κατά μήκος ενός γραμμικού ελαστικού μέσου, διαδίδεται ένα εγκάρσιο αρμονικό κύμα, το οποίο τη στιγμή t0=0 φτάνει σε ένα σημείο Ο, το οποίο παίρνουμε ως αρχή ενός προσανατολισμένου άξονα xx΄, με την προς τα δεξιά κατεύθυνση θετική. Το κύμα αυτό περιγράφεται από την εξίσωση:
y1=0,2∙ημ(2πt-πx) (S.Ι.)
i) Να υπολογιστούν η ταχύτητα και το μήκος κύματος, για το κύμα αυτό.
ii) Να βρεθεί η ταχύτητα ταλάντωσης ενός σημείου Σ, στη θέση x=-1m σε συνάρτηση με το χρόνο, εξαιτίας του κύματος αυτού. Ποια η ταχύτητα του Σ τη στιγμή t1=2s;
Στο ίδιο μέσο διαδίδεται ένα δεύτερο κύμα προς τα αριστερά και την στιγμή t0, έχει φτάσει στο σημείο Β. Από την συμβολή των δύο κυμάτων δημιουργείται ένα στάσιμο κύμα, ενώ τη στιγμή t1=2s έχει δημιουργηθεί στάσιμο κύμα στην περιοχή -1 ≤ x ≤ 4m, με δεσμό στη θέση x=-1m.
iii) Να βρεθεί η θέση του σημείου Β, καθώς και η εξίσωση του 2ου κύματος, το οποίο διαδίδεται προς τα αριστερά.
iv) Ποια η εξίσωση του στάσιμου κύματος, που δημιουργείται από την συμβολή των δύο παραπάνω κυμάτων.
v) Να σχεδιάσετε την μορφή μιας περιοχής του μέσου με -3m ≤ x ≤ 5m, τη χρονική στιγμή t1.
T = 1 s λ = 2 m υ = 2 m/s yΣ (x=-1m , t) = 0,2 ημ(2πt - π(-1)) = 0,2 ημ(2πt + π) = - 0,2 ημ(2πt)
vΣ (x=-1m , t) = 0,4.π συν(2πt + π) = - 0,4.π συν(2πt)
vΣ (x=-1m , t=2s) = 0,4.π συν(2π.2 + π) = - 0,4.π m/s
y(x , t) = 0,2 ημ(2πt - πx) + 0,2 ημ(2πt + πx + π) => y(x , t) = 0,4 συν(- πx - π/2) ημ(2πt + π/2) =>
=> y(x , t) = 0,4 ημ(- πx) συν(2πt) => y(x , t) = - 0,4 ημ(πx) συν(2πt)
θέση δεσμών : ημ(πx) = 0 => π.x = Ν.π => x = Ν
-1 ≤ x ≤ 4m => -1 ≤ Ν ≤ 4 => Ν = -1, 0, 1, 2, 3, 4
y(x , t) = 0,2 ημ(2πt - πx) + 0,2 ημ(2πt + πx - π) => y(x , t) = 0,4 συν(- πx + π/2) ημ(2πt - π/2) =>
=> y(x , t) = - 0,4 ημ(- πx) [ - συν(2πt) ] => y(x , t) = - 0,4 ημ(πx) συν(2πt)
yΣ (x=-1m , t=2s) = - 0,4 ημ(π.(-1)) συν(2π.2) = 0
Σε ένα σημείο Ο, στην ελεύθερη επιφάνεια νερού που ηρεμεί, πέφτουν με σταθερό ρυθμό 90 σταγόνες το λεπτό. Δημιουργείται έτσι ένα εγκάρσιο, επιφανειακό, αρμονικό κύμα. Κάποια χρονική στιγμή παρατηρούμε ότι κατά μήκος μιας ακτίνας διάδοσης Οx του κύματος σχηματίζονται 7 διαδοχικά μέγιστα (όρη), τα οποία καλύπτουν απόσταση d = 3,0 m. Θεωρούμε ότι τη χρονική στιγμή t = 0 αρχίζει η διάδοση του κύματος από τη θέση x = 0.
(α) Να υπολογίσετε την ταχύτητα διάδοσης του κύματος.
(β) Ένα μικρό κομμάτι φελλού επιπλέει σε σημείο Σ, το οποίο βρίσκεται στην ακτίνα διάδοσης Οx του κύματος στη θέση x1 = 12 m, και ταλαντώνεται με πλάτος y0 = 2 cm. Να υπολογίσετε τη μετατόπιση του φελλού, από τη θέση ισορροπίας του, τη χρονική στιγμή t1 = 17 s.
f = N/t = 90 / 60s => f = 1,5 Hz ω = 2πf = 2π 1,5 = 3π rad/s
d = 6 λ => 3m = 6λ => λ = 0,5 m v = λ f = 0,5m 1,5Hz = 0,75 m/s
το κύμα φθάνει στον φελλό μετά από χρόνο t = x/v = 12m / 0,75m/s = 16 s άρα ταλαντώνεται για χρονικό διάστημα 17 - 16 = 1 s
y = y0 ημ(ωt - 2πx/λ) = 0,02 ημ(3π 1 - 2π 12/0,3) = 0,02 ημ(3π - 80π) = 0,02 ημ(- 77π) = 0
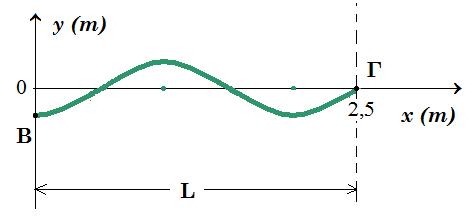
Κατά μήκος ενός γραμμικού ελαστικού μέσου, διαδίδεται ένα αρμονικό κύμα, προς την θετική κατεύθυνση (προς τα δεξιά) με πλάτος Α=0,2m με συχνότητα f=1Ηz και στο σχήμα δίνεται η μορφή ενός τμήματος ΒΓ του μέσου, μια στιγμή την οποία θεωρούμε ως αρχή μέτρησης του χρόνου (t0=0), όπου L=2,5m. Τη στιγμή αυτή η ταχύτητα ταλάντωσης του σημείου Β είναι μηδενική.
L = 5λ/4 = 2,5 m => λ = 2 m v = λ f = 2 m 1 Hz = 2 m/s ω = 2πf = 2π 1Hz = 2π rad/s f = 1 Hz => T = 1 s
y(x,t) = A ημ(2πt/T + 2πx/λ + φ) = 0,2 ημ(2πt + 2πx/2 + φ) = 0,2 ημ(2πt + πx + φ)
y(x,t=0) = - 0,2 συν(πx) = 0,2 ημ(πx + 3π/2) άρα y(x,t) = 0,2 ημ(2πt + πx + 3π/2)
υ(x,t) = 0,4π συν(2πt + πx + 3π/2) α(x,t) = - 0,8π2 ημ(2πt + πx + 3π/2)
2,25 s = 2 s + 0,25 s = T + T/4
y(x , t=2,25s) = 0,2 ημ(2π 2,25 + πx + 3π/2) = 0,2 ημ(4,5π + πx + 3π/2) = 0,2 ημ(πx)

ΘΕΜΑ Δ
Hλεκτρομαγνήτης είναι συνδεδεμένος με εναλλασσόμενη αρμονική τάση. Τη χρονική στιγμή t=0 κλείνουμε το διακόπτη που συνδέει την εναλλασσόμενη τάση με τον ηλεκτρομαγνήτη, οπότε αυτός έλκοντας περιοδικά ένα χαλύβδινο έλασμα συνδεδεμένο στο άκρο Ο χορδής μεγάλου μήκους, δημιουργεί κατά μήκος της τρέχον εγκάρσιο αρμονικό κύμα. Τη χρονική στιγμή t=0s, το σημείο Ο της χορδής αρχίζει να κινείται προς τον ηλεκτρομαγνήτη. Τη φορά κίνησης προς τα κάτω να την θεωρήσετε ως θετική φορά. Το δημιουργούμενο κύμα έχει συχνότητα 10Ηz, πλάτος 0,5cm και 3 διαδοχικές κορυφές του (όρη) καλύπτουν απόσταση 0,2 m. Η χορδή βρίσκεται πάνω σε λείο οριζόντιο δάπεδο και η ταλάντωσή της γίνεται πάνω σε αυτό.
Δ1. Να βρείτε την ταχύτητα διάδοσης του κύματος. (Μονάδες 5)
Δ2. Να γράψετε τις εξισώσεις απομάκρυνσης και ταχύτητας ταλάντωσης των σημείων της χορδής με σημείο αναφοράς το Ο(0,0). (Μονάδες 5)
Δ3. Να βρείτε τη δύναμη επαναφοράς που δέχεται ένα υλικό σημείο της χορδής με στοιχειώδη μάζα Δm = 10−4 kg , το οποίο βρίσκεται στη θέση Β ( xB = 7/120 m ), τη χρονική
στιγμή που το Ο βρίσκεται στη θέση μέγιστης θετικής απομάκρυνσής του. (Μονάδες 5)
Δ4. Να βρείτε πόσα σημεία της χορδής στο τμήμα ΟΖ=0,5m , έχουν μέτρο ταχύτητας ταλάντωσης π/20 m/s, τη χρονική στιγμή που το σημείο Ο βρίσκεται στη μέγιστη θετική
απομάκρυνσή του για τέταρτη φορά. (Μονάδες 5)
Δ1. 2λ = 0,2m => λ = 0,1m v = λ f = 0,1m 10Hz = 1 m/s T = 1/f = 0,1 s
Δ2. y = 0,005 ημ2π(10t - x/0,1) = 0,005 ημ2π(10t - 10x) => y = 0,005 ημ20π(t - x) v = 0,1π ημ20π(t - x)
α = - 2π2 ημ20π(t - x)
Δ3. t = N T + Τ/4 = N 0,1s + 0,1/4 s όπου N = 0, 1, 2, ... xB = 7/120 m
ΣF = m a = - 2π2 ημ20π(N 0,1 + 0,1/4 - 7/120) 10-4 = - 0,002 ημ (2πN + π/2 - 7π/6) =
= - 0,002 ημ (π/2 - π - π/6) = - 0,002 ημ ( - π/2 - π/6) = 0,001 Φ3 Ν
Δ4. t = 3 T + Τ/4 = 3 0,1s + 0,1/4 s
v = 0,1π ημ20π(t - x) => ± π/20 = 0,1π ημ20π(3 0,1s + 0,1/4 s - x) => ± 0,5 = ημ (2π 3 + π /2 - 20πx) =>
=> ημ (π /2 - 20πx) = ± 0,5 = ημ(π/6) => π /2 - 20πx = 2Νπ + π/6 ή π /2 - 20πx = 2Νπ + π - π/6 ή π /2 - 20πx = 2Νπ + π + π/6 ή π /2 - 20πx = 2Νπ - π/6
π /2 - 20πx = 2Νπ + π/6 => - 20πx = 2Νπ + π/6 - π /2 => - 20πx = 2Νπ - π /3 => - x = Ν/10 - 1 /60 =>
=> x = - Ν/10 + 1 /60
0 < x < 0,5m => 0 < - Ν/10 + 1 /60 < 0,5m => 0 < - Ν + 1 /6 < 5 => - 1 /6 < - Ν < 5 - 1 /6 =>
=> 1 /6 > Ν > - 5 + 1 /6 => N = -4 , -3 , -2 , -1 , 0
N = -4 x = - (-4)/10 + 1 /60 = 4/10 + 1 /60 = 24/60 + 1 /60 = 25/60 = 5/12 m
N = -3 x = - (-3)/10 + 1 /60 = 3/10 + 1 /60 = 18/60 + 1 /60 = 19/60 m
N = -2 x = - (-2)/10 + 1 /60 = 2/10 + 1 /60 = 12/60 + 1 /60 = 13/60 m
N = -1 x = - (-1)/10 + 1 /60 = 1/10 + 1 /60 = 6/60 + 1 /60 = 7/60 m
N = 0 x = 1 /60 m
π /2 - 20πx = 2Νπ - π/6 => - 20πx = 2Νπ - π/6 - π /2 => - 20πx = 2Νπ - 2π /3 => - x = Ν/10 - 1 /30 =>
=> x = - Ν/10 + 1 /30
0 < x < 0,5m => 0 < - Ν/10 + 1 /30 < 0,5m => 0 < - Ν + 1 /3 < 5 => - 1 /3 < - Ν < 5 - 1 /3 =>
=> 1 /3 > Ν > - 5 + 1 /3 => N = -4 , -3 , -2 , -1 , 0
N = -4 x = - (-4)/10 + 1 /30 = 4/10 + 1 /30 = 12/30 + 1 /30 = 13/30 m
N = -3 x = - (-3)/10 + 1 /30 = 3/10 + 1 /30 = 9/30 + 1 /30 = 10/30 m
N = -2 x = - (-2)/10 + 1 /30 = 2/10 + 1 /30 = 6/30 + 1 /30 = 7/30 m
N = -1 x = - (-1)/10 + 1 /30 = 1/10 + 1 /30 = 3/30 + 1 /30 = 4/30 m
N = 0 x = 1 /30 m
π /2 - 20πx = 2Νπ + π - π/6 => - 20πx = 2Νπ + π - π/6 - π /2 => - 20πx = 2Νπ + π /3 => - x = Ν/10 + 1 /60
=> x = - Ν/10 - 1 /60
0 < x < 0,5m => 0 < - Ν/10 - 1 /60 < 0,5m => 0 < - Ν - 1 /6 < 5 => 1 /6 < - Ν < 5 + 1 /6 =>
=> - 1 /6 > Ν > - 5 - 1 /6 => N = -5 , -4 , -3 , -2 , -1
N = -5 x = - (-5)/10 - 1 /60 = 5/10 - 1 /60 = 30/60 - 1 /60 = 29/60 m
N = -4 x = - (-4)/10 - 1 /60 = 4/10 - 1 /60 = 24/60 - 1 /60 = 23/60 m
N = -3 x = - (-3)/10 - 1 /60 = 3/10 - 1 /60 = 18/60 - 1 /60 = 17/60 m
N = -2 x = - (-2)/10 - 1 /60 = 2/10 - 1 /60 = 12/60 - 1 /60 = 11/60 m
N = -1 x = - (-1)/10 - 1 /60 = 1/10 - 1 /60 = 6/60 - 1 /60 = 5/60 m
π /2 - 20πx = 2Νπ + π + π/6 => - 20πx = 2Νπ + π + π/6 - π /2 => - 20πx = 2Νπ + 2π /3 => - x = Ν/10 + 1 /30
=> x = - Ν/10 - 1 /30
0 < x < 0,5m => 0 < - Ν/10 - 1 /30 < 0,5m => 0 < - Ν - 1 /3 < 5 => 1 /3 < - Ν < 5 + 1 /3 =>
=> - 1 /3 > Ν > - 5 - 1 /3 => N = -5 , -4 , -3 , -2 , -1
N = -5 x = - (-5)/10 - 1 /30 = 5/10 - 1 /30 = 15/30 - 1 /30 = 14/30 m
N = -4 x = - (-4)/10 - 1 /30 = 4/10 - 1 /30 = 12/30 - 1 /30 = 11/30 m
N = -3 x = - (-3)/10 - 1 /30 = 3/10 - 1 /30 = 9/30 - 1 /30 = 8/30 m
N = -2 x = - (-2)/10 - 1 /30 = 2/10 - 1 /30 = 6/30 - 1 /30 = 5/30 m
N = -1 x = - (-1)/10 - 1 /30 = 1/10 - 1 /30 = 3/30 - 1 /30 = 2/30 m
4 5 7 8 10 11 13 14 16 17 19 20 22 23 25 26 28 29
συν(20πx) = 0,5 = συν(π/3) => 20πx =
ΘΕΜΑ Γ
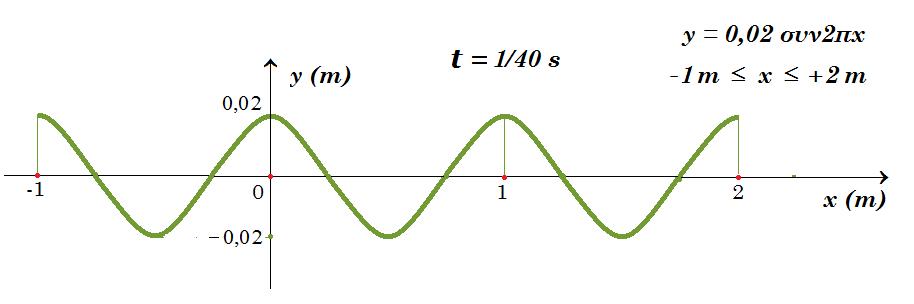
Σε ένα γραμμικό μέσο έχει δημιουργηθεί στάσιμο κύμα με εξίσωση ως προς κάποιο σημείο Ο(0,0) την: y = 0,02 ημ20πt συν2πx (S.I.)
Γ1. Να βρείτε την ταχύτητα διάδοσης του κύματος. (Μονάδες 6)
Γ2. Να γράψετε τις εξισώσεις δύο αντιθέτως διαδιδομένων κυμάτων, που η συμβολή τους θα μπορούσε να δώσει το εν λόγω στάσιμο με σημείο αναφοράς το Ο(0,0). (Μονάδες 6)
Γ3. Να σχεδιάσετε το στιγμιότυπο του κύματος τη χρονική στιγμή t = 1/40 s στην περιοχή από x=-1m έως x=+2m και να προσδιορίσετε τις θέσεις των κοιλιών και των δεσμών. (Μονάδες 6)
Γ4. Nα βρείτε την απομάκρυνση του σημείου Λ xΛ = - 5/6 m τη στιγμή που το σημείο K xΚ = 2/3 m βρίσκεται σε απομάκρυνση yΚ = 5 mm. (Μονάδες 7)
y = 0,02 ημ20πt συν2πx = 2A ημ(2πf t) συν(2πx/λ) => f = 10 Hz T = 0,1 s λ = 1 m
v = λ f = 1m 10Hz = 10 m/s
y1 = 0,01 ημ2π(10t - x) y2 = 0,01 ημ2π(10t + x)
y = 0,02 ημ(20π/40) συν2πx => y = 0,02 συν2πx - 1 m £ x £ + 2 m
yK = 0,02 ημ20πt συν2πxK => 0,005 = 0,02 ημ20πt συν(2π 2/3) => 0,005 = 0,02 ημ20πt (-1/2) =>
=> - 0,005 / 0,01 = ημ20πt => - 1/2 = ημ20πt
yΛ = 0,02 ημ20πt συν2πxΛ => yΛ = 0,02 (-1/2) συν(2π (-5/6)) = - 0,01 συν(-5π/3) => yΛ = - 0,01 1/2 = - 0,005 m
ΘΕΜΑ Γ
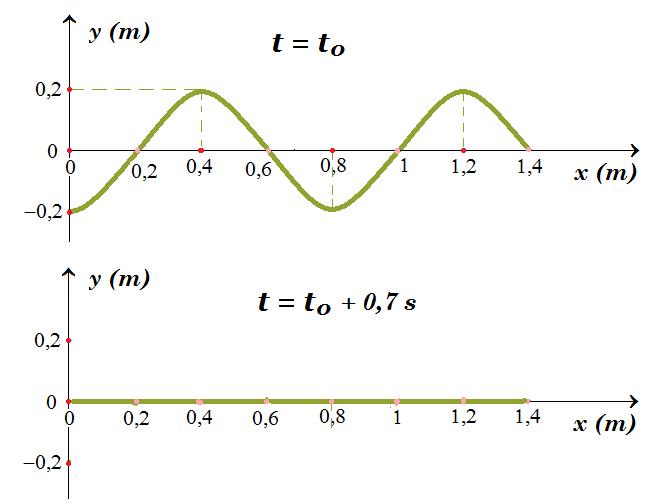
Οριζόντια χορδή ΟΒ έχει το άκρο της Β ακλόνητα στερεωμένο ενώ το μήκος του ευθυγράμμου τμήματος ΟΒ είναι (ΟΒ)=L=1,4m . Το σημείο Ο της χορδής, xO = 0, τη χρονική στιγμή t = 0, αρχίζει να ταλαντώνεται σε διεύθυνση κάθετη στη διεύθυνση της χορδής με την απομάκρυνση του σημείου Ο από τη θέση ισορροπίας του σε σχέση με το χρόνο να περιγράφεται από την συνάρτηση y = A ημ5πt (SI) . Κατά μήκος της χορδής δημιουργείται εγκάρσιο αρμονικό κύμα το οποίο διαδιδόμενο με ταχύτητα υ=2m/s , φτάνει στο ακλόνητο σημείο B και ανακλάται με αποτέλεσμα να δημιουργείται στη χορδή στάσιμο κύμα, με κοιλία στο σημείο Ο.
Στο διάγραμμα βλέπουμε την απομάκρυνση ενός σημείου Α της χορδής, σε σχέση με το χρόνο.
Γ1. Να βρείτε το μήκος κύματος των κυμάτων που δημιουργούν το στάσιμο. Μονάδες 6
Γ2. Να βρείτε τις θέσεις των σημείων της χορδής στις οποίες σχηματίζονται δεσμοί. Μονάδες 7
Γ3. Να βρείτε την οριζόντια απόσταση του σημείου Α από το άκρο Ο της χορδής, xA, καθώς και τη χρονική στιγμή . Μονάδες 6
Γ4. Να σχεδιαστεί το στιγμιότυπο του στάσιμου κύματος 0,7s μετά από κάποια χρονική στιγμή που το σημείο Ο, καθώς ταλαντώνεται με πλάτος 2Α, διέρχεται από την αρνητική ακραία θέση της ταλάντωσής του. Μονάδες 6
y(x , t) = 2A συν(2π x/λ) ημ(2π 2,5t) f = 2,5 Hz T = 0,4 s λ = υ Τ = 2 m/s 0,4 s = 0,8 m A = 0,1 m
1,4 m = 0,8 + 0,4 + 0,2 = λ + λ/2 + λ/4 κ δ κ δ κ δ κ δ
0 0,2 0,4 0,6 0,8 1 1,2 1,4
O A B
το σημείο Α αρχίζει να ταλαντώνεται τη στιγμή t1 και σταματά να ταλαντώνεται μετά από 2 περιόδους τη στιγμή t2 που σημαίνει ότι έρχεται το ανακλώμενο κύμα από το άκρο Β οπότε το σημείο Α είναι δεσμός
το κύμα από το άκρο Ο μέχρι το άκρο Β θέλει χρόνο t = 1,4m / 2m/s = 0,7 s t2 = t1 + 2T = t1 + 0,8s
η χρονική στιγμή t2 είναι όταν το ανακλώμενο κύμα φθάνει πάλι στο σημείο Α
t1 = 0,3s το κύμα σε χρόνο Τ = 0,4s φθάνει στο άκρο Β ανακλάται και σε χρόνο Τ = 0,4s φθάνει πάλι στο σημείο Α το οποίο μετά ακινητοποιείται άρα xΑ = υ t1 = 2 m/s 0,3 s = 0,6 m
y(x , t) = 2A συν(2π x/λ) ημ(2π 2,5t) => y(x , t) = 0,2 συν(2π x/0,8) ημ(2π 2,5t) 0,7s = 0,4s + 0,3s = T + 3T/4
ΘΕΜΑ Δ
Δύο πηγές εγκαρσίων κυμάτων Π1 και Π2 που βρίσκονται στην επιφάνεια υγρού, τη χρονική στιγμή t=0s αρχίζουν να εκτελούν ταυτόχρονα αρμονικές ταλαντώσεις που
περιγράφονται από την ίδια εξίσωση, y = 0,4 ημ(10πt) (SI) Για να φθάσει το κύμα της κάθε πηγής στην άλλη, χρειάζεται χρονικό διάστημα 0,7s.
Ένα σημείο της επιφάνειας του υγρού, Σ, που απέχει 4,5m από την πηγή Π1 και 7,5m από τη πηγή Π2 αρχίζει να ταλαντώνεται τη χρονική στιγμή t1 = 0,45s.
Δ1. Να βρείτε την ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού, καθώς και το μήκος κύματος. Μονάδες 4
Δ2. Να βρείτε το πλήθος των σημείων αποσβετικής συμβολής που βρίσκονται μεταξύ των δύο πηγών. Μονάδες 5
Δ3. Να σχεδιάσετε τη γραφική παράσταση της ταχύτητας ταλάντωσης του σημείου Σ σε συνάρτηση με τον χρόνο σε αριθμημένους άξονες για το χρονικό διάστημα [0 , 1s] . Μονάδες 5
Δ4. Ένα σημείο Κ της επιφάνειας του υγρού απέχει από τις πηγές Π1 και Π2 αποστάσεις rK1 = 6m και rK2 =10m . Η υπερβολή που διέρχεται από το Κ τέμνει το ευθύγραμμο τμήμα Π1Π2 στο σημείο Λ. Να βρείτε την απόσταση του σημείου Λ από την πηγή Π1. Μονάδες 5
Δ5. Να βρείτε την ελάχιστη αύξηση επί τοις % που πρέπει να προκαλέσουμε στη συχνότητα των πηγών, ώστε το σημείο Σ να αποκτήσει το μέγιστο δυνατό πλάτος. Μονάδες 6
Δ1. y = 0,4 ημ(10πt) (SI) f = 5 Hz A = 0,4 m t = 0,7 s v = ΣΠ1 / t1 = 4,5 m / 0,45 s = 10 m/s ταχύτητα κύματος λ = v / f = 10 m/s / 5 Hz = 2 m μήκος κύματος Π1Π2 = 10 m/s 0,7 s = 7 m = d απόσταση των δύο πηγών ΣΠ2 - ΣΠ1 = 7,5 m - 4,5 m = 3 m = 3/2 2 m = 3/2 λ = λ + λ/2 = Νλ + λ/2 => Ν = 1
Δ2. |r1 - r2| = Νλ + λ/2 => |r1 - (d - r1)| = Νλ + λ/2 => |2r1 - d| = Νλ + λ/2 =>
=> 2r1 - d = Νλ + λ/2 ή 2r1 - d = -Νλ - λ/2
2r1 = d + Νλ + λ/2 => r1 = d/2 + Νλ/2 + λ/4 επειδή 0 < r1 < d => 0 < d/2 + Νλ/2 + λ/4 < d =>
=> - d/2 - λ/4 < Νλ/2 < d - d/2 - λ/4 => - d - λ/2 < Νλ < d - λ/2 => - 7 - 1 < Ν 2 < 7 - 1 =>
=> - 8 < Ν 2 < 6 => - 4 < Ν < 3 => N = -4 , -3 , -2 , -1 , 0 , 1 , 2 , 3 θέσεις σημείων απόσβεσης
N = -4 r1 = d/2 + Νλ/2 + λ/4 = 7/2 + (-4) + 1/2 = 0 θέση πηγής Π1 r2 = 7 m |r1 - r2| = 7 m = 3 2m + 1m
N = -3 r1 = d/2 + Νλ/2 + λ/4 = 7/2 + (-3) + 1/2 = 1 m r2 = 6 m |r1 - r2|= 5 m = 2 2m + 1m
N = -2 r1 = d/2 + Νλ/2 + λ/4 = 7/2 + (-2) + 1/2 = 2 m r2 = 5 m |r1 - r2|= 3 m = 1 2m+ 1m
N = -1 r1 = d/2 + Νλ/2 + λ/4 = 7/2 + (-1) + 1/2 = 3 m r2 = 4 m |r1 - r2|= 1 m = 0 2m + 1m
N = 0 r1 = d/2 + Νλ/2 + λ/4 = 7/2 + 0 + 1/2 = 4 m r2 = 3 m |r1 - r2|= 1 m
N = 1 r1 = d/2 + Νλ/2 + λ/4 = 7/2 + 1 + 1/2 = 5 m r2 = 2 m |r1 - r2|= 3 m
N = 2 r1 = d/2 + Νλ/2 + λ/4 = 7/2 + 2 + 1/2 = 6 m r2 = 1 m |r1 - r2|= 5 m
N = 3 r1 = d/2 + Νλ/2 + λ/4 = 7/2 + 3 + 1/2 = 7 m θέση πηγής Π2 r2 = 0 m |r1 - r2|= 7 m
2r1 = d - Νλ - λ/2 => r1 = d/2 - Νλ/2 - λ/4 επειδή 0 < r1 < d => 0 < d/2 - Νλ/2 - λ/4 < d =>
=> - d/2 + λ/4 < - Νλ/2 < d - d/2 + λ/4 => - d + λ/2 < - Νλ < d + λ/2 => - 7 + 1 < - Ν 2 < 7 + 1 =>
=> - 6 < - Ν 2 < 8 => - 3 < - Ν < 4 => 3 > Ν > - 4 => N = -4 , -3 , -2 , -1 , 0 , 1 , 2 , 3 θέσεις σημείων απόσβεσης
Δ3. στο σημείο Σ φθάνει κύμα από την πηγή Π1 τη στιγμή t1 = 0,45s και τη στιγμή t2 = 7,5 m / 10 m/s = 0,75s φθάνει κύμα από την πηγή Π2 τα δύο κύματα συμβάλλουν από 0,75s έως 1s
Δ4. rK2 - rK1 = 10m - 6m = 4m = 2 2m = 2λ = Νλ => Ν = 2 ενισχυτική συμβολή το σημείο Λ απέχει από την πηγή Π1 1,5 m ή 5,5 m διότι :
|r1 - r2| = Νλ => |r1 - (d - r1)| = Νλ => |2r1 - d| = Νλ => 2r1 - d = Νλ ή 2r1 - d = - Νλ
2r1 = d + Νλ => r1 = d/2 + Νλ/2 επειδή 0 < r1 < d => 0 < d/2 + Νλ/2 < d =>
=> - d/2 < Νλ/2 < d - d/2 => - d < Νλ < d => - 7 < Ν 2 < 7 =>
=> - 3,5 < Ν < 3,5 => N = -3 , -2 , -1 , 0 , 1 , 2 , 3 θέσεις σημείων ενίσχυσης
N = -3 r1 = d/2 + Νλ/2 = 7/2 + (-3) = 0,5 m r2 = 6,5 m |r1 - r2|= 6 m = 3 2m
N = -2 r1 = d/2 + Νλ/2 = 7/2 + (-2) = 1,5 m r2 = 5,5 m |r1 - r2|= 4 m = 2 2m
N = -1 r1 = d/2 + Νλ/2 = 7/2 + (-1) = 2,5 m r2 = 4,5 m |r1 - r2|= 2 m = 1 2m
N = 0 r1 = d/2 + Νλ/2 = 7/2 + 0 = 3,5 m r2 = 3,5 m |r1 - r2|= 0 m
N = 1 r1 = d/2 + Νλ/2 = 7/2 + 1 = 4,5 m r2 = 2,5 m |r1 - r2|= 2 m
N = 2 r1 = d/2 + Νλ/2 = 7/2 + 2 = 5,5 m r2 = 1,5 m |r1 - r2|= 4 m = 2 2m
N = 3 r1 = d/2 + Νλ/2 = 7/2 + 3 = 6,5 m r2 = 0,5 m |r1 - r2|= 6 m
Δ4. rΣ2 - rΣ1 = 7,5m - 4,5m = 3m = Ν λ' ενισχυτική συμβολή
Ν = 0 αδύνατον Ν = 1 λ΄ = 3m αυξάνεται το μήκος κύματος άρα μειώνεται η συχνότητα
Ν = 2 λ' = 1,5m f ' = v / λ' = 10 m/s / 1,5 m = 20/3 Hz Δf / f = ( f ' - f ) / f = 20/3 / 5 - 1 = 4/3 - 1 = 1/3 ποσοστό 33,3 %
Ν = 3 λ' = 1m f ' = v / λ' = 10 m/s / 1 m = 10 Hz Δf / f = ( f ' - f ) / f = 10 / 5 - 1 = 2 - 1 = 1 άρα 100 %
Ν = 4 λ' = 0,75m Ν = 5 λ' = 0,6m
ΘΕΜΑ Γ
Αρμονικό εγκάρσιο κύμα που περιγράφεται από την εξίσωση y = 0,04 ημ2π(t - x/2) διαδίδεται σε ομογενή ελαστική χορδή κατά τη θετική κατεύθυνση του ημιάξονα Οx . Τη χρονική στιγμή t=0s, το σημείο Ο της θέσης x=0m αρχίζει να ταλαντώνεται με θετική ταχύτητα.
Γ1. Να υπολογίσετε τη συχνότητα, το μήκος κύματος και την ταχύτητα διάδοσης του κύματος. Μονάδες 6
Γ2. Για το σημείο Α της χορδής, που βρίσκεται στη θέση x=4m, να βρείτε τη χρονική στιγμή που αρχίζει να ταλαντώνεται και να γράψετε την εξίσωση της ταχύτητας σε σχέση με το χρόνο για το χρονικό διάστημα [0 , 4s] Μονάδες 6
Γ3. Αν θεωρήσουμε ότι στο σημείο Α υπάρχει στοιχειώδης μάζα 0,002 kg , να υπολογίσετε την ενέργεια ταλάντωσής της και να σχεδιάσετε σε αριθμημένους άξονες τη δυναμική ενέργεια της στοιχειώδους μάζας σε συνάρτηση με το χρόνο, για το χρονικό διάστημα [0 , 4s] Μονάδες 6
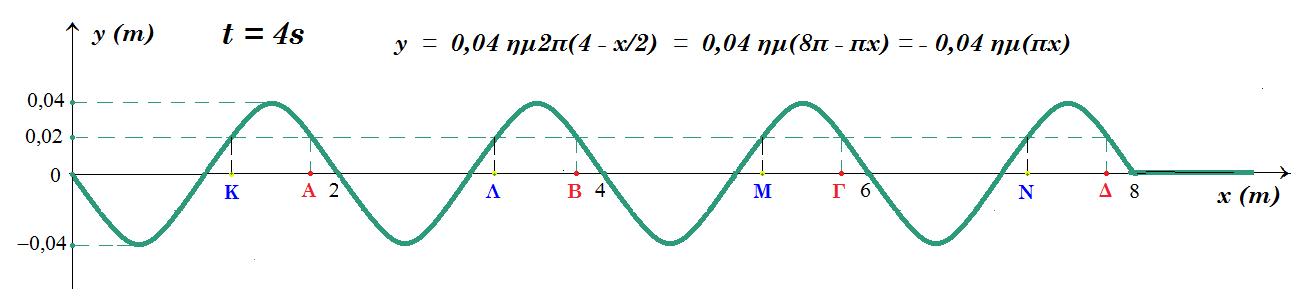
Γ4. Τη χρονική στιγμή t=4s , να βρείτε την οριζόντια απόσταση από το σημείο Ο εκείνου του σημείου το οποίο έχει απομάκρυνση 0,02 m. με θετική ταχύτητα για 1η φορά. Μονάδες 7
Γ1. y = 0,04 ημ2π(t - x/2) = Α ημ2π(t/Τ - x/λ) Τ = 1 s λ = 2 m v = λ f = 2 m/s
υ = 0,08π συν2π(t - x/2) για t=0 x=0 έχουμε υ = 0,08π συν(0) = 0,08π > 0
Γ2. t = x / v = 4m / 2m/s = 2s yA = 0,04 ημ2π(t - 4/2) = 0,04 ημ(2πt - 4π) = 0,04 ημ(2πt) 2s £ t £ 4s από 0s έως 2s το σημείο Α ηρεμεί διότι δεν έχει φθάσει το κύμα
υA (t) = 0,08 π συν(2πt - 4π) = 0,08 π συν(2πt) 2s £ t £ 4s
Γ3. Ε = ½ m ω2 Α2 = ½ 0,002 4π2 0,042 = 0,001 40 0,0016 = 64 10-6 J
U = ½ m ω2 y2 = ½ 0,002 4π2 0,042 ημ2 2π(t - x/2) = 64 10-6 ημ2 2π(t - x/2) 2s £ t £ 4s
Γ4. y = 0,02 m , t = 4s => 0,04 ημ2π(4 - x/2) = 0,02 => ημ2π(4 - x/2) = 0,5 => συν2π(4 - x/2) = +Φ3/2 > 0
υ = 0,08 π συν(8π - πx) = + 0,08π Φ3/2 = + 0,04π Φ3 m/s > 0
t = 4s x = v t = 2 m/s 4 s = 8 m x < 8m : σε χρόνο 4s το κύμα διανύει απόσταση 8 m άρα ταλαντώνονται τα σημεία της χορδής που απέχουν από το Ο απόσταση < 8 m
ημ2π(t - x/2) = 0,5 => ημ2π(4 - x/2) = 0,5 = ημ(π/6) => 2π(4 - x/2) = 2Νπ + π/6 => 8 - x = 2Ν + 1/6 =>
=> x = - 2Ν + 8 - 1/6 => 0 < x < 8m => 0 < - 2Ν + 8 - 1/6 < 8m => - 8 + 1/6 < - 2Ν < 1/6 =>
=> 4 - 1/12 > Ν > - 1/12 => Ν = 0 , 1 , 2 , 3
N = 0 x = (8 - 1/6) m = 47/6 m < 8 m για να έχει φθάσει το κύμα
Ν = 1 x = - 2 + 8 - 1/6 = 6 - 1/6 = 35/6 m
Ν = 2 x = - 4 + 8 - 1/6 = 4 - 1/6 = 23/6 m
Ν = 3 x = - 6 + 8 - 1/6 = 2 - 1/6 = 11/6 m
y = 0,04 ημ2π(4 - x/2) = 0,04 ημ(8π - πx) = - 0,04 ημ(πx)
υ = 0,08 π συν(8π - πx) = 0,08 π συν(8π - π(8 - 1/6)) = 0,08 π συν(- π/6) = + 0,08π Φ3/2 = + 0,04π Φ3 m/s > 0
υ = 0,08 π συν(8π - πx) = 0,08 π συν(8π - π(7 + 1/6)) = 0,08 π συν(π - π/6) = - 0,08π Φ3/2 = - 0,04π Φ3 m/s < 0
τα σημεία Α, Β, Γ, Δ έχουν θετική ταχύτητα την στιγμή t = 4s σε απομάκρυνση y = 0,02 m
ενώ τα σημεία Κ, Λ, Μ, Ν με x = (7 + 1/6) m , (5 + 1/6) m , (3 + 1/6) m , (1 + 1/6) m έχουν αρνητική ταχύτητα την στιγμή t = 4s σε απομάκρυνση y = 0,02 m
στο σημείο Δ φθάνει το κύμα τη στιγμή t = xΔ / v = (8 - 1/6) m / 2 m/s = 4 - 1/12 s = 47/12 s
στο σημείο Γ φθάνει το κύμα τη στιγμή t = xΓ / v = (6 - 1/6) m / 2 m/s = 3 - 1/12 s = 35/12 s
στο σημείο B φθάνει το κύμα τη στιγμή t = xB / v = (4 - 1/6) m / 2 m/s = 2 - 1/12 s = 23/12 s
στο σημείο A φθάνει το κύμα τη στιγμή t = xA / v = (2 - 1/6) m / 2 m/s = 1 - 1/12 s = 11/12 s
την στιγμή t = 4s σε απομάκρυνση y = 0,02 m το σημείο Δ έχει θετική ταχύτητα για 1η φορά
το σημείο Γ έχει θετική ταχύτητα για 2η φορά το σημείο Β έχει θετική ταχύτητα για 3η φορά
και το σημείο Α έχει θετική ταχύτητα για 4η φορά
ΘΕΜΑ Δ
Σε οριζόντια τεντωμένη χορδή μήκους L=1m που έχει τα δύο άκρα της Α, Β στερεωμένα ακλόνητα, δημιουργείται στάσιμο κύμα που περιγράφεται από την εξίσωση y = 0,02 συν5πx ημ4πt
Να υπολογίσετε:
Δ1. το πλάτος ταλάντωσης και το μήκος κύματος των αρχικών κυμάτων που δημιούργησαν το στάσιμο κύμα. Μονάδες 6
Δ2. τον αριθμό των κοιλιών και τον αριθμό δεσμών που δημιουργούνται στη χορδή. Μονάδες 6
Δ3. το πλάτος ταλάντωσης του σημείου Ν της χορδής που απέχει από το μέσον της Μ d = 1/30 m. Μονάδες 6
Δ4. την αμέσως μικρότερη συχνότητα στάσιμου που μπορεί να αποκατασταθεί στη χορδή καθώς και το νέο πλάτος ταλάντωσης που θα έχει το σημείο Ν, αν τα πλάτη των αρχικών κυμάτων που δημιούργησαν το στάσιμο κύμα παρέμειναν ίδια. Μονάδες 7
Δ1. από y = 2A συν(2πx/λ) ημ(2πt/Τ) και y = 0,02 συν5πx ημ4πt
y1 = 0,01 ημ 2π( 2t - 5x/2 ) y2 = 0,01 ημ 2π( 2t + 5x/2 )
έχουμε 2Α = 0,02 m => A = 0,1 m πλάτος ταλάντωσης των αρχικών κυμάτων 2πx/λ = 5πx => λ = 2/5 = 0,4 m , 2πt/Τ = 4πt => T = 0,5 s , f = 2 Hz v = λ f = 0,4 m 2 Hz = 0,8 m/s ταχύτητα κύματος
Δ2. τα άκρα της χορδής είναι ακλόνητα σημεία άρα δεσμοί 1 m = 0,4 m + 0,4 m + 0,2 m => L = 2 λ + λ/2 = 5λ/2
δ κ δ κ δ κ δ κ δ κ δ έξι δεσμοί , πέντε κοιλίες
Δ3. MN = 1/30 m ON = OM + MN = 1/2 m + 1/30 m = 16/30 m = 8/15 m
AN = 0,02 συν5πxN = 0,02 συν(5π 8/15) = 0,02 συν( 8π/3 ) = 0,02 συν( 6π/3 + 2π/3 ) = 0,02 ( -½ ) = - 0,01 m
MN = 1/30 m ON = OM - MN = 1/2 m - 1/30 m = 14/30 m = 7/15 m
AN = 0,02 συν5πxN = 0,02 συν(5π 7/15) = 0,02 συν( 7π/3 ) = 0,02 συν( 6π/3 + π/3 ) = 0,02 ( -½ ) = + 0,01 m
Δ4. δ κ δ κ δ κ δ κ δ πέντε δεσμοί , τέσσερις κοιλίες L = 2λ' => λ' = 0,5 m
v = λ' f ' => 0,5 m f ' = 0,8 m/s => f ' = 1,6 Hz
y = 2A συν(2πx/λ') ημ(2πf ' t) => y = 0,02 συν (2πx / 0,5) ημ (2π 1,6 t) = 0,02 συν (4πx) ημ (3,2π t)
MN = 1/30 m ON = OM + MN = 1/2 m + 1/30 m = 16/30 m = 8/15 m
AN = 0,02 συν (4πxN ) = 0,02 συν(4π 16/30) = 0,02 συν( 64π/15 30 ) = 0,02 συν( 60π/30 + 4π/30 ) =
= 0,02 συν( 4π/30 ) = 0,02 συν( π/2 - 11π/30 ) = 0,02 ημ ( 11π/30 ) = 0,02 [ 0,84 ]½ m
4π/30 = 15π/30 - 11π/30 = π/2 - 11π/30
συν (11π/30) = 0,4 => ημ (11π/30) = [ 1 - 0,42 ]½ = [ 1 - 0,16 ]½ = [ 0,84 ]½
ημα + ημβ = 2 ημ(α+β)/2 συν(α-β)/2
ημ(2πt/Τ - 3π/2) = συν(2πx/λ) συν(3π/2) + ημ(2πx/λ) ημ(3π/2) = - ημ(2πx/λ)
συν(2πx/λ - 3π/2) = συν(2πx/λ) συν(3π/2) + ημ(2πx/λ) ημ(3π/2) = - ημ(2πx/λ)
y1 = A ημ(2πt/Τ - 2πx/λ - π) y2 = A ημ(2πt/Τ + 2πx/λ + π/2 + π)
y = y1 + y2 = 2A ημ(2πx/λ + π) ημ(2πt/Τ) = - 2A ημ(2πx/λ) ημ(2πt/Τ)
2πx/λ - 3π/2 = (α - β)/2
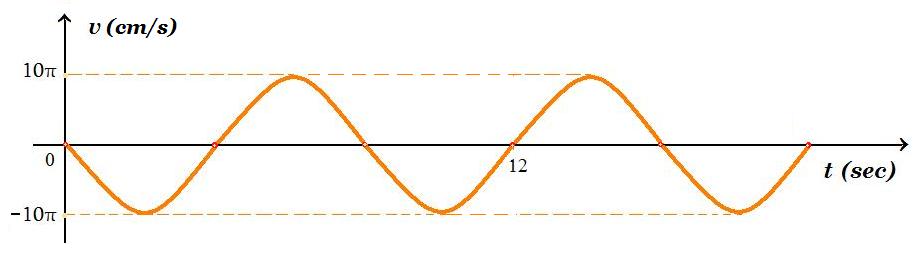
Σώμα εκτελεί Α.Α.Τ., στο σχήμα φαίνεται το διάγραμμα της ταχύτητας του σώματος συναρτήσει του χρόνου. Το σώμα βρίσκεται στην θέση Ο(0,0) επάνω στον άξονα χ'Oχ, γίνεται πηγή κυμάτων που διαδίδονται στον χώρο (ελαστικό μέσο) γύρω από το σώμα με ταχύτητα υ = 0,2 m/s.
(Α) Γράψτε την εξίσωση της απομάκρυνσης του σώματος συναρτήσει του χρόνου.
(Β) Γράψτε την εξίσωση του κύματος συναρτήσει του χρόνου t και της απόστασης x από την πηγή.
(Γ) Βρείτε την ενέργεια ταλάντωσης ενός υλικού σημείου Σ μάζας Δm = 1μg του ελαστικού μέσου που βρίσκεται στη θέση x = +2m.
(Δ) Βρείτε τον ρυθμό μεταβολής της δυναμικής ενέργειας ταλάντωσης του σημείου (Ο) συναρτήσει του χρόνου.
(Ε) Το κύμα προσπίπτει κάθετα σε επίπεδη επιφάνεια και ανακλάται χωρίς απώλεια ενέργειας. Γράψτε την εξίσωση του στάσιμου κύματος που δημιουργείται.
3Τ/2 = 12 => Τ = 8s f = 1/T = 1/8 Hz ω = 2π/Τ = 2π/8 = π/4 rad/s
v(t) = - 10π ημ(π/4 t) ( cm/s ) 10π cm/s = A π/4 rad/s => A = 40 cm = 0,4 m
v(t) = - 0,1π ημ(π/4 t) y(t) = 0,4 συν(π/4 t) = 0,4 ημ(π/4 t + π/2) α(t) = - 0,025π2 συν(π/4 t) (S.I.)
v = λ f => λ = v / f = υ Τ = 0,2 m/s 8 s => λ = 1,6 m μήκος κύματος που διαδίδεται στο μέσον
y(x,t) = Α ημ(ωt - 2πx/λ + φ0 ) = 0,4 ημ(π/4 t - 2πx/1,6 + π/2) => y(x,t) = 0,4 ημ 2π(t/8 - 5x/8 + π/2)
υ(x,t) = 0,1π συν 2π(t/8 - 5x/8 + π/2) α(x,t) = - 0,025π2 ημ 2π(t/8 - 5x/8 + π/2)
ET = ½ D Α2 => ET = ½ Δm ω2 Α2 => ET = ½ 10-9 (π/4)2 0,42 = ½ 10-9 π2/16 0,16 = ½ 10-11 π2 => ET = 5π2 10-12 J
U = ½ D y2 => U = ½ Δm ω2 y2 => U = ½ 10-9 (π/4)2 0,42 ημ2 2π(t/4 - 5x/8 + π/2) =>
=> U = 5π2 10-12 ημ2 2π(t/4 - 5x/8 + π/2)