ΘΕΜΑ 4
Στο κύκλωμα του παρακάτω σχήματος η πηγή έχει Η.Ε.Δ. ℇ = 12 V και αμελητέα εσωτερική αντίσταση, ενώ οι αντιστάτες έχουν αντίσταση R1 = 5Ω και R2 = 1Ω. Το πηνίο είναι ιδανικό και έχει συντελεστή αυτεπαγωγής L, ενώ οι αγωγοί σύνδεσης έχουν αμελητέα αντίσταση.  Αρχικά ο διακόπτης δ είναι ανοιχτός και το κύκλωμα δεν διαρρέεται από ρεύμα. Την χρονική στιγμή t₀ = 0 κλείνουμε το διακόπτη.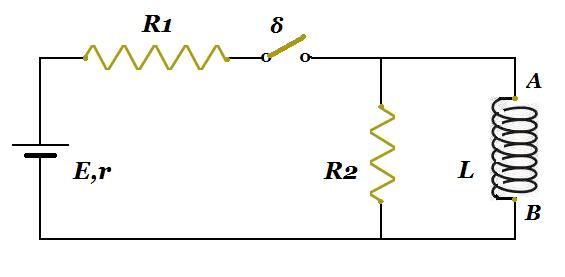 

4.1.   Να υπολογίσετε την ένταση του ηλεκτρικού ρεύματος στο κύκλωμα αμέσως μετά το κλείσιμο του διακόπτη και μετά από αρκετό χρόνο, όταν θα έχουν αποκατασταθεί οι τελικές τιμές των ρευμάτων.               Μονάδες 6
4.2.   Αφού αποκατασταθούν οι τελικές τιμές των ρευμάτων, ανοίγουμε το διακόπτη. Να καθορίσετε ποιοι κλάδοι του κυκλώματος εξακολουθούν να διαρρέονται από ρεύμα και να σχεδιάσετε τη φορά του ρεύματος.     Μονάδες 6
4.3.   Κάποια χρονική στιγμή t₁ μετά το άνοιγμα του διακόπτη, διαπιστώθηκε ότι το ρεύμα στον αντιστάτη R₂ είναι i₁ = 0,3A και το ρεύμα στο πηνίο μειώνεται με ρυθμό di/dt = −10 A/s.  Να υπολογιστεί ο συντελεστής αυτεπαγωγής του πηνίου και ο ρυθμός απώλειας ενέργειας του πηνίου την χρονική στιγμή t₁.       Μονάδες 6
4.4.   Αν το χρονικό διάστημα από τη στιγμή που ανοίγουμε το διακόπτη μέχρι να μηδενιστεί το ρεύμα στο πηνίο είναι Δt = 0,2s να υπολογίσετε τη μέση θερμική ισχύ που θα παραχθεί στους ωμικούς αντιστάτες σε αυτό το χρονικό διάστημα.         Μονάδες 7

Θέμα #28258

4.1.  αμέσως μετά το κλείσιμο του διακόπτη  το πηνίο δεν  διαρρέεται από ρεύμα  οπότε  Ι_αρχικό = E/(R₁ + R₂)  = 12V / (5Ω + 1Ω) = 2 Α    το πηνίο γίνεται πηγή με θετικό πόλο το άκρο Α  και  αρνητικό το άκρο Β

μετά από αρκετό χρόνο το πηνίο λειτουργεί ως βραχυκύκλωμα  οπότε η αντίσταση R₂ τίθεται εκτός   οπότε  Ι_τελικό  =  E / R₁  =  12V / 5Ω  = 2,4 Α  

4.2.  όταν ανοίξουμε τον διακόπτη  η πηγή  και η αντίσταση R₁ τίθενται εκτός   οπότε  ρεύμα κυκλοφορεί στον βρόχο  της αντίσταση R₂  και του πηνίου    το πηνίο γίνεται πηγή με θετικό πόλο το άκρο Β  και  αρνητικό το άκρο Α,  διαρρέεται από ρεύμα ίδιας φοράς ( κλείστος διακόπτης )

4.3.  - L di/dt = i R₂  => - L (- 10 A/s) = 0,3 A 1Ω  => L = 0,03 Henry         P_R2 = i² R₂  =  (0,3 A)² 1 Ω =  0,09 Watt   

4.4.      πριν ανοίξουμε τον διακόπτη  το πηνίο διαρρεόταν από ρεύμα εντάσεως  2,4 Α  και  είχε αποθηκευμένη ενέργεια  U = ½  L  Ι²_τελικό   = ½  0,03 H   (2,4A)²   =  0,0864 J    η αποθηκευμένη ενέργεια του πηνίου καταναλώνεται στην αντίσταση R₂   σε χρόνο 0,2 s  

   dU/dt = 0,0864 J / 0,2 s =  0,432 J/s

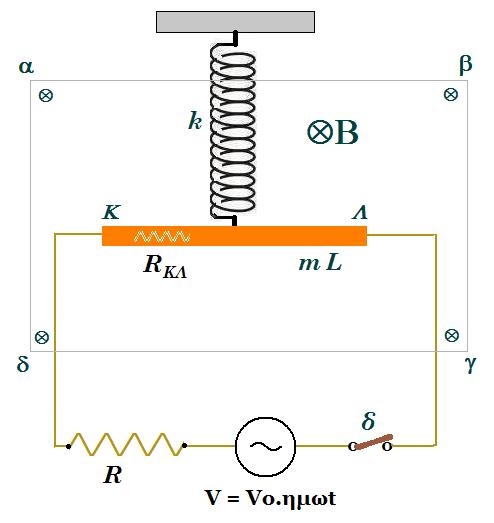 το κύκλωμα διαρρέεται από εναλλασσόμενο ρεύμα  i = I₀ ημωt  όπου  Ι₀ = V₀ / (R + R_ΚΛ)   ο αγωγός ΚΛ  δέχεται  δύναμη Laplace  F_L = B i l  =  B l I₀  ημωt    

 οπότε έχουμε   ΣF = m a   =>    F_L  +  mg  + F_ελατ  =  B l I₀  ημωt  +  mg  +  k x  =  m a    

t = 0   a = 0  =>  mg  +  k x₀  =  0 =>  x₀ = - mg / k     θετική κατεύθυνση κατακόρυφη προς τα κάτω 

ΘΕΜΑ 4
Ευθύγραμμος μεταλλικός αγωγός 𝛫𝛬, μήκους 𝑙 = 20 cm και μάζας 𝑚 = 200 g, είναι στερεωμένος στο κάτω άκρο ιδανικού κατακόρυφου ελατηρίου σταθεράς 𝑘 = 20 N/m, το επάνω άκρο του οποίου είναι       στερεωμένο σε οροφή,  έτσι ώστε ο αγωγός να είναι πάντα οριζόντιος. 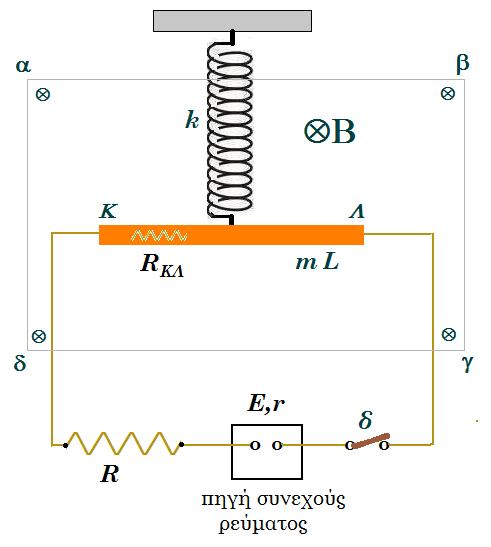Αρχικά ο διακόπτης είναι κλειστός. ο αγωγός ΚΛ  διαρρέεται από ηλεκτρικό ρεύμα σταθερής έντασης και φοράς.  Η όλη διάταξη  αβγδ   βρίσκεται μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης 𝐵⃗   μέτρου  B = 4 T, με αποτέλεσμα ο αγωγός 𝛫𝛬, να ισορροπεί ακίνητος και το ελατήριο να έχει το φυσικό του μήκος. 
4.1.  Να προσδιορίσετε την πολικότητα της πηγής του συνεχούς ηλεκτρικού ρεύματος.     Μονάδες 4 
Τη χρονική στιγμή 𝑡₀ = 0,  ανοίγουμε τον διακόπτη  με αποτέλεσμα ο αγωγός 𝛫𝛬 να πάψει να διαρρέεται από ηλεκτρικό ρεύμα  και  να αρχίσει να ταλαντώνεται.   Οι αντιστάσεις αέρα μπορούν να αγνοηθούν.    Θετική κατεύθυνση κατακόρυφη προς τα κάτω.
4.2.  Να αποδείξετε ότι η ταλάντωση που εκτελεί ο αγωγός 𝛫𝛬 είναι απλή αρμονική και να υπολογίσετε την κυκλική συχνότητά της.      Μονάδες 4
4.3.  Να εκφράσετε την δυναμική ενέργεια ελατηρίου  καθώς και την δύναμη του ελατηρίου που ασκείται στον αγωγό στην διάρκεια της ταλάντωσής του  όπως επίσης την δυναμική ενέργεια της ταλάντωσης του αγωγού.   Ποιές είναι οι ακραίες τιμές τους;   Μονάδες 12
4.4.  Να εκφράσετε την διαφορά δυναμικού 𝑉_𝛫 − 𝑉_𝛬 που επάγεται στα άκρα του αγωγού 𝛫𝛬,  συναρτήσει  του χρόνου από τη στιγμή που άρχισε η ταλάντωσή του.      Μονάδες 5

Θέμα Δ    28546

Δ.1.   ΣF  =  0  =>   mg  =  B i l  =>    0,2  10  =  4   i  0,2  =>   i = 2,5 A    από το Κ προς το Λ  

Δ.2.   ανοικτός ο διακόπτης :   ΣF  =  mg  +  F_ελατ  =   m α  =>    mg  +  k x  =   m x"     

θέση ισορροπίας :    ΣF  =  mg  +  F_ελατ  = 0  =>  mg  -  k x₀   = 0  =>  x₀  =  mg / k  =  2 / 20 = 0,1 m   επιμήκυνση  

τυχαία θέση :    ΣF  =  mg  +  F '_ελατ  =  mg  -  k (x₀ + χ)  =   k x₀  -  k (x₀ + χ)  = - k χ    η συνισταμένη δύναμη είναι ανάλογη της απομάκρυνσης       η σταθερά ταλάντωσης  D = k = m ω²  =>  20 = 0,2 ω²  =>  ω = 10 rad/s   

  x  =  A  ημ(ωt + φ)  =  0,1 ημ(10t + 3π/2)   ο αγωγός ΚΛ  ξεκινά την ταλάντωσή του από την άνω ακραία θέση ( - Α )  διότι  θετική κατεύθυνση κατακόρυφη προς τα κάτω 

            x (t) =  0,1 ημ(10t + 3π/2)           υ (t) = 1 συν(10t + 3π/2)              α (t) =  - 10 ημ(10t + 3π/2)    

Δ.3.    το ελατήριο έχει μέγιστη δυναμική ενέργεια όταν ο αγωγός ΚΛ  βρίσκεται στην κάτω ακραία θέση της ταλάντωσής του  οπότε το ελατήριο έχει επιμήκυνση  2Α = 0,2 m    U = ½ k (2A)²  =  ½  20  (0,2)²  =  0,4 Joule     

  U = ½ k x²  =>  U(t)  =  ½  20  [ 0,1 ημ(10t + 3π/2) ]²  =  0,1 ημ²(10t + 3π/2)   δυναμική ενέργεια ταλάντωσης του αγωγού ΚΛ  

  U (0)  =  0,1 ημ²(3π/2)  =  0,1 J       U(T/2)  =   0,1 ημ²(2π/Τ Τ/2  + 3π/2) =   0,1 ημ²(π  + 3π/2)  = 0,1 J  

  U(T/4)  =   0,1 ημ²(2π/Τ Τ/4  + 3π/2) =   0,1 ημ²(π/2  + 3π/2)  = 0 J   =  U(3T/4)

 U_ελατ  =  ½ k (x₀ + x)²  =>   U_ελατ (t)  =  ½  20  [ 0,1  +  0,1 ημ(10t + 3π/2) ]²  = 10  [ 0,1  +  0,1 ημ(10t + 3π/2) ]²     δυναμική ενέργεια ελατηρίου      

    U_ελατ (0)  = 10  [ 0,1  +  0,1 ημ(3π/2) ]²  = 10  [ 0,1  -  0,1 ]²   =  0  

   U_ελατ (T/2)  = 10  [ 0,1  +  0,1 ημ(2π/Τ Τ/2 + 3π/2) ]²  = 10  [ 0,1  +  0,1 ημ(π + 3π/2) ]²  = 10 [ 0,1 + 0,1 ]²  = 0,4 J   

  ΣF  = m a  =>  mg  +  F_ελατ  =  m a  =>  F_ελατ  =  m a  -  m g  = 0,2 [ - 10 ημ(10t + 3π/2) ]  -  2  =>

                   =>    F_ελατ (t)  =  - 2  -  2 ημ(10t + 3π/2)           F_ελατ (0) =  - 2  -  2 ημ(3π/2)  =  - 2  - 2 (-1) = 0  

   F_ελατ (Τ/2)  =  - 2  -  2 ημ(2π/Τ Τ/2  + 3π/2)   =  - 2  -  2 ημ(π  + 3π/2)    =  - 2  -  2 =  - 4 Ν     με φορά προς τα επάνω 

Δ.4.   V(t)  =  Ε_επαγ  =  B l v(t)  = 4   0,2   1 συν(10t + 3π/2)   =  0,8 συν(10t + 3π/2)  =  V_ΛΚ (t)  

    V_ΛΚ (0)  =  0,8 συν(3π/2)  =  0             V_ΛΚ (Τ/4)  =  0,8 συν(2π/Τ Τ/4  + 3π/2)  =  0,8 συν(π/2 + 3π/2)  =  0,8 Volt   ο αγωγός κινείται προς τα κάτω  μέσα στο μαγνητικό πεδίο   οπότε τα ηλεκτρόνια δέχονται δύναμη  Lorentz  με συνέπεια να μετακινούνται προς το άκρο  Κ  το οποίο φορτίζεται αρνητικά  ένω συγχρόνως  το άκρο  Λ  φορτίζεται θετικά

   V_ΛΚ (Τ/2)  =  0,8 συν(2π/Τ Τ/2  + 3π/2)  =  0,8 συν(π + 3π/2)  =  0,8  0  =  0 

  V_ΛΚ (3Τ/4)  =  0,8 συν(2π/Τ 3Τ/4  + 3π/2)  =  0,8 συν(3π/2 + 3π/2)  =  0,8 συν(π)  =  - 0,8 Volt   ο αγωγός κινείται προς τα επάνω  μέσα στο μαγνητικό πεδίο   οπότε τα ηλεκτρόνια δέχονται δύναμη  Lorentz  με συνέπεια να μετακινούνται προς το άκρο  Λ  το οποίο φορτίζεται αρνητικά  ένω συγχρόνως  το άκρο  Κ  φορτίζεται θετικά

       τελικά    V_ΚΛ (t)  = - 0,8 συν(10t + 3π/2)         θετική κατεύθυνση κατακόρυφη προς τα κάτω