Ε.Ε.Φ.  2023

ΘΕΜΑ 1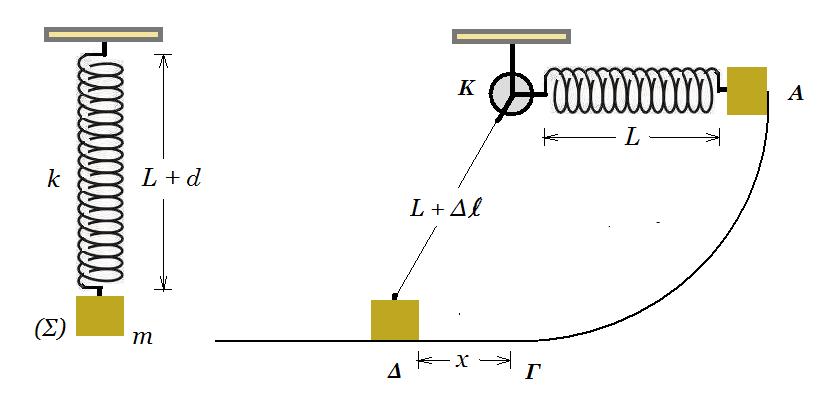Ιδανικό αβαρές ελατήριο σταθεράς k με φυσικό μήκος L είναι κατακόρυφο, με το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Στο κάτω άκρο του ελατηρίου κρέμεται μικρό σώμα (Σ) μάζας m, το οποίο ηρεμεί, ενώ το ελατήριο έχει επιμήκυνση ίση με d.  
Στη συνέχεια τοποθετούμε το σύστημα ελατήριο-σώμα σε λείο κατακόρυφο τεταρτοκύκλιο ΑΓ  ακτίνας R = L και κέντρου Κ, έτσι ώστε ο άξονάς του να είναι οριζόντιος και να συμπίπτει με την οριζόντια ακτίνα του τεταρτοκυκλίου.  Το μικρό σώμα (Σ) ακουμπάει στο πάνω άκρο Α του τεταρτοκυκλίου, ενώ παραμένει ενωμένο στο ένα άκρο του ελατηρίου. Το άλλο άκρο του ελατηρίου είναι συνδεδεμένο στο κέντρο Κ του τεταρτοκυκλίου με τέτοιο τρόπο, ώστε το σύστημα ελατήριο-σώμα να μπορεί να περιστρέφεται χωρίς τριβές. Αφήνουμε το σώμα (Σ) από το άκρο Α ελεύθερο να κινηθεί. Το σώμα (Σ) περνάει από το κάτω άκρο Γ του τεταρτοκυκλίου και συνεχίζει να κινείται πάνω σε λείο οριζόντιο επίπεδο, χωρίς να χάσει ποτέ την επαφή του με αυτό. Το σώμα (Σ) σταματάει στιγμιαία, αφού διανύσει απόσταση x στο οριζόντιο επίπεδο.  Η απόσταση x ισούται με : 

  α)   √( L (d + √(2 L d) ) )           β)   √( 2 L (d + √(2 L d) ) )    

  γ)   √( L (2d + √(2 L d) ) )         δ)   √( 2L (2d + √(2 L d) ) )       

  ισορροπία σώματος :   m g = k d  =>  k = mg/d  

  διατήρηση ενέργειας :   m g R  =  ½  m v_(Γ)²  =  ½  k  Δl²  =  ½  mg/d  Δl²  =>   v_(Γ)²  =  2gR         

    m g R  =  ½  mg/d  Δl²  =>   2 R d  = Δl²   =>   2 L d  = Δl² 

 πυθαγόρειο   (L + Δl)²  =  x² + L²  =>   L² + Δl² + 2 L Δl =  x²  +  L²  =>  L² + 2 L d  +  2 L √(2 L d)  =  x² + L² =>

    =>   2 L d  +  2 L √(2 L d)   =  x²  =>    √( 2 L d  +  2 L √(2 L d) )  =  x    (β)         

ΘΕΜΑ 3
Ένα σημειακό σώμα, μάζας m = 1 kg  είναι συνδεδεμένο στο άκρο ιδανικού ελατηρίου,  σταθεράς  k = 4π² N/m.  Το σύστημα, υπό την επίδραση διεγέρτη, εκτελεί εξαναγκασμένη ταλάντωση.  Ο διεγέρτης έχει συχνότητα  f = 2 Hz.   Ο λόγος της μέγιστης κινητικής ενέργειας Κ_max του σώματος προς τη μέγιστη δυναμική ενέργεια U_max της ταλάντωσης είναι:
α. 1     β. 2     γ. 4      δ. 1/4

 k = m ω₀²  =>  4 π²  = 1  4 π² f₀ ²  =>  f₀ = 1 Hz  <  2 Hz =  f_{διεγέρτη}   

 το σώμα ταλαντώνεται με την συχνότητα  f = 2 Hz του διεγέρτη            

   x  =  A ημωt  = A ημ(2πft)  =>   x  =  A ημ(4πt)                v  =  4π A συν(4πt)  

  U_max = ½ D A²  =  ½  k A²  =  ½  4π²  Α² 

  Κ_max  = ½ m  υ²  =   ½ m (4π)² A²                                      Κ_max / U_max = 4    (γ)

ΘΕΜΑ 4

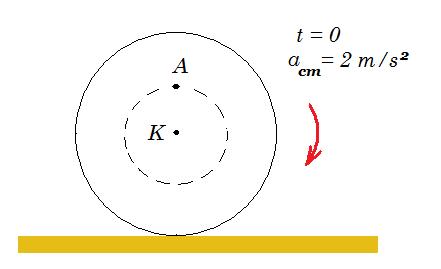
Ο ομογενής τροχός του σχήματος έχει ακτίνα  R = 2 m και κυλάει χωρίς να ολισθαίνει.  Έστω ένα σημείο Α του τροχού, το οποίο βρίσκεται σε απόσταση  r = 1 m πάνω από το κέντρο μάζας Κ  του τροχού και στην ίδια κατακόρυφη ευθεία με αυτό.  Ο τροχός ξεκινά τη χρονική στιγμή  t = 0,  χωρίς αρχική ταχύτητα, να επιταχύνεται με επιτάχυνση μέτρου  αcm = 2 m/s2. Το μέτρο της επιτάχυνσης του σημείου Α τη χρονική στιγμή t = 1 s  είναι : ..... και έχει διανύσει διάστημα :  ..........

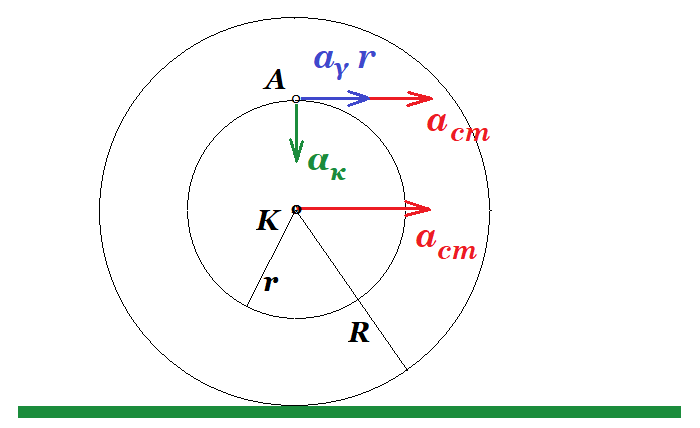
 α_γων  =  α_cm / R  =  2 m/s² / 2 m  =  1 rad/s²            ω  =  α_γων t  = 1 rad/s² 1 s  = 1 rad/s              

κεντρομόλος επιτάχυνση στο σημείο Α :    α_κ =  υ² / r  =  ω² r  =  1²  1 = 1 m/s²      

a_A² = ( a_cm + α_γων r )² + α_κ²  =>  a_A² = ( 2 m/s²  + 1 rad/s² 1 m )² + ( 1 m/s² )² => α_Α² = 10  =>  α_Α = √10 m/s²

 x_cm  =  ½  α_cm  t²  =  ½  2 m/s²  1 s²  =  1 m         

θ  =  ½  α_γων t²  =  ½  1 rad/s²  1 s²  =  0,5 rad                          l_A = θ r =  0,5 rad  1 m =  0,5 m      

   x_A = x_cm + l_A  =  1 m +  0,5 m  =>   x_A =  1,5 m   

ΘΕΜΑ 5
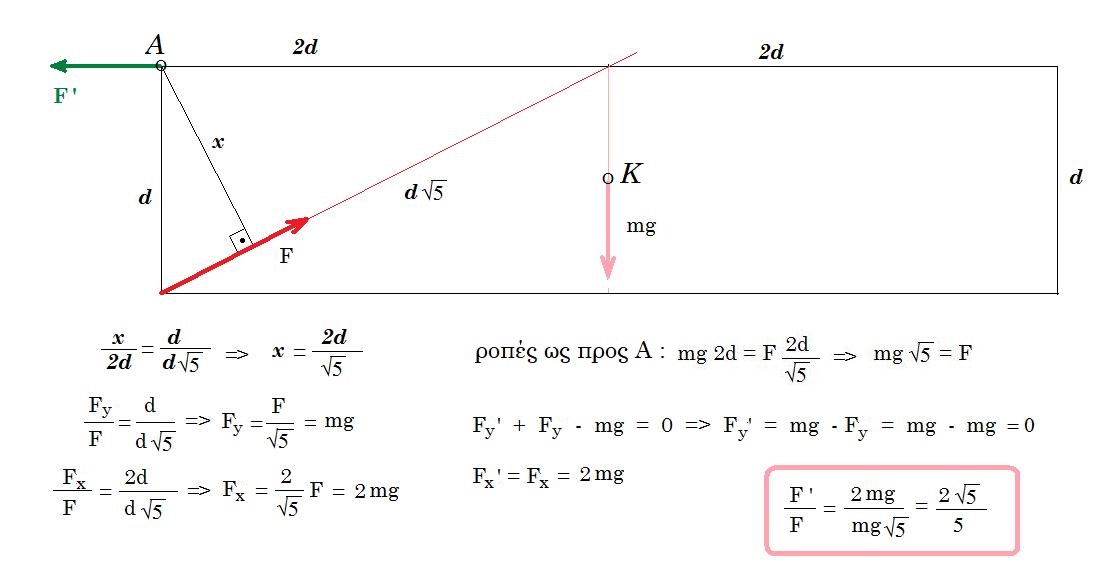
Μια ομογενής κατακόρυφη και ορθογώνια πόρτα έχει πλάτος τετραπλάσιο από το ύψος της d και στηρίζεται με μεντεσέδες στα δύο άκρα της σε κατακόρυφο τοίχο.  Η διεύθυνση της δύναμης από τον κάτω μεντεσέ διέρχεται από το μέσο της ανώτερης πλευράς της.  Ο λόγος των μέτρων των δυνάμεων που ασκούνται από τον επάνω προς τον κάτω μεντεσέ αντίστοιχα είναι:

  α)   √5                   β)   2 ^. √5                γ)    √5 / 5                δ)    2 ^. √5 / 5     

ΘΕΜΑ 6
Ένα ομογενές δοκάρι με μήκος L  και βάρος w ισορροπεί οριακά ανάμεσα σε δύο κατακόρυφους
τοίχους από τους οποίους ο ένας είναι λείος και με τον άλλον εμφανίζεται τριβή στο σημείο
επαφής τους με συντελεστή μ.  Η απόσταση μεταξύ των τοίχων είναι ίση με: 

  α)   L / √(μ² + 4)           β)   2L / √(μ² + 4)             γ)    L / √(μ² - 4)              δ)   2L / √(μ² - 4)  

Τ ' = Τx        Ty = mg             Ty  =  μ Tx   =>    Tx  =  Ty / μ  =  mg / μ                   ροπές :  mg x/2  =  T ' y    =>     =>   y  =   mg x / 2T ' =   mg x / 2Tx =   mg x / (2mg/μ)  =>   y  =  x μ/2             x2  +  y2  =  L2  =>   x2  +  ( x μ/2 )2  =  L2  =>   x2  ( 1 + μ2/4 )  =  L2  =>  =>    x2  ( 4 + μ2 ) / 4  =  L2  =>   x2  =  4 L2 / ( 4 + μ2 )  =>                     x  =  2L / ( 4 + μ2 )½

ΘΕΜΑ 7
Η ένταση του μαγνητικού πεδίου στο κέντρο κυκλικού ρευματοφόρου αγωγού ακτίνας r  που
διαρρέεται από ρεύμα έντασης Ι₁ = 10 mA είναι Β₁.  Ηλεκτρικό φορτίο q=50μC κινείται με
συχνότητα  f  σε κυκλική τροχιά ακτίνας r,  στο κέντρο της οποίας η ένταση του μαγνητικού πεδίου
είναι Β₂ = 2Β₁.  Η συχνότητα περιστροφής του ηλεκτρικού φορτίου είναι:
α. 100 Hz      β. 200 Hz       γ. 400 Hz         δ. 1000 Hz

   Β₁  =  10^-7 2π Ι₁ / r            Β₂  =  10^-7 2π Ι₂ / r           I₂  =  q/T  =  q f           f = 1/T  

     B₂  =  2Β₁  =>  10^-7 2π q f / r   =  2  10^-7 2π Ι₁ / r  =>  q f  =  2 Ι₁  =>  50 ^.10^-6  f  =  2 ^.10^-2  =>    

  =>    f  =  2/50  10⁴  Hz   =  400 Hz     (γ)     

ΘΕΜΑ Β.        Αριστοτέλης 2023

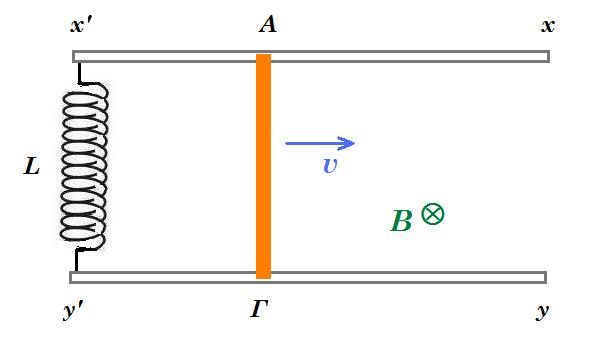
Ο αγωγός ΑΓ, μήκους l = 0,4 m, μάζας m = 0,2 kg και αμελητέας αντίστασης  κινείται οριζόντια σε επαφή με δύο ευθύγραμμους αγωγούς x΄x και y΄y, οι οποίοι δεν παρουσιάζουν αντίσταση και απέχουν κατά l = 0,4 m, ενώ στα άκρα τους x΄και y΄ συνδέεται ένα ιδανικό πηνίο  το οποίο φέρει 1000 σπείρες ανα μέτρο, με συντελεστή αυτεπαγωγής L = 0,2 Η. Το όλον σύστημα βρίσκεται μέσα σε ένα κατακόρυφο ομογενές μαγνητικό πεδίο έντασης Β = 0,5 Τ, όπως στο σχήμα. Μια χρονική στιγμή t₀ = 0, εκτοξεύουμε τον αγωγό ΑΓ με ταχύτητα υ₀ = 2 m/s, με φορά προς τα δεξιά.

Β.1.   Βρείτε την χρονική στιγμή  t₁  όπου η ταχύτητα του αγωγού μηδενίζεται.

Β.2.   Βρείτε την μετατόπιση σε σχέση με την θέση εκτόξευσης  Δx  του αγωγού την ίδια στιγμή.

Β.3.   Πόση είναι η ενέργεια  U_B  στο μαγνητικό πεδίο του πηνίου τότε;

θα μελετήσουμε την κίνηση του αγωγού ΑΓ 

επειδή κινείται κάθετα στις δυναμικές γραμμές του μαγνητικού πεδίου τα ηλεκτρόνιά του δέχονται δύναμη Lorentz  με συνέπεια να μετακινούνται προς το άκρο Γ  το οποίο φορτίζεται αρνητικά  ενώ το άκρο Α  φορτίζεται θετικά  εμφανίζεται επαγωγική τάση  Ε_επαγ  =  Β υ l   τότε δημιουργείται κύκλωμα με τους αγωγούς και το ιδανικό πηνίο και διαρρέεται από επαγωγικό ρεύμα   ενώ στα άκρα του πηνίου εμφανίζεται τάση αυτεπαγωγής  Ε_ΑΥΤ  =  - L di/dt  με πολικότητα  x' (+)  y' (-)  

ισχύει η σχέση :  Ε_επαγ  +  Ε_ΑΥΤ  =  0 =>  Β υ l  -  L di/dt  =  0  (1)  

ο αγωγός ΑΓ  διαρρέεται από ρεύμα  μέσα σε μαγνητικό πεδίο  άρα  δέχεται  δύναμη  Laplace  αντίρροπη της ταχύτητάς του    ΣF = m a  =>  - F_L  =  ma  =>  - B i l  =  m dv/dt  =>  i  =  - m/Bl dv/dt    (2)                 di/dt  =  - m/Bl d²v/dt²   (3)

  (1) , (3) =>   Β υ l  - L di/dt   =  0  =>   B v l  -  L  [ - m/Bl d²v/dt² ]  =  0  => 

                =>  B v l  +  mL/Bl  d²v/dt²  =  0   =>   d²v/dt²  +  B²l²/mL v  =  0    (4)  

 v(t)  =  v₀  συνωt            α = dv/dt  =>  α(t)  =  - ωv₀  ημωt             x(t)  =  v₀/ω  ημωt = Α ημωt   

 ο αγωγός εκτελεί Α.Α.Τ.  με γωνιακή συχνότητα  ω²  =  B²l²/mL =  ( 0,5² 0,4² ) / ( 0,2 0,2 )  => 

          =>   ω = 1 rad/s    η περίοδος της ταλάντωσης :  Τ  =  2π / ω  =  2π sec

B.1.  ο αγωγός θα σταματήσει για 1η φορά τη χρονική στιγμή  t₁ = T/4 =  π/2 sec     

η αρχική ταχύτητα υ₀  είναι η μέγιστη ταχύτητα του αγωγού κατά την ταλάντωσή του τη στιγμή που διέρχεται από τη θέση ισορροπίας του 

B.2. η μετατόπισή του θα είναι ίση με το πλάτος της ταλάντωσης  Α = υ₀ / ω = 2 m/s / 1 rad/s = 2m

η δυναμική ενέργεια του μαγνητικού πεδίου του πηνίου τη χρονική στιγμή  t₁  ισούται με την αρχική κινητική ενέργεια του αγωγού  διότι δεν υπάρχει απώλεια ενέργειας  ούτε δυνάμεις τριβής  ούτε αντίσταση αέρα  ούτε φαινόμενο Joule  διότι οι αντιστάσεις στους αγωγούς είναι αμελητέες

B.3.        U_B  =  K₀  =  0,5  m  v₀²  =  0,5  0,2  2²  =  0,4 Joule

 v(t)  =  v₀  συνωt = 2 συνt          

α = dv/dt  =>  α(t)  =  - ωv₀  ημωt  =  - 2 ημt        

 x(t)  =  v₀/ω  ημωt = Α ημωt  =  2 ημt 

(2) =>   i  =  - m/Bl dv/dt  =  - m/Bl  ( - ωv₀  ημωt )  =  + mωv₀ / Bl  ημωt  =  0,2 1 2 / 0,5 0,4 ημt  =>  i(t) = 2 ημt  

  F_L  =  B l i  =  0,5  0,4  2 ημt  =  0,4 ημt    το μέτρο της δύναμης Laplace  που ασκείται στον αγωγό ΑΓ  μεταβάλλεται  ημιτονοειδώς με τον χρόνο

ενέργεια μαγνητικού πεδίου στο πηνίο :  U_B  =  0,5 L i²  =  0,5  0,2  4 ημ²t   =  0,4 ημ²t  

ένταση μαγνητικού πεδίου στο πηνίο :  B  =  4π 10^-7 n  i(t)  =  4π 10^-7  1000  2 ημt  =  8π 10^-4 ημt