α υ τ ε π α γ ω γ ή - π η ν ί ο υ

E - L di/dt = i R => di/dt = (E - i R) / L = - R/L (i - E/R) => di / (i - E/R) = - R/L dt =>

ln [ (i - E/R) / (- E/R) ] = - R/L (t - t₀) => i(t) = E/R ( 1 - e^{- R/L (t - t₀)} )

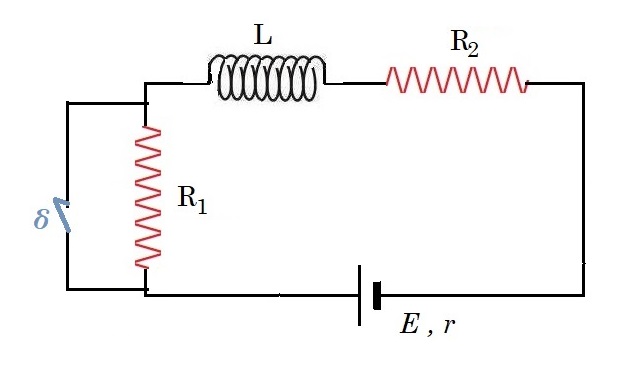
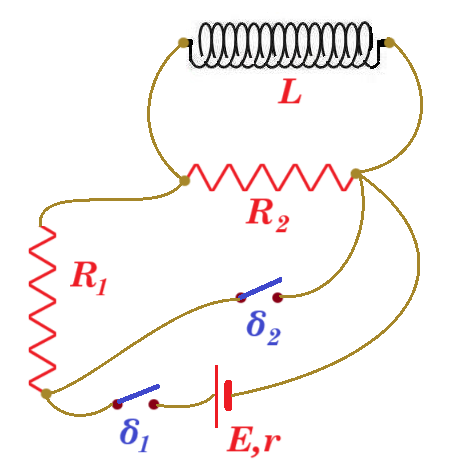Για το κύκλωμα του σχήματος, η πηγή έχει ΗΕΔ Ε=12V και εσωτερική αντίσταση r=2Ω, οι δυο αντιστάτες έχουν αντίσταση R₁=R₂=2Ω και το ιδανικό πηνίο συντελεστή αυτεπαγωγής L=0,4Η, ενώ οι δυο διακόπτες είναι ανοιχτοί.

i) Σε μια στιγμή t₀=0 κλείνουμε τον διακόπτη δ₁. Για την στιγμή αμέσως μετά (για t=t₀⁺) να βρεθούν η ισχύς της πηγής, η ΗΕΔ από αυτεπαγωγή στο πηνίο, καθώς και ο ρυθμός μεταβολής της έντασης του ρεύματος di/dt, που το διαρρέει.

ii) Σε μια στιγμή t₁ ο αντιστάτης R₁διαρρέεται από ρεύμα έντασης i₁=2,5Α. Για τη στιγμή αυτή να βρεθεί η ενέργεια του μαγνητικού πεδίου του πηνίου καθώς και ο ρυθμός μεταβολής της ενέργειας αυτής.

iii) Μόλις σταθεροποιηθεί η ένταση του ρεύματος που διαρρέει την πηγή, σε μια στιγμή t₂, κλείνουμε τον διακόπτη δ₂, ανοίγοντας ταυτόχρονα το διακόπτη δ₁. Να βρεθεί η ένταση του ρεύματος που διαρρέει την αντίσταση R₂, αμέσως τη στιγμή t₂, καθώς και ο ρυθμός μεταβολής της έντασης του ρεύματος που διαρρέει το πηνίο.

όταν κλείνουμε τον δ₁ το πηνίο αντιδρά και αρχικά δεν διαρρέεται από ρεύμα έτσι η πηγή η R₁ και η R₂ συνδέονται σε σειρά E = i (r + R₁ + R₂) => 12 = i (2 + 2 + 2) => i = 2 A η ισχύς της πηγής είναι P_πηγής = E i = 12V 2A = 24 W το πηνίο συνδέεται παράλληλα στην R₂ άρα έχουν την ίδια τάση i R₂ = 2A 2Ω = 4V 4V = L di/dt => di/dt = 4V / 0,4H = 10 A/s

E = i (r + R₁) + i₂ R₂ => 12 = 2,5 (2 + 2) + i₂ 2 => 12 = 10 + i₂ 2 => i₂ = 1 A τότε i_L = 2,5 A - 1 A = 1,5 A U_L = 0,5 L i_L² = 0,5 0,4 1,5² = 0,45 J

μόλις σταθεροποιηθούν τα ρεύματα το ιδανικό πηνίο είναι απλό σύρμα χωρίς ωμική αντίσταση άρα το ρεύμα περνά μέσα από αυτό και όχι από την R₂ έτσι Ε = i (r + R₁) => 12 = i (2 + 2) => i = 3 A

όταν ανοίξουμε τον δ₁ και κλείσουμε τον δ₂ το πηνίο αρχικά διαρρέεται από ρεύμα 3Α οι αντιστάσεις R₁ , R₂ συνδέονται παράλληλα δίνοντας ισοδύναμη αντίσταση R_1,2 = 2 2 / (2+2) = 1 Ω από την R₂ θα περάσει ρεύμα 3Α / 2 = 1,5 Α ακόμη έχουμε - L di/dt = i R_1,2 => - 0,4 di/dt = 3 1 => di/dt = - 3 / 0,4 = - 30/4 = - 7,5 A/s

Το κύκλωμα του σχήματος περιλαμβάνει δυο λείους οριζόντιους αγωγούς x′x και y′y, χωρίς ωμική αντίσταση απέχουν απόσταση ℓ = 0,5 m. Στο αριστερό τους άκρο συνδέονται στα σημεία Α και Γ με ιδανικό πηνίο συντελεστή αυτεπαγωγής L = 2,5 mH. Τρίτος αρχικά ακίνητος αγωγός ΚΝ μάζας m = 0,04 kg, χωρίς ωμική αντίσταση και μήκους ℓ = 0,5 m μπορεί να κινείται μένοντας διαρκώς οριζόντιος με τα άκρα του σε συνεχή επαφή με τους αγωγούς x′x και y′y. Το επίπεδο του κυκλώματος είναι εντός ενός κατακόρυφου ομογενούς μαγνητικού πεδίου έντασης μέτρου Β = 0,2 Τ και του ομόρροπου γήινου ομογενούς βαρυτικού πεδίου έντασης μέτρου g = 10 m/s². Τη χρονική στιγμή t₀ = 0, δίνουμε στον αγωγό ΚΝ οριζόντια ταχύτητα υ₀ = 2 m/s παράλληλη στους αγωγούς x′x και y′y. Να αποδειχθεί ότι:

Δ1. Ο αγωγός ΚΝ θα εκτελέσει αρμονική ταλάντωση και να παρασταθεί γραφικά η συνισταμένη δύναμη ΣF που δέχεται σε συνάρτηση με την απομάκρυνση x.

Δ2. Το ρεύμα που διαρρέει τον αγωγό ΚΝ είναι εναλλασσόμενο και να παρασταθεί γραφικά η ένταση του i σε συνάρτηση με το χρόνο κίνησης του t.

Δ3. Το άθροισμα της κινητικής ενέργειας Κ του αγωγού ΚΝ και της ενέργειας U_B του μαγνητικού πεδίου του πηνίου είναι σταθερό και να γίνει το διάγραμμα Κ = f(U_B).

Δ4. Όταν ο ρυθμός μεταβολής της ταχύτητας του αγωγού ΚΝ έχει μέτρο ίσο με το μισό του μέγιστου που αποκτά κατά τη διάρκεια της ταλάντωσης να βρεθεί ο ρυθμός διέλευσης ηλεκτρονίων από μια διατομή του.

Δίνεται το στοιχειώδες ηλεκτρικό φορτίο e = 1,6∙10^–19 C.

Ε_επαγ + Ε_ΑΥΤ = i R = 0 => B v l - L di/dt = 0 => B l dx/dt = L di/dt => B l Δx/Δt = L Δi/Δt =>

=> B l (x - 0) = L (i - 0) => Β l x = L i => i = Bl/L x = 0,2T 0,5m / 0,0025H x => i = 40.x

ΣF = m a => m a = - B l i => 0,04 a = - 0,2 0,5 40.x => a = - 100 x ω² = 100 => ω = 10 rad/s T = 2π/10 = π/5 s

K_max = U_L,max => 0,5 m v₀² = 0,5 L I² => I = (m/L) v₀ = (0,04/0,0025) 2 = 4 2 => Ι = 8 A μέγιστη ένταση ρεύματος που διαρρέει την ράβδο και το πηνίο Ι = 40 x_max => 8 = 40 x_max => x_max = 0,2 m μέγιστη απομάκρυνση της ράβδου από τη θέση ισορροπίας της ( πλάτος ταλάντωσης της ράβδου )

η ράβδος εκτελεί Α.Α.Τ. με πλάτος 0,2 m και περίοδο π/5 s x = 0,2 ημ(10π.t) αρχικά βρίσκεται στη θέση ισορροπίας της τότε το ρεύμα i = 40.x = 40 0,2 ημ(10π.t) => i(t) = 8 ημ(10π.t)

K_max = U_L,max = K + U_L => K + U_L = 0,5 m v₀² = 0,5 0,04 2² => K + U_L = 0,08 J => K = 0,08J - U_L

i = 40 x = 40 0,1 => i = 4 A = dq/dt = e dN/dt => dN/dt = 4 A / 1,6 10^-19 C = 2,5 10¹⁹ ηλκτρόνια/s

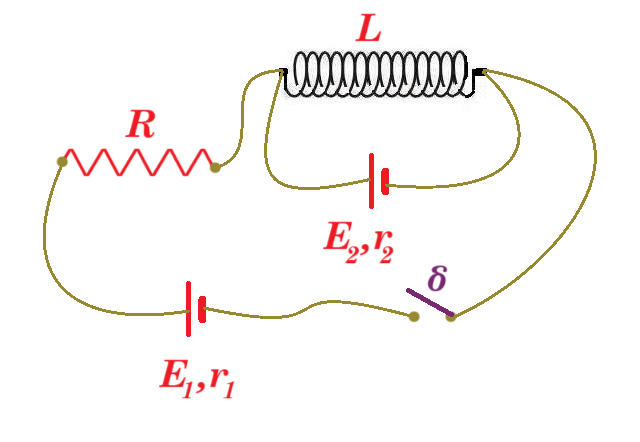Δίνεται το παραπάνω κύκλωμα με το διακόπτη δ κλειστό και σταθερές εντάσεις ρευμάτων. Το πηνίο είναι ιδανικό με συντελεστή αυτεπαγωγής L=0,2Η, Ε₁=20V, r₁=1Ω, Ε₂=2V, r₂=1Ω και R=3Ω.

i) Να υπολογιστεί η ενέργεια του μαγνητικού πεδίου του πηνίου και η ισχύς κάθε πηγής.

ii) Σε μια στιγμή t₁ανοίγουμε το διακόπτη. Για την στιγμή αμέσως μετά το άνοιγμα του διακόπτη, να βρεθούν:

α) Η ένταση του ρεύματος που διαρρέει κάθε πηγή.

γ) Η ισχύς της πηγής Ε₂ και η ισχύς του πηνίου.

iii) Ποια είναι τελικά η ενέργεια που αποθηκεύεται στο πηνίο;

ο διακόπτης είναι κλειστός οι εντάσεις των ρευμάτων είναι σταθερές, τα άκρα της πηγής 2 βραχυκυκλώνονται η πηγή 2 "βγάζει" ρεύμα έντασης i₂ = E₂ / r₂ = 2V / 1Ω = 2Α, η πηγή 1 "βγάζει" ρεύμα έντασης i₁ , το ιδανικό πηνίο διαρρέεται από ρεύμα i_π = i₁ + i₂ έχουμε κύκλωμα σε σειρά την πηγή 1, τον διακόπτη, την αντίσταση, το πηνίο : E₁ = i (r₁ + R) => 20V = i (1Ω + 3Ω) => i = 5A

τότε i_π = i₁ + i₂ = 5Α + 2Α = 7Α U_L = 0,5 i² L = 0,5 7² 0,2 = 4,9 J

όταν ανοίξουμε τον διακόπτη δ η πηγή 1 δεν διαρρέεται από ρεύμα , το πηνίο αντιδρά και αρχικά διαρρέεται από ρεύμα 7Α της ίδιας φοράς (δεξιά) τότε η πηγή 2 διαρρέεται από ρεύμα 7 Α το πηνίο και η πηγή 2 είναι σε σειρά σύνδεση ίδιας πολικότητας

E₂ + L di/dt = i r₂ => 2 + 0,2 di/dt = 7 1 => di/dt = (2 - 7) / 0,2 = -5/0,2 = -25 A/s

P_E2 = E₂ i = 2V 7A = 14 W P_L = L i |di/dt| = 0,2 7 25 = 35 W P_r = i² r = 7² 1 = 49 W

αργότερα μετά από χρόνο το ιδανικό πηνίο διαρρέεται από ρεύμα : i' = E₂ / r₂ = 2V / 1Ω = 2Α

U_L' = 0,5 L i'² = 0,5 0,2 2² = 0,4 J τελική δυναμική ενέργεια που αποθηκεύεται στο πηνίο

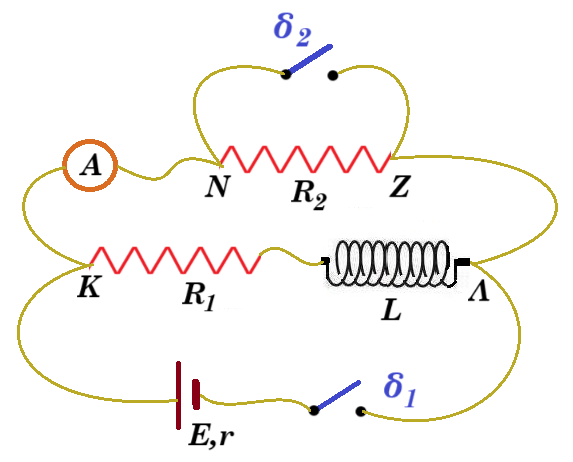
Το κύκλωμα του σχήματος 1 περιλαμβάνει πηγή με τιμή ΗΕΔ Ε=12V εσωτερική αντίσταση r=1Ω ιδανικό πηνίο με συντελεστή αυτεπαγωγής L=1mΗ, ωμικό αντιστάτη ωμικής αντίστασης R₁=6Ω, αντιστάτη R₂=3Ω και ιδανικό αμπερόμετρο που είναι τοποθετημένο στον κλάδο ΚΜ. Αρχικά οι διακόπτες δ₁ και δ₂ είναι ανοιχτοί. Κάποια στιγμή που θεωρούμε t=0 κλείνουμε το διακόπτη δ₁. Να βρείτε:

α) την ένδειξη του αμπερομέτρου τη στιγμή που κλείνουμε τον διακόπτη.

β) τις τελικές τιμές των ρευμάτων ύστερα από την αποκατάσταση του κυκλώματος και την ενέργεια που θα αποθηκεύσει το πηνίο.

Μια επόμενη χρονική στιγμή t₁ βραχυκυκλώνουμε τον αντιστάτη R₂ κλείνοντας το διακόπτη δ₂.

γ) περιγράψτε την εξέλιξη του φαινομένου.

Για τη στιγμή αμέσως μετά το κλείσιμο του διακόπτη δ₂ να βρείτε:

δ) το ρεύμα που διαρρέει

i) τον αντιστάτη R_2.

ii) τον αντιστάτη R₁.

iii) την πηγή.

iv) την ένδειξη του αμπερομέτρου.

ε) το ρυθμό μεταβολής της μαγνητικής ενέργειας του πηνίου.

α) το πηνίο αντιδρά και δεν αφήνει το ρεύμα να περάσει από την αντίσταση R₁

το ρεύμα της πηγής περνά από την αντίσταση R₂

νόμος του Ohm για κλειστό κύκλωμα : E = i (r + R₂) => 12 V = i (1Ω + 3Ω) => i = 3A η ένδειξη του αμπερομέτρου

β) μετά από ικανό χρόνο το πηνίο είναι απλό σύρμα με ωμική αντίσταση

νόμος του Ohm για κλειστό κύκλωμα : E = i (r + R_1,₂) => 12 V = i (1Ω + 2Ω) => i = 4A

i₁ = V_ΚΛ / R₁ = 8V / 6Ω = 4/3 A ρεύμα που διαρρέι το πηνίο από το Κ προς το Λ (δεξιά)

i₂ = V_ΚΛ / R₂ = 8V / 3Ω = 8/3 A η ένδειξη του αμπερομέτρου

η δυναμική ενέργεια του πηνίου : U_L = 0,5 L i₁² = 0,5 10^-3 ( 4/3 )² = 8/9 mJ

γ) μετά από ικανό χρόνο κλείνουμε τον διακόπτη δ₂ τότε το ρεύμα δεν θα περάσει από αντίσταση R₂ αλλά από τον διακόπτη δ₂ και έτσι βραχυκυκλώνεται και ο κλάδος της αντίστασης R₁ με το πηνίο το αμπερόμετρο είναι ιδανικό χωρίς ωμική αντίσταση το πηνίο αντιδρά και συνεχίζει να διαρρέεται από ρεύμα της ίδιας φοράς (δεξιά) i₁ = 4/3 Α

νόμος του Ohm για κλειστό κύκλωμα (βραχυκυκλώνεται η πηγή) : E = i r => 12V = i 1Ω => i = 12A τελική τιμή

το αμπερόμετρο διαρρέεται από ρεύμα : i₂ = i - i₁ = 12A - 4/3A = 32/3A

- L di₁ / dt = i₁ R₁ = 4/3 6 = 8 V => - 10^-3 di₁ / dt = 4/3 6 => di₁ / dt = - 8000 A/s

Η πηγή δεν έχει εσωτερική αντίσταση. Το πηνίο έχει 100 σπείρες και αμελητέα αντίσταση.
Τη στιγμή μηδέν κλείνουμε τον διακόπτη. Διαθέτουμε τις παρακάτω τρεις καμπύλες για το ρεύμα, την τάση V_ΑΓ και την μαγνητική ροή που περνάει από κάθε σπείρα του πηνίου.

1. Βρείτε την Ε και την R.
2. Βρείτε τον συντελεστή αυτεπαγωγής του πηνίου.
3. Με ποιο ρυθμό μεταβάλλεται το ρεύμα όταν έχει την τιμή 2 Α ;
4. Βρείτε τη μέγιστη τιμή της ισχύος που τροφοδοτεί το πηνίο.

E - L di/dt = i R τη στιγμή μηδέν i = 0 E = L di/dt = V_ΑΓ = 100 Volt πολύ αργότερα i = 10 A V_ΑΓ = 0 E = iR => 100 V = 10 A R => R = 10 Ohm

E_ΑΥΤ = - L Δi/Δt = - N ΔΦ/Δt => L ΔI = Ν ΔΦ => L (I - 0) = Ν (Φ - 0) => L I = Ν Φ => L = N Φ / I = 100 10^-4 Wb / 10 A => L = 10^-3 Henry = 1 mH

E i = i² R + P_πην => 10 i² - 100 i + P_πην = 0 Δ = 10000 - 4 10 P_πην ³ 0 => P_πην £ 250 ΅Watt

E - L di/dt = i R => - L di/dt = i R - E => - L di/dt = R (i - E/R) => di / (i - E/R) = - R/L dt =>

=> ln [(i - E/R) / (- E/R) = - R/L t => i - E/R = - E/R e^-R/L.t => i(t) = E/R (1 - e^-R/L.t) τ = L/R i(5τ) = E/R

t₁ : i₁ > i₂ => 1 - e^-R/L1.t1 > 1 - e^-R/L2.t1 => - e^-R/L1.t1 > - e^-R/L2.t1 => e^-R/L1.t1 < e^-R/L2.t1 =>

=> 1/ e^R/L1.t1 < 1 / e^R/L2.t1 => e^R/L1.t1 > e^R/L2.t1 => R/L₁ t₁ > R/L₂ t₁ => L₂ > L₁

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~`

E - L di/dt = i R₁ => 20 - 0,4 di/dt = 2 4 => di/dt = 12 / 0,4 = 30 A/s - L di/dt = - 0,4 30 = - 12 Volt U = 0,5 L i² = 0,5 0,4 2² = 0,8 J dU/dt = L i di/dt = 0,4 2 30 = 24 J/s

E = i₁ R₁ + V_ΒΓ => 20 = 3 4 + V_ΒΓ => V_ΒΓ = 8 V i₂ = V_ΒΓ / R₂ = 8 V / 4 Ω => i₂ = 2 Α άρα i₃ = 1 Α V_ΒΓ = - L di/dt => 8 V = - 0,4 H di/dt => di/dt = - 20 A/s

dU/dt = L i di/dt = 0,4 1 ( - 20 ) = - 8 J/s τελικά το ιδανικό πηνίο διαρρέεται από ρεύμα i = E / R₁ = 20 / 4 = 5 A U= 0,5 L i² = 0,5 0,4 5² = 5 J

Για το κύκλωμα του διπλανού σχήματος, δίνονται Ε=20V (r=0), R₁=R₂=4Ω, ενώ το πηνίο είναι ιδανικό με συντελεστή αυτεπαγωγής L=0,4Η. Οι δύο διακόπτες είναι αρχικά ανοικτοί. Σε μια στιγμή t_ο=0, κλείνουμε τον διακόπτη δ₁, οπότε σε μια στιγμή t₁ το αμπερόμετρο δείχνει ένδειξη i=2Α.

i) Για τη στιγμή t₁ να υπολογιστεί η ΗΕΔ από αυτεπαγωγή πάνω στο πηνίο, η ενέργεια του μαγνητικού του πεδίου, καθώς και ο ρυθμός μεταβολής της ενέργειας αυτής.

ii) Αμέσως μετά την παραπάνω στιγμή, κλείνουμε και τον διακόπτη δ₂, οπότε σε μια επόμενη χρονική στιγμή t₂, το αμπερόμετρο δείχνει ένδειξη i₁=3Α. Για τη στιγμή αυτή ζητούνται:

α) Η ένταση του ρεύματος i₂ που διαρρέει την αντίσταση R₂, καθώς και η ένταση i₃ η οποία διαρρέει το πηνίο.

β) Η ΗΕΔ από αυτεπαγωγή που αναπτύσσεται στο πηνίο. Η ένταση του ρεύματος που διαρρέει τη στιγμή αυτή το πηνίο αυξάνεται ή μειώνεται;

iii) Πόση τελικά ενέργεια αποθηκεύεται στο πηνίο, μετά την λήξη των μεταβατικών φαινομένων;

Στο κύκλωμα του σχήματος το πηνίο είναι ιδανικό, με συντελεστή αυτεπαγωγής L=0,2H, η πηγή έχει Ε=12V, r=2Ω και ο αντιστάτης R=8Ω. Τη χρονική στιγμή t=0 περνάμε τον μεταγωγό στη θέση A. Να υπολογίσετε:
α. την τελική τιμή Ι₀του ρευματος.
β. τη μέγιστη ενέργεια μαγνητικου πεδίου που αποθηκευτηκε στο πηνίο.
γ. τον μέγιστο ρυθμό μεταβολής της έντασης του ρεύματος.
δ. την μέγιστη και την ελάχιστη τιμή της πολικής τάσης καθώς και την μέγιστη και την ελάχιστη τιμή της διαφοράς δυναμικού στα άκρα της αντίστασης R.
Τη στιγμή που ο αντιστάτης διαρρέεται από ρεύμα ένταςης i=0,2Α να υπολογίσετε:
ε. την E_AYTπου αναπτύσσεται στο πηνίο.
στ. τον ρυθμό μεταβολής της έντασης του ρεύματος.
ζ. την πολική τάση της πηγής.
η. την ισχύ σε κάθε στοιχείο του κυκλώματος: P_πηγής, P_r, P_R, P_πηνίου.

Για το κύκλωμα του σχήματος το πηνίο είναι ιδανικό, με συντελεστή αυτεπαγωγής L=0,1H, η πηγή έχει Ε=12V, r=1Ω και ο αντιστάτης R=9Ω. Τη χρονική στιγμή t=0 περνάμε τον μεταγωγό από τη θέση A στη θέση B. Να υπολογίσετε:
1. την αρχική τιμή Ι₀του ρεύματος.
2. τη μέγιστη ενέργεια μαγνητικου πεδίου που αποθηκεύτηκε στο πηνίο.
3. την αρχική τιμή της τάσης από αυτεπαγωγή στο πηνίο.
4. τον ελάχιστο ρυθμό μεταβολής της έντασης του ρεύματος.
Τη στιγμή που ο αντιστάτης διαρρέεται από ρεύμα έντασης i=0,5Α να υπολογίςετε:
5. την E_AYTπου αναπτύσσεται στο πηνίο.
6. τον ρυθμό μεταβολής της έντασης του ρεύματος.
7. την ισχύ σε κάθε στοιχείο του κυκλώματος: P_R, P_L.

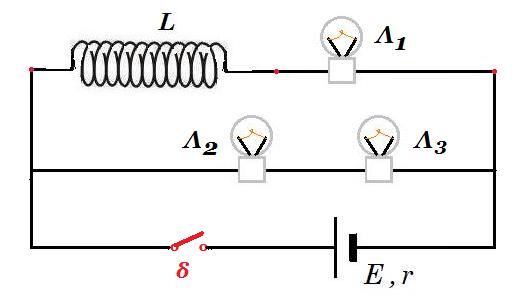
Στο κύκλωμα οι λαμπτήρες Λ₁, Λ₂, Λ₃ είναι όμοιοι. Η πηγή έχει ΗΕΔ Ε και εσωτερική αντίσταση r = 0. το πηνίο είναι ιδανικό τα καλώδια σύνδεσης δεν παρουσιάζουν αντίσταση. Την t₀ = 0 κλείνουμε το διακόπτη. Τη στιγμή που ο ρυθμός αύξησης της ενέργειας του μαγνητικού πεδίου του πηνίου είναι dU_L/dt = E²/4R όπου R η αντίσταση κάθε λαμπτήρα τότε:

α. Ο Λ₁ φωτοβολεί πιο έντονα από τους Λ₂ και Λ₃ που φωτοβολούν το ίδιο.

γ. Οι Λ₂ και Λ₃ φωτοβολούν το ίδιο και ο Λ₁ λιγότερο από τους Λ₂ και Λ₃.

Όλοι οι λαμπτήρες συμπεριφέρονται ως ωμικοί αντιστάτες και η φωτοβολία είναι ανάλογη της ισχύος τους.

Θεωρούμε το κύκλωμα του σχήματος όπου R₁ = 4Ω, R₂ = 2Ω, E = 12V, r = 0, L = 0,1 H ο διακόπτης αρχικά είναι ανοικτός και τη στιγμή t = 0 κλείνουμε αυτόν.

i) Να βρεθεί η ενέργεια που έχει αποθηκευτεί στο μαγνητικό πεδίο του πηνίου.

ii) Σε μια στιγμή t₀=0 κλείνουμε το διακόπτη δ.

α) Να βρεθεί η τάση στα άκρα κάθε αντιστάτη και η τάση στα άκρα του πηνίου, αμέσως μετά το κλείσιμο του διακόπτη, καθώς και τη στιγμή t₁ που η ένταση του ρεύματος έχει την τιμή i₁=5Α.

β) Ποια η ισχύς της πηγής και του πηνίου τις δυο παραπάνω χρονικές στιγμές;

iii) Αφού σταθεροποιηθεί ξανά η ένταση του ρεύματος, την στιγμή t₂ ανοίγουμε το διακόπτη δ. Να υπολογιστεί η ισχύς της πηγής, η ισχύς κάθε αντιστάτη και η ισχύς του πηνίου, αμέσως μετά το άνοιγμα του διακόπτη.

ο διακόπτης δ είναι ανοικτός, να υπολογισθούν τα ρεύματα που διαρρέουν τους κλάδους του κυκλώματος

(β) όταν το ρεύμα που διαρρέει την μπαταρία έχει ένταση 0,5 Α , di/dt = ;

(γ) μετά από αρκετό χρόνο μετά το κλείσιμο του διακόπτη δ

ανοίγει ο διακόπτης δ , να υπολογισθούν τα ρεύματα που διαρρέουν τους κλάδους του κυκλώματος (i) αμέσως μετά , (ii) μετά από αρκετό χρόνο di/dt = ;

(a) t = 0 I₀ = E / (R₁ + R₂) = 12 / (10 + 20) = 12 / 30 = 0,4 A I_L = 0

(b) E - L di/dt = i R₂ => 12 V - 0,01 di/dt = 0,5 20 => 0,01 di/dt = 2 V => di/dt = 2 / 0,01 = 200 A/s

L di_L /dt = i₁ R₁ => 2 V = i₁ 10 => i₁ = 0,2 A i_L = 0,5 A - 0,2 A = 0,3 A

(5) κλείνει ο διακόπτης δ : i = i₁ + i_L L di_L /dt = i₁ R₁ E = i R₂ + i₁ R₁

=> E - L di_L /dt = ( i₁ + i_L ) R₂ => E - L di_L /dt = ( L/R₁ di_L /dt + i_L ) R₂ =>

=> E - L di_L /dt = LR₂/R₁ di_L /dt + i_L R₂ => - L di_L /dt - LR₂/R₁ di_L /dt = i_L R₂ - E =>

=> - L ( 1 + R₂/R₁ ) di_L /dt = R₂ ( i_L - E/R₂ ) => di_L / ( i_L - E/R₂ ) = - R₂ / L( 1 + R₂/R₁ ) dt =>

=> ln[ ( i_L - E/R₂ )/ (- E/R₂ ) ] = - R₁R₂ / L(R₁ + R₂) t => ( i_L - E/R₂ )/ (- E/R₂ ) = e^{- R₁R₂ / L(R₁ + R₂) t} =>

=> i_L (t) = E/R₂ [ 1 - e^{- R₁R₂ / L(R₁ + R₂) t} ] i_L (0) = E/R₂ [ 1 - e⁰ ] = 0 i_L (¥) = E/R₂

i_L (t) = E/R₂ [ 1 - e^{- R₁R₂ / L(R₁ + R₂) t} ] => di_L /dt = - E/R₂ [ - R₁R₂ / L(R₁ + R₂) ] e^{- R₁R₂ / L(R₁ + R₂) t} =>

i₁(t) = L/R₁ di_L /dt = E/(R₁ + R₂) e^{- R₁R₂ / L(R₁ + R₂) t}

i = i₁ + i_L = E/(R₁ + R₂) e^{- R₁R₂ / L(R₁ + R₂) t} + E/R₂ [ 1 - e^{- R₁R₂ / L(R₁ + R₂) t} ] =

= E/R₂ + ( E/(R₁ + R₂) - E/R₂ ) e^{- R₁R₂ / L(R₁ + R₂) t} => i(t) = E/R₂ - ER₁ /(R₁ + R₂)R₂ ^. e^{- R₁R₂ / L(R₁ + R₂) t}

i_L(t) = 12/20 [ 1 - e^{-200/ (0,01 30) .t} ] = 0,6 [ 1 - e^{-2000/3 .t} ]

di_L /dt = ER₁/ L(R₁ + R₂) e^{- R₁R₂ / L(R₁ + R₂) t} = 12 10 / (0,01 30) e^{-200/ (0,01 30) .t} = 400 e^{-2000/3 .t}

i(t) = 12/20 - (12 10) / (30 20) ^. e^-2000/3 t = 0,6 - 0,2 ^. e^-2000/3 t = i_L(t) + i₁(t)

i_L0) = 0,6 [ 1 - e⁰ ] = 0 di_L /dt = 400 Α/s , i_L (¥) = 0,6 A di_L /dt = 0

0,6 - 0,2 ^. e^-2000/3 t = 0,5 => 0,6 - 0,5 = 0,2 ^. e^-2000/3 t => 0,1 = 0,2 ^. e^-2000/3 t => 1/2 = e^-2000/3 t =>

i_L = 0,6 [ 1 - e^{-2000/3 .t} ] = 0,6 [ 1 - 1/2 ] = 0,3 A i = i_L + i₁ = 0,3 A + 0,2 A = 0,5 A

i(t) = 0,6 - 0,2 ^. e^-2000/3 t = 0,5 => 0,2 ^. e^-2000/3 t = 0,6 - 0,5 = 0,1 => e^-2000/3 t = 0,5

E - L di_L /dt = i R₂ => 12 - 0,01 di_L /dt = 0,5 20 => di_L /dt = (12 - 10) / 0,01 = 200 A/s E = i R₂ + i₁ R₁ => 12 = 0,5 20 + i₁ 10 => i₁ = (12 - 10) / 10 = 0,2 A

- L di/dt = i R₁ => L di/dt = - i R₁ => di / i = - R₁/L dt => ln( i / Ι ) = -R₁/L^.t =>

t = 0 i = 0,6 A - L di/dt = i R₁ => - 0,01 di/dt = 0,6 10 => di/dt = - 600 A/s

(1) E - L di/dt = i (R + r) => - 0,2 di/dt = i 10 - 12 => - 0,2 di/dt = 10 (i - 1,2) => di / (i - 1,2) = - 50 dt => ln { (i - 1,2) / (- 1,2) } = - 50 t => i - 1,2 = - 1,2 e^-50t => i(t) = 1,2 (1 - e^-50t) di/dt = 60 e^-50t

i(0) = 0 αρχική τιμή του ρεύματος i(¥) = 1,2 Α = I₀ τελική τιμή του ρεύματος

di(t)/dt = 60 e^-50t t=0 di/dt = 60 A/s αρχικός ρυθμός μεταβολής της εντάσεως του ρεύματος

V_πολική = Ε - i r = 12 - 1,2 (1 - e^-50t) 2 = 9,6 + 2,4 e^-50t t = 0 V_πολική = 12 V t ® ¥ V_πολική = 9,6 V

i R = 1,2 (1 - e^-50t) 8 = 9,6 (1 - e^-50t) (1) L di/dt = 0,2 60 e^-50t = 12 e^-50t (2) (1) + (2) = 9,6 + 2,4 e^-50t

t = 0 i R = 0 V t ® ¥ i R = 9,6 V t = 0 L di/dt = 12 V t ® ¥ L di/dt = 0 V

Ρ_πηγής = Ε i = 12 V 0,2 A = 2,4 Watt P_r = i² r = 0,2² 2 = 0,08 W P_R = i² R = 0,2² 8 = 0,32 W

(2) t = 0 E = I₀ (r + R) => 12 V = I₀ 10 Ohm => I₀ = 1,2 A αρχική τιμή του ρεύματος t = 0

- L di/dt = i R => - 0,1 di/dt = i 9 => - 0,1 di/dt = 9 i => di / i = - 90 dt =>

i(0) = 1,2 A = I₀ αρχική τιμή του ρεύματος i(¥) = 0 τελική τιμή του ρεύματος

Ε_ΑΥΤ = - L di/dt = I₀ R = 1,2 A 9 Ω = 10,8 Volt = 12 V - 1,2 V = E - I₀ r

i(t) = 1,2 e^-90t di/dt = - 108 e^-90t t = 0 di/dt = - 108 A/s t = ¥ di/dt = 0

Ε_ΑΥΤ = - L di/dt = i R = 0,5 9 = 4,5 V di/dt = - E_AYT / L = - 4,5 V / 0,1 H = - 45 A/s

(3) E - L di₁/dt = i₁ R (1) E = i₂ 2R => i₂ = E / 2R (2) i = i₁ + i₂ (3)

E - L di₁/dt = i₁ R => - L di₁/dt = i₁ R - E => - L di₁/dt = R ( i₁ - E/R ) => di₁ / ( i₁ - E/R ) = - R/L dt =>

=> ln { ( i₁ - E/R ) / (- E/R) } = - R/L t => ( i₁ - E/R ) = (- E/R) e^{-R/L t} => i₁ (t) = E/R ( 1 - e^{-R/L t} )

U_L = 0,5 L i₁² dU_L / dt = L i₁ di₁/dt = L E/R ( 1 - e^{-R/L t} ) E/L e^{-R/L t} = E² /R ( 1 - e^{-R/L t} ) e^{-R/L t}

dU_L / dt = E² / 4R => E² /R ( 1 - e^{-R/L t} ) e^{-R/L t} = E² / 4R => ( 1 - e^{-R/L t} ) e^{-R/L t} = 1/4 =>

=> e^{-2R/L t} - e^{-R/L t} + 1/4 = 0 τριώνυμο Δ = 1 - 4 1/4 = 0 e^{-R/L t} = 1/2

οπότε i₁ = E/R ( 1 - e^{-R/L t} ) = E/R ( 1 - 1/2 ) = E / 2R = i₂ από σχέση (2)

dU_L / dt = L i₁ di₁/dt => E² / 4R = i₁ ( Ε - i₁ R ) => E² / 4R = E i₁ - i₁² R => E² - 4R E i₁ + i₁² 4R² = 0 => ( 2R i₁ - E )² = 0 => i₁ = E / 2R = i₂

(4) t = 0 E = I (R₁ + R₂) => 12 = I 6 => I = 2A U_L = ½ L I² = ½ 0,1 2² = 0,2 J

όταν κλείσουμε τον διακόπτη βρχυκυκλώνουμε την αντίσταση R₁ οπότε μεταβάλλεται η ένταση του ρεύματος που διαρρέει το πηνίο άρα μεταβάλλεται η ένταση του μαγνητικού πεδίου στο εσωτερικό του πηνίου με συνέπεια να μεταβάλλεται η μαγνητική ροή και εμφανίζεται επαγωγική τάση στα άκρα του πηνίου E - L di/dt = Ι R₂ => 12 - L di/dt = 2 2 => - L di/dt = Ε_αυτεπ = - 8V αντίθετη πολικότητα από την πηγή

E - L di/dt = i R₂ => 12 - 0,1 di/dt = i 2 => - 0,1 di/dt = 2 (i - 6) => di / (i - 6) = - 20 dt =>

=> ln [ (i - 6) / (2 - 6) ] = - 20 t => i - 6 = - 4 e^-20t => i(t) = 6 - 4 e^-20t di/dt = 80 e^-20t

i(t) = 6 - 4 e^-20t = 5A => 4 e^-20t = 6 - 5 = 1 => e^-20t = 1/4 => 20t = ln4 => t = 0,1 ln2 s

P_L = L i di/dt = 0,1 ( 6 - 4 e^-20t ) 80 e^-20t = 8 e^-20t ( 6 - 4 e^-20t ) = 8 1/4 5 = 10 J/s

E - L di/dt = i (R₁ + R₂) => 12 - 0,1 di/dt = i 6 => - 0,1 di/dt = 6 (i - 2) =>

=> di / (i - 2) = - 60 dt => ln [ (i - 2) / (6 - 2) ] = - 60 t => i - 2 = 4 e^-60t => i(t) = 2 + 4 e^-60t