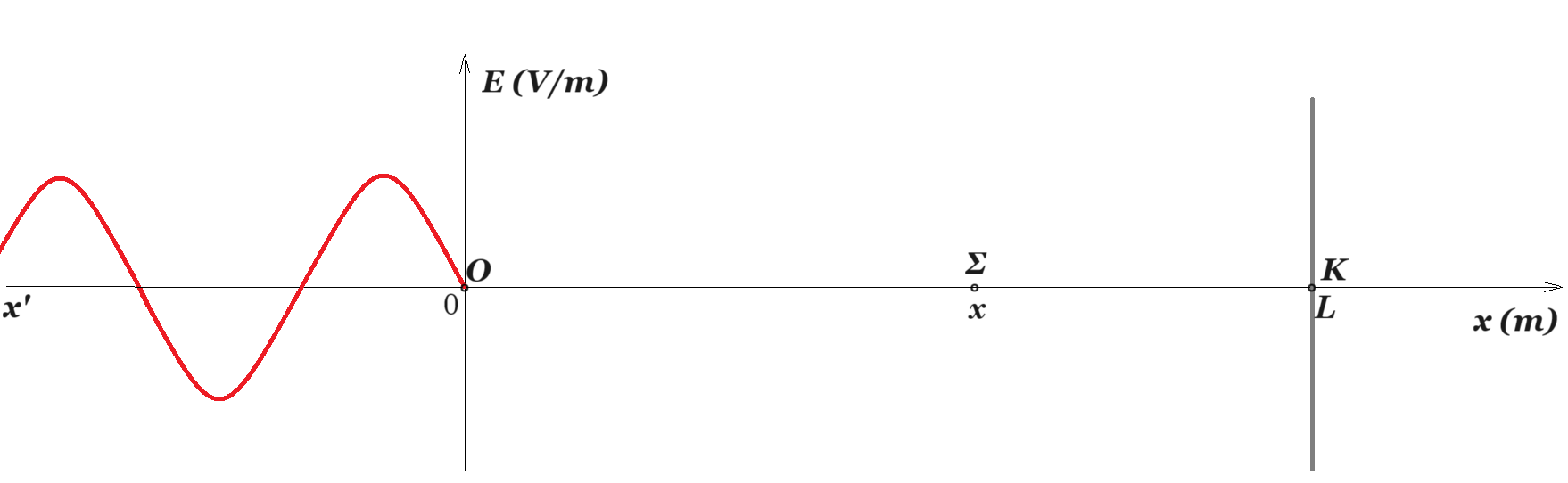 Εγκάρσιο Η/Μ κύμα διαδίδεται στον χώρο φθάνοντας τη χρονική στιγμή t=0 στο σημείο Ο(0,0) το οποίο θεωρούμε ως αρχή των συντεταγμένων. Το κύμα διαδίδεται από αριστερά προς τα δεξιά επάνω στον άξονα x'x. Στο σχήμα φαίνεται η ένταση του ηλεκτρικού πεδίου συναρτήσει της απόστασης. Θεωρούμε τυχαίο σημείο Σ στη θέση x. Η εξίσωση του κύματος για το Σ είναι :
Εγκάρσιο Η/Μ κύμα διαδίδεται στον χώρο φθάνοντας τη χρονική στιγμή t=0 στο σημείο Ο(0,0) το οποίο θεωρούμε ως αρχή των συντεταγμένων. Το κύμα διαδίδεται από αριστερά προς τα δεξιά επάνω στον άξονα x'x. Στο σχήμα φαίνεται η ένταση του ηλεκτρικού πεδίου συναρτήσει της απόστασης. Θεωρούμε τυχαίο σημείο Σ στη θέση x. Η εξίσωση του κύματος για το Σ είναι :
Ε1,Σ (x,t) = E0 ημ(2πt/Τ - 2πx/λ) t > x/v λ/Τ = v ταχύτητα διαδόσεως του κύματος στο μέσο.
Το κύμα προσπίπτει κάθετα σε επίπεδη επιφάνεια στο σημείο της Κ το οποίο απέχει απόσταση L από το σημείο Ο. Το σημείο Κ είναι σταθερό σημείο οπότε το κύμα ανακλάται και στο σημείο Κ υφίσταται διαφορά φάσης π rad.
Η εξίσωση του κύματος που φθάνει στο Κ είναι : Ε1,Κ (x=L,t) = E0 ημ(2πt/Τ - 2πL/λ) t > L/v
το ανακλώμενο κύμα στο σημείο Κ θα έχει εξίσωση κύματος : Ε'1,Κ (x,t) = E0 ημ(2πt/Τ - 2πL/λ + π)
το σημείο Σ απέχει από το Κ απόσταση L - x το ανακλώμενο κύμα χρειάζεται χρόνο (L - x)/υ για να φθάσει από το Κ στο Σ
θα έχει εξίσωση κύματος : Ε2,Σ (x,t) = E0 η[2π(t - (L - x)/υ)/Τ - 2πL/λ + π ] =
= E0 ημ[2π(t - L/υ + x/υ)/Τ - 2πL/λ + π ] = t > (L - x)/v + L/v = 2L/v - x/v
= E0 ημ[2πt/Τ - 2πL/υΤ + 2πx/υΤ - 2πL/λ + π ] =>
=> Ε2,Σ (x,t) = E0 ημ(2πt/Τ + 2πx/λ - 4πL/λ + π )
Στο σημείο Σ φθάνουν δύο κύματα οπότε συμβαίνει συμβολή το συνολικό θα είναι :
Ε1,Σ (x,t) + Ε2,Σ (x,t) = E0 ημ(2πt/Τ - 2πx/λ) + E0 ημ(2πt/Τ + 2πx/λ - 4πL/λ + π ) =
= 2E0 ημ( 2πt/Τ - 2πx/λ + 2πt/Τ + 2πx/λ - 4πL/λ + π ) / 2 συν( 2πt/Τ - 2πx/λ - 2πt/Τ - 2πx/λ + 4πL/λ - π ) / 2
= 2E0 ημ( 2πt/Τ - 2πL/λ + π/2 ) συν( - 2πx/λ + 2πL/λ - π/2 ) t > (L - x)/v + L/v = 2L/v - x/v
ΕΣ, στάσιμο κύμα (x,t) = 2E0 συν( - 2πx/λ + 2πL/λ - π/2 ) ημ( 2πt/Τ - 2πL/λ + π/2 )
μετά από την χρονική στιγμή t1 = 2L/v μεταξύ των σημείων Ο και Κ επικρατεί στάσιμο κύμα
υπάρχουν σημεία που είναι δεσμοί και σημεία κοιλίες
ΚΟΙΛΙΕΣ :
συν( - 2πx/λ + 2πL/λ - π/2 ) = ± 1 = συν(π) ή συν(0) => - 2πx/λ + 2πL/λ - π/2 = Ν.π =>
=> - 2x/λ + 2L/λ - 1/2 = Ν => 2x = 2L - λ/2 - Ν.λ => x = L - λ/4 - Ν.λ/2 δεσμοί
αλλά 0 £ x £ L => 0 £ L - λ/4 - Ν.λ/2 £ L => - L + λ/4 £ - Ν.λ/2 £ L - L + λ/4 =>
=> 2L/λ - 1/2 > Ν > - 1/2 => - 0,5 £ Ν £ 2L/λ - 0,5
λ = 2m L = 3m - 0,5 £ N £ 2,5 N = 0, 1, 2 x = 2,5m , 1,5m , 0,5m
ΔΕΣΜΟΙ :
συν( - 2πx/λ + 2πL/λ - π/2 ) = 0 = συν(π/2) ή συν(3π/2) => - 2πx/λ + 2πL/λ - π/2 = Ν.π + π/2 =>
=> - 2x/λ + 2L/λ = Ν + 1 => 2x = 2L - Ν.λ - λ => x = L - λ/2 - Ν.λ/2 κοιλίες
αλλά 0 £ x £ L => 0 £ L - λ/2 - Ν.λ/2 £ L => - L + λ/2 £ - Ν.λ/2 £ L - L + λ/2 =>
=> 2L/λ - 1 > Ν > - 1 => - 1 £ Ν £ 2L/λ - 1
λ = 2m L = 3m - 1 £ N £ 2 N = -1, 0, 1, 2 x = 3m (σημείο Κ) , 2m , 1m , 0m (σημείο Ο)
Ηλεκτρομαγνητικό κύμα
Ε(x,t) = E0 ημ2π( ft - x/λ ) Β(x,t) = Β0 ημ2π( ft - x/λ ) Ε = Β c στο κενό
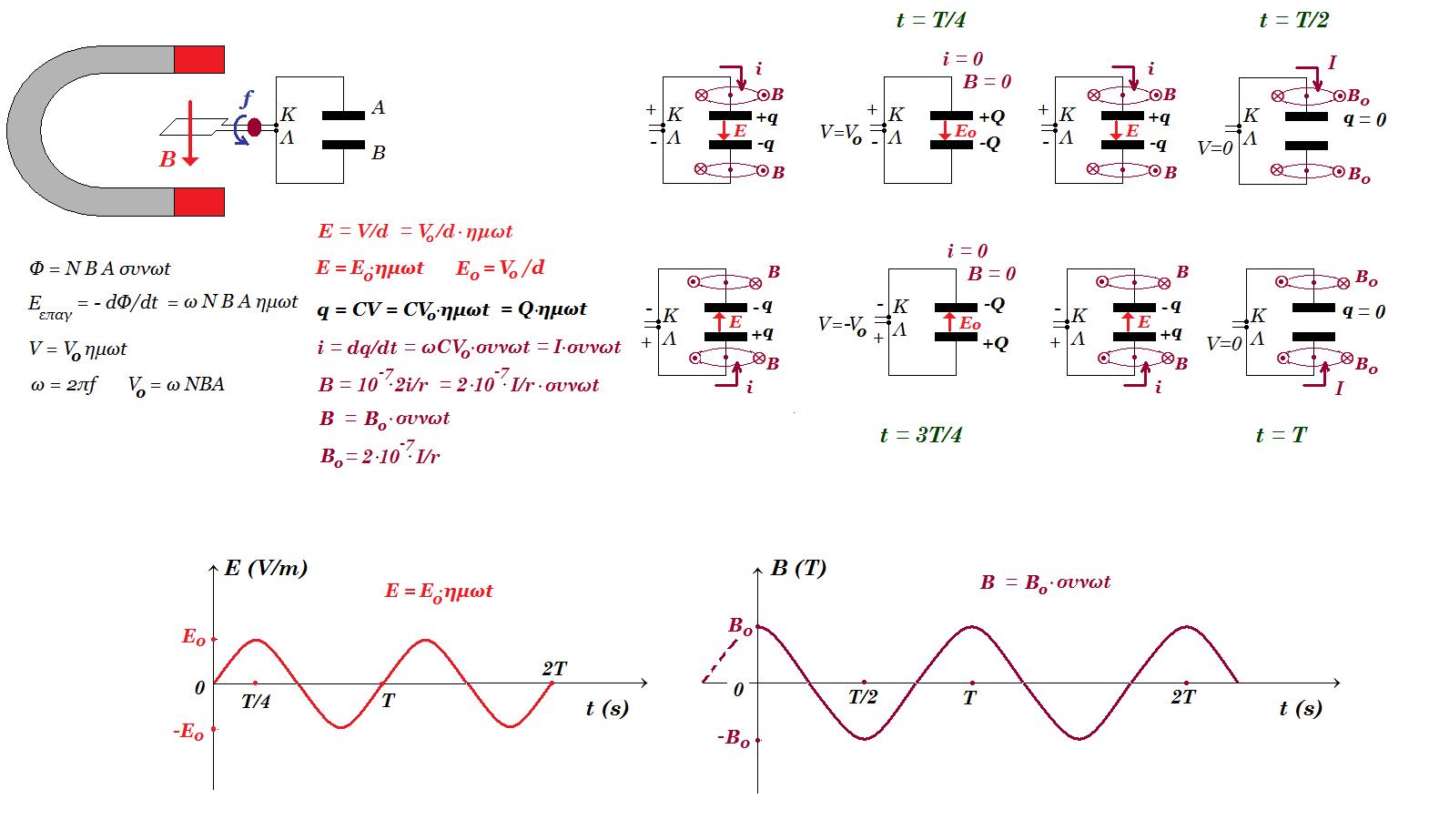
Μεταλλικό πλαίσιο μηδενικής ωμικής αντίστασης, με εμβαδόν επιφάνειας Α, φέρει Ν σπείρες, στρέφεται μέσα σε ομογενές μαγνητικό πεδίο εντάσεως Β του οποίου οι δυναμικές γραμμές είναι κάθετες στον άξονα του πλαισίου. Αρχικά η επιφάνεια του πλαισίου είναι κάθετη στις δυναμικές γραμμές του πεδίου. Τα άκρα Κ, Λ του πλαισίου συνδέονται με καλώδια μηδενικής ωμικής αντίστασης με δύo αγωγούς Α και Β, αφόρτιστους, που απέχουν απόσταση d. Περιστρέφουμε το πλαίσιο με σταθερή γωνιακή ταχύτητα ω. Η μαγνητική ροή που διέρχεται μέσα από την επιφάνεια του πλαισίου, των δυναμικών γραμμών του πεδίου δίνεται από τη σχέση : Φ = N B A συνθ = Ν Α Β συνωt. ( t = 0 => συνωt = 1 => Φ = N B A μέγιστη ροή ). Επειδή η γωνία θ μεταβάλλεται με το χρόνο τότε μεταβάλλεται η ροή Φ και εμφανίζεται επαγωγική τάση στα άκρα Κ Λ του πλαισίου. Eεπαγ = - ΔΦ/Δt = - dΦ/dt = - N B A ( συνωt )' = ω Ν Β Α ημωt. Η τάση αυτή μεταβάλλεται αρμονικά ( ημιτονοειδώς ) με το χρόνο είναι εναλλασσόμενη τάση : V = V0 ημωt όπου V0 = ω Ν Β Α είναι η μέγιστη τάση ( πλάτος τάσης ). Μεταξύ των αγωγών Α και Β δημιουργείται ηλεκτρικό πεδίο με ένταση Ε = V / d = V0/d ημωt .
Τη στιγμή t = 0 η τάση είναι μηδέν αμέσως μετά το άκρο Κ του πλαισίου αποκτά έστω θετικό δυναμικό και το άκρο Λ αποκτά αρνητικό. Ηλεκτρόνια κινούνται από το Λ προς τον αγωγό Β και από τον αγωγό Α προς το άκρο Κ. Δημιουργείται ρεύμα εντάσεως i με συνέπεια μαγνητικό πεδίο. Σε απόσταση r η ένταση του μαγνητικού πεδίου είναι : Β = 10-7 2i/r . Tη στιγμή t=T/4 μεταξύ των άκρων Κ, Λ επικρατεί μέγιστη τάση V0 , η ένταση του ηλεκτρικού πεδίου γίνεται μέγιστη Ε0 και οι αγωγοί Α , Β αποκτούν μέγιστο φορτίο Q, με συνέπεια το ρεύμα να μηδενίζεται.
Αμέσως μετά μειώνεται η τάση στα άκρα Κ και Λ, όχι η πολικότητα, με συνέπεια να μειώνεται το φορτίο q στους αγωγούς Α και Β άρα μειώνεται η τάση στους αγωγούς Α και Β άρα μειώνεται η ένταση Ε του ηλεκτρικού πεδίου, τα καλώδια διαρρέονται από ρεύμα έντασης i ίδιας φοράς μέχρι τη στιγμή t=T/2 όπου μηδενίζεται η τάση μεταξύ των άκρων Κ, Λ άρα μηδενίζεται το φορτίο άρα μηδενίζεται η ένταση του ηλεκτρικού πεδίου, ενώ η ένταση του ρεύματος γίνεται Ι μέγιστη με συνέπεια η ένταση του μαγνητικού πεδίου να γίνεται μέγιστη Β0 .
Αμέσως μετά αλλάζει η πολικότητα των άκρων Κ και Λ ( το Κ φορτίζεται αρνητικά και το Λ θετικά ) τα ηλεκτρόνια κινούνται από το άκρο Κ προς τον αγωγό Α και από τον αγωγό Β προς το άκρο Λ ( δηλαδή κινούνται αντίθετα απ' ότι προηγουμένως ), αυξάνεται η τάση, αυξάνεται το φορτίο, αυξάνεται η τάση μεταξύ των αγωγών Α, Β συνεπώς αυξάνεται η ένταση Ε του ηλεκτρικού πεδίου μεταξύ των αγωγών Α, Β ( έχει αντίθετη κατεύθυνση απ' ότι προηγουμένως ) , επειδή τα ηλεκτρόνια κινούνται αντίθετα απ' ότι προηγουμένως η φορά του ρεύματος είναι αντίθετη απ' ότι προηγουμένως και συνεχώς μειώνεται η ένταση του i συνεπώς μειώνεται η ένταση Β του μαγνητικού πεδίου ( η φορά είναι αντίθετη απ' ότι προηγουμένως ) μέχρι τη t=3T/4 όπου μεταξύ των άκρων Κ, Λ επικρατεί μέγιστη τάση -V0 και οι αγωγοί Α , Β αποκτούν μέγιστο φορτίο Q, η ένταση του ηλεκτρικού πεδίου γίνεται μέγιστη -Ε0 με συνέπεια το ρεύμα να μηδενίζεται καθώς και η ένταση του μαγνητικού πεδίου.
Αμέσως μετά μειώνεται η τάση στα άκρα Κ και Λ, όχι η πολικότητα, με συνέπεια να μειώνεται το φορτίο q στους αγωγούς Α και Β άρα μειώνεται η τάση στους αγωγούς Α και Β άρα μειώνεται η ένταση Ε του ηλεκτρικού πεδίου, τα καλώδια διαρρέονται από ρεύμα ίδιας φοράς αυξάνεται η ένταση i μέχρι τη στιγμή t=T όπου μηδενίζεται η τάση μεταξύ των άκρων Κ, Λ άρα μηδενίζεται το φορτίο άρα μηδενίζεται η ένταση του ηλεκτρικού πεδίου, ενώ η ένταση του ρεύματος γίνεται Ι μέγιστη με συνέπεια η ένταση του μαγνητικού πεδίου να γίνεται μέγιστη Β0 .
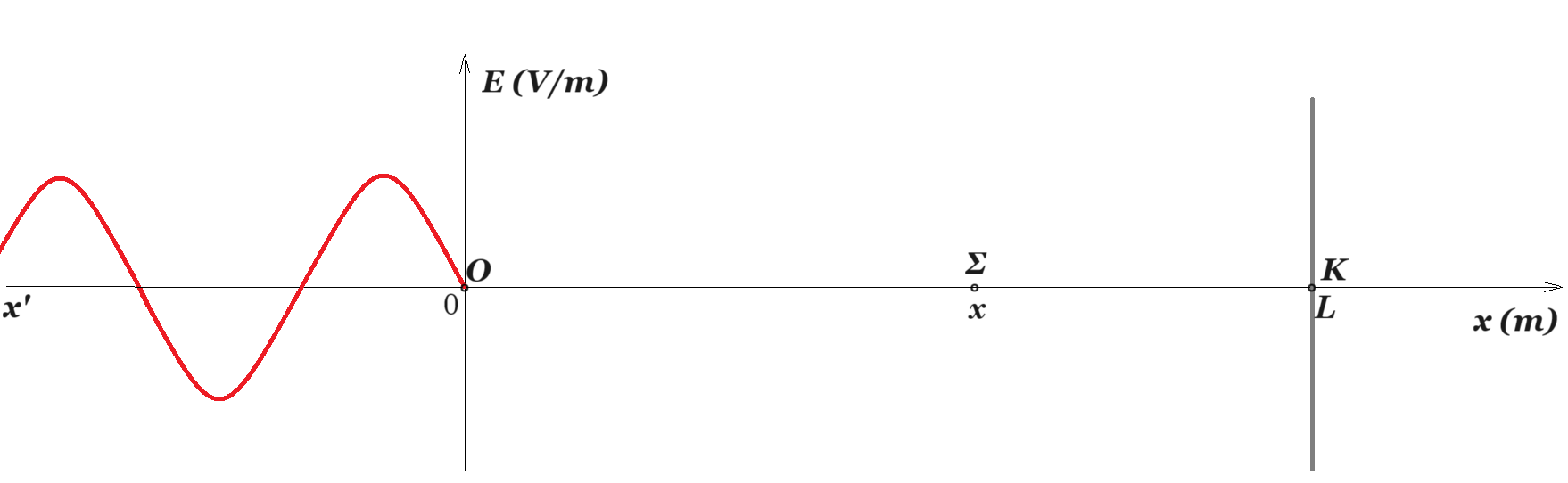 Εγκάρσιο Η/Μ κύμα διαδίδεται στον χώρο φθάνοντας τη χρονική στιγμή t=0 στο σημείο Ο(0,0) το οποίο θεωρούμε ως αρχή των συντεταγμένων. Το κύμα διαδίδεται από αριστερά προς τα δεξιά επάνω στον άξονα x'x. Στο σχήμα φαίνεται η ένταση του ηλεκτρικού πεδίου συναρτήσει της απόστασης. Θεωρούμε τυχαίο σημείο Σ στη θέση x. Η εξίσωση του κύματος για το Σ είναι :
Εγκάρσιο Η/Μ κύμα διαδίδεται στον χώρο φθάνοντας τη χρονική στιγμή t=0 στο σημείο Ο(0,0) το οποίο θεωρούμε ως αρχή των συντεταγμένων. Το κύμα διαδίδεται από αριστερά προς τα δεξιά επάνω στον άξονα x'x. Στο σχήμα φαίνεται η ένταση του ηλεκτρικού πεδίου συναρτήσει της απόστασης. Θεωρούμε τυχαίο σημείο Σ στη θέση x. Η εξίσωση του κύματος για το Σ είναι : 