ΘΕΜΑ  A1.   

H εξίσωση που περιγράφει την ένταση του ηλεκτρικού πεδίου σε ένα ηλεκτρομαγνητικό κύμα είναι,  Ε = 0,03 ημ(2π·10¹⁵t − 2π·10⁷x/3) (SI).
α.  Να γραφεί η εξίσωση που περιγράφει την ένταση του μαγνητικού πεδίου.
β.  Να εξεταστεί αν το κύμα αυτό ανήκει στην ορατή περιοχή του φάσματος.
γ.  Να υπολογιστεί η διαφορά φάσης Δφ μεταξύ δύο σημείων που απέχουν μεταξύ τους απόσταση  Δx=4,5·10⁻⁷ m, την ίδια χρονική στιγμή.
δ.  Να βρεθεί η απόσταση x που έχει φτάσει το κύμα τη χρονική στιγμή, t=500s.
ε.  Να σχεδιαστεί στιγμιότυπο του ηλεκτρικού κύματος τη χρονική στιγμή t=2·10⁻¹⁵ s.

...........................................................................................................................................................................

ΘΕΜΑ  Α2.   

Ηλεκτρομαγνητικό κύμα συχνότητας f  ταξιδεύει στον αέρα με ταχύτητα  c = 3·10⁸ m/s  προσπίπτει κάθετα  σε κατακόρυφο τοίχο (σημείο Ο)  και ανακλάται χωρίς απώλειες ενέργειας.  Σχηματίζεται στάσιμο κύμα με δεσμό στον τοίχο.  Η πρώτη από το εμπόδιο κοιλία απέχει από τον τέταρτο δεσμό, απόσταση  d = 5·10⁻² m.  Μετρήθηκε η μέγιστη τιμή της έντασης του μαγνητικού πεδίου  του στασίμου κύματος :  8·10⁻⁷ Τ.

 α.   Να βρεθεί η συχνότητα της ακτινοβολίας.

 β.   Να γραφούν οι εξισώσεις ως προς x και t που περιγράφουν τις εντάσεις ηλεκτρικού και μαγνητικού πεδίου.        

 γ.  Να γραφούν οι εξισώσεις ως προς x και t που περιγράφουν τις εντάσεις ηλεκτρικού και μαγνητικού πεδίου για το στάσιμο κύμα.   Θεωρούμε αρχή x = 0  το σημείο προσπτώσεως Ο.       

...........................................................................................................................................................................

ΘΕΜΑ  Γ.

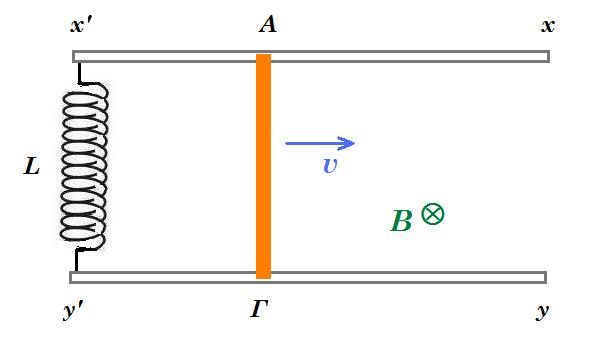
Ο αγωγός ΑΓ, μήκους l=1m, μάζας m=2kg έχει αντίσταση R=4Ω και κινείται οριζόντια σε επαφή με δύο ευθύγραμμους αγωγούς x΄x και y΄y, οι οποίοι δεν παρουσιάζουν αντίσταση και απέχουν κατά l, ενώ στα άκρα τους x΄και y΄ συνδέεται ένα ιδανικό πηνίο, με συντελεστή αυτεπαγωγής L=0,2 Η. Το όλον σύστημα βρίσκεται μέσα σε ένα κατακόρυφο ομογενές μαγνητικό πεδίο έντασης Β=1Τ, όπως στο σχήμα. Μια χρονική στιγμή t₁, ο αγωγός ΑΓ έχει ταχύτητα υ₁=2m/s, με φορά προς τα δεξιά, ενώ η τάση στα άκρα του είναι ίση με V_ΑΓ=0,4V.  Για την στιγμή αυτή ζητούνται:

α)   Η ένταση του ρεύματος που διαρρέει το κύκλωμα  και  ο ρυθμός μεταβολής της έντασης di/dt.

β)   Ο ρυθμός μεταβολής της κινητικής ενέργειας του αγωγού ΑΓ. Ποια η αντίστοιχη ηλεκτρική ισχύς του ρεύματος που διαρρέει το κύκλωμα;

γ)   Η ενέργεια του μαγνητικού πεδίου του πηνίου  και  ο ρυθμός μεταβολής της ενέργειας αυτής.

.........................................................................................................................................................................

ΘΕΜΑ  Δ.

Οι οριζόντιοι αγωγοί ΓΜ και ΔΝ του σχήματος έχουν ασήμαντη αντίσταση και πολύ μεγάλος μήκος. Τα άκρα τους Γ και Δ συνδέονται με αντίσταση R₂ = 8Ω. Στο επίπεδο των δύο αγωγών είναι τοποθετημένος κάθετα προς τη διεύθυνση τους ευθύγραμμος αγωγός ΚΛ μήκους l = 0,5m, ο οποίος μπορεί να ολισθαίνει χωρίς τριβές. Η μάζα του αγωγού ΚΛ είναι m = 0,1kg και η αντίσταση του R₁ = 2Ω. Το σύστημα των τριών αγωγών βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο, του οποίου η ένταση μέτρου Β = 2T είναι κάθετη στο επίπεδο των αγωγών. Τη χρονική στιγμή t₀ = 0 εκτοξεύουμε τον αγωγό ΚΛ με οριζόντια αρχική ταχύτητα υ₀ παράλληλη προς τους αγωγούς ΓΜ και ΔΝ, ενώ ταυτόχρονα του ασκούμε σταθερή δύναμη F ομόρροπη με την αρχική του ταχύτητα, με μέτρο F = 0,5N. Η ισχύς που δαπανά η αντίσταση R₂ τη στιγμή της εκτόξευσης είναι P₂ = 8W.

α.  Να υπολογίσετε την τιμή της αρχικής ταχύτητας  του αγωγού ΚΛ

β.  Να περιγράψετε αναλυτικά το είδος της κίνησης που θα εκτελέσει ο αγωγός ΚΛ και να βρείτε την τιμή της τελικής (οριακής) ταχύτητας που θα αποκτήσει

γ.  Να περιγράψετε τις ενεργειακές μετατροπές, που λαμβάνουν χώρα κατά την κίνηση του αγωγού ΚΛ, από τη στιγμή t₀ = 0 μέχρι τη στιγμή που θα αποκτήσει την οριακή του ταχύτητα

δ.  Να κατασκευάσετε ποιοτικό διάγραμμα της Η.Ε.Δ. από επαγωγή που εμφανίζεται στα άκρα του αγωγού ΚΛ σε συνάρτηση με το χρόνο, από τη στιγμή t₀ = 0 μέχρι τη στιγμή που θα αποκτήσει την οριακή του ταχύτητα

ΘΕΜΑ  Α1.

α. Β=10⁻¹⁰ ημ(2π10¹⁵t − 2π·10⁷x/3) (SI),             β.Οχι  υπεριώδες              γ. Δφ/Δx=2π/λ => Δφ=3π rad,           δ. x=ct=15·10¹⁰m   ε. Ε = 0,03 ημ(2π·10¹⁵ 2·10⁻¹⁵ − 2π·10⁷x/3) = 0,03 ημ(4π − 2π·10⁷x/3) 

ΘΕΜΑ  Α2.

α.  λ + λ/4 = 0,05   f = 7,5·10⁹ Ηz,             β.  Ε(x,t) = 120·ημ2π(7,5·10⁹t − 25x),   Β(x,t) = 4·10⁻⁷·ημ2π(7,5·10⁹t − 25x)   (SI)              γ.  Ε = 240·ημ(50πx)·ημ(15π·10⁹t) ,   Β = 8·10⁻⁷·ημ(50πx)·ημ(15π·10⁹t)   (SI)                   

ΘΕΜΑ  Γ.

  Β l v  -  L di/dt  =  i R  =>   Β l v  -  i R  =  L di/dt  =>  V_ΑΓ  = L di/dt  => 0,4 V =  0,2 H di/dt  =>  di/dt = 2 A/s  

   Β l v  -  L di/dt  =  i R  =>   1  1  2  -   0,2  2  =  i  4  =>  i = 0,4 A   

  dK/dt  =  m v a  =  m  v  F_L/m  =  v  F_L  =  v  B l i  =  2  1  1  0,4  =  0,8 J/s  

  P  =  i²  R  =  0,4²  4  =  0,64 Watt  

U_L  =  0,5  L  i²  =  0,5  0,2  0,4²  =  0,016 J            dU_L /dt  =  L  i  di/dt  =  0,2  0,4  2  =  0,16 J/s   

                0,16 J/s  +  0,64 Watt  =  0,8 J/s  

 τη στιγμή  t = 0  δίνουμε ταχύτητα  υ₀  στην ράβδο ΑΓ  οριζόντια προς τα δεξιά  

  ΣF = m a  =>  - F_L = m a  =>  - B l i  =  m a  =>  i  =  - m.a / B.l  =  - 2 dv/dt             di/dt  =  - 2 d²v/dt²  

Β.l.v  -  L di/dt =  i R  =>   v  +  0,4  d²v/dt²  =  -  8  dv/dt  =>   0,4  d²v/dt² +  8  dv/dt +  v  =  0 

   d²v/dt² +   20  dv/dt +  2,5 υ  =  0             Δ = 20² -  4 2,5  =  400  -  10  = 390            Δ^½  = 19,75

  dv/dt  =  (- 20  ±  19,75) / 2  =  - 0,126   ή   - 19,875

ΘΕΜΑ  Δ.

  Ε_επαγ  =  Β υ l  =  i ( R₁  +  R₂ )  =>  2 T  v  0,5 m  =  i  ( 2 Ω  +  8 Ω )  =>  10 i  =  v  =>   i  =  0,1 v           

  P_R2  =  I² R₂  =>  8 Watt = I² 8 Ω  =>  I = 1 A     αρχική τιμή ρεύματος 

άρα  10 i  =  v  => 10 Ι = v₀  =>  v₀  = 10 m/s    αρχική ταχύτητα αγωγού

  ΣF =  m a  =>  F  -  F_L  =  m a  =>  F  -  B i l  =  m a  =>   0,5  -  2   0,1v  0,5  =  0,1 a  =>  a = 5 - v    αρχικά  την χρονική στιγμή t = 0   v = v₀    a = a₀ = 5 - v₀ = 5 - 10 = - 5 m/s²   

  όταν  α = 0    τότε  v =  5 m/s =  v_ορ   οριακή ταχύτητα αγωγού 

         a  =  5  -  v  =  dv/dt  =>  dv / (5 - v)  =  dt  =>  dv / (v - 5)  =  - dt  =>  ln [ (v - 5 )/( 10 - 5) ]  =  - t  =>

=>  v - 5 = 5 e^-t  =>  v(t) =  5 + 5 e^-t      v(0) = 5 + 5 = 10 m/s        a = dv/dt =>   a(t) = - 5 e^-t   a(0) = - 5m/s²  

   Ε_επαγ  =  Β υ l  =  2T 0,5m  ( 5 + 5 e^-t )  =  5 + 5 e^-t  =  Ε_επαγ(t) 

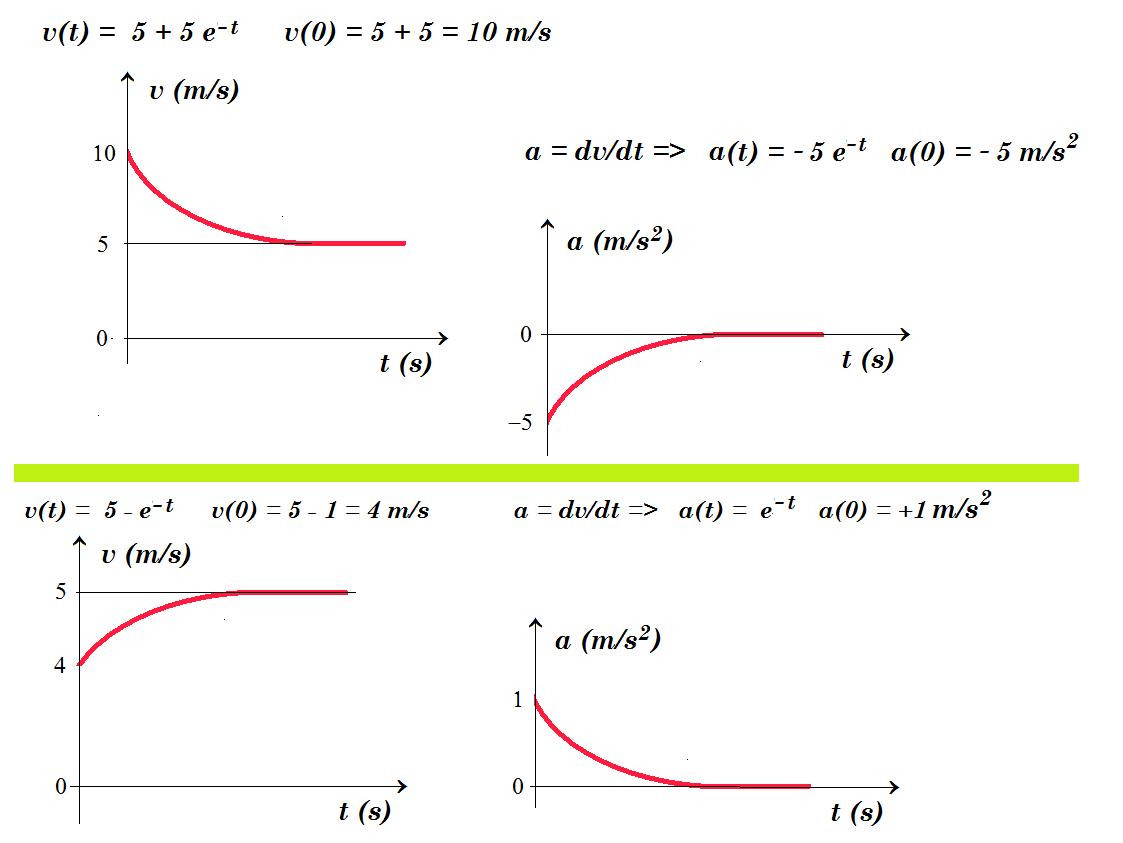
a  =  5  -  v    αρχικά  την χρονική στιγμή t = 0      v = v₀ = 4 m/s            a = a₀ = 5 - v₀ = 5 - 4 = +1 m/s²   

a  =  5 - v  =  dv/dt  =>  dv / (5 - v)  =  dt  =>  dv / (v - 5)  =  - dt  =>  ln [ (v - 5 )/( 4 - 5) ]  =  - t  =>

=>   v - 5 =  -1 e^-t    =>  v(t) =  5 - e^-t      v(0) = 5 - 1 = 4 m/s            a = dv/dt =>   a(t) =  e^-t    a(0) = +1 m/s²