 α) στο κέντρο Ο του κυκλικού βρόχου η ένταση του μαγνητικού πεδίου έχει μέτρο ανάλογο της γωνίας φ και για το ευθύγραμμο σύρμα, στο εσωτερικό του το πεδίο είναι αντιστρόφως ανάλογο της απόστασης r.
α) στο κέντρο Ο του κυκλικού βρόχου η ένταση του μαγνητικού πεδίου έχει μέτρο ανάλογο της γωνίας φ και για το ευθύγραμμο σύρμα, στο εσωτερικό του το πεδίο είναι αντιστρόφως ανάλογο της απόστασης r. ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΨΥΧΙΚΟΥ
ΤΑΞΗ : Γ' ΛΥΚΕΙΟΥ
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ
ΗΜΕΡΟΜΗΝΙΑ : 16 / 5 / 2023 Ονοματεπώνυμο :
ΘΕΜΑΤΑ
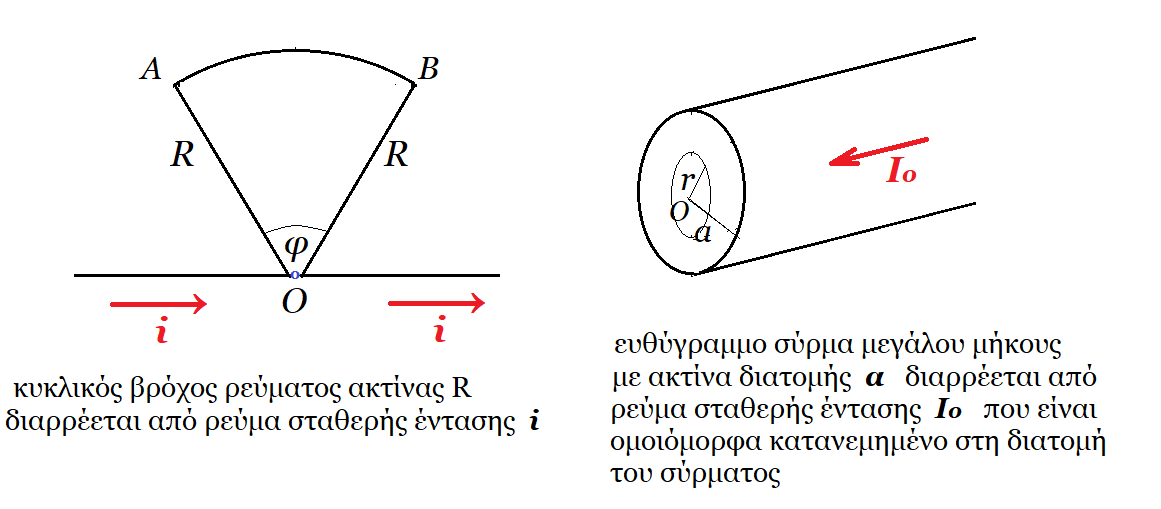
ΘΈΜΑ Α. α) στο κέντρο Ο του κυκλικού βρόχου η ένταση του μαγνητικού πεδίου έχει μέτρο ανάλογο της γωνίας φ και για το ευθύγραμμο σύρμα, στο εσωτερικό του το πεδίο είναι αντιστρόφως ανάλογο της απόστασης r.
α) στο κέντρο Ο του κυκλικού βρόχου η ένταση του μαγνητικού πεδίου έχει μέτρο ανάλογο της γωνίας φ και για το ευθύγραμμο σύρμα, στο εσωτερικό του το πεδίο είναι αντιστρόφως ανάλογο της απόστασης r. Α2.
 |
Στο κύκλωμα του σχήματος μια ηλεκτρική πηγή συνεχούς ρεύματος συνδέεται με μεταβλητή αντίσταση (ροοστάτης) και δύο κλάδους παράλληλους. Ο ένας κλάδος περιλαμβάνει λαμπτήρα με ωμική αντίσταση RΛ και ο άλλος πηνίο με ωμική αντίσταση Rπ ( RΛ > Rπ ). Ο διακόπτης δ είναι κλειστός. |
α) Μετακινούμε τον δρομέα από το άκρο Α του ροοστάτη προς το άκρο Γ σε χρονικό διάστημα Δt.
i) το πηνίο "αντιδρά" και το άκρο του Λ γίνεται βόρειος πόλος
ii) ο λαμπτήρας φωτοβολεί εντονότερα για χρονικό διάστημα Δt
iii) το πηνίο διαρρέεται από ρεύμα μεγαλύτερης έντασης
iv) τίποτα από τα ανωτέρω.
β) Τοποθετούμε τον δρομέα σε ορισμένη θέση έτσι ώστε ο λαμπτήρας να φωτοβολεί ελάχιστα και ανοίγουμε τον διακόπτη.
i) ο λαμπτήρας σβήνει αμέσως
ii) ο λαμπτήρας φωτοβολεί αμυδρά για μικρό χρονικό διάστημα και μετά σβήνει
iii) ο λαμπτήρας αρχικά φωτοβολεί πιο έντονα και μετά σβήνει μετά από κάποιο χρονικό διάστημα ενώ το άκρο Κ του πηνίου είναι βόρειος πόλος κατά το ίδιο χρονικό διάστημα
iv) τίποτα από τα ανωτέρω.
μονάδες 2 + 3
Α3. Σώμα εκτελεί ΑΑΤ, στο σχήμα φαίνεται το διάγραμμα υ(t) της ταχύτητας συναρτήσει του χρόνου.
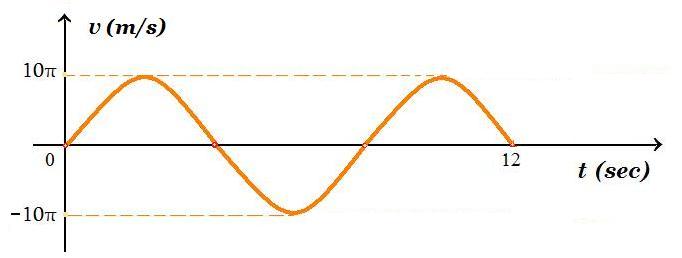 Η εξίσωση της απομάκρυνσης συναρτήσει του χρόνου είναι :
Η εξίσωση της απομάκρυνσης συναρτήσει του χρόνου είναι : 
Α5. Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα την λέξη Σωστό, για την σωστή πρόταση, και την λέξη Λάθος, για την λανθασμένη.
α. Στα άκρα αντίστασης 10 Ω εφαρμόζεται εναλλασσόμενη τάση. Η ισχύς που καταναλώνεται στην αντίσταση φαίνεται στο διάγραμμα P(t). H χρονική εξίσωση του ρεύματος είναι : i(t) = 2∙ημ(5πt).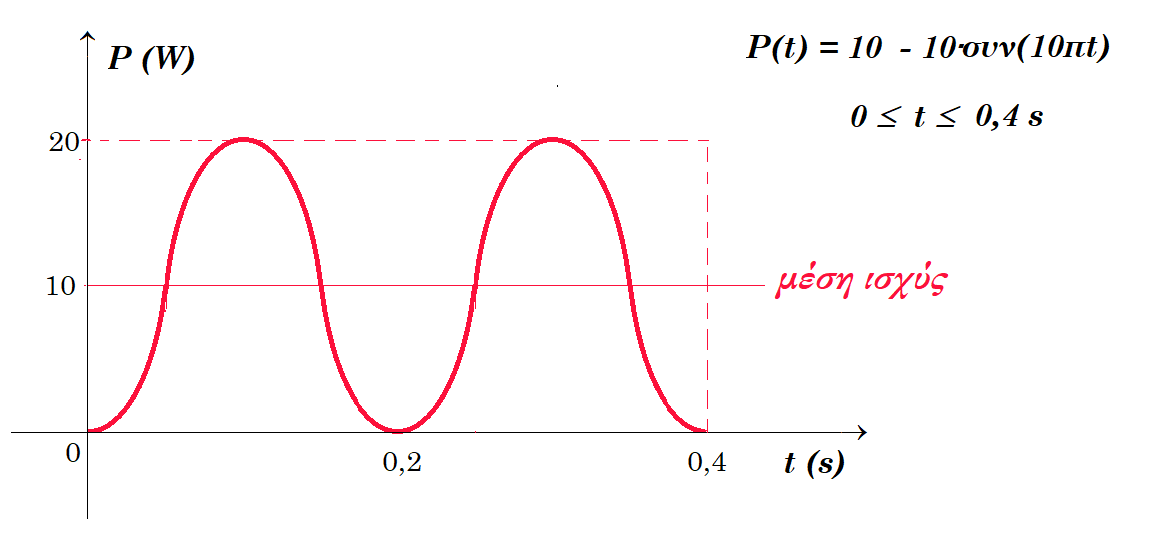 β. Ηλεκτρόνιο είναι η πιθανότητα να βρεθεί κάπου στον χώρο αρνητικό ηλεκτρικό φορτίο κάποια χρονική στιγμή.
β. Ηλεκτρόνιο είναι η πιθανότητα να βρεθεί κάπου στον χώρο αρνητικό ηλεκτρικό φορτίο κάποια χρονική στιγμή.
γ. Ο νόμος του Ampere ισχύει όταν τα ηλεκτρικά ρεύματα είναι εναλλασσόμενα.
δ. Σε χαμηλές θερμοκρασίες το μέλαν σώμα εκπέμπει στο υπέρυθρο.
ε. Ένα ηλεκτρόνιο περιστρέφεται γύρω από συνεχώς ακίνητο πρωτόνιο με σταθερή συχνότητα περιστροφής f σε ακτίνα r. Το διάνυσμα της στροφορμής L του ηλεκτρονίου και το διάνυσμα της έντασης Β του μαγνητικού πεδίου που δημιουργεί, είναι ομόρροπα.
μονάδες 5
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
ΘΈΜΑ B.
B1. Σώμα μάζας m κινούμενο πάνω σε λείο οριζόντιο δάπεδο με ταχύτητα μέτρου υ προσπίπτει κάθετα σε κατακόρυφο τοίχο και ανακλάται με ταχύτητα μέτρου υ'. Αν το μέτρο της μεταβολής της ορμής του σώματος είναι ίσο με 4/3.m.υ τότε η μεταβολή της κινητικής ενέργειας ισούται με :
(α) 0 (β) - 4/9 m υ2 (γ) - 16/9 m υ2
Να επιλέξετε τη σωστή απάντηση. μονάδες 2
Να δικαιολογήσετε την επιλογή σας. μονάδες 9
Β2. Tο σώμα Β του σχήματος είναι ακίνητο πάνω σε λείο οριζόντιο δάπεδο και δεμένο στην άκρη ιδανικού ελατηρίου. Το σώμα Α, μάζας mA , κινούμενο με ταχύτητα υΑ=3m/s κατά μήκος του άξονα του ελατηρίου, συγκρούεται κεντρικά με το σώμα Β τη χρονική στιγμή t=0. Οι αλγεβρικές τιμές των ταχυτήτων των σωμάτων μετά την κρούση (θετική φορά προς τα αριστερά) φαίνονται στο διάγραμμα ταχυτήτων-χρόνου.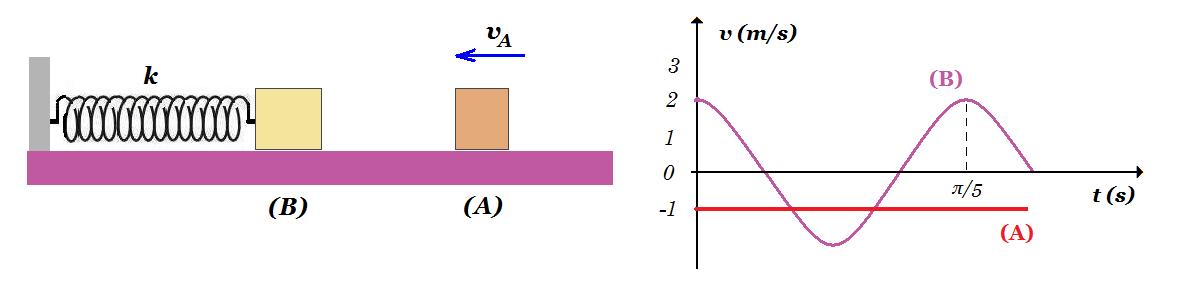
Β2.(Α) Οι μάζες των σωμάτων Α και Β συνδέονται με τη σχέση :
α) mA = mB β) mB = 2mA γ) mΑ = 2mΒ
Να επιλέξετε τη σωστή απάντηση. μονάδες 2
Να δικαιολογήσετε την επιλογή σας. μονάδες 5
Β2.(Β) Η κρούση των σωμάτων είναι :
α) πλαστική β) ελαστική γ) ανελαστική
Να επιλέξετε τη σωστή απάντηση. μονάδες 2
Να δικαιολογήσετε την επιλογή σας. μονάδες 5
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
ΘΈΜΑ Γ.
H εξίσωση που περιγράφει την ένταση του ηλεκτρικού πεδίου σε ένα ηλεκτρομαγνητικό κύμα το οποίο διαδίδεται στο κενό ή στην ατμόσφαιρα της Γης είναι : Ε(x,t) = 300.ημ(2π·1018t - 2π·x/λ) (SI).
α. Να γραφεί η εξίσωση που περιγράφει την ένταση του μαγνητικού πεδίου και να εξεταστεί αν το κύμα αυτό ανήκει στην ορατή περιοχή του φάσματος. μονάδες 4
β. Να σχεδιαστεί το στιγμιότυπο της έντασης του ηλεκτρικού πεδίου του κύματος τη στιγμή t=2·10-18s. μονάδες 4
γ. Το Η/Μ κύμα προσπίπτει κάθετα σε κατακόρυφα τοποθετημένη μεταλλική επιφάνεια στο σημείο Ο και ανακλάται χωρίς απώλεια ενέργειας. Το ανακλώμενο κύμα δημιουργεί με το προσπίπτον, στάσιμο κύμα. Στο σημείο Ο δημιουργείται δεσμός. Πόση είναι η απόσταση μεταξύ του 2ου δεσμού και της 5ης κοιλίας του στασίμου Η/Μ κύματος. μονάδες 3
δ. Ένα φωτόνιο της ηλεκτρομαγνητικής ακτινοβολίας συχνότητας f = 1020 Hz σκεδάζεται από ένα ακίνητο ηλεκτρόνιο. Το σκεδαζόμενο φωτόνιο κινείται κάθετα προς τη διεύθυνση του προσπίπτοντος φωτονίου. Στο χώρο υπάρχει ομογενές μαγνητικό πεδίο εντάσεως Β=0,01Τ. Να υπολογίσετε την εφαπτομένη της γωνίας που σχηματίζει η ταχύτητα του ηλεκτρονίου αμέσως μετά την σκέδαση, με τη διεύθυνση της κίνησης του αρχικού φωτονίου. Μελετήστε την κίνηση του σκεδαζόμενου ηλεκτρονίου μέσα στο μαγνητικό πεδίο εάν η ταχύτητά του αμέσως μετά την σκέδαση σχηματίζει με τις δυναμικές γραμμές του πεδίου γωνία 45°. μονάδες 7
ε. Φωτίζουμε την κάθοδο στο φωτοηλεκτρικό φαινόμενο που είναι η επιφάνεια ενός μετάλλου, με "πράσινο φως" λ = 500 nm, ενώ υπάρχει διαφορά δυναμικού V = +1 V. Υπολογίστε την κινητική ενέργεια ενός ηλεκτρονίου που εξέρχεται από την επιφάνεια του μετάλλου όταν φθάνει στην άνοδο. Το έργο εξαγωγής του μετάλλου είναι 2,4 eV. Πόση είναι η τάση αποκοπής των ηλεκτρονίων της καθόδου; Αν το έργο εξαγωγής του μετάλλου είναι 6,25 eV (λευκόχρυσος) πόση πρέπει να είναι η τάση για να φθάσουν τα ηλεκτρόνια με την μέγιστη ταχύτητα στην άνοδο; μονάδες 7
h = 6,6 10-34 J.s h / mc = 2,4 pm c = 3 108 m/s 1 eV = 1,6 10-19 J λ' - λ = h / mc (1 - συνφ)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
ΘΈΜΑ Δ.
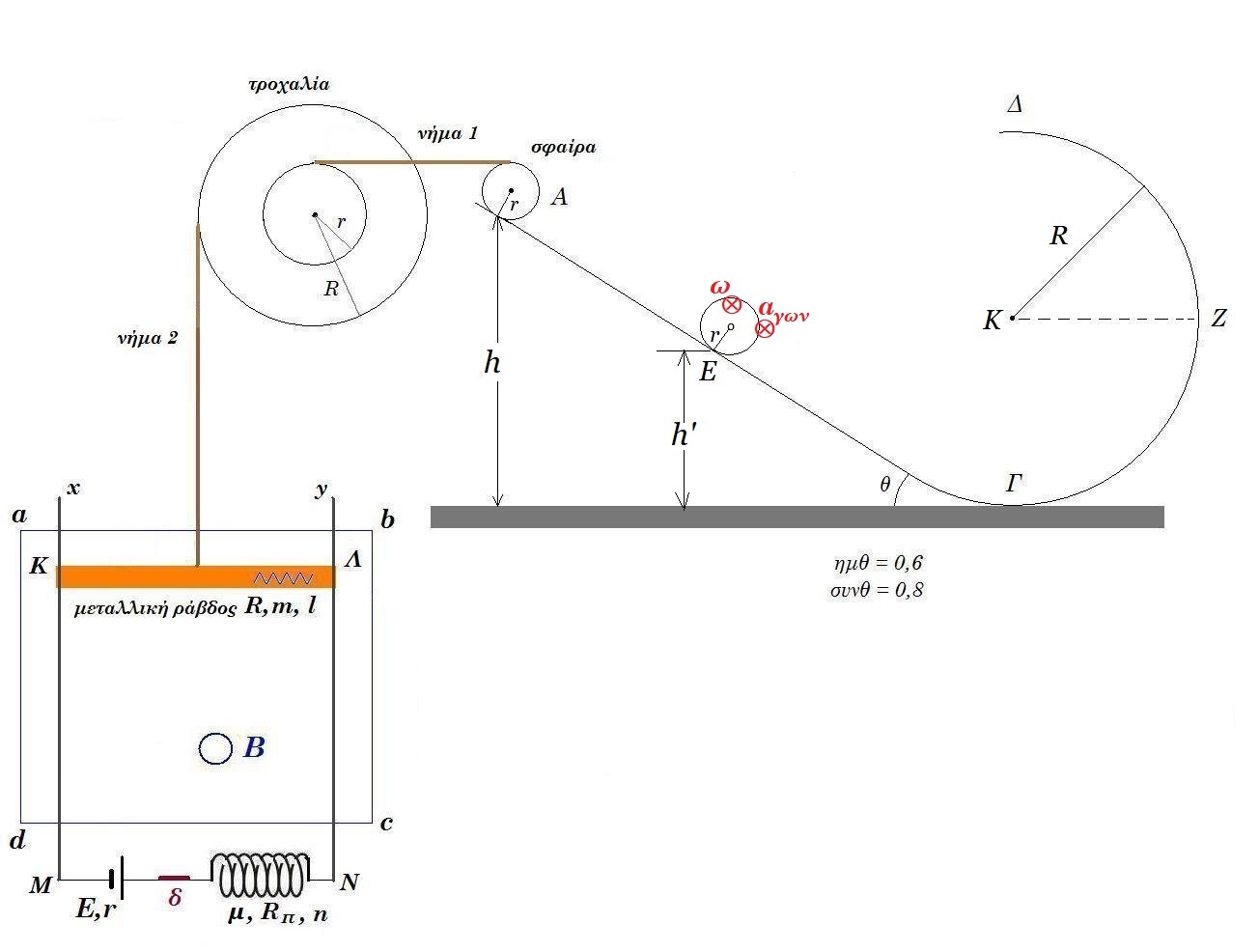
Θεωρούμε την διάταξη του σχήματος, σε κατάσταση ισορροπίας, σε κατακόρυφο επίπεδο. Στη θέση Α του κεκλιμένου επιπέδου ισορροπεί ομογενής σφαίρα μάζας m = 3kg , ακτίνας r = 0,1m. Το κεκλιμένο επίπεδο γωνίας κλίσεως θ, ( ημθ = 0,6 συνθ = 0,8 ) στην βάση του συνδέεται με κατακόρυφο ημικύκλιο ακτίνας R = 1m. Η σφαίρα στο άνω της άκρο συνδέεται με οριζόντιο αβαρές μη εκτατό νήμα 1 (σταθερού μήκους) με τροχαλία μάζας Μ = 5kg εσωτερικής ακτίνας rτροχ = 0,2m , εξωτερικής ακτίνας Rτροχ = 0,5m. Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από άξονα που διέρχεται από το κέντρο της και είναι κάθετος στο επίπεδο της. Γύρω από την τροχαλία έχουμε τυλίξει αρκετές φορές αβαρές μη εκτατό νήμα 2 το οποίο συνδέεται με την μεταλλική ράβδο ΚΛ στο μέσον αυτής. Η μεταλλική ράβδος ισορροπεί σε οριζόντια θέση, έχει μήκος l = 1m και μάζα m=0,5kg, είναι σε επαφή με κατακόρυφους αγωγούς Mx, Ny. Το πηνίο φέρει 1000 σπείρες/m, διαρρέεται από συνεχές ρεύμα εντάσεως Ι, ενώ στο κέντρο του το μέτρο της εντάσεως του μαγνητικού πεδίου είναι Βπην = 4π 10-3 Tesla. Στον χώρο abcd υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο εντάσεως Β.
Δ1. Βρείτε την ένταση του μαγνητικού πεδίου Β φορά, μέτρο. μονάδες 8
Κάποια στιγμή ( t = 0 ) αφαιρούμε το νήμα 1 και ταυτόχρονα ανοίγουμε τον διακόπτη δ, οπότε η σφαίρα κατέρχεται επί του κεκλιμένου επιπέδου κυλιόμενη ( μη ολισθαίνουσα ) ενώ η ράβδος κινείται κατακόρυφα προς τα κάτω ενώ είναι συνεχώς σε επαφή με τους αγωγούς Mx, Ny και η τροχαλία περιστρέφεται γύρω από τον άξονά της χωρίς τριβές έχοντας γωνιακή επιτάχυνση αγων = 10/3 rad/s2 .
Δ2. Εξηγείστε γιατί φορτίζεται η κατερχόμενη ράβδος ΚΛ. Εκφράστε την τάση VΛΚ στα άκρα της, συναρτήσει του χρόνου εάν η ένταση του μαγνητικού πεδίου έχει μέτρο Β = 0,1 Τesla. μονάδες 5
Η σφαιρα κυλίεται ( δεν ολισθαίνει ) κινούμενη στο κεκλιμένο επίπεδο, διέρχεται από την θέση Γ, ανέρχεται κυλιόμενη στο ημικύκλιο και διέρχεται από την ανώτατη Δ του ημικυκλίου έχοντας ταχύτητα μέτρου υ = 3m/s.
Δ3. Η σφαίρα κυλιόμενη επί του κεκλιμένου επιπέδου έχει γωνιακή επιτάχυνση αγων = 300/7 rad/s2. Βρείτε την ταχύτητα του ανώτερου σημείου της σφαίρας τη χρονική στιγμή t = 1s που βρίσκεται στο σημείο Ε σε ύψος h'. μονάδες 7
Δ4. Όταν η σφαίρα διέρχεται από την θέση Δ βρείτε την δύναμη που δέχεται από το ημικύκλιο καθώς και την γωνιακή ταχύτητάς της ( διεύθυνση, φορά, μέτρο ) μετά από 0,2 sec. μονάδες 5
Δίνονται : μαγνητική διαπερατότητα του κενού μο = 4π 10-7 Ν/Α2 , επιτάχυνση βαρύτητας g = 10 m/s2
.............................................................................................................................................................