γραπτές εξετάσεις απαντήσεις στα θέματα 16 / 5 / 2023

https://www.youtube.com/watch?v=29yMwB0HrQ4

E - L di/dt = i 3 r => - L di/dt = 3r (i - E/3r) => di / (i - E/3r) = - 3r/L dt =>

=> ln { (i - E/3r)/(- E/3r) = - 3r/L t => i(t) = E/3r ( 1 - e^{-3r/L t} )

di/dt = E/L e^{-3r/L t}

P_E = E i = E E/3r ( 1 - e^{-3r/L t} ) => P_E = E²/3r ( 1 - e^{-3r/L t} )

P_R+r = i² (R+r) = (E/3r)² ( 1 - e^{-3r/L t} )² 3r => P_R+r = E²/3r ( 1 - e^{-3r/L t} )²

dU_L/dt = L i di/dt = L E/3r ( 1 - e^{-3r/L t} ) E/L e^{-3r/L t} => dU_L/dt = E²/3r ( 1 - e^{-3r/L t} ) e^{-3r/L t}

i = dq/dt => dq = i dt = E/3r ( 1 - e^{-3r/L t} ) dt => q(t) = E/3r t + E/3r L/3r ( e^{-3r/L t} - 1 ) =>

=> q(t) = E/3r L/3r ln(k+1) + E/3r L/3r ( 1/(k+1) - 1 ) =>

=> q(t) = EL/9r² ln(k+1) + EL/9r² k/(k+1) => q = EL/9r² { ln(k+1) + k/(k+1) }

P_E = E²/3r ( 1 - e^{-3r/L t} )

W_E(t) = E²/3r { t + L/3r ( e^{-3r/L t} - 1 ) }

W_E = E²/3r { 5L/3r + L/3r ( - 1 ) } = 4LE²/9r² (1)

P_R+r = E²/3r ( 1 - e^{-3r/L t} )² = E²/3r ( 1 - 2 e^{-3r/L t} + e^{-6r/L t} ) =>

Q_R+r(t) = E²/3r { t + 2L/3r ( e^{-3r/L t} - 1 ) - L/6r ( e^{-6r/L t} - 1 ) }

Q_R+r = E²/3r ( 5L/3r - 2L/3r + L/6r ) = E²/3r 7L/6r = 7L E²/18r² (2)

dU_L/dt = E²/3r ( 1 - e^{-3r/L t} ) e^{-3r/L t} = E²/3r ( e^{-3r/L t} - e^{-6r/L t} )

U_L(t) = E²/3r { - L/3r ( e^{-3r/L t} - 1 ) + L/6r ( e^{-6r/L t} - 1 ) }

U_L = E²/3r ( + L/3r - L/6r ) = E²L/18r² (3)

Q_R+r / U_L = k => 7L E²/18r² = k E²L/18r² => k = 7

i = dq/dt => dq = i dt = E/3r ( 1 - e^{-3r/L t} ) dt => q(t) = E/3r t + E/3r L/3r ( e^{-3r/L t} - 1 ) =>

=> q(t) = E/3r 5L/3r + E/3r L/3r ( - 1 ) =>

=> q(t) = 5EL/9r² - EL/9r² => q = 4EL/9r²

A1. (δ) Β_κυκλ. = 10^-7 2π i/R Biot - Savart dB = 10^-7 i dl/R² ημ90°

B_(O) = ΣdB = 10^-7 i Σdl/R² ημ90° = 10^-7 i R φ /R² = 10^-7 i φ/R

Α2. (α) (iv) (β) (iii)

Α3. (γ) Τ = 8s ω = 2π/8 = π/4 rad/s υ(t) = 10π ημ(π/4^.t) x(t) = - 40 συν(π/4^.t) = 40 ημ(π/4^.t + 3π/2)

Α4. (δ)

G M₁ M₂ / (r₁ + r₂)² = M₁ v₁² / r₁ = M₂ v₂² r₂ => M₁ ω² r₁ = M₂ ω² r₂ => M₁ r₁ = M₂ r₂ => M₁ r₁ = ½ M₁ r₂ => r₁ = ½ r₂ => 2 r₁ = r₂

ο κυανούς Β έχει υψηλότερη θερμοκρασία στην επιφάνειά του σε σχέση με τον ερυθρό αστέρα Α

διότι λ ^. Τ = σταθερά

L₁ = M₁ v₁ r₁ = M₁ ω r₁² L₂ = M₂ v₂ r₂ = M₂ ω r₂² = ½ M₁ ω 4 r₁² = 2 L₁

Μ₁ > Μ₂ => r₁ < r₂ => L₁ < L₂

Α5. (α) Λ P_μέση = i_εν² R => 10 Watt = i_εν² 10 Ω => i_εν² = 1 => i_εν = 1 Α => i₀ = 2^½ Α => i(t) = 2^½ημ(5πt) , (β) Σ , (γ) Λ , (δ) Σ , (ε) Λ

Β1. Δp = p_τελ - p_αρχ => Δp = - m.v' - m.v => - 4/3 m v = - m.v' - m.v => - 1/3 v = v'

Β2. (Α) (β) διατήρηση ορμής m_A 3m/s = m_A (-1m/s) + m_B 2m/s => 2m_A = m_B ,

(Β) (β) K_αρχ = ½ m_A (3m/s)² = 9/2 m_A , Κ_τελ = ½ m_A (-1m/s)² + ½ m_Β (2m/s)² = ½ m_A + ½ 2m_Α 4 = 9/2 m_A άρα Κ_αρχ = Κ_τελ ελαστική κρούση

(α) εξίσωση έντασης του ηλεκτρικού πεδίου Ε(x,t) = E₀ ημ 2π(ft - x/λ) = 300· ημ 2π(10¹⁸ t - x/λ ) (S.I.)

f = 10¹⁸ Hz c = λ f => λ = c / f = 3·10⁸m/s / 10¹⁸ Hz => λ = 3·10^-10m = 0,3 nm < 400 nm (ιώδες) aκτίνες Χ

εξίσωση της έντασης του μαγνητικού πεδίου Β(x,t) = B₀ ημ 2π( ft - x/λ ) = 10^-6· ημ 2π(10¹⁸ t - 10¹⁰ x/3 ) (S.I.)

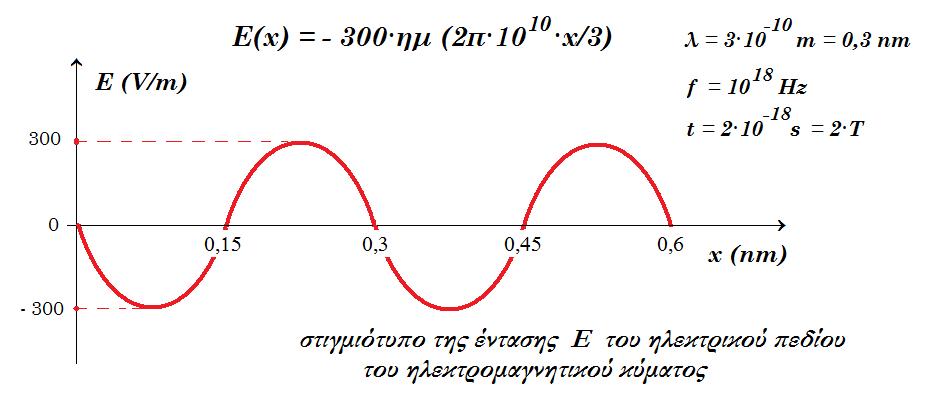
(β) t=2·10^-18s Ε(x) = 300·ημ 2π(10¹⁸·2·10^-18 - 10¹⁰ x/3 ) = 300·ημ (4π - 2π·10¹⁰·x/3) =>

(γ) προσπίπτον Η/Μ κύμα : Β(x,t) = B₀ ημ 2π( ft - x/λ ) = 10^-6·ημ 2π(10¹⁸ t - 10¹⁰ x/3 ) (S.I.)

ανακλώμενο Η/Μ κύμα : Β'(x,t) = B₀ ημ (2πft + 2πx/λ + π) = 10^-6·ημ (2π 10¹⁸ t + 2π 10¹⁰ x/3 + π) (S.I.)

στάσιμο Η/Μ κύμα : Β"(x,t) = 2 B₀ συν (2πx/λ + π/2) ημ (2πft + π/2) = - 2B₀ ημ(2πx/λ) συν(2πft)

Β(x,t) + Β'(x,t) = B₀ ημ (2πft - 2πx/λ) + B₀ ημ (2πft + 2πx/λ + π) =

= 2B₀ ημ ( 2πft - 2πx/λ + 2πft + 2πx/λ + π ) / 2 συν ( 2πft - 2πx/λ - 2πft - 2πx/λ - π ) / 2 =

= 2B₀ ημ ( 4πft + π ) / 2 συν ( - 4πx/λ - π ) / 2 = 2B₀ ημ ( 2πft + π/2 ) συν ( - 2πx/λ - π/2 ) =

= 2B₀ [ συν(2πx/λ) συν(π/2) - ημ(2πx/λ) ημ(π/2) ] [ ημ(2πft) συν(π/2)+ συν(2πft) ημ(π/2) ] =

= 2B₀ [ - ημ (2πx/λ) ] [ + συν (2πft) ] = - 2B₀ ημ(2πx/λ) συν(2πft)

(δ) E = h f = 6,6 10^-34 J.s 10²⁰ Hz = 6,6 10^-14 J ενέργεια προσπίπτοντος φωτονίου

=> λ' - 3 10^-12 m = 6,6 10^-34 / ( 9 10^-31 3 10⁸ ) ( 1 - 0 ) = 0,24 10^-11 m => λ' - 3 10^-12 m = 2,4 10^-12 m =>

f ' = c / λ' = 3 10⁸ / 5,4 10^-12 = 0,55 10²⁰ Hz συχνότητα σκεδαζομένου φωτονίου

ενέργεια σκεδαζομένου φωτονίου : E' = h f ' = 6,6 10^-34 J.s 0,55 10²⁰ Hz = 3,63 10^-14 J = 2,27^.10³ eV

διατήρηση ορμής : p_e,x = E/c => p_e συνθ = h / λ (1) p_e,y = E'/c => p_e ημθ = h / λ' (2)

(ε) h f + eV = K_e + φ => 6,6 10^-34 6 10¹⁴ + 1,6 10^-19 1 = K_e + 2,4 ^. 1,6 10^-19 =>

=> 39,6 10^-20 + 1,6 10^-19 = K_e + 3,84 10^-19 => 0,12 10^-19 + 1,6 10^-19 = K_e = 1,72 ^.10^-19 J

h f + eV = K_e + φ => h f + e V₀ = φ => 6,6 10^-34 6 10¹⁴ + 1,6 10^-19 V₀ = 2,4 1,6 10^-19 =>

=> 3,96 10^-19 + 1,6 10^-19 V₀ = 3,84 10^-19 => - 0,12 10^-19 / 1,6 10^-19 = V₀ = - 0,12 / 1,6 V = - 0,075 V

f = c / λ = 3 10⁸ / 5 10^-7 = 0,6 10¹⁵ Hz = 6 10¹⁴ Hz V = φ/e - h/e f f₀ = φ/e

ροπές ως προς το κέντρο της σφαίρας : Στ = 0 => Τ₂ r = Τ_τρ r => Τ₂ = Τ_τρ

οριζόντιος άξονας : Τ₂ + Τ_τρ συνθ = Ν ημθ => Τ₂ + Τ₂ 0,8 = Ν 0,6 => 1,8 Τ₂ = 0,6 Ν => Ν = 3 Τ₂

κατακόρυφος άξονας : Τ_τρ ημθ + Ν συνθ = mg => Τ₂ 0,6 + 3 Τ₂ 0,8 = 30 => 3Τ₂ = 30 => Τ₂ = 10Ν

ισορροπία τροχαλίας : ροπές ως προς το κέντρο : Στ = 0 => Τ₂ r_τροχ. = Τ₁ R_τροχ. =>

ισορροπία ράβδου : ΣF_y = 0 => T₁ + F_L = mg => 4N + F_L = 0,5 10 => F_L = 1 Newton κατακόρυφη με φορά προς τα πάνω

F_L = B i l => 1Ν = B 10Α 1m => B = 0,1 Tesla με φορά προς τα έξω

Δ2. η ράβδος κατέρχεται με επιτάχυνση α = α_γων R = 10/3 rad/s² 0,5 m = 5/3 m/s²

Ε_επαγ = Β l v = 0,1 T 1 m 5/3 t = t/6 = V_ΚΛ Κ (+) Λ(-) V_ΛΚ = - t/6

Δ3. α_γων = 300/7 rad/s² ω = α_γων t = 300/7 rad/s² 1 s = 300/7 rad/s

υ² = υ_cm² + (ω r)² + 2 υ_cm ω r συνθ = 2 υ_cm² ( 1 + συνθ ) = 2 (30/7)² (1 + 0,8 ) =

Δ4. όταν η σφαίρα διέρχεται από την ανώτερη θέση Δ με υ_Δ = 3 m/s :

ΣF_y = F_κ => mg + Ν = m v_Δ² / (R - r) => 30Ν + Ν = 3kg (3m/s)² / (1m - 0,1m) =>

άρα μόλις η σφαίρα διέρχεται από την ανώτερη θέση Δ του ημικυκλίου Ν = 0

η σφαίρα στον αέρα δεν δέχεται δύναμη που να δημιουργεί ροπή συνεπώς η γωνιακή ταχύτητά της είναι σταθερή : ω = υ_Δ / r = 3 m/s / 0,1 m = 30 rad/s

Δ2. θα μελετήσουμε την κίνηση της ράβδου και την περιστροφή της τροχαλίας

διακόπτης δ κλειστός : Ε - L di/dt + B v l = i ( R_ΚΛ + r + R_πην ) (1)

αρχικά Ι₀ = Ε / ( R_ΚΛ + r + R_πην ) => Ι₀ = Ε / R_ολική = 10 Α

η ράβδος ΚΛ κατέρχεται με επιτάχυνση α η τροχαλία περιστρέφεται με γωνιακή επιτάχυνση : α_γων = α/R

περιστροφή τροχαλίας ως προς το κέντρο της : Στ = Ι_τροχ. α_γων => R Τ₁ = ½ Μ R² α_γων =>

=> Τ₁ = ½ Μ R α_γων = ½ Μ α (3) τάση νήματος από την διπλή τροχαλία μάζας Μ

(2) , (3) => mg - Bil = ma + ½ Μ α => mg - Bil = (m + ½Μ) α => i = [mg - (m + ½Μ) α]/Bl (4)

αρχικά υ(0) = 0 i(0) = I₀ = Ε/R_ολική οπότε mg - Bil = (m + ½Μ) α =>

α(0) = ( mg - BlΕ/R_ολική ) / (m + ½Μ) = ( 0,5 10 - 0,1 1 10 ) / ( 0,5 + 2,5 ) = 4/3 m/s²

=> Ε + L (m + ½Μ) / Bl da/dt + Bl v = R_ολική [ mg - (m + ½Μ) α ] / Bl =>

=> Ε + L (m + ½Μ) / Bl d²υ/dt² + Bl v = R_ολική [ mg - (m + ½Μ) dυ/dt ] / Bl =>

=> L(m + ½Μ)/Bl d²υ/dt² - R_ολικήmg/Bl + R_ολική(m + ½Μ)/Bl dυ/dt + Bl v + Ε = 0 =>

=> L(m + ½Μ)/Bl d²υ/dt² + R_ολική(m + ½Μ)/Bl dυ/dt + Bl v + Ε - R_ολικήmg/Bl = 0

θέτουμε : Α₁ = L (m + ½Μ) / Bl και Α₂ = R_ολική (m + ½Μ) / Bl

οπότε έχουμε : Α₁ d²υ/dt² + Α₂ dυ/dt + Bl v + Ε - R_ολικήmg/Bl = 0 (6)

παραγωγίζοντας την (6) έχουμε Α₁ v''' + Α₂ v'' + Bl v' = 0

το χαρακτηριστικό πολυώνυμο : Α₁ ρ³ + Α₂ ρ² + Bl ρ = 0 => ρ ( Α₁ ρ² + Α₂ ρ + Bl ) = 0

Δ = Α₂² - 4 Α₁ Bl = R²_ολική (m + ½Μ)² / B²l² - 4 L (m + ½Μ)

οι λύσεις ρ₁ = ( - Α₂ + √Δ ) / 2Α₁ ρ₂ = ( - Α₂ - √Δ ) / 2Α₁ ρ₃ = 0

εάν ρ = 0 σημαίνει ότι υ' = 0 => dv/dt = 0 η επιτάχυνση της ράβδου είναι μηδέν αλλά βρήκαμε ότι η αρχική επιτάχυνση είναι ( mg - BlΕ/R_ολική ) / (m + ½Μ) = 4/3 m/s²

v(t) = G ( e^ρ₁t - e^ρ₂^t ) = G ( e^{( - Α₂ + √Δ ) / 2Α₁ t} - e^{( - Α₂ - √Δ ) / 2Α₁ t} ) =>

=> v(t) = G e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} - e ^{- √Δ ) / 2Α₁ t} )

a = dv/dt = - Α₂/2Α₁ G e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} - e ^{- √Δ ) / 2Α₁ t} ) +

+ G (√Δ /2Α₁) e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} + e ^{- √Δ ) / 2Α₁ t} ) (7)

η (7) => - Α₂/2Α₁ G 1 ( 1 - 1 ) + G (√Δ /2Α₁) 1 ( 1 + 1 ) = ( mg - BlΕ/R_ολική ) / (m + ½Μ) =>

G = A₁( mg - BlΕ/R_ολική ) / (m + ½Μ)√Δ = L( mg - BlΕ/R_ολική ) / Bl√Δ

α(t) = - Α₂/2Α₁ A₁( mg - BlΕ/R_ολική ) / (m + ½Μ)√Δ e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} - e ^{- √Δ ) / 2Α₁ t} ) +

+ A₁( mg - BlΕ/R_ολική ) / (m + ½Μ)√Δ (√Δ /2Α₁) e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} + e ^{- √Δ ) / 2Α₁ t} )

τελικά : v(t) = A₁( mg - BlΕ/R_ολική ) / (m + ½Μ)√Δ e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} - e ^{- √Δ ) / 2Α₁ t} )

α(t) = - ( mg - BlΕ/R_ολική ) Α₂ / 2(m + ½Μ)√Δ e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} - e ^{- √Δ ) / 2Α₁ t} ) +

+ ( mg - BlΕ/R_ολική ) / 2(m + ½Μ) e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} + e ^{- √Δ ) / 2Α₁ t} )

i = mg/Bl + (m + ½Μ)/Bl ( mg - BlΕ/R_ολική )Α₂ / 2√ΔBl e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} - e ^{- √Δ ) / 2Α₁ t} ) +

- (m + ½Μ)/Bl ( mg - BlΕ/R_ολική ) / 2Bl e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} + e ^{- √Δ ) / 2Α₁ t} ) =>

i(t) = mg/Bl + (m + ½Μ)( mg - BlΕ/R_ολική )Α₂ / 2√ΔB²l² e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} - e ^{- √Δ ) / 2Α₁ t} ) +

- (m + ½Μ) ( mg - BlΕ/R_ολική ) / 2B²l² e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} + e ^{- √Δ ) / 2Α₁ t} ) =>

παραγωγίζουμε την σχέση (1) => - L d²i/dt² + Bl dv/dt = ( R_ΚΛ + r + R_πην ) di/dt (8)

mg - Bil = (m + ½Μ) α => mg - Bil = (m + ½Μ) dv/dt => dv/dt = ( mg - Bil ) / (m + ½Μ) (9)

(8) , (7) => - L d²i/dt² + Bl ( mg - Bil ) / (m + ½Μ) = ( R_ΚΛ + r + R_πην ) di/dt =>

=> L d²i/dt² + R_ολική di/dt + B²l²/(m + ½Μ) i - Blmg / (m + ½Μ) = 0 (10)

το χαρακτηριστικό πολυώνυμο : L λ² + R_ολική λ + B²l²/(m + ½Μ) = 0

Δ = R_ολική² - 4 L B²l²/(m + ½Μ) = R_ολική² ( 1 - 4LB²l²/ (m + ½Μ)R_ολική² )

√Δ = R_ολική √( 1 - 4LB²l²/ (m + ½Μ)R_ολική² ) = R_ολική √( 1 - N )

λ₁ = (- R_ολική + √Δ) / 2L = (- R_ολική + R_ολική √( 1 - N ) ) / 2L = R_ολική/ 2L [ -1 + √( 1 - N ) ]

λ₂ = (- R_ολική - √Δ) / 2L = (- R_ολική - R_ολική √( 1 - N ) ) / 2L = R_ολική/ 2L [ -1 - √( 1 - N ) ]

i(t) = I₁ e^λ₁t + I₂ e^λ₂^t = I₁ e^{R_ολική/ 2L [ -1 + √( 1 - N ) ] t} + I₂ e^{R_ολική/ 2L [ -1 - √( 1 - N ) ] t}

αρχικά i = I₀ = E/R_ολική = 10 A i(0) = I₁ + I₂ = E/R_ολική => I₂ = E/R_ολική - I₁

i(t) = I₁ e^{R_ολική/ 2L [ -1 + √( 1 - N ) ] t} + ( E/R_ολική - I₁ ) e^{R_ολική/ 2L [ -1 - √( 1 - N ) ] t}

di/dt = I₁ R_ολική/ 2L [ -1 + √( 1 - N ) ] e^{R_ολική/ 2L [ -1 + √( 1 - N ) ] t} +

+ R_ολική/ 2L [ -1 - √( 1 - N ) ] ( E/R_ολική - I₁ ) e^{R_ολική/ 2L [ -1 - √( 1 - N ) ] t}

Ε - I₁ R_ολική/ 2 [ -1 + √( 1 - N ) ] e^{R_ολική/ 2L [ -1 + √( 1 - N ) ] t} + R_ολική/ 2 [ -1 - √( 1 - N ) ] ( E/R_ολική - I₁ ) e^{R_ολική/ 2L [ -1 - √( 1 - N ) ] t} + Bl v =

= R_ολική I₁ e^{R_ολική/ 2L [ -1 + √( 1 - N ) ] t} + R_ολική ( E/R_ολική - I₁ ) e^{R_ολική/ 2L [ -1 - √( 1 - N ) ] t}

v(t) = I₁ R_ολική/2Bl { 1 + √(1 - N) } e^{R_ολική/ 2L [ -1 + √( 1 - N ) ] t} +

+ ( E/2Bl - I₁ R_ολική/2Bl ) { 3 + √(1 - N) } e^{R_ολική/ 2L [ -1 - √( 1 - N ) ] t} - Ε/Bl

v(0) = 0 => I₁ R_ολική/2Bl { 1 + √(1 - N) } + ( E/2Bl - I₁ R_ολική/2Bl ) { 3 + √(1 - N) } - Ε/Bl = 0

=> I₁ R_ολική/2Bl { 1 + √(1 - N) } + {3 + √(1 - N)} E/2Bl - I₁ { 3 + √(1 - N) } R_ολική/2Bl - Ε/Bl = 0

v(t) = E/4Bl { 1 + √(1 - N) }² e^{R_ολική/ 2L [ -1 + √( 1 - N ) ] t} +

+ E/4Bl ( 1 - √(1 - N) ) { 3 + √(1 - N) } e^{R_ολική/ 2L [ -1 - √( 1 - N ) ] t} - Ε/Bl

v(t) = E/4Bl { 1 + √(1 - N) }² e^{R_ολική/ 2L [ -1 + √( 1 - N ) ] t} +

+ E/4Bl ( 2 + N - 2√(1 - N) ) e^{R_ολική/ 2L [ -1 - √( 1 - N ) ] t} - Ε/Bl

v(t) = A₁( mg - BlΕ/R_ολική ) / (m + ½Μ)√Δ e^{- Α₂ / 2Α₁ t} ( e^{√Δ / 2Α₁ t} - e ^{- √Δ ) / 2Α₁ t} )