Ο αγωγός ΟΑΓ του σχήματος αποτελείται από δύο ράβδους ΟΑ και ΑΓ κάθετες μεταξύ τους με μήκη (ΟΑ) = 0,6 m και (ΑΓ) = 0,8 m. O αγωγός στρέφεται στο επίπεδο της σελίδας γύρω από το άκρο του Ο με σταθερή γωνιακή ταχύτητα μέτρου ω = 10 rad/s κάθετα στις γραμμές ομογενούς μαγνητικού πεδίου μέτρου έντασης Β = 1Τ. Η απόλυτη Η.Ε.Δ. από επαγωγή στα άκρα του αγωγού ΑΓ είναι ίση με:

α. μηδέν                          β. 3,2 V                                   γ. 5 V

   τα ηλεκτρόνια της ράβδου ΟΑ δέχονται δύναμη Lorentz  οπότε κινούνται προς το άκρο Α που φορτίζεται αρνητικά  ενώ το άκρο Ο φορτίζεται θετικά

   τα ηλεκτρόνια της ράβδου ΑΓ δέχονται δύναμη Lorentz  οπότε κινούνται προς το άκρο Γ που φορτίζεται αρνητικά  ενώ το άκρο Α φορτίζεται θετικά

V_ΟΓ = V_OA + V_ΑΓ  =>  B π(ΟΓ)² / Τ  =  Β π(ΟΑ)² / Τ  + V_ΑΓ =>  Β ω/2 (ΟΓ)²  =  Β ω/2 (ΟΑ)²  + V_ΑΓ  =>

  => V_ΑΓ  =  1Τ  10 rad/s / 2  1m²  -  1T  10 rad/s / 2  0,36m²  =  3,2 V 

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

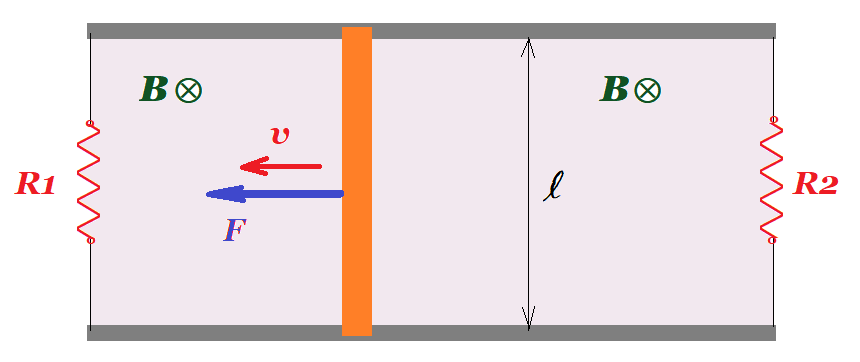
Συρμάτινο κυκλικό πλαίσιο, το οποίο αποτελείται από 10 σπείρες, με εμβαδόν κάθε σπείρας Α=0,01m², βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο με το επίπεδό του σε οριζόντιο επίπεδο, κάθετο στις δυναμικές γραμμές ενός κατακόρυφου ομογενούς μαγνητικού πεδίου έντασης Β₀=1Τ. Κάποια στιγμή το μαγνητικό πεδίο αρχίζει να αυξάνεται με σταθερό ρυθμό και γίνεται Β₁=2Τ σε χρόνο Δt=2s. Το πλαίσιο παρουσιάζει αντίσταση r=2Ω, ενώ τα δυο άκρα του σύρματος συνδέονται με μια αντίσταση R=3Ω.

i)  Να υπολογίσετε την ένταση του ρεύματος που διαρρέει το κύκλωμα. Ποια είναι η φορά της έντασης;

ii)  Να υπολογισθεί η ενέργεια του μαγνητικού πεδίου που μετατρέπεται σε ηλεκτρική ενέργεια στο κύκλωμα, στο παραπάνω χρονικό διάστημα.

iii) Να υπολογιστεί το φορτίο που πέρασε από τον αντιστάτη R, στο παραπάνω χρονικό διάστημα.

iv) Σε μια επανάληψη του πειράματος, μεταβάλλουμε κατάλληλα το μαγνητικό πεδίο, ξεκινώντας ξανά από την τιμή Β₀, οπότε ο αντιστάτης R διαρρέεται από ρεύμα, με φορά από το Α στο Γ, με μεταβλητή ένταση όπως στο διάγραμμα.

     α) Να υπολογιστεί ο ρυθμός μεταβολής της έντασης του μαγνητικού πεδίου τις χρονικές στιγμές t₀⁺ και t₂=1s.

     β) Ποια η ένταση του μαγνητικού πεδίου τη στιγμή t₂;

    B(t) = 0,5.t + 1 (Tesla)

Ε_επαγ = - ΔΦ/Δt = - A ΔΒ/Δt N = - 0,01m²  (2T - 1T)/2s  10 σπείρες  = - 0,05 V   =  i (r + R)  = i (2 + 3)  =>  i = - 0,01 A  όπως κινούνται οι δείκτες του ρολογιού     Β_επαγ κατακόρυφο προς τα κάτω

Q_θερμ = i² (r + R) t = 0,01²  5  2  = 0,001 J                  q = i t = 0,01 A  2 s = 0,02 Coulomb  

i(t) = (12 - 4t) mA        Ε_επαγ = i (r + R)  = (12 - 4t) 5  = (60 - 20t) mV     

Ε_επαγ = - ΔΦ/Δt = - A ΔΒ/Δt N =>  (60 - 20t) mV  = - A ΔΒ/Δt N  =>  (60 - 20t) mV  = - 0,01  ΔΒ/Δt  10  =>  (60 - 20t) mV  = - 0,1 ΔΒ/Δt   => - (600 - 200t) mT  = ΔΒ/Δt  =>  ΔΒ/Δt  =  0,2t - 0,6 (T)   

t = 0⁺    ΔΒ/Δt  =  - 0,6 T/s                             t = 1s     ΔΒ/Δt  =  0,2 - 0,6 = - 0,4 T/s     

t = 1s           

dB/dt = 0,2t - 0,6  =>  dB = (0,2t - 0,6)dt  =>  B - B₀ =  0,5 0,2 t² - 0,6 t  =>  B = 1 + 0,1 - 0,6 = 0,5 Tesla 

από το εμβαδόν του τραπεζίου θα βρούμε το φορτίο που διέρχεται από το κύκλωμα σε 1s  

  q = (12 + 8)mA / 2  1s = 10 mC  = 0,01 Coulomb    

 q  =  Ν |ΔΦ|/(r + R) =  Ν Α |ΔΒ|/(r + R)  =  Ν Α |Β - Β₀|/(r + R)  =>

   =>  0,01  =  10  0,01  |Β - 1|/5  =>  Β = 0,5 Τ   διότι μειώνεται η ένταση του μαγνητικού πεδίου  επειδή    για τη στιγμή  t = 1s   είναι  ΔΒ/Δt  =  0,2 - 0,6 = - 0,4 T/s     

Σφαίρα (Σ) μάζας m₁=1kg συγκρατείται σε ύψος h=1,4m, πάνω από μια πλάκα (Π), μάζας m₂=2kg, η οποία ηρεμεί στο πάνω άκρο κατακόρυφου ελατηρίου σταθεράς k=50Ν/m, όπως στο σχήμα. Θέτουμε την πλάκα σε κατακόρυφη ταλάντωση πλάτους Α και στη συνέχεια, κάποια στιγμή (t_ο=0) αφήνουμε ελεύθερη την σφαίρα να πέσει κατακόρυφα και να συγκρουσθεί την στιγμή t₁=0,6s, με την πλάκα. Αν η κρούση μεταξύ των δύο σωμάτων είναι κεντρική και ελαστική και η σφαίρα, μετά την κρούση, αποκτά ταχύτητα προς τα πάνω μέτρου 4m/s, να βρεθούν:

α)  η δυναμική ενέργεια του ελατηρίου την στιγμή της κρούσης.

β)  το πλάτος Α της ταλάντωσης, πριν την κρούση.

γ)  το νέο πλάτος Α' της ταλάντωσης της πλάκας, μετά την κρούση.

Δίνεται g=10m/s².

ισορροπία Σ₂ :    m₂ g = k y₀  =>  20 = 50 y₀  =>  y₀ = 0,4 m    συσπείρωση ελατηρίου 

στην Θ.Ι.  το ελατήριο είναι συσπειρωμένο κατά  y₀ = 0,4 m

α)       h = 0,5 g t² =  0,5 10  0,6²  = 1,8 m              v₁ = g t = 10  0,6 = +6 m/s       θετική προς τα κάτω

τη στιγμή  t = 0,6 s   η απομάκρυνση του Σ₂  είναι  y =  1,8 m  -  1,4 m  =  + 0,4 m   θετική προς τα κάτω

άρα το  ελατήριο είναι συσπειρωμένο κατά   0,4 m + y₀ = 0,8 m     οπότε  έχει δυναμική ενέργεια :

                        U_ελατ = 0,5  50 N/m  (0,8 m)²  =>   U_ελατ = 16 J       

β)     ελαστική κρούση :  

    v₁'  =  v₁ (m₁ - m₂) / (m₁ + m₂)  +  2 m₂ v₂ / (m₁ + m₂)   =>

=>  - 4  =  6 (1 - 2) / 3  +  2 2 v₂ / 3  =>  - 4  = - 2  +  4 v₂ / 3  =>  - 2 =  +  4 v₂ / 3  =>  v₂ = - 3/2 m/s    

   ταλάντωση του Σ₂ :    ω² = k/m₂ = 50 / 2 => ω = 5 rad/s  

  y(t) = A ημ(5t + θ)             v(t) = 5A συν(5t + θ)             α(t) = - 25A ημ(5t + θ) 

    y(0) = A ημθ        v(0) = 5A συνθ       

  y(0,6) = A ημ(5  0,6 + θ) = A ημ(3 + θ)  =  0,4 m   =>   Α ημ(3 + θ)  =  0,4    (1)

  v(0,6) = 5A συνθ = 5A συν(5 0,6 + θ)  = 5A συν(3 + θ)     

   v₂  =  v(0,6)  =>   5A συν(3 + θ)  =  - 3/2   =>  Α συν(3 + θ) =  - 0,3    (2)   

(1)² + (2)²  =>   Α²  =  0,4²  +  0,3²  =  0,5²  =>  Α =  0,5 m

επειδή    ημ3  @  ημπ  = 0     και     συν3  @  συνπ = - 1

έχουμε :   ημ(3 + θ)  =  0,4 / 0,5 = 0,8  =>  ημ3  συνθ  +  συν3  ημθ  =  0,8   =>  ημθ =  - 0,8  

και      συν(3 + θ) =  - 0,3 / 0,5 = - 0,6  =>  συν3  συνθ  -  ημ3  ημθ  =  - 0,6  =>  συνθ = 0,6

γ)     v₂'  =  v₂ (m₂ - m₁) / (m₁ + m₂)  +  2 m₁ v₁ / (m₁ + m₂)   =>  

  =>  v₂'  =  - 3/2  (2 - 1) / 3  +  2 1 6 / 3   =>  v₂'  =  - 1/2   +  4  =>  v₂' = 3,5 m/s   το Σ₂ μετά την κρούση κινείται προς τα κάτω με ταχύτητα 3,5 m/s  και είναι σε απομάκρυνση  0,4 m  από τη Θ.Ι. του  οπότε

διατήρηση ενέργειας για την νέα ταλάντωση :   ½ m₂ (v₂')²  +  ½ k y²  =   ½ k (A')²  => 

   =>   2  3,5²  +  50  0,4²  =  50 (A')²  =>    24,5  +  8  =  50 (A')²  =>    A' = √0,65 m

άλλος τρόπος :

  y(t) = A' ημ(5t + φ)             v(t) = 5A' συν(5t + φθ)             α(t) = - 25A' ημ(5t + φ) 

  y(0) = A' ημφ  =  0,4   (3)         v(0) = 5A' συνφ  = 3,5  =>   A' συνφ  =  0.7   (4)         

 από  (3)² + (4)² =>   (Α')²  =  0,4⁴ + 0,7² = 0,16 + 0,49 = 0,65  =>  A' = √0,65 m      

 από  (3) / (4) =>  εφφ = 4/7   

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

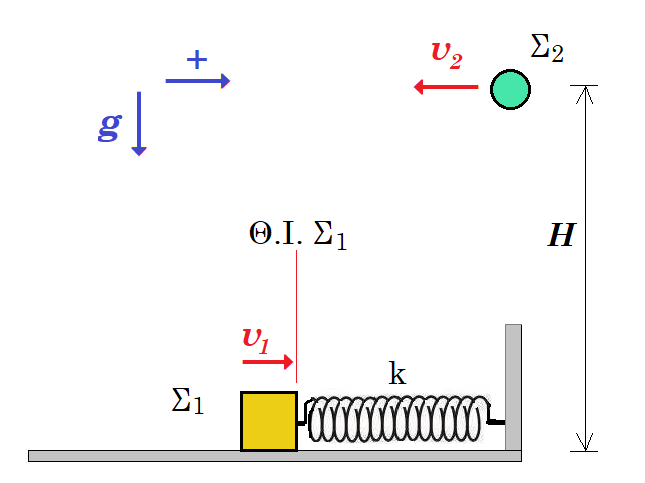
Οριζόντια βολή - ταλάντωση - πλαστική κρούση
Σώμα Σ1 με μάζα m₁ = 1 kg είναι προσδεδεμένο στο αριστερό άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k = 100 N/m και φυσικού μήκους L₀ = 5π/6 - 0,5√3 m, το άλλο άκρο του οποίου είναι προσδεδεμένο σε κατακόρυφο τοίχο μικρού ύψους. Το Σ1 είναι αρχικά ακίνητο πάνω σε λείο οριζόντιο επίπεδο. Την χρονική στιγμή t₀ = 0 από ύψος H = 25/18 m πάνω από το σημείο που είναι προσδεδεμένο το δεξί άκρο του ελατηρίου στον τοίχο βάλλεται σώμα Σ2 μάζας m₂ = 3 kg με οριζόντια ταχύτητα υ₂ = 5 m/s και δέχεται μόνο την δύναμη του βάρους του που την θεωρούμε σταθερή. Την ίδια χρονική στιγμή t₀ το Σ1 ξεκινά να ταλαντώνεται από την θέση ισορροπίας του με θετική ταχύτητα υ₁ ίδιας διεύθυνσης με την διεύθυνση του ελατηρίου και πλάτος ταλάντωσης Α=1m.
Τα σώματα Σ1, Σ2 και το ελατήριο βρίσκονται συνεχώς στο ίδιο κατακόρυφο επίπεδο.
Ως θετική φορά της ταλάντωσης έχει οριστεί η προς τα δεξιά.   Δίνεται g = 10 m/s² και π² ≈ 10.
1)  Να υπολογίσετε τον χρόνο πτώσης του σώματος Σ2.
2)  Να υπολογίσετε την απομάκρυνση του σώματος Σ1 από την θέση ισορροπίας της ταλάντωσης που εκτελεί και την ταχύτητα του την χρονική στιγμή που το Σ2 φτάνει στο έδαφος.
3)  Να ελέγξετε αν τα δυο σώματα συγκρούονται και αν όντως συγκρούονται να θεωρήσετε την κρούση πλαστική και να υπολογίσετε την θερμότητα (Q_κρ) που εκλύεται λόγω της πλαστικής κρούσης των δύο σωμάτων. Θεωρείστε ότι κατα την διάρκεια της κρούσης το συσσωμάτωμα δεν αναπηδά στο οριζόντιο επίπεδο.
4)  Να υπολογίσετε το πλάτος της ταλάντωσης του συσσωματώματος.

1)  οριζόντια βολή Σ₂ :   y = ½ g t²    v_y = g t        v_x = v₂      x = v₂ t   

   y = ½ g t² =  H  =>   ½  10  t² =   25/18  =>  t² = 5/18 = 10/36 = π²/6²  => t = π/6 s  χρόνος πτώσεως του Σ₂   

   v_y = g t = 10  π/6  =>  v_y =  5π/3 m/s     

 ολική ταχύτητα  (v₂')²  =  v_x² + v_y²  =  5² + ( 5π/3 )²  =  5² ( 9 + π² ) / 9   =  5² 19 / 3²  =>  υ₂' = 5/3 √19 m/s

οριζόντια μετατόπιση :    x = v_x t  =  v₂ t  = 5 π/6  = 5π/6 m/s  (1)

2) Α.Α.Τ. του Σ₁ :   ω² = k/m₁ = 100 / 1  => ω = 10 rad/s    x(t) = 1 ημ10t      υ(t) = 10 συν10t      α(t) = - 100 ημ10t 

  x(π/6) = 1 ημ(10 π/6) = ημ(5π/3)  =>   x(π/6) = - 0,5√3 m      

  υ(π/6) = 10 συν(10 π/6) = 10 συν(5π/3) = 10  ½ =>  υ(π/6) = 5 m/s

3)  το μήκος του ελατηρίου εκείνη τη στιγμή είναι   5π/6 - 0,5√3 + 0,5√3   =  5π/6 m   (2)

 από  (1) , (2)  θα γίνει κρούση   

διατήρηση ορμής στον άξονα χ'χ :   m₁ v₁  +  m₂ v_2,x  =  (m₁ + m₂) u  =>  1  5  + 3 (- 5) = 4 u  => u = - 2,5 m/s 

  Κ_1.αρχ  +  Κ_2,αρχ  =  ½ m₁ v₁²  +  ½  m₂ v₂² =    ½ 1  5²  +  ½  3  25 19 / 9 =  91,66 J             

  Κ_τελ =  ½ (m₁ +  m₂) u²  =   ½  4  (- 2,5)² =  12,5 J                            Q = Κ_τελ  - ( Κ_1.αρχ + Κ_2,αρχ ) = - 79,16 J

4)   διατήρηση ενέργειας για την νέα ταλάντωση :   ½ (m₁ +  m₂) u²  +  ½ k x²   =   ½ k (A')²  => 

   =>   4  2,5²  +  100  ( 0,5√3 )²  =  100 (A')²  =>    25  +  75  =  100  (A')²  =>    A' = 1 m

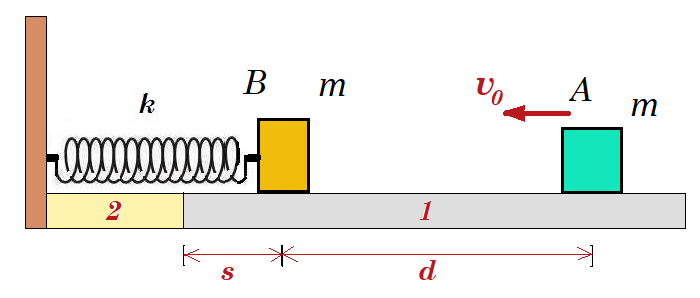
Σε μη λείο οριζόντιο επίπεδο (1) ηρεμούν δύο σώματα Α και Β, ίσης μάζας m=2kg, τα οποία θεωρούμε υλικά σημεία αμελητέων διαστάσεων, απέχοντας κατά d=1,2m, όπου το δεύτερο είναι δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=8Ν/m, το οποίο έχει το φυσικό του μήκος. Σε μια στιγμή εκτοξεύομαι το σώμα Α, με αρχική ταχύτητα υ₀=4m/s, προς το σώμα Β, όπως στο σχήμα. Ο συντελεστής τριβής μεταξύ του σώματος Α και του επιπέδου είναι μ₁=0,5. Μετά από λίγο τα σώματα συγκρούονται κεντρικά και ελαστικά, με αποτέλεσμα το Β να αρχίζει να συμπιέζει το ελατήριο. Μόλις το ελατήριο συμπιεστεί κατά s=0,4m, το σώμα Β, έχοντας ταχύτητα u=0,6m/s, περνά σε ένα δεύτερο λείο οριζόντιο επίπεδο (2), στο οποίο κινείται.              Να βρεθούν:

α)  Οι  ταχύτητες των δύο σωμάτων μετά την μεταξύ τους κρούση.

β)  Η τριβή που δέχεται το Β σώμα από το επίπεδο 1.

γ)  Η μέγιστη επιτάχυνση  του σώματος Β, στη διάρκεια της κίνησής του στο λείο επίπεδο 2.

a = - μ g = - 0,5 10 = - 5 m/s²
1,2 = 4 t - ½ 5 t² => 2,5 t² - 4 t + 1,2 = 0        Δ = 16 - 12 = 4 = 2²
t = (4 + 2)/5 = 1,2 s     ή      t = (4 - 2)/5 = 0,4 s   δεκτή λύση
v = 4 - 5 t = 4 - 5 0,4 = 2 m/s

Τ = μ Ν = μ mg = 0,5  2  10 =  10 N    δύναμη τριβής για το σώμα Α

διατήρηση ενέργειας   ½ m v₀² = ½ m υ² + T d =>    ½ 2 4² = ½ 2 υ² + 10 1,2  =>  υ² = 16 - 12 = 4 => υ = 2 m/s

ίσες μάζες  άρα  ανταλλάσσουν ταχύτητες οπότε το σώμα Β  ακινητοποιείται  και το σώμα Α αποκτά ταχύτητα 2 m/s
διατήρηση ενέργειας   ½ m v²  =  ½ m u²  +  T s  +  ½ k s²  =>    ½ 2 2²  =  ½ 2 0,6²  +  T 0,4  +  ½ 8 0,4²  =>
                              => 4 = 0,36 + T 0,4 + 0,64   => T = 30/4 = 7,5 N
διατήρηση ενέργειας    ½ m v²  =  ½ m 0²  +  T s  +  ½ k χ²  =>
                      =>   ½ 2 2²  -  7,5 0,4  =  0  +  ½ 8 χ²  =>   χ²  =  (4 - 3)/4  =  0,25  =>  χ = 0,5 m
η συνολική συσπείρωση του ελατηρίου είναι 0,5 m ,    0,4 m στην τραχεία επιφάνεια  και  0,1 m  στην λεία επιφάνεια
ω² = 8/2 = 4 => ω = 2 rad/s
ΣF = m a =>  k χ = m a  =>  8 0,5 = 2 a => a = 2 m/s²  μέγιστη επιτάχυνση του σώματος Β  τη στιγμή που το ελατήριο έχει μέγιστη συσπείρωση  και  το σώμα Β  ακινητοποιείται στιγμιαία

  ½ k χ²  =   ½ m v²  +  ½ k (χ - s)²  =>    8 0,5²  =  2 v²  +  8 (0,5 - 0,1)²  =>   1  =   v²  +  0,64  => v = 0,6 m/s

  ½ 8  0,4²  +   ½ 2  0,6²   =  0  +  T s'  + ½ 8  (0,4 - s')²    =>   4  0,16  +   0,36   =   7,5  s'  +  4  (0,4 - s')²    => 

=>   1   =   7,5  s'  +  4  ( 0,16  -  0,8 s'  +  s'² )   =>   1   =   7,5  s'  +  0,64  -  3,2 s'  +  4 s'²    =>

=>     4 s'²  +   4,3  s'  -  0,36  =  0             D =  18,49  +  5,76  =  24,25  =  4,92²       

 (  - 4,3  +  4,92 ) / 8 =  0,078 m                 (  - 4,3  -  4,92 ) / 8 = απορρίπτεται

το σώμα Β  επί της τραχείας επιφανείας κινείται διανύοντας   0,078 m και ακινητοποείται στιγμιαία

το ελατήριο έχει συσπείρωση  0,4 - 0,078 =  0,322 m     και η δύναμη ελατηρίου είναι  k χ = 8  0,322 = 2,576 Ν  <  7,5 Ν  δύναμη τριβής

Στη διάταξη του σχήματος τα ελατήρια είναι ιδανικά με σταθερές k1 = k2 = 100 N/m. Οι μάζες των σωμάτων είναι m1 = m2 = 1 kg. Το Σ1 είναι δεμένο στο ελατήριο σταθεράς k1 και το σώμα Σ2 δεμένο στο ελατήριο σταθεράς k2. Τα σώματα είναι σε επαφή μεταξύ τους. Αρχικά το σύστημα των δύο σωμάτων ισορροπεί ακίνητο με το ελατήριο σταθεράς k1 να έχει το φυσικό του μήκος και το ελατήριο σταθεράς k2 να είναι συσπειρωμένο. Κατεβάζουμε το σύστημα των δύο σωμάτων κατακόρυφα προς τα κάτω κατά d=0,2m και το αφήνουμε ελεύθερο. Δίνεται g = 10 m/s2, οι διαστάσεις των σωμάτων αμελούνται και ότι δεν υπάρχουν αντιστάσεις από τον αέρα. Τα ελατήρια έχουν κοινό κατακόρυφο άξονα. α. Δείξτε ότι το σύστημα των δύο σωμάτων θα εκτελέσει α.α.τ. β. Να βρεθεί η δύναμή του ελατηρίου σταθεράς k2 σε συνάρτηση με την απομάκρυνση γ. Να βρεθεί η μέγιστη δυναμική ενέργεια του ελατηρίου k2 δ. Να βρεθεί η γραφική παράσταση της δύναμης επαφής μεταξύ των σωμάτων σε συνάρτηση με την απομάκρυνση.

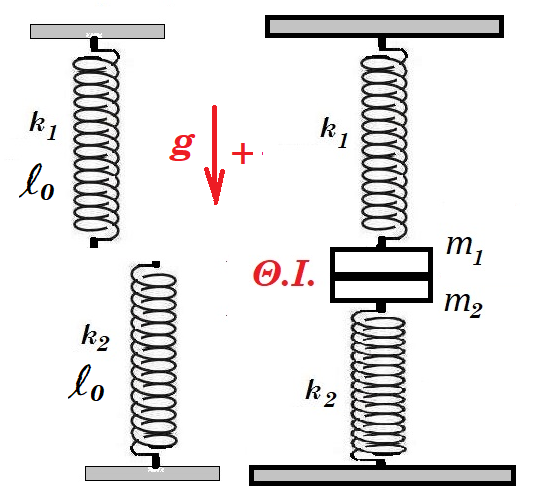ισορροπία σωμάτων :   m₁ g = N₁ =>  N₁ = 10 N  κατακόρυφη προς τα επάνω       

        m₂ g + N₂ =  k₂ x_0,2   =>   10 + N₂ =  100  0,2  =>  N₂ = 10 N  κατακόρυφη προς τα κάτω          Ν₁ , Ν₂  αντίθετες

στην τυχαία θέση :   m₁ g  +  m₂ g  -  k₁ x -  k₂ ( x_0,2  + x )  =  m₁ g  +  m₂ g -  k₁ x -  k₂ ( x_0,2 + x )  =

                             =  10  + 10 -  100 x  -  100 ( 0,2  + x )  =  - 200 x 

το σύστημα θα εκτελέσει Α.Α.Τ.  με σταθερά  D = 200 N/m   και  κυκλική συχνότητα  ω²  =  D / (m₁ + m₂)  =  200 / 2  =>  ω = 10 rad/s     

το πλάτος της ταλάντωσης είναι  Α =  d =  0,2 m      η αρχική φάση είναι  φ = π/2 rad

  x(t)  =  0,2 ημ(10t + π/2)           v(t)  =  2 ημ(10t + π/2)            a(t)  =  - 20 ημ(10t + π/2)  =  - 100 x  

F_ελατ,1  = - k₁ x  =  - 100 x                        F_ελατ,2  = - k₂ ( x_0,2  + x )  =  - 100 ( 0,2  + x )  =  - 20 - 100 x      

U_ελατ,2  =  ½  k₂  ( x_0,2  + x )²  =  ½  100 ( 0,2  + 0,2 )²  =   8 Joule           

για το σώμα (1)  έχουμε :  m₁ g  -  N₁  +  F_ελατ,1  =  m₁ a    =>  10  -  N₁  +  ( - 100 x )  =  1 ( - 100 x )  =>  N₁ = 10 N  σταθερή κατακόρυφη προς τα επάνω     

για το σώμα (2)  έχουμε :  m₂ g  +  N₂  +  F_ελατ,2  =  m₂ a  =>  10  +  N₂  +  ( - 20 - 100 x )  =  1 ( - 100 x )  =>  N₂ = 10 N  σταθερή κατακόρυφη προς τα κάτω      

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

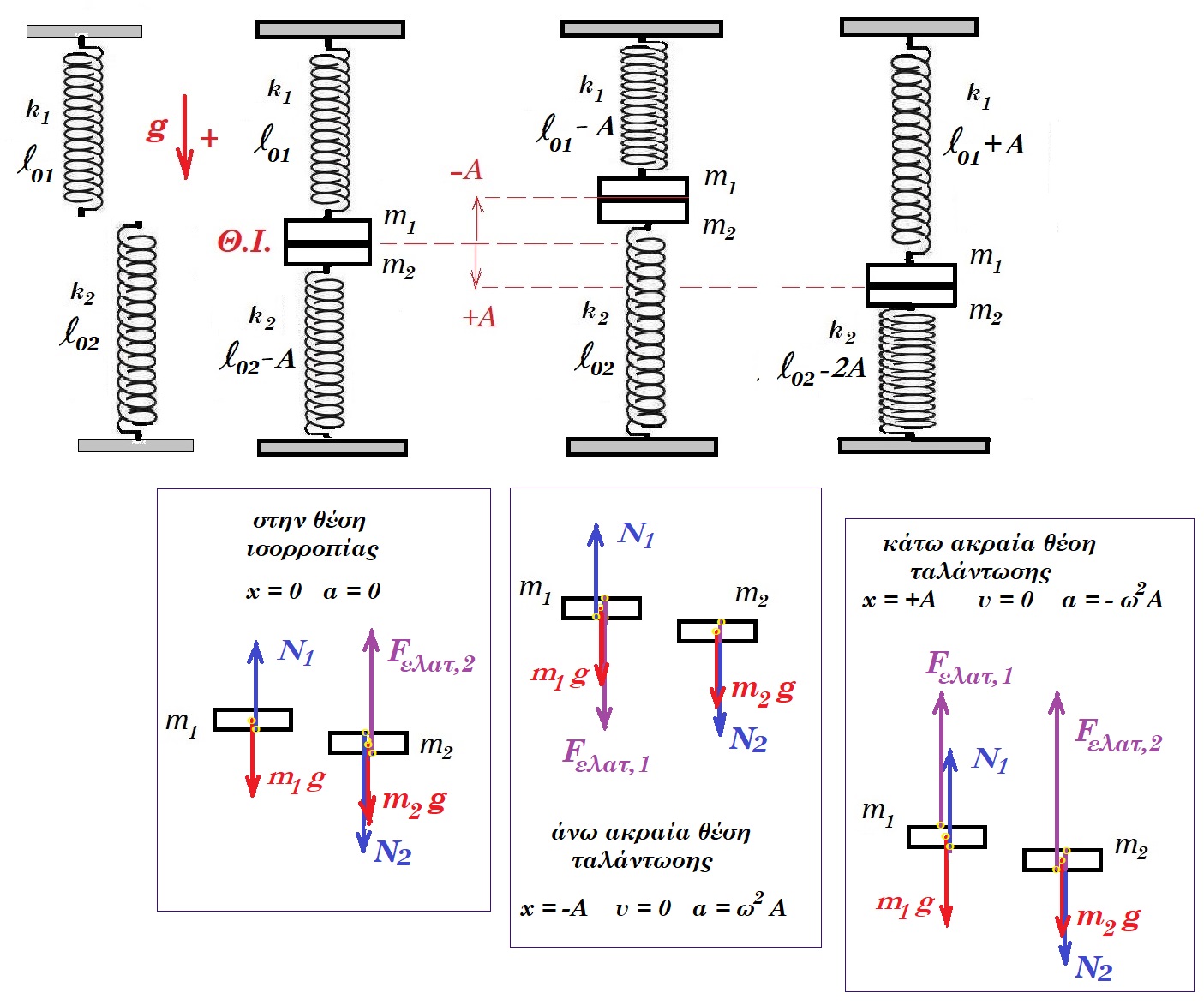
Σώμα Σ1 μάζας m1 = 3 kg ισορροπεί ακίνητο ενώ είναι προσδεμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθερός k=100N/m. Στο πάνω άκρο του ελατηρίου είναι προσδεμένο σώμα Σ2 που ισορροπεί ακίνητο στο κάτω άκρο αβαρούς και μη εκτατού νήματος που το πάνω άκρο του είναι ακλόνητα στερεωμένο σε σημείο της οροφής. Το όριο θραύσης του νήματος είναι Τθραύσ=100Ν. Το Σ1 απέχει από το οριζόντιο επίπεδο απόσταση d = 1,6 m. Τη χρονική στιγμή t0 βάλουμε από το οριζόντιο επίπεδο σφαίρα Σ μάζας m=1kg με κατακόρυφη ταχύτητα μέτρου υ0 = 8 m/s με φορά προς τα πάνω. Το συσσωμάτωμα που δημιουργείται μετά την πλαστική κρούση της σφαίρας Σ με το σώμα Σ1 εκτελεί απλή αρμονική ταλάντωση κατά την διάρκεια της οποίας το νήμα οριακά δεν κόβεται.  Δίνεται g = 10 m/s2.

Να υπολογίσετε:

1) το μέτρο της ταχύτητας του συσσωματώματος αμέσως μετά την δημιουργία του.

2) το πλάτος ταλάντωσης του συσσωματώματος.

3) τη μάζα του σώματος Σ₂.

4) το ρυθμό μεταβολής της δυναμικής ενέργειας του ελατηρίου όταν η τάση του νήματος έχει μέτρο Τ = 50 Ν για 2^η φορά μετά την δημιουργία του συσσωματώματος.

  v²  =  v₀²  -  2 g h =  8²  - 2 10 1,6 =  64  -  32  =  32  =>  v = 4 √2 m/s     

πλαστική κρούση :   u  =  √2 m/s   ταχύτητα συσσωματώματος Σ - Σ₁   

ισορροπία  Σ₁  :  m₁ g = k x₁  =>  30 = 100 x₁  =>  x₁ = 0,3 m  επιμήκυνση     

ισορροπία  Σ₁ - Σ  :  ( m + m₁ ) g = k dx₁  =>  40 = 100 dx₁  =>  dx₁ = 0,4 m  επιμήκυνση      

  k  = ( m + m₁ ) ω²  =>  100 = 4 ω²  =>  ω = 5 rad/s     

το συσσωμάτωμα βρίσκεται σε απομάκρυνση 0,1 m από τη θέση ισορροπίας του κατά την ταλάντωσήτου και έχει ταχύτητα u  =  √2 m/s     

  διατήρηση ενέργειας :  ½  4  (√2)²  +   ½  100  0,1²  =   ½  100  A²  =>  4  +  0,5  =  50  A²  =>  A  =  0,3 m

 x(t)  =  0,3 ημ(5t + φ)  θετική φορά προς τα πάνω     υ(t)  =  1,5 συν(5t + φ)        α(t)  = - 7,5 ημ(5t + φ)

 0,1  =  0,3 ημ(5t + φ)  =>  ημφ  =  1/3      συνφ  =  + 2√2/3     υ = 1,5 ( + 2√2/3 ) =  +√2 m/s  το σώμα ανεβαίνει

  ΣF  =  ( m + m₁ ) a  =>   F_ελατ  -  ( m + m₁ ) g  =  ( m + m₁ ) a  =>  F_ελατ  =  40  +  4 [ - 7,5 ημ(5t + 3π/2) ]  => 

        =>  F_ελατ  =  40  -  30 ημ(5t + φ)        η μέγιστη τιμή του μέτρου της  F_ελατ  είναι 40 + 30 = 70 Ν  όταν το συσσωμάτωμα είναι στο κάτω άκρο της ταλάντωσης  και το ελατήριο είναι επιμηκυμένο κατά 0,7 m = 0,4 + 0,3 

ισορροπία  Σ₂ :   T  -  m₂ g  +  F_ελατ'  =  0  =>   100  -  m₂ 10  -  70   =  0  =>  m₂ = 3 kg     

     T  -  m₂ g  +  F_ελατ'  =  0  =>   T  -  30  +  [ - 40  +  30 ημ(5t + φ) ]  =  0  =>

   =>   T  -  70  +  30 ημ(5t + φ)  =  0  =>   T(t)  =  70  -  30 ημ(5t + φ) 

T  =  70  -  30 ημ(5t + φ)  =>  50  =  70  -  30 ημ(5t + φ)  =>   ημ(5t + φ)  =  2/3      

συν(5t + φ) =  + √5/3   όταν το σώμα ανεβαίνει            συν(5t + φ) =  - √5/3   όταν το σώμα κατεβαίνει    

U_ελατ  =  ½  k  ( x - 0,4 )²        

dU_ελατ / dt =  k  ( x - 0,4 )  v  =  100  [ 0,3 ημ(5t + φ) - 0,4 ]   1,5 συν(5t + φ)  = 

                 =  100  [ 0,3 2/3 - 0,4 ]   1,5  ( - √5/3 )  =   100  [ - 0,2 ]   1,5  ( - √5/3 )  => dU_ελατ / dt =  10√5 J/s   

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

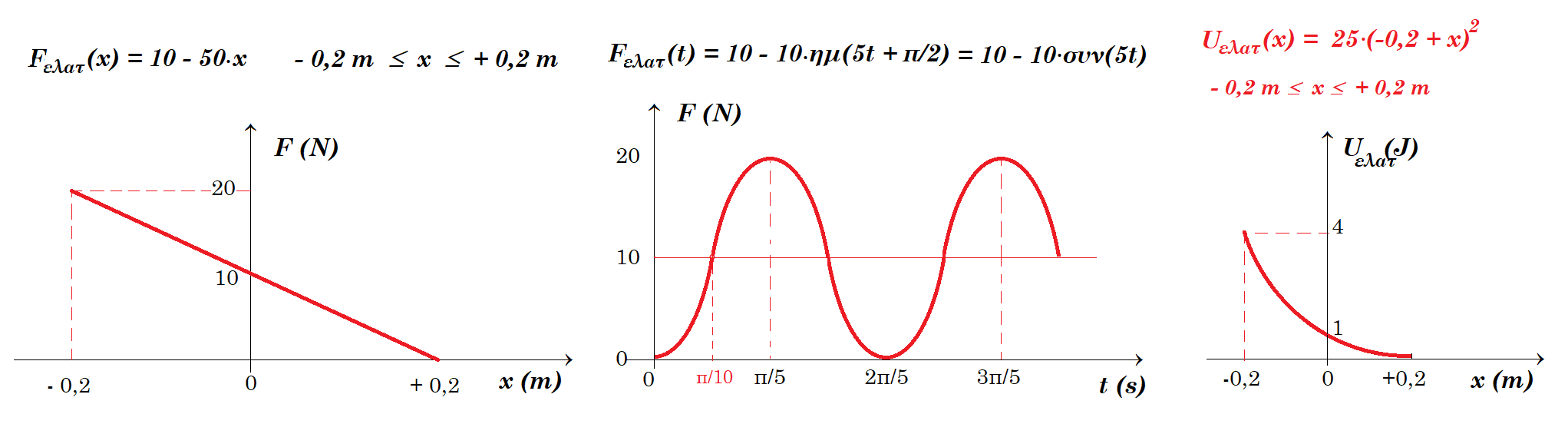
ΘΕΜΑ 2       Θέμα 31670

2.1.  H ταχύτητα του φωτός στο κενό είναι ίση με 𝑐 = 3·10⁸ 𝑚/𝑠. Η εξίσωση που περιγράφει το ηλεκτρικό πεδίο ενός αρμονικού ηλεκτρομαγνητικού κύματος που διαδίδεται στο κενό είναι :

(α)  𝛦 = 30𝜂𝜇2𝜋(6∙10¹⁰𝑡 − 2∙10²𝑥) (𝑆. 𝐼. )
(β)  𝛦 = 30𝜂𝜇2𝜋(8∙10¹⁰𝑡 − 3∙10²𝑥) (𝑆. 𝐼. )
(γ)  𝛦 = 30𝜂𝜇2𝜋(9∙10¹⁰𝑡 − 4∙10²𝑥) (𝑆. 𝐼. )
2.1.Α. Να επιλέξετε την ορθή απάντηση.                  Μονάδες 4
2.1.B. Να αιτιολογήσετε την επιλογή σας.                Μονάδες 8

2.2.  Ένα πρωτόνιο (μάζας 𝑚_𝑝, ηλεκτρικού φορτίου 𝑞_𝑝) και ένα σωματίδιο άλφα (μάζας 𝑚_𝛼 = 4𝑚_𝑝,
ηλεκτρικού φορτίου 𝑞_𝑎 = 2𝑞_𝑝) επιταχύνονται από την ηρεμία με την ίδια διαφορά δυναμικού 𝑉. Αν το μήκος κύματος de Broglie του πρωτονίου είναι 0,4 𝑛𝑚, το αντίστοιχο μήκος κύματος de Broglie για το σωματίδιο άλφα είναι:
(α) 0,1 𝑛𝑚 ,    (β) 0,8√2 𝑛𝑚 ,    (γ) 0,1√2 𝑛𝑚
2.2.Α. Να επιλέξετε την ορθή απάντηση.               Μονάδες 4
2.2.B. Να αιτιολογήσετε την επιλογή σας.            Μονάδες 9

ΘΕΜΑ 4    Θέμα #30074

Μια αγώγιμη ράβδος μήκους ℓ = 40 cm μπορεί να ολισθαίνει ελεύθερα σε δύο παράλληλες αγώγιμες ράβδους. Οι παράλληλες ράβδοι και η ράβδος μήκους ℓ έχουν αμελητέα αντίσταση.  Δύο αντιστάτες με αντίσταση R₁ = 2 Ω και R₂ = 4 Ω συνδέονται στα άκρα των παράλληλων ράβδων όπως φαίνεται στο παρακάτω σχήμα. Το σύστημα βρίσκεται στο εσωτερικό ομογενούς μαγνητικού πεδίου έντασης B = 2,5 T,  του οποίου οι δυναμικές γραμμές κατευθύνεται κάθετα προς τη σελίδα.  Μία οριζόντια εξωτερική δύναμη F ασκείται κάθετα στην ράβδο και στο μαγνητικό πεδίο προς τα αριστερά με αποτέλεσμα η ράβδος να κινείται με σταθερή ταχύτητα μέτρου υ = 8 m/s.

Να απαντήσετε στα επόμενα ερωτήματα, τα οποία αναφέρονται στο χρονικό διάστημα της κίνησης της ράβδου με σταθερή ταχύτητα πριν φτάσει στην αντίσταση R₁.
4.1.  Να υπολογίσετε την ένταση του ρεύματος που διαρρέει κάθε αντιστάτη.       Μονάδες 6
4.2.  Να βρείτε την ενέργεια που καταναλώνει καθεμιά από τις αντιστάσεις R₁ και R₂ όταν η ράβδος μετατοπιστεί κατά d = 2m.                                                                                  Μονάδες 6
4.3.  Να υπολογίσετε την εξωτερική δύναμη F που δέχεται η ράβδος.                      Μονάδες 6
4.4.  Ποιο ποσοστό του προσφερόμενου ρυθμού ενέργειας από την δύναμη F στην ράβδο, καταναλώνεται στον αντιστάτη R₂;                                                                                 Μονάδες 7