Ε.Ε.Φ.  2020

ΘΕΜΑ A1

Σημειακό σώμα (Σ₁)  μάζας m₁ = m  έχει κινητική ενέργεια  Κ₁  και κάνει κεντρική ελαστική κρούση με άλλο ακίνητο σημειακό σώμα (Σ₂)  τριπλάσιας μάζας m₂ = 3m. 

(A)   Μετά την κρούση, η κινητική ενέργεια του σώματος (Σ₂)  ισούται με :

                 α.  Κ₁/2          β.  3Κ₁/4         γ.  3Κ₁/8           δ.  2Κ₁/3

(B)   Κατά την διάρκεια της κρούσης, η μεταβολή της ορμής του σώματος (Σ₁)  ισούται με :

                 α.  √( 3/2 m K₁ )         β.  - √( 3/2 m K₁ )         γ.  - √( 1/2 m K₁ )         δ.  √( m K₁ )         

          Κ₁ = ½ m₁ v₁²  =  p₁² / 2m₁  =  p₁² / 2m  =>   p₁ = √( 2m K₁ )    

 v₁' = v₁ (m₁ - m₂) / (m₁ + m₂)  +  2 m₂ v₂ / (m₁ + m₂)   =  v₁ (m - 3m) / (m + 3m)  =  - v₁/2

 v₂' = v₂ (m₂ - m₂1) / (m₁ + m₂)  +  2 m₁ v₁ / (m₁ + m₂)  =  2 m v₁ / (m + 3m)  =  + v₁/2  

 Κ₁' = ½ m₁  (v₁')²  =  ½ m v₁² / 4  =  Κ₁/4       

Κ₂' = ½ m₂  (v₂')²  =  ½  3m v₁² / 4  =  3Κ₁/4       

η μεταβολή της ορμής του σώματος (Σ₁)  κατά την διάρκεια της κρούσης είναι :

        Δp₁  =  p₁' - p₁  =  m (- v₁/2)  -  m v₁  =  - 3/2 m v₁  =  - √( 3/2 m K₁ )    

η μεταβολή της ορμής του σώματος (Σ₂)  κατά την διάρκεια της κρούσης είναι :

        Δp₂  =  p₂' - p₂  =  3m  v₂/2  -   0  =   1/2  3m  v₁  =  √( 3/2 m K₁ )         

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΕΜΑ A2

Σε οριζόντιο έδαφος είναι στερεωμένο κατακόρυφα ιδανικό ελατήριο, με σταθερά  k = 100 N/m. Πάνω στο ελατήριο ισορροπεί, χωρίς να είναι δεμένο, μικρό σώμα μάζας m = 4 kg.  Από τη θέση ισορροπίας, πιέζουμε το σώμα  προς τα κάτω κατά d = 0,8 m και τη χρονική στιγμή t = 0 το αφήνουμε ελεύθερο, με αποτέλεσμα να κινηθεί προς τα πάνω κατά μήκος του άξονα του ελατηρίου. Δίνεται το μέτρο της επιτάχυνσης της βαρύτητας:  g = 10 m/s².   Θεωρήστε ως θετική τη φορά προς τα πάνω και για τις πράξεις :   π = 3     √3 = 1,7        

Α.  Η χρονική στιγμή που θα μηδενιστεί η δυναμική ενέργεια του ελατηρίου για πρώτη φορά είναι:

α.  0,17 s              β.  0,2 s           γ.  0,34 s             δ.  0,4 s

Β.  Η χρονική στιγμή που το σώμα θα φτάσει στο μέγιστο δυνατό ύψος για πρώτη φορά είναι:

α.  0,57 s              β.  0,6 s           γ.  0,74 s             δ.  0,8 s

Γ.  Βρείτε σε πόσο μέγιστο ύψος φθάνει το σώμα για 1η φορά μετά τη χρονική στιγμή t = 0.

(A) ισορροπία σώματος επάνω στο ελατήριο       m g = k x₀  =>  4  10  =  100  x₀  =>  x₀ = 0,4 m  συσπείρωση  (- 0,4m) 

όταν πιέσουμε το σώμα προς τα κάτω κατά d = 0,8 m  το ελατήριο έχει συσπειρωθεί κατά  1,2 m    και έχει αποθηκεύσει δυναμική ενέργεια  U =  ½ k x²  =  ½ 100  1,2²  =  72 J           

το σώμα θα εκτελέσει Α.Α.Τ. με πλάτος  d = 0,8 m  και συχνότητα  ω = √( k/m ) = √( 100/4 ) = 5 rad/s ,  f = 5/2π Hz

 Τ = 1/f  =  2π/5 s   το σώμα θα φθάσει στη θέση ισορροπίας του μετά από χρόνο :  T/4 = 2π/20 s = π/10 = 3/10 = 0,3 s 

            x(t) =  0,8 ημ(5t + 3π/2)                υ(t) =  4 συν(5t + 3π/2)                     x(t) =  - 20 ημ(5t + 3π/2) 

η δυναμική ενέργεια του ελατηρίου θα μηδενισθεί όταν αποκτήσει το φυσικό του μήκος  δηλαδή όταν η απομάκρυνση του σώματος από τη θέσει ισορροπίας γίνει  x = + 0,4 m  =>   0,8 ημ(5t + 3π/2)  =  + 0,4  =>  ημ(5t + 3π/2) = +1/2 

  =>    ημ(5t + 3π/2)  =  ημ(π/6)   ή   ημ(5π/6)     

ημ(5t + 3π/2) = ημ(π/6)  =>  5t + 3π/2  =  2Νπ  + π/6   =>  5t  =  2Νπ  -  8π/6  =>  t = 2Νπ/5 - 8π/30    Ν = 1, 2, ... 

 Ν = 1   t = 2Νπ/5 - 8π/30  = 2π/5 - 8π/30 = 4π/30 =  4 3 / 30 = 0,4 s     ( 1η φορά )

         συν(5t + 3π/2)  =  συν(π/6) = √3/2 > 0     υ = 4 √3/2 = 2 √3 m/s > 0  το σώμα κινείται προς τα επάνω

ημ(5t + 3π/2) = ημ(5π/6)  =>  5t + 3π/2  =  2Νπ  + 5π/6   =>  5t  =  2Νπ - 4π/6  =>  t = 2Νπ/5 - 4π/30   Ν = 1, 2, ... 

Ν = 1   t = 2Νπ/5 - 4π/30  = 2π/5 - 4π/30 = 8π/30  =  8 3 / 30 = 0,8 s     ( 2η φορά )

    συν(5t + 3π/2)  =  συν(5π/6) = - √3/2 < 0     υ = 4 (- √3/2 ) = - 2 √3 m/s < 0  το σώμα κινείται προς τα κάτω 

(B)  μετά το σώμα κατά την κίνησή του  δέχεται μόνο την δύναμη βαρύτητας  θα εκτελέσει κατακόρυφη βολή προς τα επάνω  με αρχική ταχύτητα  v₀ = 2 √3 m/s = 2 1,7 m/s = 3,4 m/s     v = v₀ - g t  =>  0 =  3,4 - 10 t => t = 0,34 s 

   h =  ½ g t²  =  ½  10  0,34²  =  0,578 m

το σώμα θα φθάσει στο μέγιστο ύψος μετά από   0,4 s  +  0,34 s  =  0,74 s

(Γ)  v₀ = 2 √3 m/s        v = v₀ - g t  =>  0 = 2 √3 - 10 t  => t = 0,2 √3 s         h = ½ g t²  = ½ 10  ( 0,2 √3 )² = 0,6 m   

το μέγιστο ύψος που φθάνει το σώμα είναι :   Α  +  Α/2  +  h  =  0,8  +  0,4  +  0,578 = 1,778 m       1,2 + 0,6 = 1,8 m

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΕΜΑ Β1

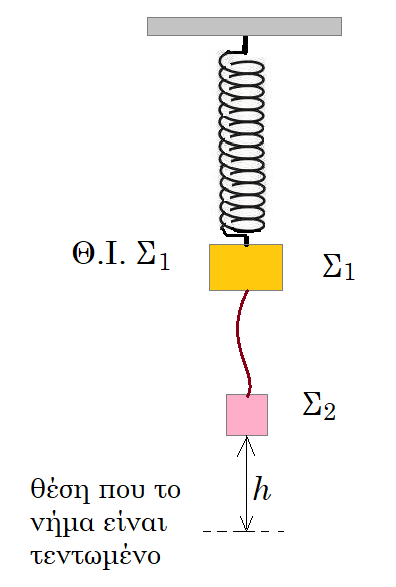Τα σώματα μικρών διαστάσεων Σ1 και Σ2 του σχήματος έχουν μάζες m1 και m2 αντίστοιχα με m1 = 2m2   και είναι δεμένα μεταξύ τους με αβαρές μη εκτατό νήμα. Το σώμα Σ1 είναι δεμένο στο ένα άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, το άλλο άκρο του οποίου είναι στερεωμένο ακλόνητα σε οροφή. Το σώμα Σ1 ισορροπεί, ενώ διατηρούμε το νήμα χαλαρό, όπως φαίνεται στο σχήμα. Το σώμα Σ2 απέχει κατακόρυφη απόσταση h από το σημείο που θα βρισκόταν η κάτω άκρη του νήματος, αν αυτό ήταν τεντωμένο. Κάποια χρονική στιγμή αφήνουμε ελεύθερο το σώμα Σ2. Αν g το μέτρο της επιτάχυνσης της βαρύτητας, τότε η μέγιστη επιτρεπτή τιμή της απόστασης h ώστε το σύστημα Σ1-Σ2 να εκτελεί απλή αρμονική ταλάντωση, με το νήμα να παραμένει συνεχώς κατακόρυφο και τεντωμένο, είναι: α. 12m2g/k       β.  m2g/k        γ.  6m2g/k       δ. 3m2g/k

  θέση ισορροπίας Σ₁ :    m₁ g = k x₁  =>    m₁ g / k = x₁  (1)   επιμήκυνση ελατηρίου

αφήνουμε το Σ₂  ελεύθερο να κινηθεί   εκτελεί ελεύθερη πτώση :   h =  ½ g t²  =>  √(2h/g) = t       v₂ = gt = √(2gh)  (2)

 διατήρηση ορμής :    m₂ v₂ = (m₁ + m₂) u  =>  m₂ v₂ = (2m₂ + m₂) u  =>  v₂/3  =  u   (3)   κοινή ταχύτητα των δύο σωμάτων αμέσως μόλις τεντώσει το νήμα ( σαν πλαστική κρούση )

  θέση ισορροπίας Σ₁ - Σ₂ :    (m₁ + m₂) g = k x_1,2  =>    3m₂ g / k = x_1,2   (4)   επιμήκυνση ελατηρίου

όταν τεντώσει το νήμα τα σώματα απέχουν από τη νέα θέση ισορροπίας κατακόρυφη απόσταση :   x_1,2  -  x₁  =  3m₂ g / k  -  m₁ g / k  =  3m₂ g / k  -  2m₂ g / k  =  m₂g/k    τα σώματα εκείνη τη στιγμή έχουν κοινή ταχύτητα   u = v₂/3   κατακόρυφη προς τα κάτω

τα σώματα θα εκτελέσουν Α.Α.Τ.   με συχνότητα   και   μέγιστο πλάτος ταλάντωσης  Α = x_1,2  = 3m₂ g / k   διότι εάν είναι μεγαλύτερο τότε το νήμα θα χαλαρώσει όταν κινούνται προς τα επάνω  ( το Σ₁  εκτός του βάρους του δέχεται δύναμη από το ελατήριο το οποίο συσπειρώνεται,  ενώ το Σ₂  δεν δέχεται άλλη δύναμη εκτός του βάρους του )

διατήρηση ενέργειας για την ταλάντωση : 

  ½ k A²  =   ½ k ( x_1,2  -  x₁ )²   +    ½  m_1,2  u²    =>    k ( 3m₂ g / k )²  =   k ( m₂g/k )²   +   3 m₂  ( v₂/3 )²    => 

=>   8  k ( m₂ g / k )²  =  3 m₂  2gh/9     =>   h  =  12 m₂ g / k         

εάν το ύψος  h  είναι μεγαλύτερο  το Σ₂  θα έχει αποκτήσει μεγαλύτερη ταχύτητα τη στιγμή που το νήμα τεντώνει  άρα τα σώματα μετά θα αποκτήσουν μεγαλύτερη ταχύτητα   με συνέπεια το πλάτος ταλάντωσης να είναι μεγαλύτερο από  Α = x_1,2  = 3m₂ g / k 

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΕΜΑ Β2
Σώμα μάζας m=700g εκτελεί φθίνουσα γραμμική μηχανική ταλάντωση με σταθερά επαναφοράς D = 4π² / ln 2 N/m, εξαιτίας αντιτιθέμενης δύναμης της μορφής  F ' = - b υ,  όπου υ η ταχύτητα του σώματος και b η σταθερά απόσβεσης.  Το πλάτος Α της ταλάντωσης δίνεται από τον τύπο Α = Α₀ e^-Λt, όπου  Λ = 1 s^-1  και  Α₀ = 80 cm.  Από τη χρονική στιγμή t₁ = ln2 s  έως τη χρονική στιγμή t₂ = 2ln2 s, όπως επίσης και από τη χρονική στιγμή   t₃ = 3ln2 s  έως τη χρονική στιγμή   t₄ = 4ln2 s  ασκείται στο σώμα επιπλέον δύναμη  αλγεβρικής τιμής  F  = + b υ.  Αν  π² = 10   και ln2=0,7 ,  το συνολικό έργο της δύναμης  F   είναι :               2,4/ln2 J            3/ln2 J                12,8/ln2 J          12π/ln2 J  

Α = Α₀ e^-Λt              t₁= ln2 s     Α₁ = Α₀ e^-ln2 = A₀/2            t₂ = 2ln2 s    Α₂ = Α₀ e^-2ln2 = A₀/4 

  t₃ = 3ln2 s    Α₃ = Α₀ e^-3ln2 = A₀/8             t₄ = 4ln2 s    Α₄ = Α₀ e^-4ln2 = A₀/16          

          ln2              2 ln2              3 ln2            4 ln2

A₀      A₀/2             A₀/4              A₀/8              A₀/16            

A₀      A₀/2             A₀/2              A₀/4             A₀/4            

½ D (A₀/4)²  -  ½ D (A₀/16)²  =   ½ D A₀²/16  -  ½ D A₀²/256  =  ½  4π²/ln2   15/256   A₀²   =

    =  ½  40/0,7   15/256   0,8²      

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΕΜΑ Γ1

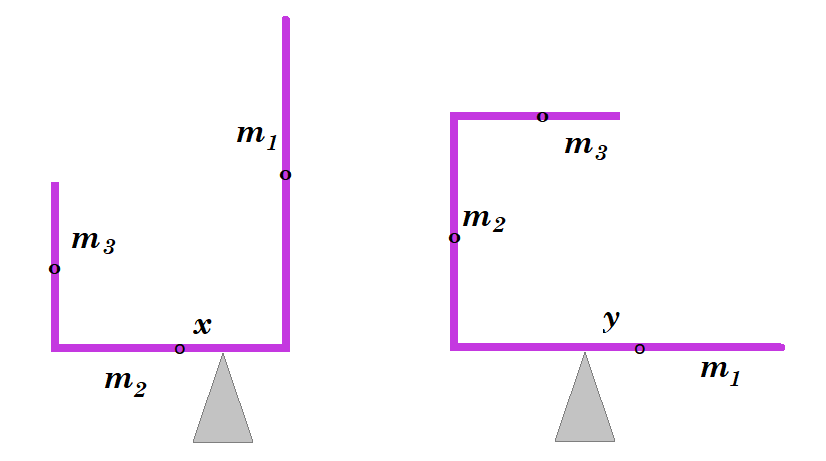
     l₁ = 3 m     l₂ = 2 m         l₃ = 1 m       x = y   

 α.  m₁ = 5 kg    m₂ = 1 kg    m₃ = 2 kg            β.  m₁ = 5 kg    m₂ = 2 kg    m₃ = 1 kg  

 γ.  m₁ = 4 kg    m₂ = 2 kg    m₃ = 3 kg            δ.    m₁ = 3 kg    m₂ = 2 kg    m₃ = 1 kg  

Στ = 0  =>  m₃ g (x + l₂/2)  +  m₂ g x  -  m₁ g (l₂/2 - x)  =  0  =>  m₃ g (x + 1)  +  m₂ g x  -  m₁ g (1 - x)  =  0  => 

          =>  ( m₃ + m₂ + m₁ ) x  =   m₁  -  m₃   (1)

Στ = 0  =>  m₃ g (l₁/2  - y - l₃/2)  +  m₂ g (l₁/2  - y)  - m₁ g y  =  0  =>  m₃ (1 - y)  +  m₂ (3/2  - y)  -  m₁  y  =  0 => 

          =>  ( m₃ + m₂ + m₁ ) y  =   m₃  +  3/2 m₂     (2)

 (1) , (2) =>    m₁  -  m₃  =   m₃  +  3/2 m₂   =>   m₁   =   2m₃  +  3/2 m₂        (β)

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΕΜΑ Γ3

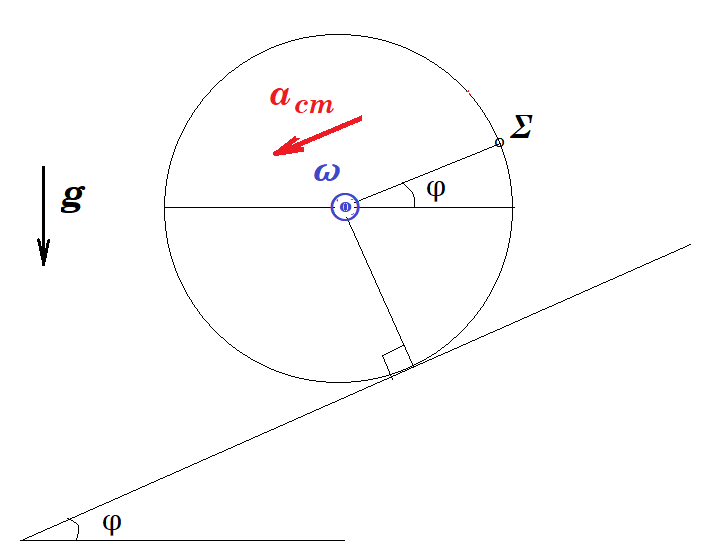Ομογενής δίσκος, ακτίνας R = 1 m , αφήνεται ελεύθερος πάνω σε κεκλιμένο επίπεδο. Ο δίσκος ξεκινά να κυλίεται χωρίς να ολισθαίνει, με επιτάχυνση κέντρου μάζας μέτρου α_cm =  2 m/s².  Έστω Σ το σημείο της περιφέρειας του δίσκου, του οποίου η επιβατική ακτίνα είναι παράλληλη στη
διεύθυνση του κεκλιμένου δαπέδου όπως φαίνεται στο σχήμα. Το μέτρο της επιτάχυνσης του
σημείου Σ, τη στιγμή όπου το μέτρο της γωνιακής ταχύτητας του δίσκου είναι ίσο με 1 rad/s θα είναι:
α.  √5 m/s²             β.  2√2 m/s²              γ.  √13 m/s²               δ.  √17 m/s²                                

            v = ω R = 1 rad/s  1 m = 1 m/s                    a_cm  =  α_γ R  =>  2 m/s² = α_γ 1 m  =>  α_γ = 2 rad/s²  

    v = a_cm t =>  1 m/s = 2 m/s² t  =>  t = 0,5 s           ω = α_γ t  =>  1 rad/s  =  α_γ  0,5 s  => α_γ = 2 rad/s²     

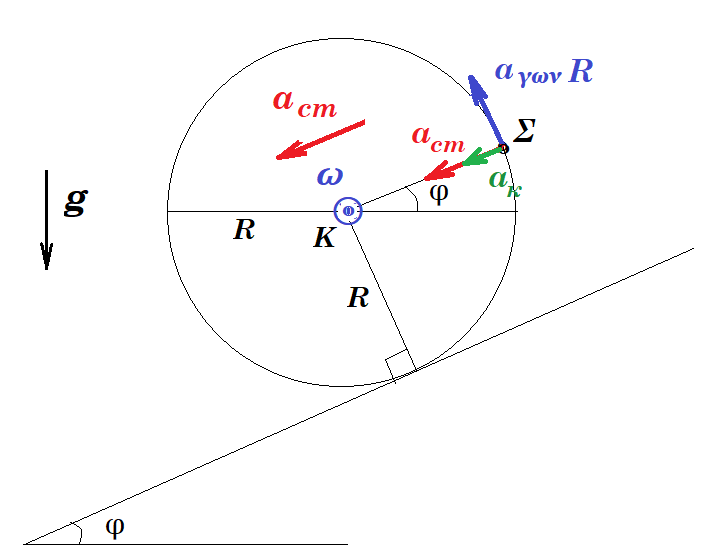
κεντρομόλος επιτάχυνση :  α_κ  =  v²/R =  (1 m/s)² / 1 m = 1 m/s²   

  a²  =  ( a_cm + α_κ )²  +  a_γ² R²  = ( 2 + 1 )²  +  2² 1²  =  13  =>  a  =  √13 m/s²  

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΕΜΑ Δ1

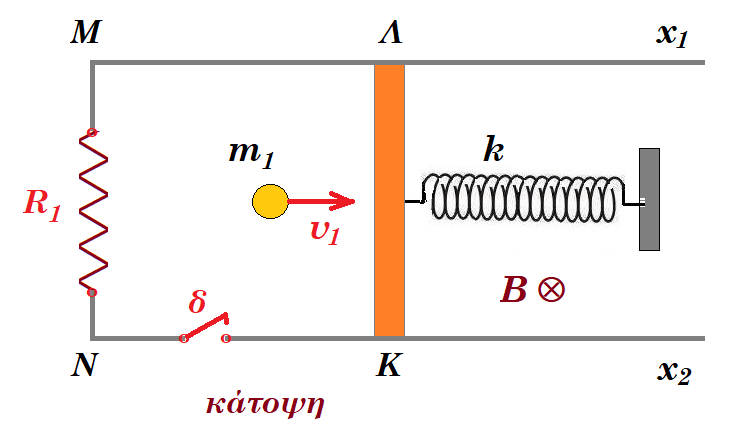
Σφαίρα Σ₁  μάζας m₁ = 0,5 kg  κινείται κατά μήκος λείου οριζοντίου δαπέδου με ταχύτητα  υ₁ = 6 m/s  και τη χρονική στιγμή t=0  συγκρούεται κεντρικά και ελαστικά  στο μέσον ακίνητου ομογενούς πρισματικού αγωγού ΚΛ μάζας  m₂ = 2,5 kg,  μήκους  L = 1m  και αντίστασης  R_ΚΛ = 1Ω.   Το σώμα Σ₁ αμέσως μετά την κρούση απομακρύνεται και δεν επηρεάζει τη διάταξη.  Ο αγωγός είναι δεμένος στο ένα άκρο ιδανικού οριζόντιου ελατηρίου σταθερός K = 250 N/m  το άλλο άκρο του οποίου είναι στερεωμένο ακλόνητα, όπως φαίνεται στο σχήμα.  Ο αγωγός ΚΛ αμέσως μετά την κρούση, αρχίζει να εκτελεί απλή αρμονική ταλάντωση ολισθαίνοντας κατά μήκος δύο παράλληλων οριζοντίων αγωγών Μx₁ και Nx₂, αμελητέας ωμικής αντίστασης, παραμένοντας συνεχώς κάθετος σ' αυτούς.  Τα άκρα Μ και Ν των δύο αγωγών συνδέονται μέσω αντιστάτη αντίστασης R₁ = 1,5 Ω  και ανοικτού διακόπτη δ, όπως φαίνεται στο σχήμα.  Όλη η διάταξη των αγωγών βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο έντασης μέτρου Β = 2 Τ, του οποίου οι μαγνητικές γραμμές είναι κάθετες στο επίπεδό των αγωγών.  Τη στιγμή που ο αγωγός έχει διανύσει απόσταση S=1,4 m κλείνουμε απότομα τον διακόπτη.
Α.  Θεωρώντας ως θετική τη φορά προς τα δεξιά  ( δηλαδή τη φορά της ταχύτητας υ₁ )  η θέση που βρίσκεται ο αγωγός τη στιγμή που κλείνουμε το διακόπτη :
α.  είναι η θέση ισορροπίας της ταλάντωσης
β.  είναι το θετικό άκρο της ταλάντωσης
γ.  είναι το αρνητικό άκρο της ταλάντωσης
δ.  απέχει 0,1 m από τη θέση ισορροπίας της ταλάντωσης

Β.  Το ποσό θερμότητας που εκλύεται από τον αγωγό ΚΛ μέχρι να ακινητοποιηθεί πλήρως ο αγωγός ισούται με :
α.  0,2 J        β.  0,5 J             γ.  2 J             δ.  5 J 

Γ.  Βρείτε στη διάρκεια της κίνησης του αγωγού πόσο φορτίο μετατοπίζεται, από μία διατομή του.

(Α)       διατήρηση ορμής κατά την κρούση :  m₁ v₁  =  m₁ v₁'  +  m₂ v₂' 

v₁' = v₁ (m₁ - m₂) / (m₁ + m₂)  +  2 m₂ v₂ / (m₁ + m₂)   =  6 (0,5 - 2,5) / (0,5 + 2,5)  =  - 4 m/s 

 v₂' = v₂ (m₂ - m₂1) / (m₁ + m₂)  +  2 m₁ v₁ / (m₁ + m₂)  =  2 0,5  6 / (0,5 + 2,5)  =  + 2 m/s        

η ράβδος ΚΛ  βρίσκεται σε θέση ισορροπίας,  το ελατήριο έχει το φυσικό του μήκος  και  αμέσως μετά την ελαστική κρούση εκτελεί Α.Α.Τ.  με μέγιστη ταχύτηα  υ =  2 m/s   

τη στιγμή  t = 0  η ταχύτητα έχει κατεύθυνση προς τα δεξιά ( θετική )   

   x(t)  =  A ημωt             ω² = k/m₂ =  250 / 2,5 = 100 =>  ω = 10 rad/s          T = 2π/ω = 2π/10 = π/5 s

  v = ω A  =>  2 m/s  =  10 rad/s  A  =>  A = 0,2 m  πλάτος της ταλάντωσης της ράβδου ΚΛ 

  άρα   x(t)  =  0,2 ημ(10t           υ(t)  =  2 συν10t            α(t)  =  - 20 ημ10t         

όταν διανύσει απόσταση  1,4 m =  7  0,2 m  =  7 Α   θα βρίσκεται σε απομάκρυνση  - Α = - 0,2 m      (γ)     κλείνουμε τον διακόπτη

(Β)    στη συνέχεια  η ράβδος ΚΛ  κινείται μέσα σε μαγνητικό πεδίο εντάσεως Β  οπότε τα ηλεκτρόνιά της δέχονται δύναμη Lorentz  και μετατοπίζονται προς το άκρο Κ  το οποίο φορτίζεται αρνητικά  ενώ το άκρο Λ  φορτίζεται θετικά   

έτσι επάγεται τάση στα άκρα της ράβδου  Ε_επαγ =  B v l  =  i ( R₁ + R_ΚΛ )   νόμος του Ohm για κλειστό κύκλωμα

η ράβδος διαρρέεται από ρεύμα εντάσεως  i  οπότε δέχεται δύναμη Laplace  μέτρου  F_L = B i l  = B l B v l / ( R₁ + R_ΚΛ ) =>  F_L =  B² l² v / ( R₁ + R_ΚΛ ) =>  F_L =  2² 1² v / ( 1,5 + 1 ) =>  F_L =  1,6 v     αντίρροπη της ταχύτητας

η ράβδος ΚΛ θα εκτελέσει φθίνουσα ταλάντωση :   A = A₀ e^{- Λt}  =  A₀  e^{-b/2m t}  =  0,2m  e^{-1,6/5 t}  =  0,2m  e^{-0,32 t}   

αρχικά το ελατήριο είναι επιμηκυμένο κατά  Α₀ = 0,2m   έχει δυναμική ενέργεια   U_ελατ = ½ k A₀² = ½  250  0,2² = 5 J

η οποία καταναλώνεται στις αντιστάσεις  μέχρι να σταματήσει η ράβδος να κινείται

   P₁  +  P_KΛ  =  i² (R₁ + R_ΚΛ)              Q_ΚΛ  =  U_ελατ  R_ΚΛ / (R₁ + R_ΚΛ)  =  5J  1Ω / 2,5Ω  =>  Q_ΚΛ = 2 J

  (Γ)       Η ράβδος θα σταματήσει να κινείται στη θέση ισορροπίας, όταν η ενέργεια της ταλάντωσης θα γίνει θερμότητα Joule. Τότε, η ολική μετατόπιση έχει μέτρο  Α₀  και η μεταβολή της μαγνητικής ροής θα είναι, απολύτως, ΔΦ = B l A₀
Το ηλεκτρικό φορτίο που θα μετατοπισθεί μέσω μιας διατομής του αγωγού θα είναι:
  q  =  ΔΦ / (R₁ + R_ΚΛ)  =  B l A₀ / (R₁ + R_ΚΛ)  = 2 1 0,2 / 2,5 = 4/25 Coulomb  =  0,16 C

μελέτη της κίνησης του αγωγού ΚΛ :

ΣF = m₂ a  =>  F_ελατ  -  F_L  =  m₂ a  =>  - k x  -  B²l²v / (R₁ + R_ΚΛ)  =  m₂ a  =>  - 250 x  -  1,6 v  =  2,5 a  =>  

=>  250 x  -  1,6 dx/dt  =  2,5 d²x/dt²  =>   d²x/dt²  +   0,64 dx/dt   +  100 x  =  0  

το χαρακτηριστικό πολυώνυμο :    ρ²  +   0,64 ρ  +  100  =  0        

    Δ = 0,64² -  400 = - 399,6 = j² 399,6               √Δ = 19,99 j     μιγαδικός

          ρ₁ =  (- β + √Δ) / 2α  =  ( - 0,64 + 19,99 j ) / 2  =  - 0,32 + 9,995 j

          ρ₂ =  (- β - √Δ) / 2α  =  ( - 0,64 - 19,99 j ) / 2  =  - 0,32 - 9,995 j

   x(t)  =  c₁ e ^{ρ₁ t}  +  c₂ e ^{ρ₂ t}  =  c₁ e^{( - 0,32 + 9,995 j ) t}  +  c₂ e^{( - 0,32 - 9,995 j ) t}  =

 =  c₁ e ^{- 0,32 t} ( συν 9,995 t  +  j ημ 9,995 t )  +  c₂ e ^{- 0,32 t} ( συν 9,995 t  -  j ημ 9,995 t ) =

 = (c₁ + c₂) e ^{- 0,32 t}  συν 9,995 t  +  j (c₁ - c₂) e ^{- 0,32 t}  ημ 9,995 t  =

 = A₀ e ^{- 0,32 t}  συν 9,995 t  +  B₀ e ^{- 0,32 t}  ημ 9,995 t 

x(t) = 0,2  e ^{- 0,32 t}  συν 9,995 t              x(0) = 0,2  e⁰ συν(0) = 0,2  1  1 = 0,2 m

εξίσωση απομάκρυνσης της ράβδου ΚΛ  από τη θέση ισορροπίας της   συναρτήσει του χρόνου

υ(t) = - 0,32 0,2 e ^{- 0,32 t}  συν 9,995t   -  0,2 e ^{- 0,32 t}  9,995  ημ 9,995t   

υ(t) = - 0,064  e ^{- 0,32 t}  συν 9,995 t   -   1,999  e ^{- 0,32 t}  ημ 9,995 t 

    εξίσωση της ταχύτητας της ράβδου ΚΛ  συναρτήσει του χρόνου

  i =  Blv / (R₁ + R_ΚΛ) =  2 1 v / (1 + 1,5) =>  i(t) = 0,8 v(t)  => 

 =>  i(t) = 0,8  { - 0,064  e ^{- 0,32 t}  συν 9,995 t   -   1,999  e ^{- 0,32 t}  ημ 9,995 t }  =>

 =>  i(t) =  - 0,0512  e ^{- 0,32 t}  συν 9,995 t   -   1,5992  e ^{- 0,32 t}  ημ 9,995 t   

  v = dx / dt 

i = dq / dt  =>  dq = i dt =>  dq = Blv / (R₁ + R_ΚΛ)  dt   =>  dq = Bl / (R₁ + R_ΚΛ)  v dt  => 

           =>  dq = 0,8  dx  =>    q(t) - q(0)  = 0,8 [ x(t) - x(0) ]  =>         q(0) = 0     x(0) = 0,2m

          =>  q(t)   = 0,8 [ 0,2  e ^{- 0,32 t}  συν 9,995 t   -   0,2 ]   =>   

          =>  q(t)   =  0,16  e ^{- 0,32 t}  συν 9,995 t   -   0,16            

  όταν  t ® ¥   τότε   q  =  - 0,16 C         διότι       e^-¥ = 0