Ε.Ε.Φ.    2021  

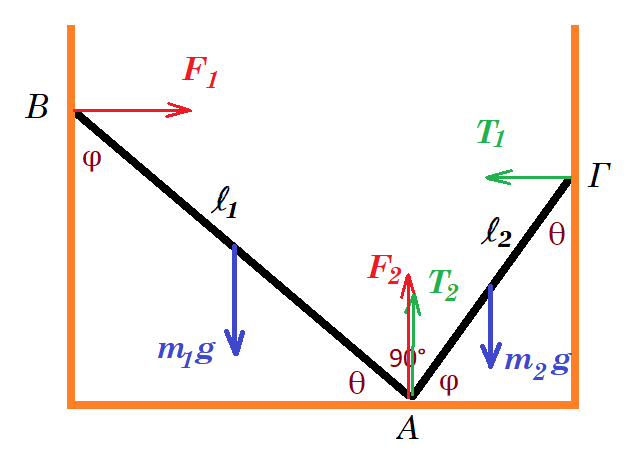
Οι ράβδοι ΑΒ και ΑΓ ισορροπούν εφαπτόμενες σε λεία κατακόρυφα τοιχώματα και μεταξύ τους στο κοινό τους άκρο Α πάνω σε λείο οριζόντιο δάπεδο, σχηματίζοντας γωνία 90°. Οι ράβδοι έχουν μάζες m₁, m₂  και μήκη  l₁, l₂  αντίστοιχα. Δεδομένου ότι η τομή της επαφής των ράβδων είναι κατακόρυφη, η απόσταση των κατακόρυφων τοιχωμάτων είναι :

    α)  ( l₁  m₂  +  l₂  m₁ ) / (m₁+ m₂)            β)  ( l₁  √m₂  +  l₂  √m₁ ) / √(m₁+ m₂)  

    γ)  ( l₁  √m₂  -  l₂  √m₁ ) / √(m₁+ m₂)      δ)  ( l₁  m₂  -  l₂  m₁ ) / (m₁+ m₂)  

     φ + θ = 90°       ημφ = συνθ      συνφ = ημθ                F₁  =  Τ₁              F₂ + Τ₂  =  m₁g + m₂g

ροπές ως προς Α :   m₁ g l₁/2 συνθ   -  F₁ l₁ ημθ   =  0   => m₁ g 1/2 συνθ   =  F₁ ημθ        

                          m₂ g l₂/2 συνφ   -  Τ₁ l₂ ημφ   =  0   =>    m₂ g 1/2 ημθ   =  Τ₁ συνθ          

        m₁  συν²θ  =  m₂  ημ²θ   =>  εφ²θ  = m₁ / m₂    

   ημ²θ + συν²θ = 1  =>  εφ²θ + 1 = 1/συν²θ  =>  συν²θ = 1 / (1 + εφ²θ) = 1 / (1 + m₁ / m₂) =  m₂ / (m₁+ m₂)

   ημ²θ + συν²θ = 1  =>  1  +  σφ²θ  = 1/ημ²θ  =>  ημ²θ = 1 / (1 + σφ²θ) = 1 / (1 + m₂ / m₁) =  m₁ / (m₁+ m₂)

  l₁ συνθ  +  l₂ ημθ  =   l₁  √[ m₂ / (m₁+ m₂) ]  +  l₂  √[ m₁ / (m₁+ m₂) ]  =  ( l₁  √m₂  +  l₂  √m₁ ) / √(m₁+ m₂)   (β)

ΘΕΜΑ Β
Β1. Σωληνοειδές (Σ) έχει αριθμό σπειρών ανά μονάδα μήκους n = 20 σπείρες/m και είναι φτιαγμένο από ομογενές κυλινδρικό σύρμα που έχει σταθερή διατομή ακτίνας r_Σ. Το σωληνοειδές έχει ωμική αντίσταση R_Σ και μέσω αγωγών αμελητέας αντίστασης συνδέεται με πηγή ΗΕΔ E και εσωτερικής
αντίστασης r_εσ  = R_Σ . Το μέτρο της έντασης του μαγνητικού πεδίου στο άκρο του σωληνοειδούς ισούται με B₁.
Αποσυνδέουμε το σωληνοειδές από την ηλεκτρική πηγή, το λιώνουμε και με όλο το υλικό του φτιάχνουμε ομογενές κυλινδρικό σύρμα που έχει σταθερή διατομή ακτίνας r_K .
Ψύχοντας το σύρμα στην ίδια θερμοκρασία στην οποία ήταν το σωληνοειδές (Σ) αποκτά ωμική αντίσταση R_K . Με το νέο σύρμα φτιάχνουμε κυκλικό αγωγό (Κ) ακτίνας  α_K = 5 cm, τον οποίο μέσω αγωγών αμελητέας αντίστασης συνδέουμε με την ίδια ηλεκτρική πηγή, στην οποία είχαμε συνδέσει το σωληνοειδές. Παρατηρούμε ότι το μέτρο της έντασης του μαγνητικού πεδίου B₂ στο κέντρο του κυκλικού αγωγού ισούται με το B₁.  Ο λόγος  r_Σ / r_Κ  ισούται με:
i. 1           ii. 2           iii. 4             iv. 8

  Ι₁  =  Ε / 2R_Σ      Β₁  =  4π 10^-7  20  Ι₁  =   4π 10^-7  20  Ε / 2R_Σ =   40π 10^-7  Ε / R_Σ         0γκος  =  L π r_Σ²  

  L = 2π α_κ  =  2π 0,05 = 0,1 π m         συνεχίζεται

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΕΜΑ Γ
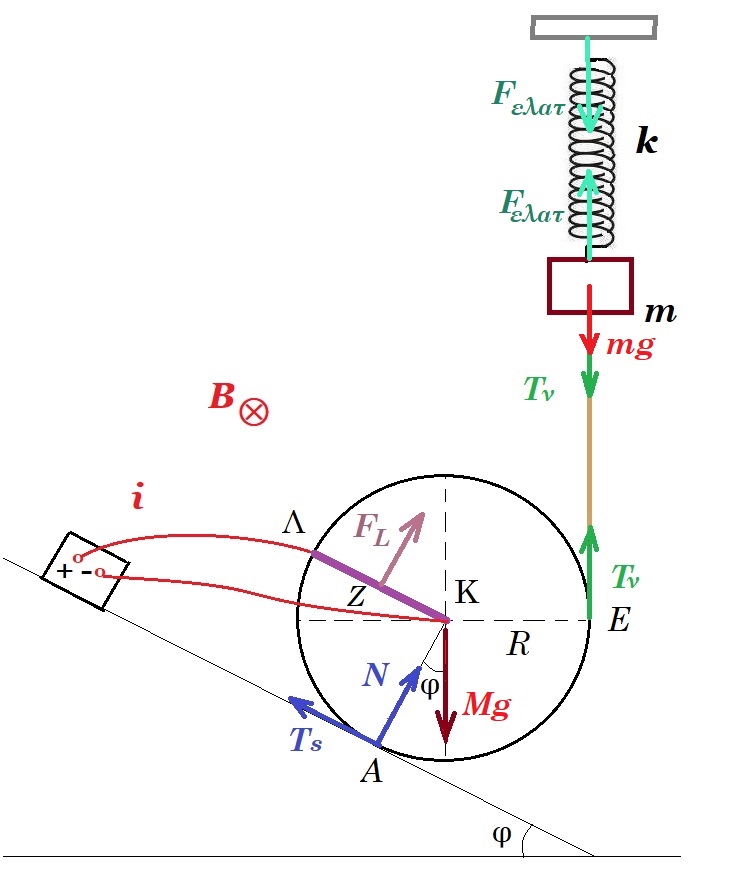
Ο ομογενής κύλινδρος του σχήματος έχει μάζα M=4kg, ακτίνα R=0,2m και είναι κατασκευασμένος από μονωτικά υλικά. Ο κύλινδρος έχει ενσωματωμένη μια αβαρή αγώγιμη ράβδο ΚΛ μήκους d=R που είναι παράλληλη στο κεκλιμένο επίπεδο γωνίας κλίσης φ, για την οποία ισχύει ότι ημφ=0,6 και συνφ=0,8. Η ράβδος τροφοδοτείται με ρεύμα έντασης Ι=4Α και βρίσκεται μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης Β=10Τ.  Ο κύλινδρος συνδέεται μέσω κατακόρυφου αβαρούς και μη εκτατού νήματος με σώμα μάζας m=0,25kg το οποίο είναι δεμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου με σταθερά k=100Ν/m, που το πάνω άκρο του είναι ακλόνητα στερεωμένο. Το σύστημα των σωμάτων ισορροπεί ακίνητο.
Γ1.  H στατική τριβή που ασκείται στον κύλινδρο έχει:
         α.  μέτρο 13,5 Ν και φορά προς τα πάνω                 β.  μέτρο 3 Ν και φορά προς τα πάνω
         γ.  μέτρο 13,5 Ν και φορά προς τα κάτω                  δ.  μέτρο 3 Ν και φορά προς τα κάτω
Τη χρονική στιγμή t = 0 το νήμα κόβεται  και  ταυτόχρονα η φορά του ρεύματος αντιστρέφεται και η τιμή της έντασής του διαμορφώνεται έτσι ώστε ο κύλινδρος να εξακολουθεί να ισορροπεί.
Γ2.  Η εξίσωση απομάκρυνσης y(t) της AAΤ που θα εκτελέσει το σώμα μάζας m μετά το κόψιμο του νήματος, θεωρώντας θετική φορά προς τα πάνω, είναι (στο S.I.):
α.  y  =  0,125  ημ(20t + 3π/2)         β.  y  =  0,175  ημ(10t + 3π/2)       

γ.  y  =  0,175  ημ(20t + 3π/2)         δ.  y  =  0,125  ημ(20t + π/2)
Γ3.  Η νέα τιμή της έντασης του ρεύματος είναι : 

α.    26 A              β.   25 A             γ.    24 A            δ.   23 A

Γ4.  Η ελάχιστη τιμή του συντελεστή οριακής τριβής που θα πρέπει να εμφανίζει ο κύλινδρος με το κεκλιμένο επίπεδο είναι:

α.    0,5                 β.   0,6               γ.    0,4              δ.  0,3       
Κάποια χρονική στιγμή το ρεύμα μηδενίζεται και ο κύλινδρος αρχίζει να κυλιέται χωρίς να ολισθαίνει. Μετά από χρονικό διάστημα Δt = √(3π/20) s  από τη στιγμή που ξεκίνησε, μια ακτίνα του διέγραψε γωνία 3π/2 rad. 
Γ5.  Το μέτρο της ταχύτητας του μέσου της ράβδου ΚΛ στο τέλος του χρονικού διαστήματος Δt είναι:
α.  2 m/s              β.  √(3π/5) m/s           γ.  √(4π/5) m/s          δ.  √3 m/s

Γ1.   η ράβδος διαρρέεται από ρεύμα μέσα σε μαγνητικό πεδίο :       F_L = Bid = 10 4 0,2 = 8 N

 ισορροπία κυλίνδρου

 Στ_(Α) = 0 :  Τ_ν (R + Rημφ)  -  Mg Rημφ - F_L R/2  =  0  =>  Τ_ν (1 + 0,6)  -  40 0,6 -  8 1/2  =  0  =>  Τ_ν = 17,5 N

 Στ_(Κ) = 0 : Τ_ν R  -  F_L R/2  -  T_s R  =  0 =>  17,5   -  8 1/2  -  T_s   =  0  =>  T_s = 13,5 N   και φορά προς τα πάνω  (a)

Γ2.   ισορροπία σώματος :  F_ελατ  -  mg  -  Τ_ν  =  0  =>   k x₀  -  mg  -  Τ_ν  =  0  =>  100 x₀  -  2,5  -  17,5  =  0  =>  x₀  =  0,2 m   επιμήκυνση

 ισορροπία σώματος χωρίς το νήμα :  F_ελατ  -  mg  =  0  =>  k x_!  =  mg  =>   100 x₁  =  2,5   => x₁  =  0,025 m   επιμήκυνση

 το σώμα θα εκτελέσει Α.Α.Τ.  με πλάτος  Α = 0,2 - 0,025 = 0,175 m  και

                   κυκλική συχνότητα  ω = (k / m)^½ =  (100 / 0,25)^½ = 20 rad/s  

     η αρχική φάση είναι  3π/2 rad            y(t)  =  0,175 ημ(20t + 3π/2)       (γ)

y(t)  =  0,175 ημ(20t + 3π/2)        v(t)  =  3,5 συν(20t + 3π/2)            a(t)  =  - 70  ημ(20t + 3π/2)

ΣF = m a  =>  F_ελατ  -  mg  =  m a  =>  F_ελατ(t)  =  2,5  -   0,25 70 ημ(20t + 3π/2)   => 

   =>  F_ελατ(t)  =  2,5  -  17,5 ημ(20t + 3π/2)       ή        F_ελατ(y)  =  2,5 - 100y     - 0,175 m £  y  £  + 0,175 m

U_ταλ  = ½ k y²  =  50 y²       - 0,175 m £  y  £  + 0,175 m              

U_ταλ  =  50 y²  =  50  0,175² ημ²(20t + 3π/2)  =  1,53125 ημ²(20t + 3π/2)

Κ  =  ½ m v²  =   ½  0,25  3,5² συν²(20t + 3π/2)  =  1,53125 συν²(20t + 3π/2)   

U_ελατ  =  ½ k (y - 0,025)²  =  50 (y - 0,025)²       - 0,175 m £  y  £  + 0,175 m   

U_ελατ  =  50 (y - 0,025)²   =  50 [ 0,175 ημ(20t + 3π/2)  -  0,025 ]²   

dK/dt  =  m v a =  0,25  3,5 συν(20t + 3π/2)  [ - 70  ημ(20t + 3π/2) ]  =  - 61,25  ημ(20t + 3π/2)  συν(20t + 3π/2) 

dU/dt = k y v  =  100   0,175 ημ(20t + 3π/2)   3,5 συν(20t + 3π/2)  =  61,25  ημ(20t + 3π/2)  συν(20t + 3π/2) 

Γ3.  ισορροπία κυλίνδρου

 Στ_(Α) = 0 :  F_L R/2  -  Mg Rημφ  =  0  =>   Bid R/2  -  Mg Rημφ  =  0  =>  10 i 0,2 1/2  =  40 0,6  =>  i = 24 Α   (γ)      F_L = Bid = 10 24 0,2 = 48 Ν

Γ4.  ροπές ως προς Κ :  F_L R/2  -  T_s R  =  0 =>  48 1/2  -  T_s   =  0  =>  T_s = 24 N   και φορά προς τα πάνω     

ΣF_y = 0 => N  - F_L  - Mg συνφ =  0  => N  -  48 -  40 0,8 = 0  => N = 80 N

 Τ_s = μ Ν =>  24 = μ 80 =>  μ = 0,3      (δ)        

Γ5.    θ  =  ½  α_γων  t²  =>  3π/2  =  ½  α_γων  3π/20  => α_γων = 20 rad/s²            ω  =  α_γων  t  =  20 √(3π/20) rad/s  

  v_cm  =  ω R  =  20 √(3π/20) rad/s   0,2 m  = 4 √(3π/20) m/s               

  v_Z  =  ω R  -  ω R/2  = ω R/2  = 2 √(3π/20) m/s = √(3π/5) m/s