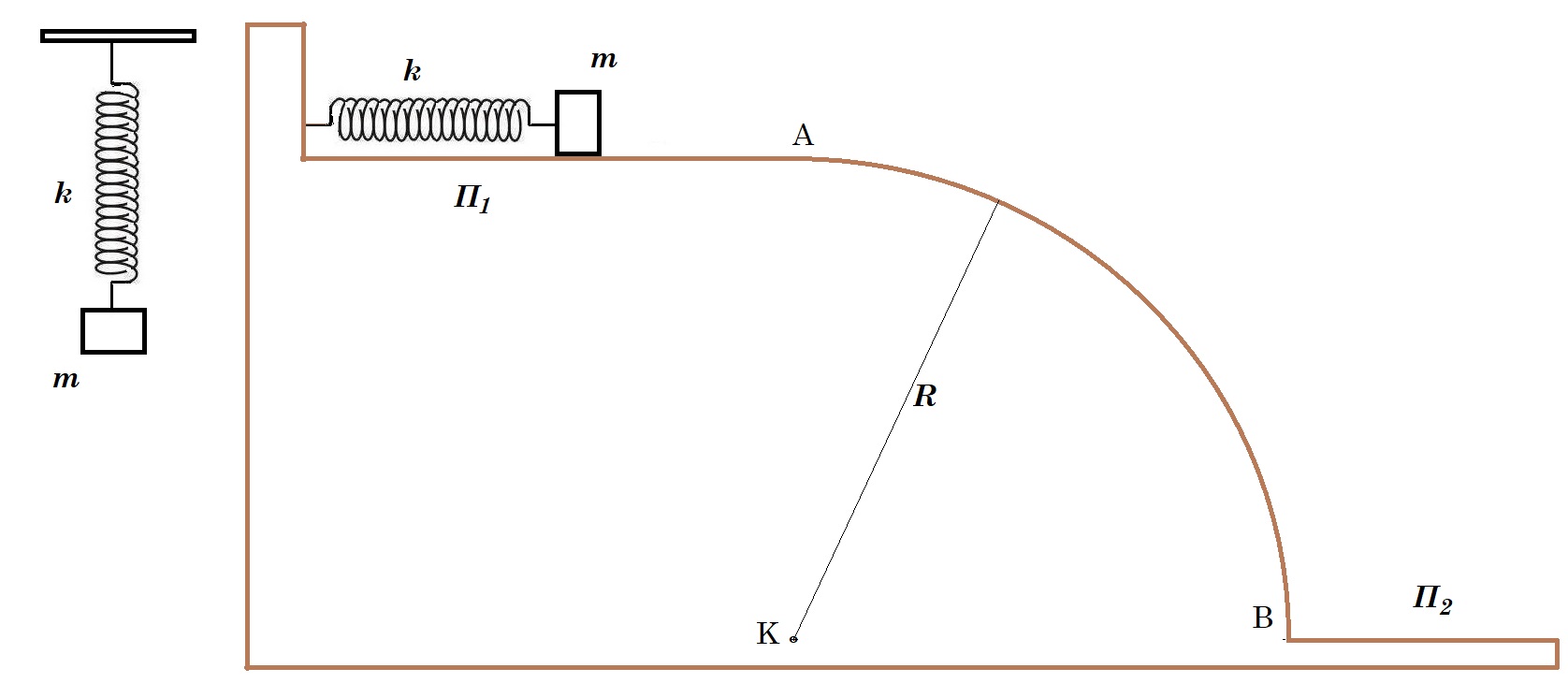
Α1.  Όταν ένα σώμα ισορροπεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k , που το πάνω άκρο του είναι στερεωμένο σε ακλόνητο σημείο, η επιμήκυνσή του είναι  Δl.  Τοποθετούμε το σύστημα ελατήριο-σώμα σε λείο οριζόντιο επίπεδο (Π₁)  και το σώμα εκτελεί απλή αρμονική ταλάντωση πλάτους Α με σταθερά επαναφοράς D = k.  Κάποια στιγμή καθώς το σώμα διέρχεται από τη θέση φυσικού μήκους του ελατηρίου, αποκολλάται από το ελατήριο και συνεχίζει να κινείται στο οριζόντιο επίπεδο.  Στη συνέχεια εισέρχεται στην κυρτή επιφάνεια λείου τεταρτοκυκλίου ακτίνας R και χάνει την επαφή του με αυτό σε ύψος
h από το οριζόντιο δάπεδο (Π₂).  Ισχύει η σχέση:

α.   h = ( A² + 3RΔl ) / 3Δl            β.   h = ( A² + 2RΔl ) / 3Δl              

γ.   h = ( A² + RΔl ) / 3Δl              δ.   h = ( 3A² + RΔl ) / 3Δl         

  ισορροπία ελατηρίου - σώματος :  k Δl  =  m g    (1)

το σώμα εκτελεί Α.Α.Τ. επάνω στο λείο οριζόντιο επίπεδο Π₁ :  ½ k A² =  ½ m v₀²  =>  v₀² = kA²/m  =⁽¹⁾ gA²/Δl   (2)

το σώμα είναι στο σημείο Γ  σε ύψος h από το οριζόντιο επίπεδο Π₂  τότε έχει ταχύτητα υ  και η επιβατική ακτίνα σχηματίζει με την κατακόρυφο γωνία θ   h = R συνθ    (3)     

διατήρηση ενέργειας από (Α) σε (Γ) :   ½ m v₀²  +  mg (R - h)  =  ½ m v²  =>  v₀²  +  2g (R - h)   =  v²   (4)

το σώμα κινείται στο λείο τεταρτοκύκλιο :  ΣF_y  =  F_K  =>  mg συνθ  -  Ν  =  m v² / R  χάνει την επαφή όταν Ν = 0  τότε :   mg συνθ  =  m v² / R  =>  v² =  Rg συνθ  = g h   (5)

(4) =>   v₀²  +  2g (R - h)  =  v²  =>  gA²/Δl  +  2g (R - h)  =  Rg συνθ  =>  gA²/Δl  +  2g (R - h)  =  g h  =>

        =>   A²/Δl  +  2R -  2h  =  h   =>   A²/Δl  +  2R  =  3h   (β)

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

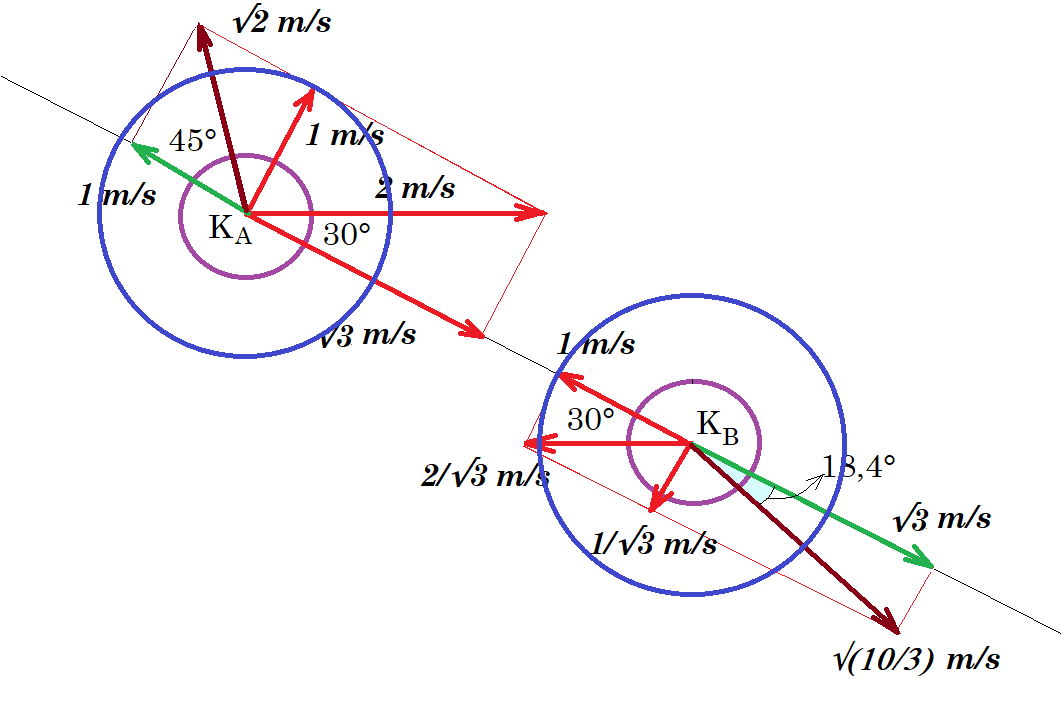
Β1.  Δύο όμοιοι λείοι επίπεδοι δίσκοι (Α) και (Β) κινούνται στο ίδιο οριζόντιο επίπεδο ο ένας προς τον άλλο, έτσι ώστε οι ταχύτητες τους  υ_Α  και  υ_B  αντίστοιχα, να έχουν διευθύνσεις παράλληλες στον οριζόντιο άξονα xx'.  Οι ταχύτητες έχουν μέτρα  υ_Α = 2 m/s   και  υ_Β = 2^.√3/3 m/s.  Οι δίσκοι
συγκρούονται ελαστικά και τη στιγμή της κρούσης η ευθεία που συνδέει τα κέντρα τους σχηματίζει με τον άξονα xx'  γωνία 150°.  Να υπολογίσετε τη γωνία που θα σχηματίζει η ταχύτητα του
δίσκου (Α) με τον άξονα xx'  μετά την κρούση.

  διατήρηση ορμής άξονας K_AK_B :  m v_A συν30°  -  m v_Β συν30°  =  m v_A' συνθ_Α  +  m v_Β' συνθ_Β  =>

          =>   2 √3/2  -  2√3/3 √3/2   =  v_A' συνθ_Α  +  v_Β' συνθ_Β   =>  √3  -  1  =  v_A' συνθ_Α  +  v_Β' συνθ_Β   (1)

 διατήρηση ενέργειας : 

  ½ m ( v_A συν30° )²  +  ½ m  ( v_Β συν30° )²  =  ½ m ( v_A' συνθ_Α )²  +  ½ m ( v_Β' συνθ_Β )²    =>  

=>   √3²   +   1²  =    ( v_A' συνθ_Α )²  +   ( v_Β' συνθ_Β )²   =>    4  =   ( v_A' συνθ_Α )²  +   ( v_Β' συνθ_Β )²   (2)   

(2) , (1) =>    4  =   ( v_A' συνθ_Α )²  +   ( √3 - 1 -  v_Α' συνθ_Α )²  => 

       =>    4  =   ( v_A' συνθ_Α )²  +   (√3 - 1)²  +   (v_Α' συνθ_Α)²  -  2 (√3 - 1)  v_Α' συνθ_Α   => 

       =>    4  =   2 (v_A' συνθ_Α)²  +   4  -  2√3  -  2 (√3 - 1)  v_Α' συνθ_Α   => 

       =>    0  =   (v_A' συνθ_Α)²  -  (√3 - 1)  v_Α' συνθ_Α   -  √3               Δ =  (√3 - 1)²   +  4 √3  =  (√3 + 1)²        

  v_A' συνθ_Α  =  (- β ± √Δ) / 2α  =   [ (√3 - 1)  ±   (√3 + 1) ] / 2  =   √3 m/s  αρχική ταχύτητα άρα απορρίπτεται   ή  

  v_Α' συνθ_Α  =  - 1 m/s  δεκτή λύση        οπότε   v_Β' συνθ_Β  =  √3 - 1 -  v_Α' συνθ_Α =  √3 - 1 -  1  = √3 m/s   

  δεν ασκούνται δυνάμεις στον κάθετο άξονα  Κ_ΑΚ_Β  οπότε οι συνιστώσες των ταχυτήτων περαμένουν οι ίδιες

          v_A ημ30°  =  v_A' ημθ_Α =  1 m/s                                  -  v_Β ημ30°  =  v_Β' ημθ_Β   =  - √3/3 m/s

  v_A'² συν²θ_Α  +   v_A'² ημ²θ_Α   =   v_A'²  =   1 + 1 = 2  =>  v_A' = √2 m/s         

         εφθ_Α  =  1 / (- 1)  =  - 1   => θ_Α = - 45°  =  900°  +  45°  =   135°   

  v_Β'² συν²θ_Β   +   v_Β'² ημ²θ_Β   =  v_Β'²   =   (√3)²  +  (√3/3)²  =  3  +  1/3  =  10/3  =>  v_B'  = √10/3 m/s       

         εφθ_Β  = ( - √3/3 ) / √3  =  - 1/3  =>  θ_Β =  - 18,4°

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

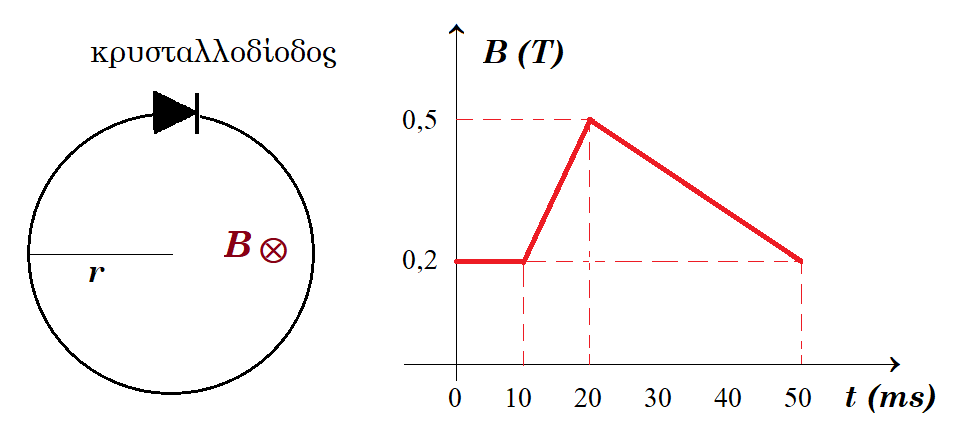
Η κρυσταλλοδίοδος είναι μία διάταξη η οποία επιτρέπει τη διέλευση του ηλεκτρικού ρεύματος μόνο κατά τη μία φορά (ορθή φορά).  Εάν το ηλεκτρικό ρεύμα έχει αντίθετη φορά από την ορθή, τότε η κρυσταλλοδίοδος δεν επιτρέπει τη διέλευσή του και το ρεύμα μηδενίζεται.   Κυκλικός αγωγός ακτίνας r = π^-½ m  και ωμικής αντίστασης R =10 Ω  βρίσκεται σε οριζόντιο επίπεδο, μέσα σε ομογενές
μαγνητικό πεδίο έντασης μέτρου Β, οι δυναμικές γραμμές του οποίου είναι κατακόρυφες με φορά από τον αναγνώστη προς τη σελίδα.  Στον κυκλικό αγωγό υπάρχει κρυσταλλοδίοδος, όπως φαίνεται στο σχήμα. Το μέτρο της έντασης Β μεταβάλλεται με το χρόνο t, όπως φαίνεται στη γραφική παράσταση.
Η θερμότητα Q που εκλύεται στον κυκλικό αγωγό στη διάρκεια των 50 ms ισούται με:
α. 0            β. 0,3 J               γ. 0,9 J             δ. 1, 2 J

από  0s έως 10s η ένταση Β του μαγνητικού πεδίου είναι σταθερή οπότε δεν εμφανίζεται επαγωγική τάση στον κυκλικό αγωγό  

από 10s  έως 20s  η ένταση Β αυξάνεται προς τα μέσα με συνέπεια να εμφανισθεί επαγωγική τάση έτσι ώστε το επαγωγικό ρεύμα να έχει τέτοια φορά που να δημιουργεί μαγνητικό πεδίο τέτοιο ώστε να μειώνει το υπάρχον μαγνητικό πεδίο  η φορά του επαγωγικού ρεύματος είναι αριστερόστροφη ( αντίθετη της κίνησης των δεικτών του ρολογιού )  αλλά η κρυσταλλοδίοδος δεν επιτρέπει την διέλευσή του

από 20s  έως 30s  η ένταση Β  μειώνεται προς τα μέσα με συνέπεια να εμφανισθεί επαγωγική τάση έτσι ώστε το επαγωγικό ρεύμα να έχει τέτοια φορά που να δημιουργεί μαγνητικό πεδίο τέτοιο ώστε να αυξάνει το υπάρχον μαγνητικό πεδίο  η φορά του επαγωγικού ρεύματος είναι δεξιόστροφη ( ίδια με την κίνηση των δεικτών του ρολογιού )   η κρυσταλλοδίοδος  επιτρέπει την διέλευσή του

  Ε_επαγ = - ΔΦ / Δt =  - A  ΔB / Δt = - π r²  ΔB / Δt  =  -  π/π  (0,2  - 0,5)/ (0,05 - 0,02)  =  10 Volt 

  i = Ε_επαγ / R = 10 / 10 = 1 A             Q = i² R t =  1² 10  0,03  =  0,3 J       (β)                

ΘΕΜΑ Γ
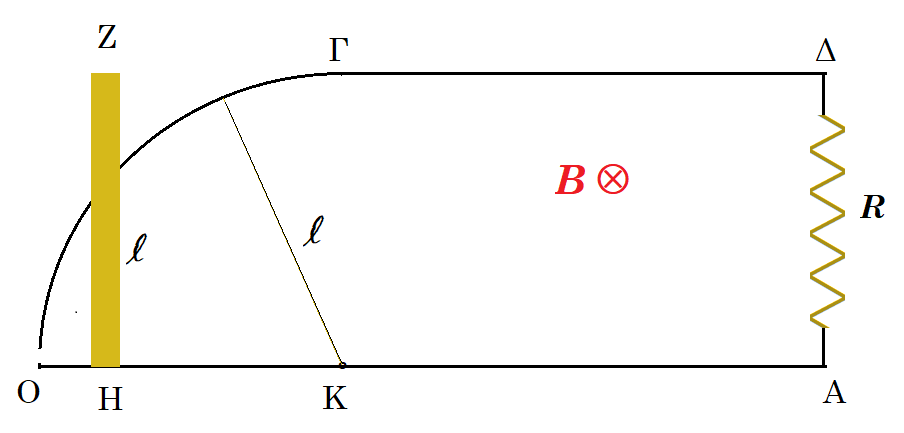
Δίνεται η διάταξη του σχήματος, η οποία βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο έντασης μέτρου B = 2 T, με διεύθυνση κάθετη στο οριζόντιο επίπεδο (Π) του σχήματος, με φορά από τον αναγνώστη προς το επίπεδο (Π). Η διάταξη αποτελείται από:
• τον αγωγό ΟΓ σχήματος τεταρτοκυκλίου ακτίνας  l =1 m αμελητέας ωμικής αντίστασης
• τον ευθύγραμμο αγωγό ΟΑ αμελητέας ωμικής αντίστασης

• τον ευθύγραμμο αγωγό ΓΔ αμελητέας ωμικής αντίστασης είναι παράλληλος προς τον ΟΑ και απέχει απόσταση  l =1 m από αυτόν.  Τα άκρα Α και Δ των αγωγών ΓΔ και ΟΑ συνδέονται αγώγιμα μέσω αντιστάτη  που έχει αντίσταση R = π/2  Ω.    Οι αγωγοί ΟΓ και ΟΑ δεν συνδέονται στο σημείο Ο. Ομογενής μικρού πάχους αγώγιμη ράβδος ΗΖ ωμικής αντίστασης R₁ = π/2 Ω  και μήκους l = (ΗΖ) = 1m κινείται στο επίπεδο (Π) παράλληλα στον εαυτό της, μένοντας πάντοτε κάθετη στον αγωγό ΟΑ. Το άκρο της Η είναι πάντοτε σε επαφή με τον αγωγό ΟΑ.  Η ράβδος είναι επίσης κατά την κίνησή της συνεχώς σε επαφή με τον αγωγό ΟΓ ή τον αγωγό ΓΔ.  Αρχικά η ράβδος είναι ακίνητη, έτσι ώστε το άκρο της Η να βρίσκεται στο σημείο Ο. Τη χρονική στιγμή t_o = 0  ασκούμε δύναμη F στο μέσο της ράβδου με διεύθυνση παράλληλη της ΟΑ, οπότε αρχίζει να κινείται με τέτοιο τρόπο, ώστε το
σημείο επαφής της με τον αγωγό ΟΓ να έχει σταθερή γωνιακή ταχύτητα μέτρου  ω = π/2 rad/s. Η ράβδος φτάνει στο σημείο Γ τη χρονική στιγμή t₁  με ταχύτητα  υ₁  και με την ταχύτητα αυτή συνεχίζει να κινείται, έως ότου φτάσει στα σημεία Α και Δ.

Γ1.  Εκφράστε την επαγωγική τάση που εμφανίζεται στον αγωγό κατά την διάρκεια της κίνησής του από τη χρονική στιγμή t_o = 0  μέχρι να φθάσει στο σημείο Γ τη χρονική στιγμή t₁.

Γ2.  Αν η θερμότητα που εκλύεται κατά την κίνηση της ράβδου ΗΖ, όταν είναι σε επαφή με τον αγωγό ΓΔ, ισούται με Q = 2 J , να υπολογίσετε το μήκος (ΓΔ).

Γ3.  Τη χρονική στιγμή   t₂ = 1/3 s, να υπολογίσετε την τάση από επαγωγή στο τμήμα της ράβδου που διαρρέεται από ηλεκτρικό ρεύμα.

Γ4.  Τη χρονική στιγμή  t₂ = 1/3 s, να υπολογίσετε την ένταση του ηλεκτρικού ρεύματος που διαρρέει το κύκλωμα, καθώς και την ισχύ της δύναμης Laplace.

 Γ1.   υ = ω l  =  π/2  1  =  π/2 m/s             Ε_επαγ = Β  υ ημθ  (ΜΗ) =  Β  υ ημθ  l ημθ  =   2  π/2  ημ²θ  =  π ημ²θ 

 Γ2.     όταν φθάνει στο σημείο Γ  η γωνία  θ = 90°  οπότε   v₁  = π/2 m/s   και   Ε_επαγ  = π Volt     από εκεί μέχρι το σημείο Δ  εφαρμόζουμε νόμο του Οhm :   Ε_επαγ  = i ( R + R₁ )  =>  π  =  i  ( π/2 + π/2 ) =>  i  =  1 Α

  Q  =  i²  ( R + R₁ )  t  =  i²  ( R + R₁ )  x / v₁  =>   2 J  =  1 A²  π Ω   x / π/2 m/s  =>  x  =  1 m  =  (ΓΔ)

 Γ3.    τη στιγμή t₂ = 1/3 s   η γωνία  θ  =  ω t₂  =  π/2  1/3  =  π/6  =  30°        E_επαγ  =  π ημ²30°  =  π/4 Volt  

  η ράβδος έχει διανύσει διάστημα  υ ημθ t₂  =  π/2  ημ30°  1/3  =  π/12 m 

 Γ4.     Ε_επαγ  = i ( R + R₁ ημθ )  =>  π/4  =  i  ( π/2 + π/2 ημ30° ) =>  π/4  =  i  ( π/2 + π/4 )  => i  =  1/3 Α

   P_FL  =   B  i  (MH)  υ ημθ   =  B  i  l ημθ  υ ημθ  =   2  1/3  1  π/2  ημ²30°  =  π/12 J/s    απώλεια ισχύος 

Γ5.     Ε_επαγ  = i ( R + R₁ ημθ )  =>   π ημ²θ  =  i  ( π/2 + π/2 ημθ )  =>   i  =  π ημ²θ / π/2 (1 + ημθ)  =>

                     =>   i  =  2 ημ²θ / (1 + ημθ)