(1)

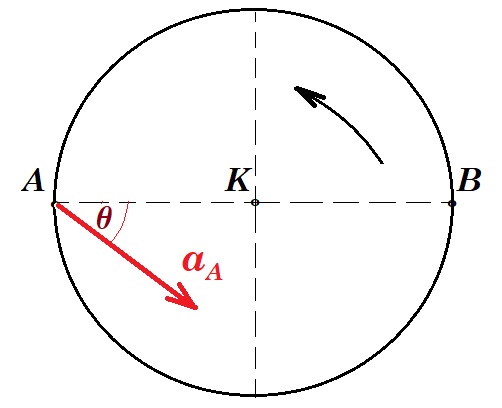
Ένας ομογενής οριζόντιος δίσκος ακτίνας R=1m, κινείται σε λείο οριζόντιο επίπεδο με την επίδραση κατάλληλης δύναμης F. Κάποια στιγμή που ο δίσκος έχει γωνιακή ταχύτητα ω=1rad/s και γωνιακή επιτάχυνση αγων=3rad/s2, διανύσματα κατακόρυφης διεύθυνσης με φορά προς τα πάνω, το σημείο Α στο άκρο μιας ακτίνας στη διεύθυνση x, έχει επιτάχυνση μέτρου αΑ=5m/s2 η οποία σχηματίζει γωνία θ (ημθ=0,6) με την ακτίνα, όπως στο σχήμα. Να υπολογιστούν:
1) η επιτάχυνση του κέντρου μάζας Κ του δίσκου
2) η επιτάχυνση του αντιδιαμετρικού σημείου Β του δίσκου.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(2)
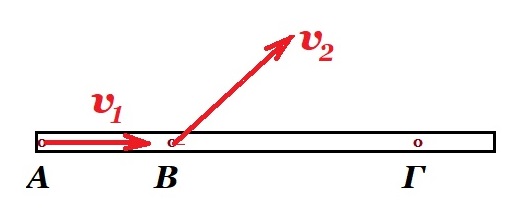
Μια ράβδος κινείται οριζόντια σε λείο οριζόντιο επίπεδο. Κάποια στιγµή το άκρο Α, έχει ταχύτητα µέτρου υ1=1m/s, όπως στο σχήµα. Την ίδια στιγµή το σηµείο Β, το οποίο απέχει από το Α κατά
(ΑΒ)=1m, έχει ταχύτητα υ2 η οποία σχηµατίζει γωνία 45° µε τον άξονα της ράβδου.
Να βρεθεί η ταχύτητα, τη στιγµή αυτή, του σηµείου Γ, αν (ΑΓ)=3m;
(1)
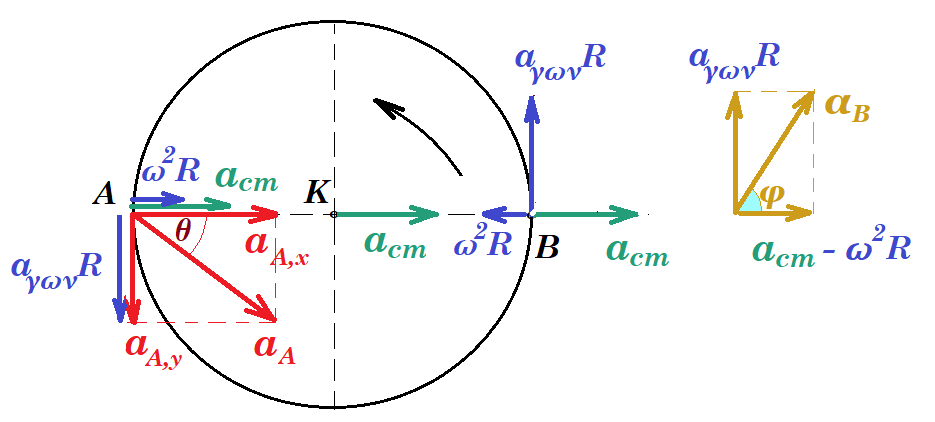
η επιτάχυνση του σημείου Α αναλύεται σε μια συνιστώσα κατά το άξονα ΑΚ : aA,x = aA συνθ = 5m/s2 0,8 = 4m/s2 και μια συνιστώσα κάθετη στον άξονα ΑΚ : aA,y = aA ημθ = 5m/s2 0,6 = 3m/s2
ο δίσκος εκτελεί μεταφορική κίνηση και περιστροφική περί το κέντρο μάζας του Κ
το σημείο Α έχει επιτρόχια επιτάχυνση aA,y = 3m/s2 κεντρομόλο επιτάχυνση ακ = ω2 R = (1rad/s)2 1m = 1m/s2 και μεταφορική επιτάχυνση acm του κέντρου μάζας Κ του δίσκου , η κεντρομόλος ακ και η μεταφορική acm του κέντρου μάζας είναι κατά τον άξονα ΑΚ ομόρροπες συνεπώς ακ + acm = aA,x => 1m/s2 + acm = 4m/s2 => acm =3m/s2 δηλαδή το κέντρο μάζας Κ του δίσκου έχει επιτάχυνση acm = 3 m/s2
το σημείο Β έχει επιτρόχια επιτάχυνση με μέτρο aΒ,y = 3m/s2 κεντρομόλο επιτάχυνση ακ = ω2 R = (1rad/s)2 1m = 1m/s2 και μεταφορική επιτάχυνση acm = 4m/s2 του κέντρου μάζας Κτου δίσκου , η κεντρομόλος ακ και η μεταφορική acm του κέντρου μάζας είναι κατά τον άξονα ΑΚ αλλά αντίρροπες συνεπώς aB,x = ακ + acm => -1m/s2 + 3m/s2 => aB,x = 2m/s2 aB2 = aB,x2 + aB,y2 = 22 + 32 = 13 => aB = √13 m/s2
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
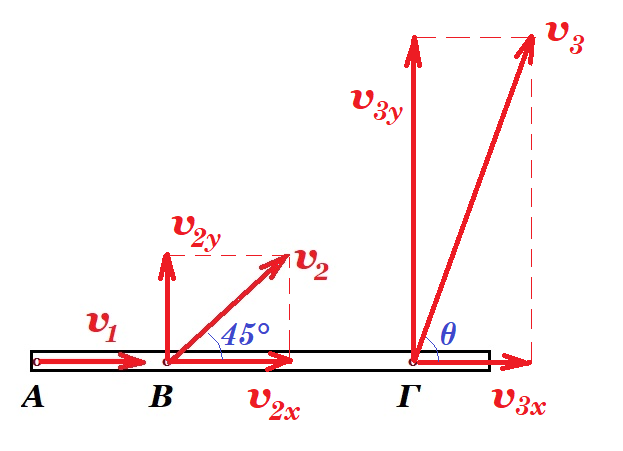
(2) η ταχύτητα v2 του σημείου Β της ράβδου σχηματίζει με τον άξονά της γωνία 45° που αναλύεται σε μια συνιστώσα v2x κατά τον άξονα και μια συνιστώσα v2y κάθετη στον άξονα έχουμε v2x = v2y
συμπεραίνουμε ότι η ράβδο και μεταφέρεται και περιστρέφεται
το σημείο Α έχει ταχύτητα v1 κατά τον άξονα της ράβδου εκτελεί μεταφορική κίνηση
η ράβδος περιστρέφεται περί το άκρο της Α με γωνιακή ταχύτητα ω έτσι v2y = ω (ΑΒ) και v2x = v1 = 1m/s άρα v2y = ω (ΑΒ) = v2x = v1 = 1 m/s οπότε v2 = √2 m/s
το σημείο Γ έχει συνιστώσα κατά τον άξονα v3x = v1 = 1 m/s και συνιστώσα κάθετη στον άξονα v3y = ω (ΑΓ) = ω 3 (ΑΒ) = 3 m/s συνεπώς v32 = v3x2 + v3y2 = 12 + 32 = 10 => v3 = √10 m/s εφθ = v3y / v3x = 3