(1)

Ένας τροχός ακτίνας R=0,6m ηρεμεί σε οριζόντιο επίπεδο. Τη στιγμή tο=0 τίθεται σε κίνηση αποκτώντας επιτάχυνση κέντρου μάζας Κ αcm, η οποία μεταβάλλεται όπως στο πρώτο από τα παρακάτω διαγράμματα και γωνιακή επιτάχυνση, όπως στο δεύτερο διάγραμμα και με κατευθύνσεις όπως στο σχήμα. Να βρεθούν:
i)  Η ταχύτητα του κέντρου Κ του τροχού, καθώς και η γωνιακή ταχύτητα του τροχού την χρονική στιγμή t1=2s.
ii) Η ταχύτητα και η οριζόντια επιτάχυνση του σημείου επαφής του τροχού με το επίπεδο, σημείου Α, τις χρονικές στιγμές:   α) t1= 2s,     β) t3= 6s.

(2)

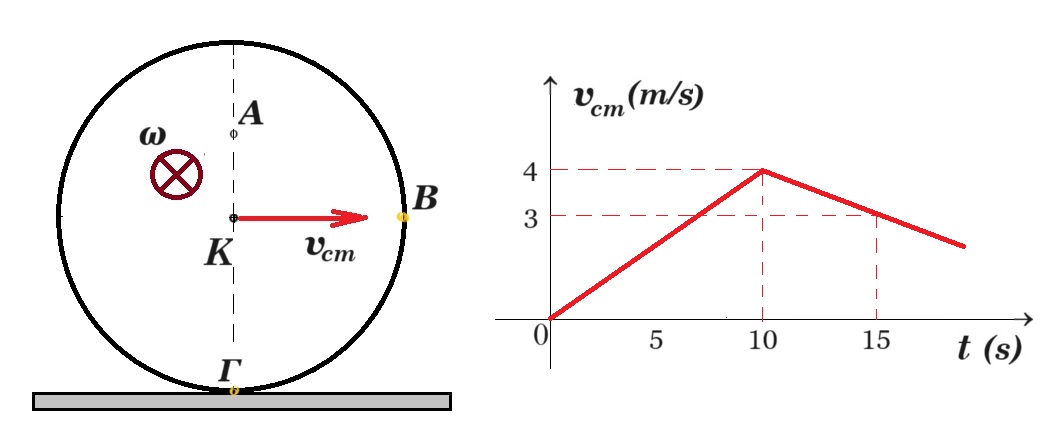Ένα αυτοκίνητο βρίσκεται ακίνητο σε οριζόντιο δρόμο. Κάποια στιγμή το αυτοκίνητο αρχίζει να κινείται ευθύγραμμα και στο διάγραμμα δίνεται η ταχύτητά του σε συνάρτηση με το χρόνο. Μελετάμε την κίνηση του τροχού του αυτοκινήτου, κέντρου (και κέντρου μάζας) Κ, με ακτίνα R=0,8m, ο οποίος διαρκώς κυλίεται (χωρίς να ολισθαίνει).

α)  Να βρεθεί η επιτάχυνση του κέντρου Κ καθώς και η γωνιακή επιτάχυνση του τροχού, την στιγμή t1=5s.
β) Να υπολογισθούν η ταχύτητα, η οριζόντια επιτάχυνση αx  και η κατακόρυφη επιτάχυνση αy του σημείου Α του τροχού, στο μέσον μιας κατακόρυφης ακτίνας, όπως στο σχήμα, την στιγμή t1.
γ) Ποιες οι αντίστοιχες απαντήσεις για το σημείο Β του τροχού, στο άκρο μιας οριζόντιας ακτίνας του, την χρονική στιγμή t2=15s;

 

 

(1)

 t1 = 2 s :    vcm = acm t = 2 m/s2 2 s = 4 m/s         ω = (8 + 4) rad/s2  2 s / 2 = 12 rad/s   

 t1 = 2 s :   vA =  vcm - ωR  =  4 m/s -  12 rad/s 0,6 m = - 3,2 m/s       

                aA =  acm -  aγων R  =  2 m/s2 -   4 rad/s2 0,6 m = - 0,4 m/s2       

 t2 = 4 s :    vcm = acm t = 2 m/s2 4 s = 8 m/s         ω = 8 rad/s2  4 s / 2 = 16 rad/s   

 t1 = 6 s :   vA =  vcm - ωR  =  acm t  -  ωR  =  2 m/s2 6 s  -  16 rad/s 0,6 m = 2,4 m/s       

                aA =  acm -  aγων R  =  2 m/s2  -   0  =  2 m/s2       

 

 

 

(2)

t1=5s    α = v / t = 4 m/s / 10 s = 0,4 m/s2              αγων = acm / R = 0,4 m/s2 / 0,8 m = 0,5 rad/s2  

 

t1=5s    vcm = 2 m/s      ω = vcm / R  =  2 m/s / 0,8 m  =  2,5 rad/s2   

          vA  =  vcm +  ω R/2  =  2 m/s + 2,5 rad/s2 0,4 m  =  3 m/s

       aA,x  =  acm  +  αγων R/2  =  1,5 acm  =  1,5  0,4 m/s2 =  0,6 m/s2   

       aA,y  =   ακ  =  ω2 R/2  =  2,52  0,4  = 2,5 m/s2  

 

t1=15s    vcm = 3 m/s      ω =  vcm / R  = 3 m/s / 0,8 m  =  3,75 rad/s2          

  acm =  (3 - 4) m/s / (15 - 10) s  =  - 0,2 m/s2                      ακ  =  ω2 R  =  3,752  0,8  =  11,25 m/s2  

     vB2  =  vcm2  +  (ω R)2  =  32 +  (3,75  0,8)2  =>  vB = 3√2 m/s            

  aB,x =  acm  +  ακ  =  - 0,2  +  (- 11,25 )  =  - 11,45 m/s2                aB,y =  αγων R   = acm =  0,2 m/s2