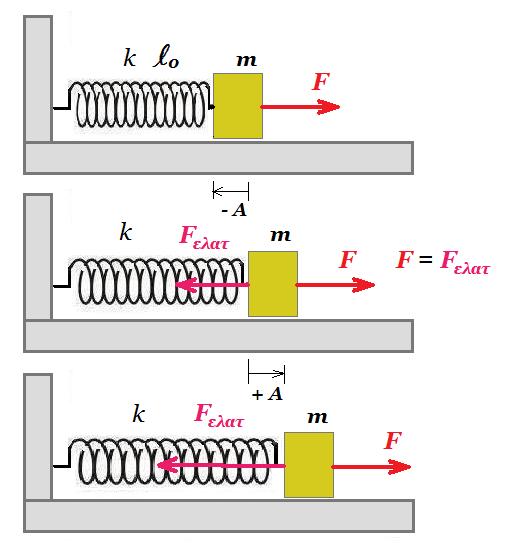
F = 75 + 250 x F = 0 => x = - 75 / 250 = - 0,3 m Fελατ = - k x = - 250 N/m (- 0,3 m) = 75 N
ΣF = F + Fελατ = 75 + 250 x - 250 x = 75 N σταθερή δύναμη άρα το σώμα θα εκτελεί ευθύγραμμη ομαλά επιταχυνόμενη κίνηση χωρίς αρχική ταχύτητα με επιτάχυνση α = ΣF / m = 75 N / 10 kg = 7,5 m/s2
το σώμα διανύει διάστημα x = 0,2 m σε χρόνο t
x = ½ a t2 => 0,2 m = ½ 7,5 m/s2 t2 => t2 = 4/75 = 4/25 1/3 = 0,16 / 3 => t = 0,4/√3 s
v = a t = 7,5 0,4/√3 = 0,75 4/√3 = 3/4 4/√3 = √3 m/s
K = ½ m v2 = ½ 10 3 = 15 J Uελατ = ½ k x2 = ½ 250 0,22 = 5 J 15 J + 5 J = 20 J
το μέτρο της δύναμης μεταβάλλεται από 75 Ν όταν x = 0 μέχρι 75 + 250 . 0,2 = 125 Ν όταν x = 0,2 m μετά η δύναμη καταργείται,
στο διάστημα ( 0 , 0,2 m ) η δύναμη παράγει έργο : WF = (75 + 125) N 0,2 m / 2 = 20 J
το έργο αυτό γίνεται ενέργεια της ταλάντωσης του σώματος : Ε = ½ k A2 => 20 J = ½ 250 N/m A2 => A=0,4m
ω2 = k / m = 250 / 10 => ω = 5 rad/s
x(t) = 0,4 ημ(5t + θ) x(0) = 0,4 ημθ = + 0,2 => ημθ = + 0,5 => θ = 30° = π/6 rad
x(t) = 0,4 ημ(5t + π/6) v(t) = 2 συν(5t + π/6) α(t) = - 10 ημ(5t + π/6)
η μέγιστη ταχύτητα του σώματος είναι v'max = ω Α = 5 rad/s 0,4 m = 2 m/s
οπότε έχουμε : v / v'max = √3 / 2 (α)
dK/dt = m v a = 10 2 συν(5t + π/6) [ - 10 ημ(5t + π/6) ] = - 200 ημ(5t + π/6) συν(5t + π/6)
dU/dt = k x v = 250 0,4 ημ(5t + π/6) 2 συν(5t + π/6) = + 200 ημ(5t + π/6) συν(5t + π/6)
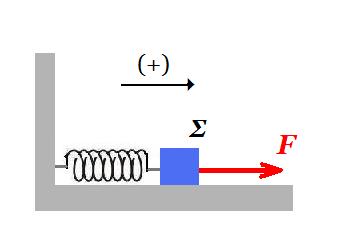 Το σώμα μάζας m = 10 kg ισορροπεί ακίνητο πάνω σε λείο οριζόντιο δάπεδο δεμένο στο ένα άκρο ιδανικού οριζοντίου ελατηρίου σταθεράς k = 250 N/m. Το άλλο άκρο του ελατηρίου είναι ακλόνητο. Ασκούμε στο σώμα δύναμη κατά τη διεύθυνση του άξονα του ελατηρίου έτσι ώστε το ελατήριο να επιμηκύνεται το μέτρο της δύναμης μεταβάλλεται με την επιμήκυνση του ελατηρίου σύμφωνα με τη σχέση F = 75 + 250x (SI). Η δύναμη F καταργείται όταν η επιμήκυνση του ελατηρίου γίνει x = 0,2 m. Ο λόγος υmax/υ′max όπου υmax η μέγιστη ταχύτητα του σώματος όταν ασκείται η δύναμη και υ′max η μέγιστη ταχύτητα του σώματος αφού καταργηθεί η δύναμη είναι: α. (√3)/2 β. 1/2 γ. 1
Το σώμα μάζας m = 10 kg ισορροπεί ακίνητο πάνω σε λείο οριζόντιο δάπεδο δεμένο στο ένα άκρο ιδανικού οριζοντίου ελατηρίου σταθεράς k = 250 N/m. Το άλλο άκρο του ελατηρίου είναι ακλόνητο. Ασκούμε στο σώμα δύναμη κατά τη διεύθυνση του άξονα του ελατηρίου έτσι ώστε το ελατήριο να επιμηκύνεται το μέτρο της δύναμης μεταβάλλεται με την επιμήκυνση του ελατηρίου σύμφωνα με τη σχέση F = 75 + 250x (SI). Η δύναμη F καταργείται όταν η επιμήκυνση του ελατηρίου γίνει x = 0,2 m. Ο λόγος υmax/υ′max όπου υmax η μέγιστη ταχύτητα του σώματος όταν ασκείται η δύναμη και υ′max η μέγιστη ταχύτητα του σώματος αφού καταργηθεί η δύναμη είναι: α. (√3)/2 β. 1/2 γ. 1