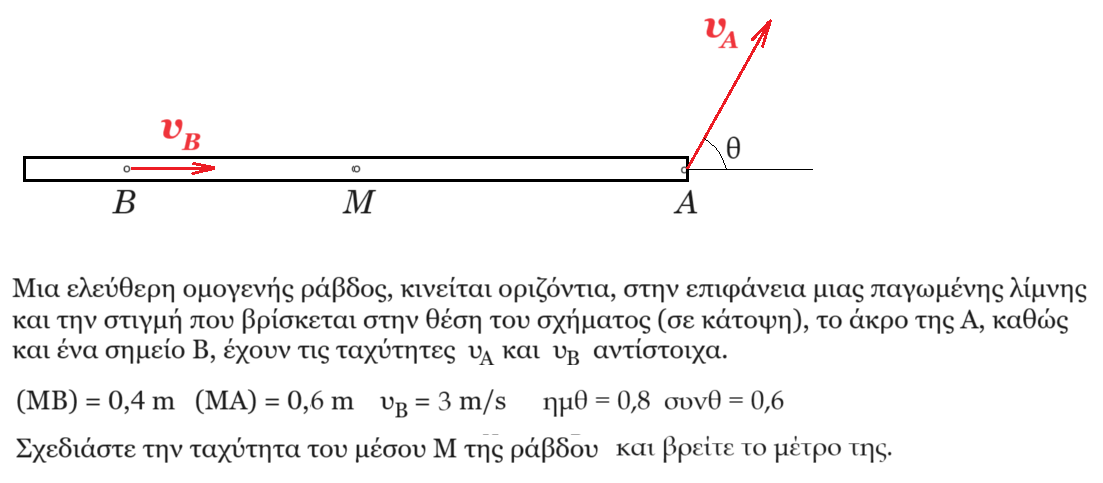
η ταχύτητα του σημείου Β μας δείχνει ότι η ράβδος εκτελεί μεταφορική κίνηση    οπότε όλα τα σημεία της ράβδου έχουν την ίδια ταχύτητα

η ταχύτητα υ_Α  αναλύεται σε δύο κάθετες συνιστώσες  v_A,x = v_A συνθ  η οποία ισούται με την ταχύτητα του σημείου Β  δηλαδή   v_A,x = v_A συνθ = v_B  =>   v_A  0,6 = 3 m/s  =>  v_A = 5 m/s   

η συνιστώσα  v_A,y = v_A  ημθ  =  5 m/s 0,8  =>  v_A,y = 4 m/s  μας δείχνει ότι η ράβδος στρέφεται περί άξονα κάθετο στην ράβδο που διέρχεται από το σημείο Β

το σημείο Μ  ( μέσον της ράβδου )  θα έχει δύο κάθετες συνιστώσες ταχύτητας   

  v_M,x = v_B  =  3 m/s   κατά τον άξονα της ράβδου  ( τα διανύσματα   v_B ,  v_A,x ,  v_M,x  είναι ομόρροπα )

  και   v_Μ,y   κάθετη στον άξονα της ράβδου  

 ισχύουν οι σχέσεις :   v_A,y = ω (ΒΑ)  => 4 m/s  =  ω  1 m  =>  ω = 4 rad/s    γωνιακή ταχύτητα 

       v_Μ,y = ω (ΒΜ)  =>  v_Μ,y = 4 rad/s   0, 4 m =>  v_Μ,y = 1,6 m/s

   v_Μ² =   v_M,x²  +  v_Μ,y²  =  3³  +  1,6²  = 11,56  =>  v_M  =  3,4 m/s    

   εφφ =  v_Μ,y / v_M,x = 1,6 / 3 =>  εφφ = 8/15