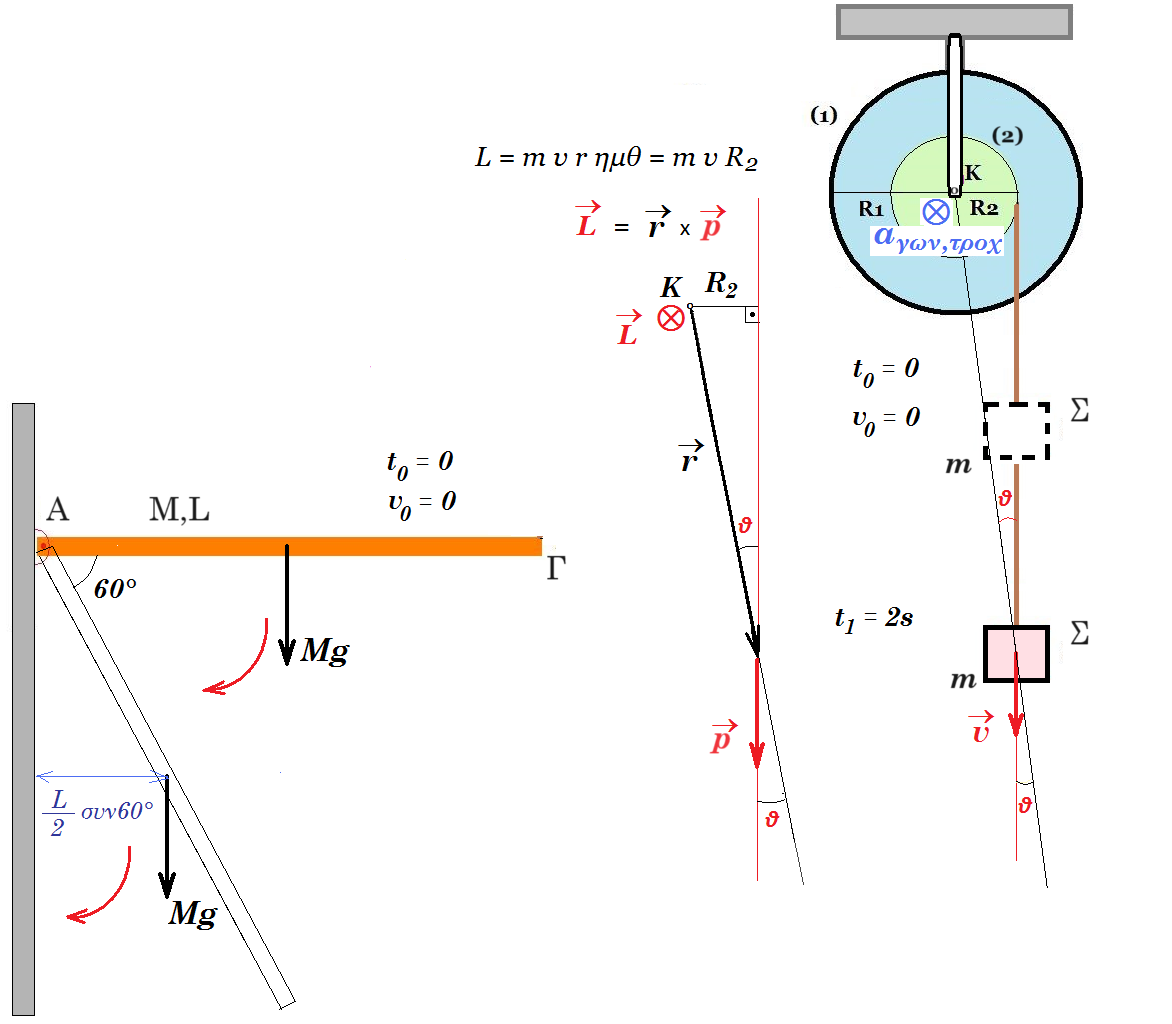
28.  H διπλή τροχαλία μάζας Μτροχ, = 0,5 kg  αποτελείται από δύο ομοαξονικούς κυλίνδρους (1) και (2)  με ακτίνες  R1 = 0,2 m  και R2 = 0,1 m.  Η τροχαλία μπορεί να περιστρέφεται γύρω από ακλόνητο οριζόντιο άξονα x'x που ταυτίζεται με τον άξονα συμμετρίας των δύο κυλίνδρων.  Στην περιφέρεια του κυλίνδρου (1)  έχουμε τυλίξει πολλές φορές αβαρές και μη εκτατό νήμα,  στο ελεύθερο άκρο του οποίου έχουμε συνδέσει το άκρο Γ ράβδου ΑΓ. Το νήμα σχηματίζει γωνία  φ  με την οριζόντιο (ημφ=0,8).  Γύρω από τον κύλινδρο (2)  έχουμε τυλίξει άλλο αβαρές και μη εκτατό νήμα, στο ελεύθερο άκρο του οποίου έχουμε δέσει σώμα Σ μάζας m.  Η ράβδος ΑΓ μάζας Μ = 0,2 kg  και μήκους L = 1,2 m  ισορροπεί οριζόντια.  Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο.

Δ1.  Υπολογίστε τις δυνάμεις που δέχεται η ράβδος  στα άκρα της Α και Γ.

Δ2.  Υπολογίστε τη δύναμη που ασκείται στο κέντρο Κ της τροχαλίας  και  τη μάζα του σώματος Σ.

Tη στιγμή t₀ = 0 κόβουμε το νήμα που συνδέει τη ράβδο με την τροχαλία οπότε η ράβδος αρχίζει να περιστρέφεται χωρίς τριβές γύρω από την άρθρωσή της Α και η διπλή τροχαλία αρχίζει να περιστρέφεται χωρίς τριβές γύρω από τον άξονα x'x. 

Δ3.  Βρείτε την γωνιακή επιτάχυνση της τροχαλίας αν το σώμα Σ κατεβαίνει κατακόρυφα κατά 4m έως τη στιγμήt₁=2s και την στροφορμή του σώματος ως προς το κέντρο Κ της τροχαλίας, την στιγμή t₁.

Δ4.  Aν είναι γνωστό ότι η γωνιακή επιτάχυνση της ράβδου είναι ανάλογη της συνισταμένης των ροπών των δυνάμεων που ασκούνται στη ράβδο ως προς τον άξονα περιστροφής της στο σημείο Α  σύμφωνα με την σχέση Στ_(Α) = Ι α_γων   και αν η γωνιακή επιτάχυνση της ράβδου τη στιγμή t₀ = 0 είναι α_γων = 12,5 r/s² :

   Δ4 α)  βρείτε την επιτάχυνση του άκρου Γ της ράβδου  και  τον συντελεστή αναλογίας Ι 

   Δ4 β)  βρείτε πόση είναι η γωνιακή επιτάχυνση της ράβδου τη στιγμή που σχηματίζει γωνία 60° με την οριζόντιο 

   Δ4 γ)  εκφράστε την γωνιακή επιτάχυνση της ράβδου συναρτήσει της γωνίας  θ  που σχηματίζει η ράβδος με την οριζόντιο καθώς αυτή στρέφεται περί το σημείο Α, μετά το κόψιμο του νήματος

   Δ4 δ)  βρείτε την επιτάχυνση του άκρου Γ της ράβδου όταν αυτή έρχεται σε κατακόρυφη θέση όπου έχει αποκτήσει γωνιακή ταχύτητα ω = 5 r/s.     

Δ1.  ροπές ως προς Α :  M g L/2 = T₁ ημφ L  =>  0,2  10  0,6 = T₁  0,8  1,2  =>  T₁=1,25 Ν   

            ροπές ως προς Γ :  M g L/2  =  F_Α,y L  =>    0,2  10  0,6 = F_Α,y  1,2  =>  F_Α,y = 1 Ν  

   ΣF_x = 0  =>  T₁ συνφ  -  F_A,x  =  0  =>  F_A,x =   T₁ συνφ =  1,25  0,6 =>  F_A,x = 0,75 N 

   F_A²  =  F_A,x²  +  F_A,y²  =  0,75² + 1² =  0,25² ( 3² + 4² ) =  0,25²  5²  =>  F_A = 1,25 N    

    εφθ  =  F_A,y / F_A,x =  1 / 0,75 =>  εφθ = 4/3    

Δ2.  ισορροπία τροχαλίας :  ροπές ως προς Κ :  T₁ R₁ = T₂ R₂  => 1,25 Ν  0,2m = T₂  0,1m  => T₂=2,5N      

ΣF_y = 0  => F_K,y  -  M_τροχ g  - T₁ ημφ  - T₂ = 0  =>  F_K,y = 0,5 10  + 1,25  0,6  + 2,5 => F_K,y=8,25N  

ΣF_x  =  0  =>  F_K,x  -  T₁ συνφ =  0  =>  F_K,x  =  1,25  0,6  =  0,75 N  

F_K²  =  F_K,x²  +  F_K,y²  =  0,75² + 8,25² =  0,75² ( 1² + 11² ) = 0,75²  122  =>  F_K @  8,284 N

ισορροπία Σ :     m g  =  T₂  =>  m 10 =  2,5 =>   m₂  =  0,25 kg  

Δ3.     α_cm  =  α_{γων,τροχ} R₂              

  m g  -  T₂   =  m α_cm =  m α_{γων,τροχ} R₂ =>  2,5  -  T₂  =  0,25 α_{γων,τροχ} 0,1     (1)            I_(K) =  ½ Μ R₁²  = ½  0,5  0,2²  = 0,01 kg m²

    T₂ R₂  = I_(K) α_{γων,τροχ}  =>   T₂ 0,1  = 0,01 α_{γων,τροχ}  =>  T₂ =  0,1 α_{γων,τροχ} (2)  

(1) + (2)  =>  2,5  =  0,125 α_{γων,τροχ}  =>  α_{γων,τροχ} = 20 rad/s²        α_cm = 2 m/s²           T₂ =  0,1 α_{γων,τροχ} = 0,1 20 = 2 N 

 υ_cm = α_cm t = 2 m/s² 2 s = 4 m/s                ω = α_{γων,τροχ}  t = 20  2 = 40 rad/s         h = ½  α_cm  t²  =  ½  2  2²  =  4 m   κατέρχεται  

    κατέρχεται   4 m     h = ½  α_cm  t²  =>  4 m =  ½  α_cm  (2s)²  =>  α_cm =  2 m/s²   

    α_cm  =  α_{γων,τροχ} R₂  =>    α_{γων,τροχ} =  α_cm / R₂ = 2 m/s² / 0,1 m  =>  α_{γων,τροχ} = 20 rad/s²       

  L = m v r ημθ  = m v R₂  =  0,25 kg  4 m/s  0,1 m  =>  L =  0,1 kg m²/s   

η στροφορμή συναρτήσει του χρόνου : L = m v r ημθ = m v R₂ = 0,25 kg  2.t  0,1 m => L(t) = 0,05.t

 ο ρυθμός μεταβολής της στροφορμής :  dL/dt = 0,05 kg m²/s²    

 Στ_(K) = ΣF . R₂  =  ( mg - T₂ ) . R₂ = ( 0,25 kg  10 m/s² - 2 N ) . 0,1 m  =  0,05 kg m²/s²  =  dL/dt 

ο ρυθμός μεταβολής της κινητικής ενέργειας συναρτήσει του χρόνου :

      dK/dt  =  m a v = 0,25 kg  2 m/s²  2.t  = 1.t  

ο ρυθμός μεταβολής του έργου της συνισταμένης δύναμης συναρτήσει του χρόνου :

     dW/dt  = ( mg - T₂ ) v = ( 0,25 kg  10 m/s² - 2 N )  2.t  = 1.t  

ο ρυθμός μεταβολής της δυναμικής ενέργειας βαρύτητας συναρτήσει του χρόνου :  

U = m g h = m g (H - y)     dU/dt = mg (- dy/dt) = - mg v = - 0,25 kg  10 m/s²  2.t = - 5.t

Δ4.     α)     τη στιγμή  t₀=0 :   α_(Γ)  =  α_γων  (ΑΓ)  =  12,5 rad/s²  1,2 m  =  15 m/s²  

         η ράβδος έχει μηδενική ταχύτητα οπότε η κεντρομόλος επιτάχυνση είναι μηδέν

Στ_(Α) = Ι α_γων  => Μg L/2 = I  α_γων =>  2  0,6  =  I  12,5  =>  I = 12 / 125  = 0,096 Nms² 

β)

Στ_(Α) = Ι α_γων  =>  Μg L/2  συν60°  =  I  α_γων  =>  2  0,6  ½  =  24/250  α_γων =>  α_γων = 25/4 rad/s² 

γ)

Στ_(Α) = Ι α_γων  =>  Μg L/2  συνθ  =  I  α_γων  =>  2  0,6  συνθ = 24/250  α_γων =>  α_γων = 25/2 συνθ , 0°£θ£90°

δ)

το άκρο Γ έχει κεντρομόλο επιτάχυνση  α_κ = ω² (ΑΓ) = 5²  1,2 = 30 m/s²  κατακόρυφη προς τα επάνω

  η επιτρόχιος επιτάχυνση   α_{επιτροχ,}  =  α_γων  (ΑΓ)  είναι μηδέν  διότι  θ = 90°  οπότε  συνθ = 0