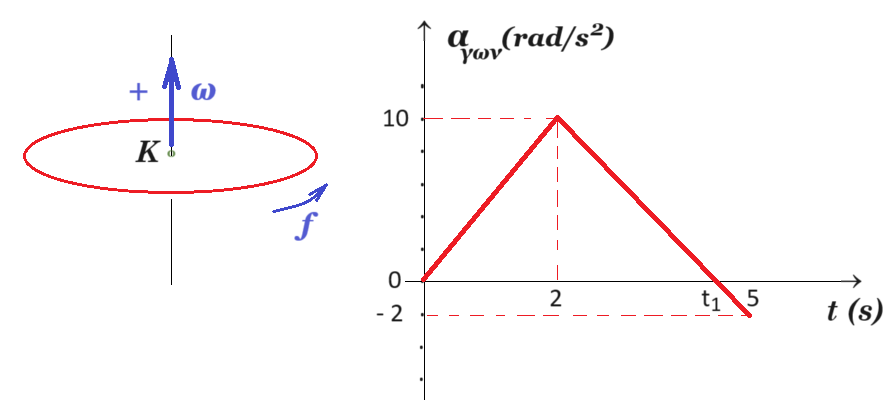
Ένας αρχικά ακίνητος δίσκος αρχίζει την χρονική στιγμή t0=0 να στρέφεται γύρω από σταθερό άξονα. Στο σχήμα φαίνεται η γωνιακή επιτάχυνση του δίσκου σε συνάρτηση με το χρόνο.
Ένας αρχικά ακίνητος δίσκος αρχίζει την χρονική στιγμή t0=0 να στρέφεται γύρω από σταθερό άξονα. Στο σχήμα φαίνεται η γωνιακή επιτάχυνση του δίσκου σε συνάρτηση με το χρόνο.
Η μέγιστη ταχύτητα που θα έχει το σώμα κατά τη διάρκεια της κίνησης από 0-5sec είναι ίση με .....
Γράψτε την εξίσωση της γωνιακής επιτάχυνσης ως προς τον χρόνο καθώς και της γωνιακής ταχύτητας
Να κάνετε τα διαγράμματα ω(t) και θ(t).
μέγιστη ταχύτητα έχει τη στιγμή t1 όπου η γωνιακή ταχύτητα μηδενίζεται και μετά γίνεται αρνητική οπότε μειώνεται η γωνιακή ταχύτητα του δίσκου
όμοια τρίγωνα : ( t1 - 2 ) / ( 5 - t1 ) = 10 / 2 = 5 => t1 - 2 = 5 ( 5 - t1 ) => t1 - 2 = 25 - 5t1 =>
=> 6t1 = 27 => t1 = 27/6 = 4,5 s
από το εμβαδόν του μεγάλου τριγώνου ( πάνω από τον άξονα ) έχουμε : ω = Ε = 10 r/s2 ( 4,5s - 0 ) / 2 = 22,5r/s
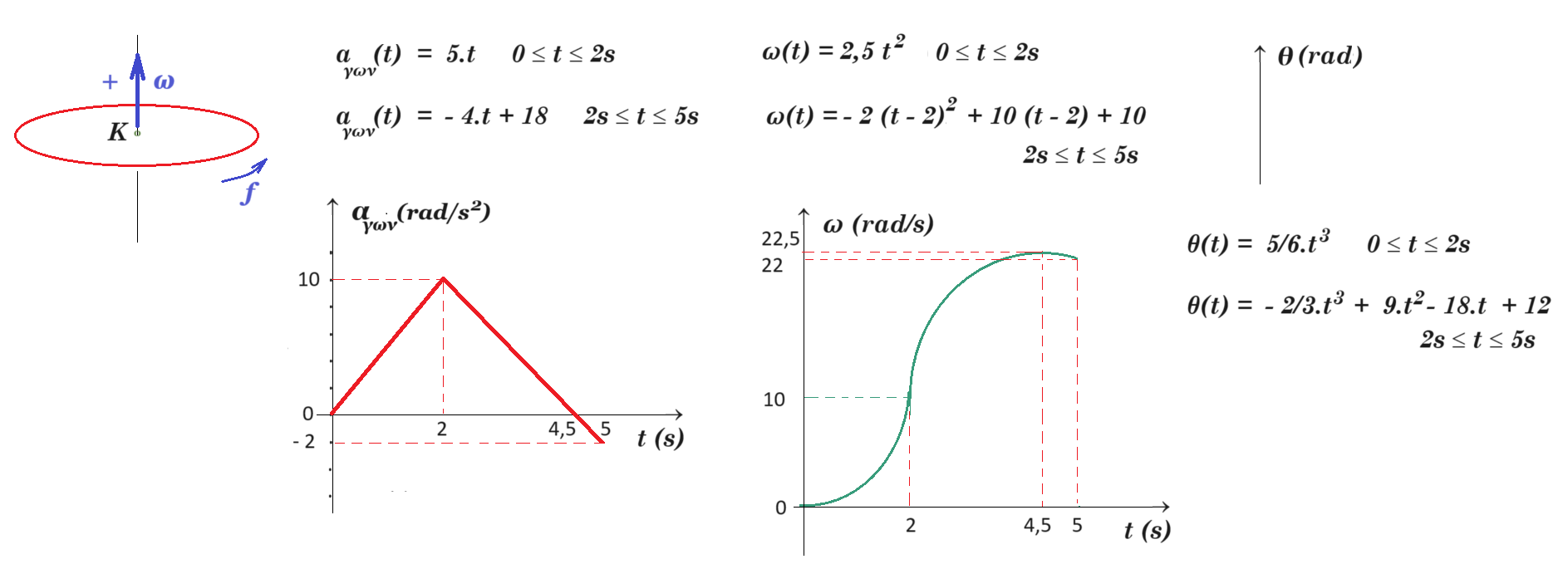
αγων(t) = 5.t 0 £ t £ 2s
αγων = dω/dt => dω = 5.t dt => ω(t) = 2,5 t2 0 £ t £ 2s
ω(t) = 2,5 t2 = dθ/dt => dθ = 2,5.t2 dt => θ(t) = 2,5/3 . t3 = 5/6 . t3 0 £ t £ 2s
θ(2) = 5/6 . 23 = 20/3 rad
αγων = - 4 t + b => 10 = - 4 2 + b => b = 18 αγων(t) = - 4.t + 18 2s £ t £ 5s
αγων = dω/dt => dω = [ - 4 (t - 2) + 10 ] d(t - 2) => ω(t) = - 2 (t - 2)2 + 10 (t - 2) + 10 2s £ t £ 5s
άλλος τρόπος : dω = [ - 4.t + 18 ] dt => ω(t) = - 2.t2 + 18.t + c
ω(2) = 10 = - 2.22 + 18.2 + c => c = 10 + 8 - 36 = - 18 ω(t) = - 2.t2 + 18.t - 18 2s £ t £ 5s
ω(t) = - 2.t2 + 18.t - 18 = dθ/dt => dθ = ( - 2.t2 + 18.t - 18 ) dt => θ(t) = - 2/3.t3 + 9.t2 - 18.t + c
θ(2) = 20/3 = - 2/3 . 23 + 9.22 - 18.2 + c => 20/3 = - 16/3 + 36 - 36 + c => c = 12
τελικά : θ(t) = - 2/3.t3 + 9.t2 - 18.t + 12 2s £ t £ 5s
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
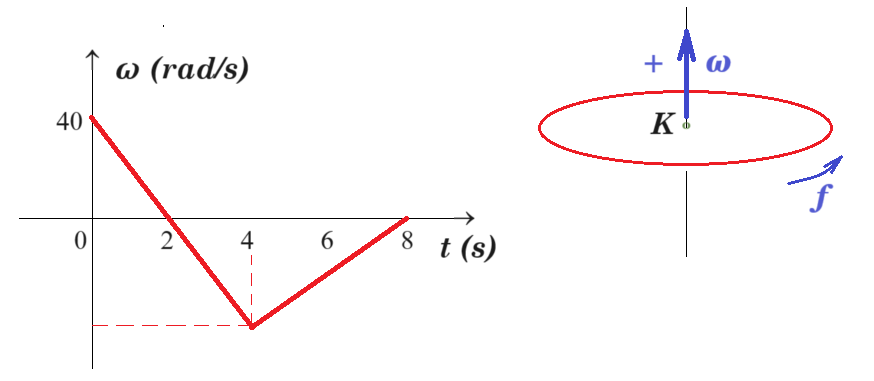
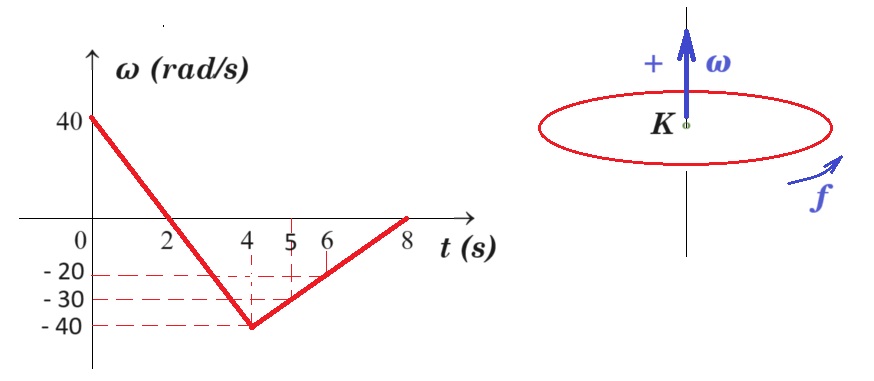
Ο ομογενής δίσκος εκτελεί στροφική κίνηση γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο του Ο και είναι κάθετος στο επίπεδό του. Η ακτίνα του είναι ΟΑ = R = 0,2 m. H γωνιακή ταχύτητά του μεταβάλλεται σε συνάρτηση με το χρόνο, όπως στο σχήμα.
1) Να σχεδιάσετε το διάγραμμα της γωνιακής επιτάχυνσης συναρτήσει του χρόνου.
2) Γράψτε τις εξισώσεις της γωνιακής ταχύτητας συναρτήσει του χρόνου.
3) Να βρεθούν οι γωνιακές ταχύτητες του δίσκου τις χρονικές στιγμές t=1s , t=3s και t=5s
4) Να βρεθούν οι γωνιακές μετατοπίσεις του δίσκου στα χρονικά διαστήματα 0-6s , 2s-5s
5) Να σχεδιάσετε το διάγραμμα της γωνίας περιστροφής σε συνάρτηση με το χρόνο. Η αρχική γωνία είναι μηδέν.
6) Να βρεθεί ο αριθμός των περιστροφών του δίσκου στο χρονικό διάστημα 0-8s.
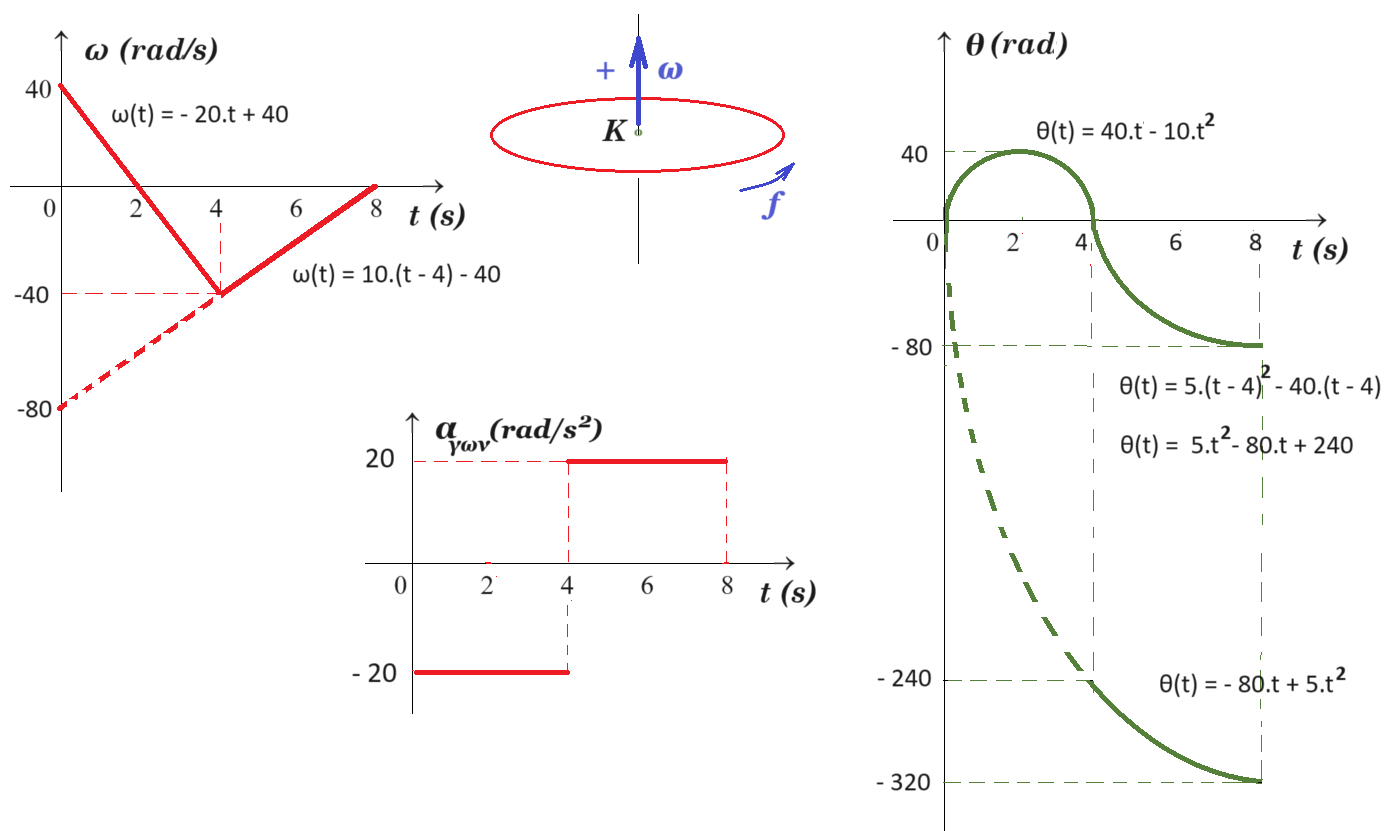
2) Γράψτε τις εξισώσεις της γωνιακής ταχύτητας συναρτήσει του χρόνου.
[ 0 , 4s ] αγων = Δω / Δt = ( 0 - 40 rad/s ) / (2s - 0 ) = - 20 rad/s2 ω(t) = - 20.t + 40
ω(4) = - 20.4 + 40 = - 80 + 40 => ω(4) = - 40 rad/s
[ 4s , 8s ] αγων = Δω / Δt = ( 0 - (- 40 rad/s) ) / (8s - 4s ) = + 10 rad/s2
ω = 10.t + β => - 40 = 10.4 + β => β = - 80 ω(t) = 10.t - 80 ή ω(t) = 10.(t - 4) - 40
3) Να βρεθούν οι γωνιακές ταχύτητες του δίσκου τις χρονικές στιγμές t=1s , t=3s και t=5s
ω(1) = - 20.1 + 40 = - 20 + 40 => ω(1) = + 20 rad/s
ω(3) = - 20.3 + 40 = - 60 + 40 => ω(3) = - 20 rad/s
ω(5) = 10.5 - 80 = 50 - 80 => ω(5) = - 30 rad/s
4) Να βρεθούν οι γωνιακές μετατοπίσεις του δίσκου στα χρονικά διαστήματα 0-6s , 2s-5s
από τα εμβαδά του διαγράμματος ω(t)
στο χρονικό διάστημα [ 0 , 2s ] ο δίσκος "διαγράφει γωνία" + 40 . 2 / 2 = + 40 rad
στο χρονικό διάστημα [ 2s , 4s ] ο δίσκος "διαγράφει γωνία" (- 40) . (4 - 2) / 2 = - 40 rad
στο χρονικό διάστημα [ 4s , 6s ] ο δίσκος "διαγράφει γωνία" [ - 40 + (- 20) ] . (6 - 4) / 2 = - 60 rad
άρα χρονικό διάστημα [ 0 , 6s ] ο δίσκος "διαγράφει γωνία" - 60 rad
στο χρονικό διάστημα [ 2s , 4s ] ο δίσκος "διαγράφει γωνία" (- 40) . (4 - 2) / 2 = - 40 rad
στο χρονικό διάστημα [ 4s , 5s ] ο δίσκος "διαγράφει γωνία" [ - 40 + (- 30) ] . (5 - 4) / 2 = - 35 rad
άρα χρονικό διάστημα [ 2s , 5s ] ο δίσκος "διαγράφει γωνία" - 75 rad
5) Να σχεδιάσετε το διάγραμμα της γωνίας περιστροφής σε συνάρτηση με το χρόνο. Η αρχική γωνία είναι μηδέν.
[ 0 , 4s ] θ = ω0 t + ½ αγων t2 = 40 rad/s t + ½ (- 20 rad/s2) t2 => θ(t) = 40.t - 10.t2
θ(0) = 40.t - 10.t2 = 0 θ(4) = 40.4 - 10.42 = 160 - 160 = 0
[ 4s , 8s ] θ = ω0 t + ½ αγων t2 = - 40 rad/s t + ½ 10 rad/s2 t2 => θ(t) = - 80.t + 5.t2
θ(4) = - 80.4 + 5.42 = - 320 + 80 = - 240 rad θ(8) = - 80.8 + 5.82 = - 640 + 320 = - 320 rad
θ(t) = 5.(t - 4)2 - 40.(t - 4) = 5.t2 + 80 - 40.t - 40.t + 160 => θ(t) = 5.t2 - 80.t + 240
θ(4) = 5.(4 - 4)2 - 40.(4 - 4) = 0
θ(5) = 5.(5 - 4)2 - 40.(5 - 4) = - 35 rad
θ(6) = 5.(6 - 4)2 - 40.(6 - 4) = - 60 rad
θ(8) = 5.(8 - 4)2 - 40.(8 - 4) = - 80 rad
6) Να βρεθεί ο αριθμός των περιστροφών του δίσκου στο χρονικό διάστημα 0-8s.
από τα εμβαδά του διαγράμματος ω(t)
στο χρονικό διάστημα [ 0 , 2s ] ο δίσκος "διαγράφει γωνία" + 40 . 2 / 2 = + 40 rad
στο χρονικό διάστημα [ 2s , 4s ] ο δίσκος "διαγράφει γωνία" (- 40) . (4 - 2) / 2 = - 40 rad και
στο χρονικό διάστημα [ 4s , 8s ] ο δίσκος "διαγράφει γωνία" (- 40) . (8 - 4) / 2 = - 80 rad
συνολικά "διαγράφει γωνία" - 80 rad
στο χρονικό διάστημα [ 0 , 2s ] ο δίσκος εκτελεί Ν1 = 40 / 2π = 20/π στροφές
στο χρονικό διάστημα [ 2s , 4s ] ο δίσκος εκτελεί Ν2 = 40 / 2π = 20/π στροφές και
στο χρονικό διάστημα [ 4s , 8s ] ο δίσκος εκτελεί Ν3 = 80 / 2π = 40/π στροφές
συνολικά εκτελεί 80/π στροφές
