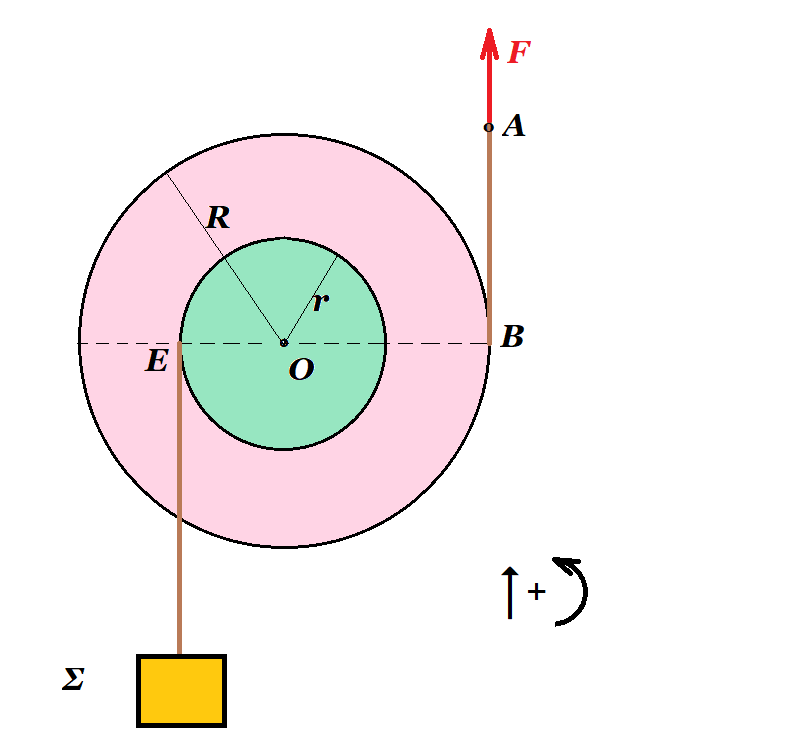

Η διπλή ομογενής τροχαλία του σχήματος, ακτίνας R=0,4m, κινείται κατακόρυφα με την επίδραση μιας κατάλληλης κατακόρυφης δύναμης F, η οποία ασκείται στο άκρο A νήματος, το οποίο έχουμε τυλίξει στο αυλάκι της. Η τροχαλία φέρει ομόκεντρη κυκλική προεξοχή ακτίνας r = 0,2m στην οποία έχουμε τυλίξει ένα δεύτερο νήμα, στο κάτω άκρο του οποίου έχουμε δέσει ένα σώμα Σ. Σε μια στιγμή t1, το άκρο Α του νήματος, στο οποίο ασκείται η δύναμη F, έχει ταχύτητα μέτρου υΑ=1,8m/s, με κατεύθυνση προς τα πάνω, ενώ το σώμα Σ ανεβαίνει επίσης κατακόρυφα, με ταχύτητα μέτρου υΣ=0,6m/s.
Α) Να υπολογιστεί η ταχύτητα του κέντρου Ο της τροχαλίας, καθώς και η γωνιακή ταχύτητα περιστροφής της, γύρω από νοητό οριζόντιο άξονα, ο οποίος διέρχεται από το Ο.
Την παραπάνω στιγμή, το σημείο Α έχει κατακόρυφη επιτάχυνση μέτρου αΑ=3,4m/s2, με φορά προς τα πάνω, ενώ το σώμα Σ, κατακόρυφη επιτάχυνση με φορά προς τα κάτω, μέτρου αΣ=0,2m/s2.
Β) Να υπολογιστούν η επιτάχυνση του κέντρου Ο, καθώς και η γωνιακή επιτάχυνση της τροχαλίας.
Γ) Να βρεθεί ένα σημείο Γ, της οριζόντιας διαμέτρου της τροχαλίας, το οποίο την στιγμή t1 έχει μηδενική κατακόρυφη επιτάχυνση. Στη συνέχεια να υπολογιστεί η ταχύτητα και η επιτάχυνση του σημείου Γ.
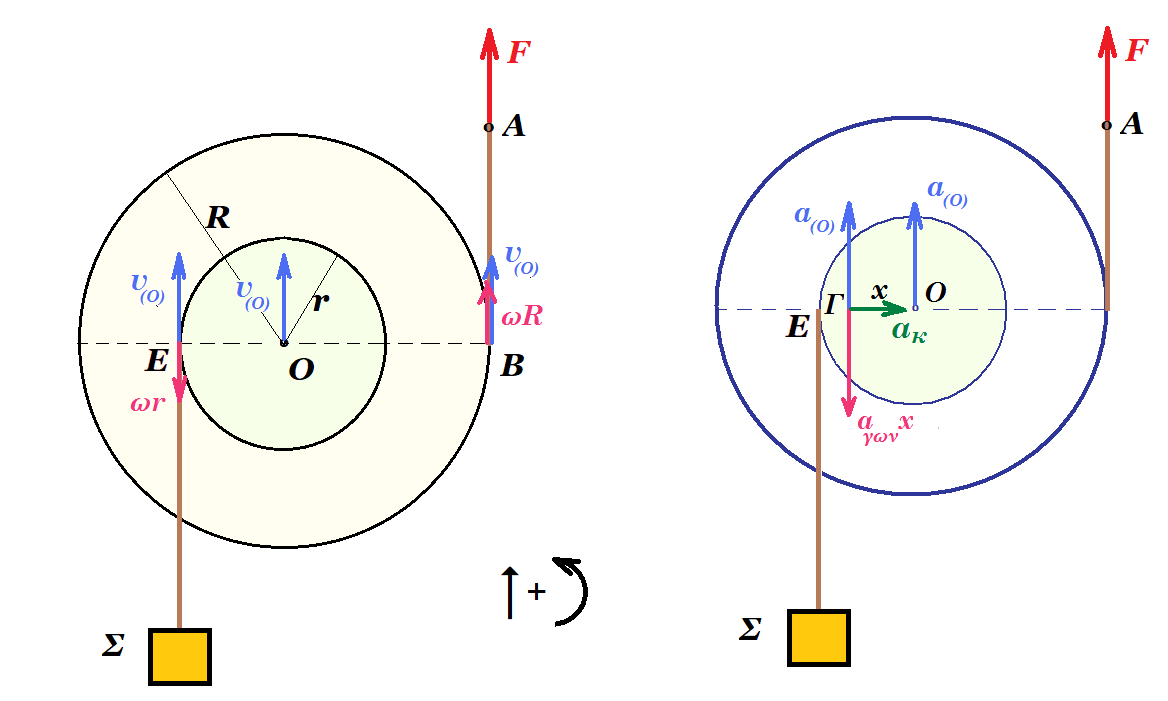
vA = vB = vO + ω R = 1,8 m/s (1) vΣ = vE = vO - ω r = 0,6 m/s (2)
(1) - (2) => ω ( R + r ) = 1,8 - 0,6 => ω ( 0,4 + 0,2 ) = 1,2 => ω = 1,2 / 0,6 = 2 rad/s
(1) => vO + ω R = 1,8 m/s => vO + 2 0,4 = 1,8 => vO = 1,8 - 0,8 = + 1 m/s
aA = aB = aO + αγων R = 3,4 m/s2 (3) αΣ = αE = αO - αγων r = - 0,2 m/s2 (4)
(3) - (4) => αγων ( R + r ) = 3,4 + 0,2 => αγων = 3,6 / 0,6 = 6 rad/s2
(3) => aO + αγων R = 3,4 => aO + 6 0,4 = 3,4 => αΟ = 3,4 - 2,4 = 1 m/s2
aΓ,y = aO + αγων x = 0 => 1 m/s2 + 6 rad/s2 x = 0 => x = - 1/6 m αριστερά του κέντρου Ο
aΓ = aκ = ω2 x = 22 1/6 => aΓ = 2/3 m/s2
vΓ = vO + ω x = 1 m/s + 2 rad/s ( - 1/6 m ) = 1 - 1/3 = 2/3 m/s