ΘΕΜΑ Δ

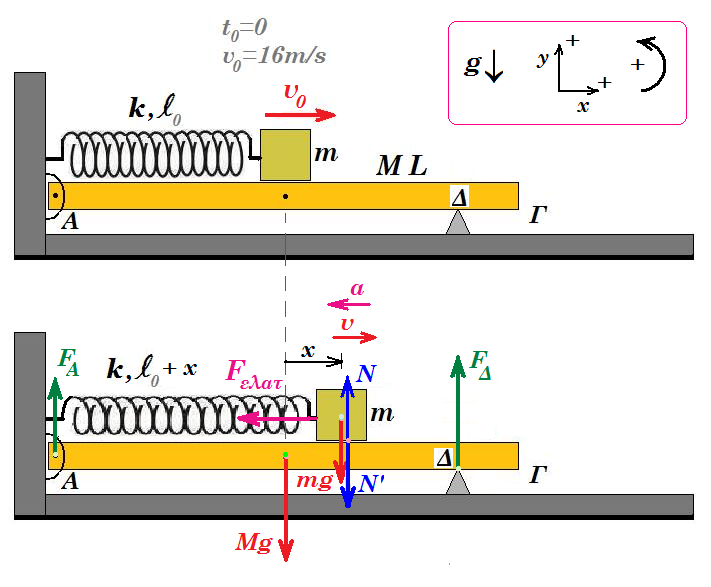
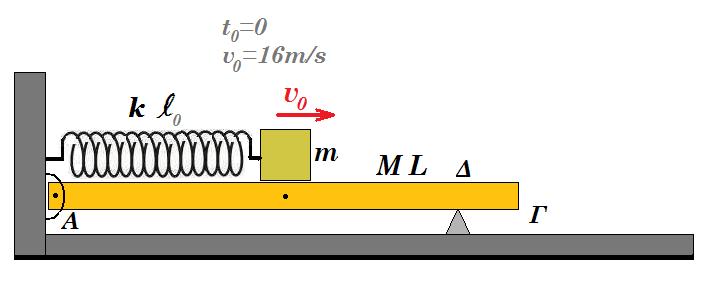
Λεία οριζόντια σανίδα ΑΓ μήκους L = (ΑΓ) = 2 m και μάζας Μ = 3 Kg αρθρώνεται στο άκρο της Α σε κατακόρυφο τοίχο. Σε απόσταση d = 0,4 m από το άκρο Γ, η σανίδα στηρίζεται στο σημείο Δ ώστε να διατηρείται οριζόντια. Ιδανικό αβαρές ελατήριο σταθεράς k = 400 Ν/m συνδέεται με το ένα άκρο του στον τοίχο και το άλλο σε σώμα Σ μάζας m = 1 Kg. Το ελατήριο βρίσκεται στο φυσικό του μήκος, ο άξονάς του είναι οριζόντιος και διέρχεται από το κέντρο μάζας του σώματος Σ. Το κέντρο μάζας του σώματος Σ βρίσκεται σε απόσταση L/2 από τον τοίχο. 
Την στιγμή t₀=0 δίνουμε στο σώμα Σ ταχύτητα υ₀=16m/s με κατεύθυνση προς το άκρο Γ της σανίδας. 

Δ1)   Να υπολογίσετε το πλάτος της απλής αρμονικής ταλάντωσης που θα εκτελέσει το σώμα Σ και γράψτε τις χρονικές εξισώσεις της απομάκρυνσης του σώματος από την θέση ισορροπίας του, της ταχύτητας, της επιτάχυνσης, της δύναμης που ασκεί το ελατήριο στο σώμα,  της κινητικής ενέργειας του σώματος, της δυναμικής ενέργειας της ταλάντωσης , του ρυθμού μεταβολής της κινητικής ενέργειας, του ρυθμού μεταβολής της δυναμικής ενέργειας της ταλάντωσης.   

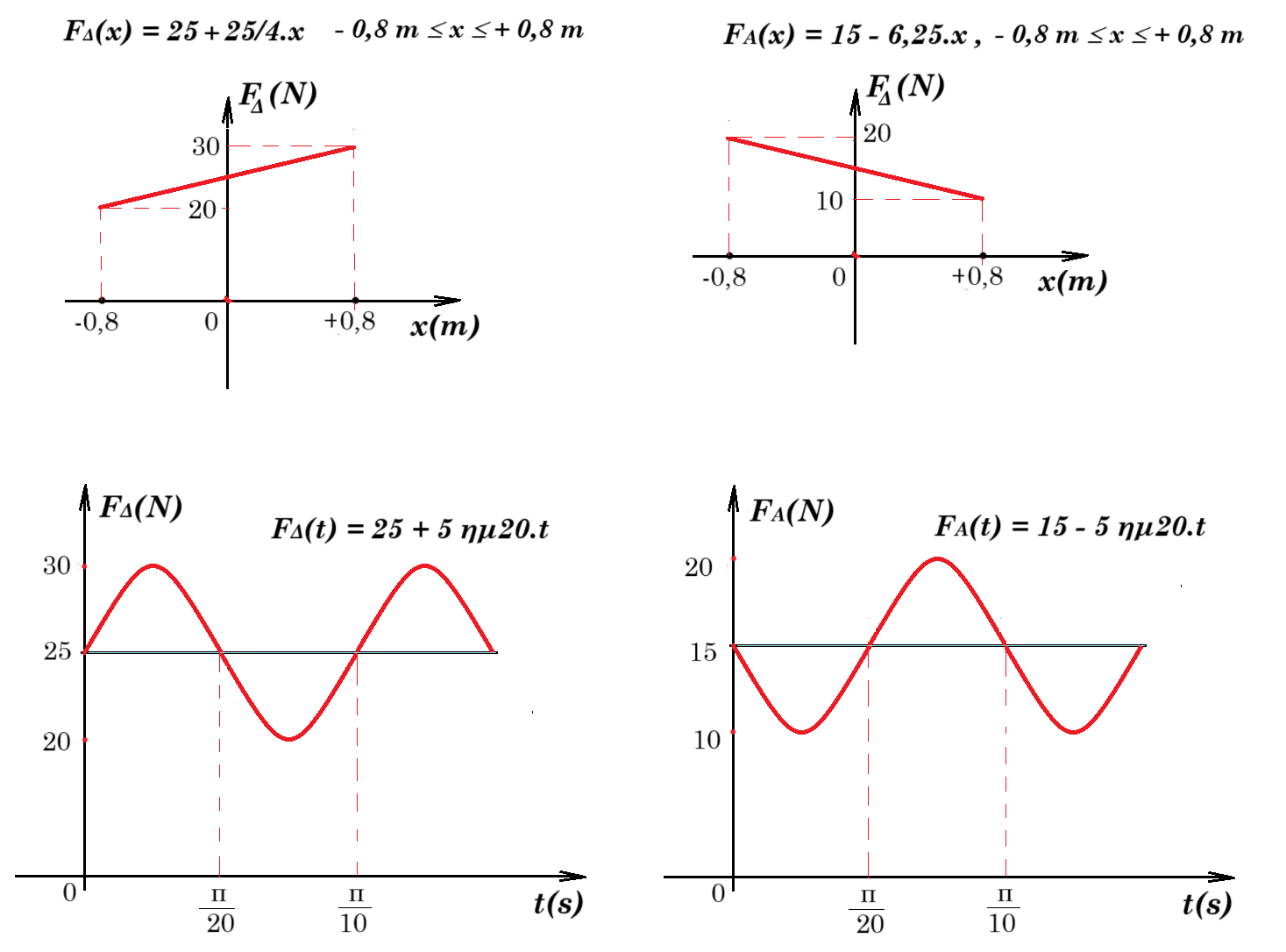
Δ2)   Να εκφράσετε το μέτρο της δύναμης F_Δ που δέχεται η σανίδα στο σημείο Δ από το στήριγμα συναρτήσει του χρόνου και να σχεδιάσετε την αντίστοιχη γραφική παράσταση.  Επίσης να εκφράσετε το μέτρο της δύναμης F_A που δέχεται η σανίδα στο σημείο Α της άρθρωσης  συναρτήσει της απομάκρυνσης του σώματος Σ από την θέση ισορροπίας του και να σχεδιάσετε την αντίστοιχη γραφική παράσταση.

Κατά μήκος της σανίδας από το άκρο Γ κινείται σώμα Σ' ίσης μάζας με ταχύτητα υ' = 6 m/s. Τα δύο σώματα συγκρούονται κεντρικά και ελαστικά, όταν η απομάκρυνση του σώματος Σ είναι x₁, όπου x₁≥ 0. Το σώμα Σ μετά την κρούση ταλαντώνεται με πλάτος Α'=0,5m.

Δ3)   Να βρείτε την απομάκρυνση x₁.
Θεωρούμε θετική τη φορά της απομάκρυνσης προς το Γ και g = 10m/s².

Δ1)

δίνουμε ταχύτητα  υ₀=16m/s  στο σώμα οπότε η αρχική κινητική ενέργεια  ½ m v₀² = ½ 1 kg (16 m/s)² = 128 J   μετατρέπεται σε μέγιστη δυναμική ενέργεια της ταλάντωσης του σώματος 

½ m v₀² =  ½ k A² =>   1 kg (16 m/s)² =   400 N/m  A² =>   A² = (16/20)² =>  A = 0,8 m

ω² = k/m = 400 / 1 =>  ω = 20 r/s            f = ω/2π = 10/π Hz              Τ = π/10 s  

το σώμα εκτελεί Α.Α.Τ.  με πλάτος A = 0,8 m    συχνότητα f = 10/π Hz    αρχική φάση  φ = 0

x(t) = 0,8 ημ20.t                          v(t) = 16 συν20.t                         α(t) = - 320 ημ20.t    

ΣF_x = m a = 1 kg ( - 320 ημ20.t ) = - 320 ημ20.t

F_ελατ = - k x = - 400  0,8 ημ20.t  = - 320 ημ20.t  

U_ελ =  ½ k x² =  ½ 400 x² = 200 x²   - 0,8 m £ x £ + 0,8 m  δυναμική ενέργεια ελατηρίου συναρτήσει της απομάκρυνσης x

U_ελ =  ½ k x² =  ½  400  ( 0,8 ημ20.t )² = 128 ημ²20.t = 128  ( 1 - συν40.t ) / 2  = 64 - 64 συν40.t  δυναμική ενέργεια ελατηρίου,  συναρτήσει του χρόνου

K = ½ m v²  =  ½  1  ( 16 συν20.t ) ²  =  128 συν²20.t  = 128  ( 1 + συν40.t ) / 2  = 64 + 64 συν40.t  κινητική ενέργεια του σώματος κατά την ταλάντωσή του,  συναρτήσει του χρόνου

U =  ½ k x² =  ½  400  ( 0,8 ημ20.t )² = 128 ημ²20.t = 128  ( 1 - συν40.t ) / 2  = 64 - 64 συν40.t  δυναμική ενέργεια ταλάντωσης,  συναρτήσει του χρόνου         χρόνος περιόδου  T' = 2π / 40 = π/20 s

dK/dt = m v a =  1  16 συν20.t   ( - 320 ημ20.t )  =  - 5120 ημ20.t συν20.t =  - 2560 ημ40.t   ρυθμός μεταβολής της κινητικής ενέργειας του σώματος

dU/dt =  k x v  =  400  0,8 ημ20.t  16 συν20.t  = 2560 ημ40.t    ρυθμός μεταβολής της δυναμικής ενέργειας 

Δ2)

η σανίδα ισορροπεί οριζόντια  δέχεται τις δυνάμεις  το βάρος της Μg,  την αντίδραση F_Δ στο σημείο Δ από το στήριγμα, την αντίδραση Ν' από το σώμα που ταλαντώνεται, η οποία έχει μέτρο ίσο με το βάρος του σώματος 

ροπές ως προς Α :  Στ_(Α) = 0  =>  - Μg L/2  -  mg (L/2 + x)  + F_Δ (L - d)  =  0  => 

     =>  - 30 N 1m  -   10 N ( 1m + x )  + F_Δ 1,6m  =  0     (1)

     (1)  =>  - 30  - 10 - 10x  + F_Δ 1,6  =  0   =>  F_Δ(x) = 25 + 25/4.x    -0,8m £  x £ +0,8m

ή   (1)  =>  - 30 N 1m  -  10 N ( 1m + 0,8 ημ20.t )  + F_Δ 1,6m  =  0  => 

=> - 30  - 10  - 8 ημ20.t  + F_Δ 1,6  = 0  => F_Δ = 40/1,6 + 8/1,6 ημ20.t  =>  F_Δ(t) = 25 + 5 ημ20.t 

ροπές ως προς Δ :  Στ_(Δ) = 0  =>  + Μg (L/2 - d)  +  mg (L/2 - d - x)  +  F_A (L - d)  =  0  => 

=> - 30N 0,6m  - 10N (0,6m - x)  + F_A 1,6m  = 0  => - 18 - 6 + 10.x + F_A 1,6  => F_A(x) = 15 - 6,25.x , -0,8m £  x £ +0,8m

ροπές ως προς Δ :  Στ_(Δ) = 0  =>  + Μg (L/2 - d)  +  mg (L/2 - d - x)  +  F_A (L - d)  =  0  => 

     =>  - 30 N 0,6m  -   10 N ( 0,6m - 0,8 ημ20.t )  +  F_A  1,6m  =  0  => 

  => - 18 - 6 + 8 ημ20.t  + F_A  1,6  =  0  =>F_A = 24/1,6 - 8/1,6 ημ20.t  =>  F_A(t) = 15 - 5 ημ20.t       

Δ3)

τα δύο σώματα έχουν ίσες μάζες οπότε κατά την κεντρική ελαστική κρούση ανταλλάσσουν ταχύτητες

      ½ k (A')²  =  ½ k x₁²  +  ½ m (υ')²    =>   ½  400  0,5²  =  ½ 400  x₁²  +  ½ 1 6²  => 

  =>   100 = 400 x₁²  + 36   =>    x₁²  =  64/400  =  0,16  =>  x₁ = 0,4 m