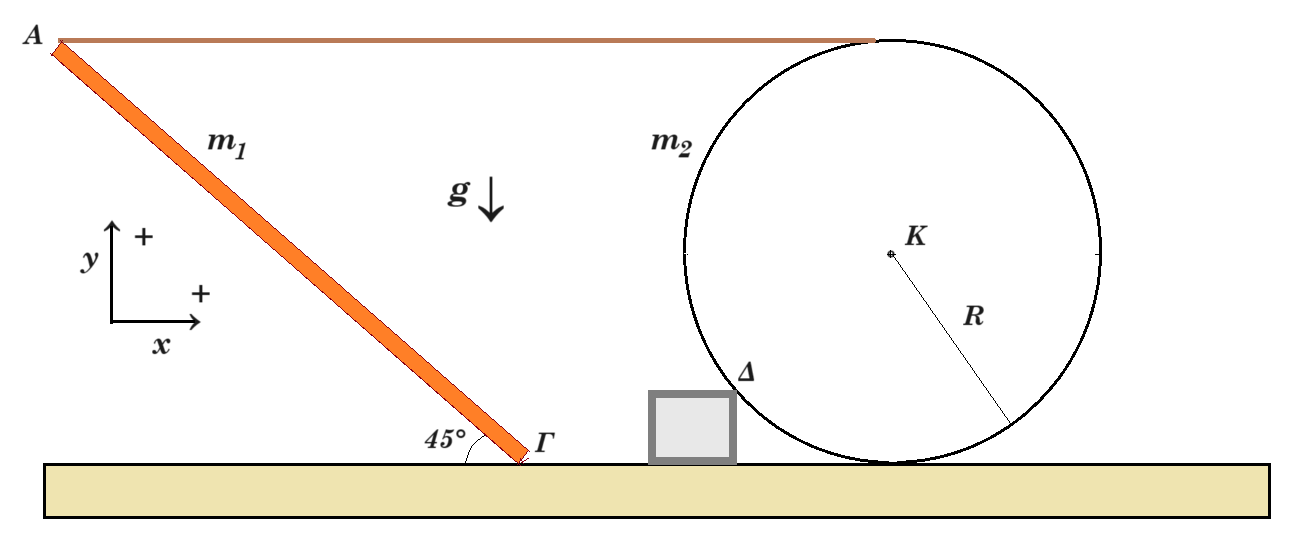
Ομογενής ράβδος (ΑΓ) μήκους ℓ και μάζας Μ₁ ισορροπεί οριακά ακίνητη πάνω σε τραχύ επίπεδο με την διεύθυνση της να σχηματίζει γωνία φ = 45° με το οριζόντιο επίπεδο. Στο άκρο της Α είναι δεμένο οριζόντιο αβαρές και μη εκτατό νήμα το άλλο άκρο του οποίου είναι δεμένο στο ανώτερο σημείο ομογενούς δίσκου ακτίνας R και μάζας Μ₂. Η απόσταση του νήματος από το οριζόντιο επίπεδο είναι d = 2R. Ο δίσκος ισορροπεί ακίνητος και οριακά δεν υπερπηδά το ακλόνητο εμπόδιο ύψους h (h = 0,4R) με το οποίο είναι σε επαφή όπως φαίνεται στο παρακάτω σχήμα. Να υπολογίσετε:

(α)  την τιμή του συντελεστή στατικής τριβής μεταξύ ράβδου και επιπέδου

(β)  την τιμή της μάζας Μ₂ σε σχέση με την μάζα Μ₁

(γ)  το μέτρο της δύναμης που δέχεται ο δίσκος από το εμπόδιο σε σχέση με το μέτρο του βάρους του (w₂).